Code
import numpy as np
import matplotlib.pyplot as pltHomework #3 – Getting Started Guide
1 Covariance and Linear Estimation
1.1 Understanding Covariance Matrices
The covariance matrix captures the relationship between random variables. For two variables:
\(\mathbf{K} = \begin{bmatrix} \text{Var}(X) & \text{Cov}(X,Y) \\ \text{Cov}(X,Y) & \text{Var}(Y) \end{bmatrix}\)
Consider this visualization:
Code
def plot_covariance_example(rho, n_points=1000):
"""Demonstrate covariance with correlation rho"""
mean = [0, 0]
cov = [[1, rho], [rho, 1]]
data = np.random.multivariate_normal(mean, cov, n_points)
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))
# Scatter plot
ax1.scatter(data[:, 0], data[:, 1], alpha=0.5)
ax1.set_title(f'Sample Data (ρ = {rho})')
ax1.set_xlabel('X')
ax1.set_ylabel('Y')
ax1.grid(True)
ax1.axis('equal')
# Density visualization
H, xedges, yedges = np.histogram2d(data[:, 0], data[:, 1], bins=20)
ax2.imshow(H.T, origin='lower', extent=[xedges[0], xedges[-1],
yedges[0], yedges[-1]])
ax2.set_title('Density Heatmap')
ax2.set_xlabel('X')
ax2.set_ylabel('Y')
plt.tight_layout()
plt.show()
# Show different correlation structures
for rho in [-0.8, 0, 0.8]:
plot_covariance_example(rho)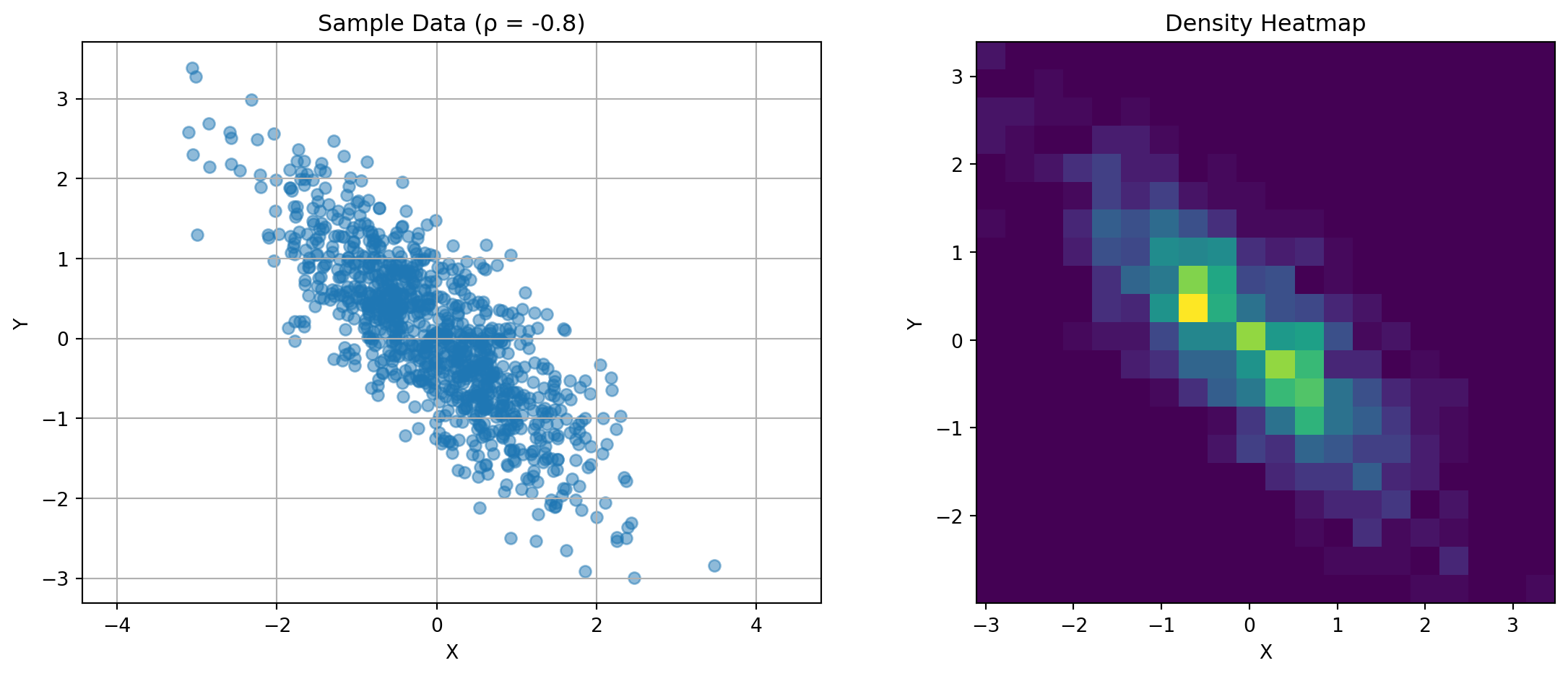
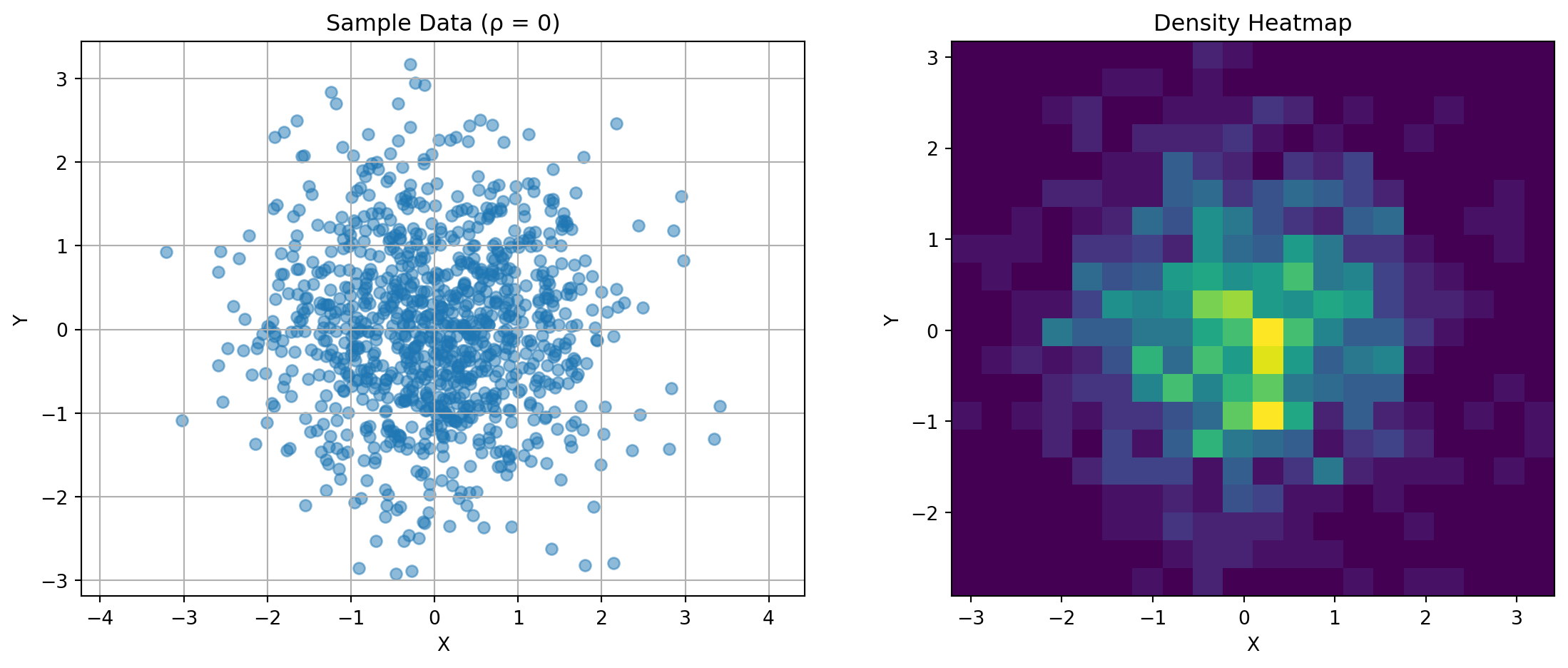
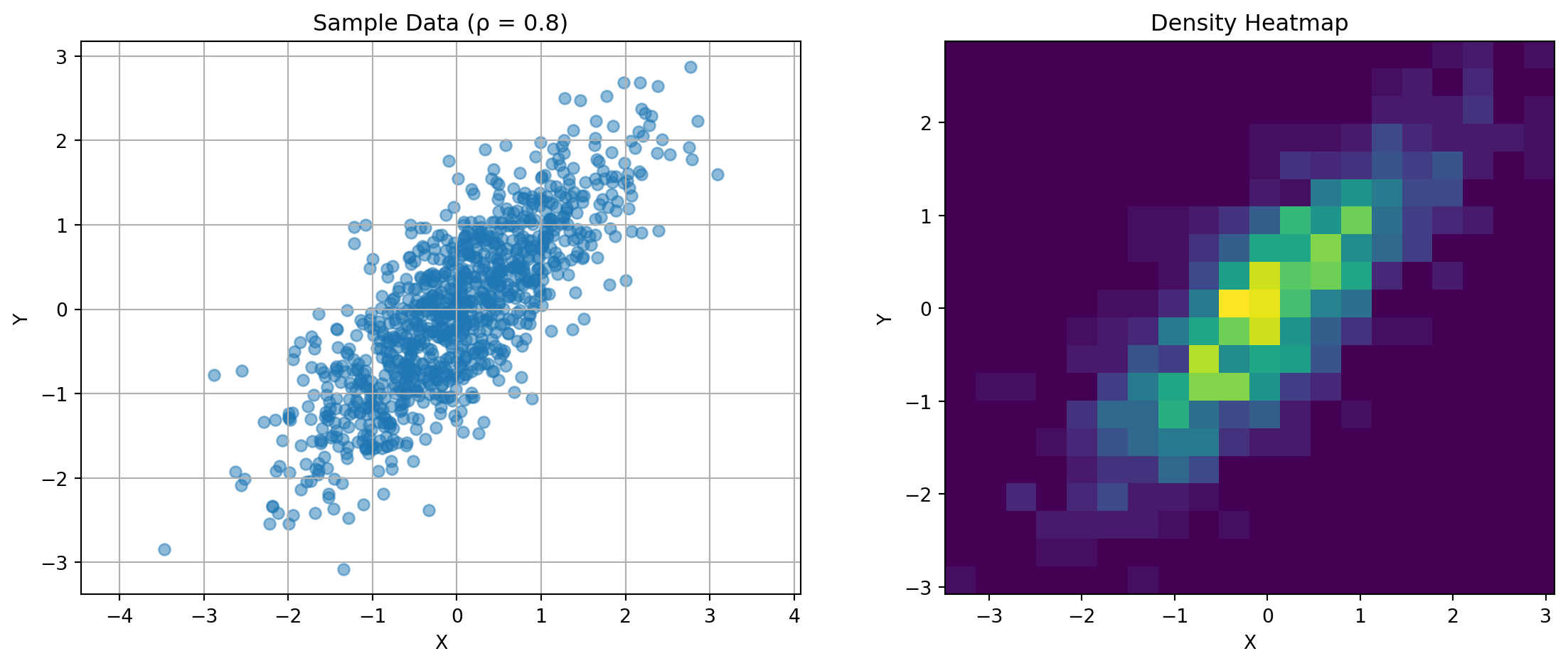
Key observations:
- Diagonal elements represent individual variances
- Off-diagonal elements capture linear relationships
- Symmetric by definition
- Positive semi-definite (all eigenvalues ≥ 0)
1.2 Eigenanalysis of Covariance
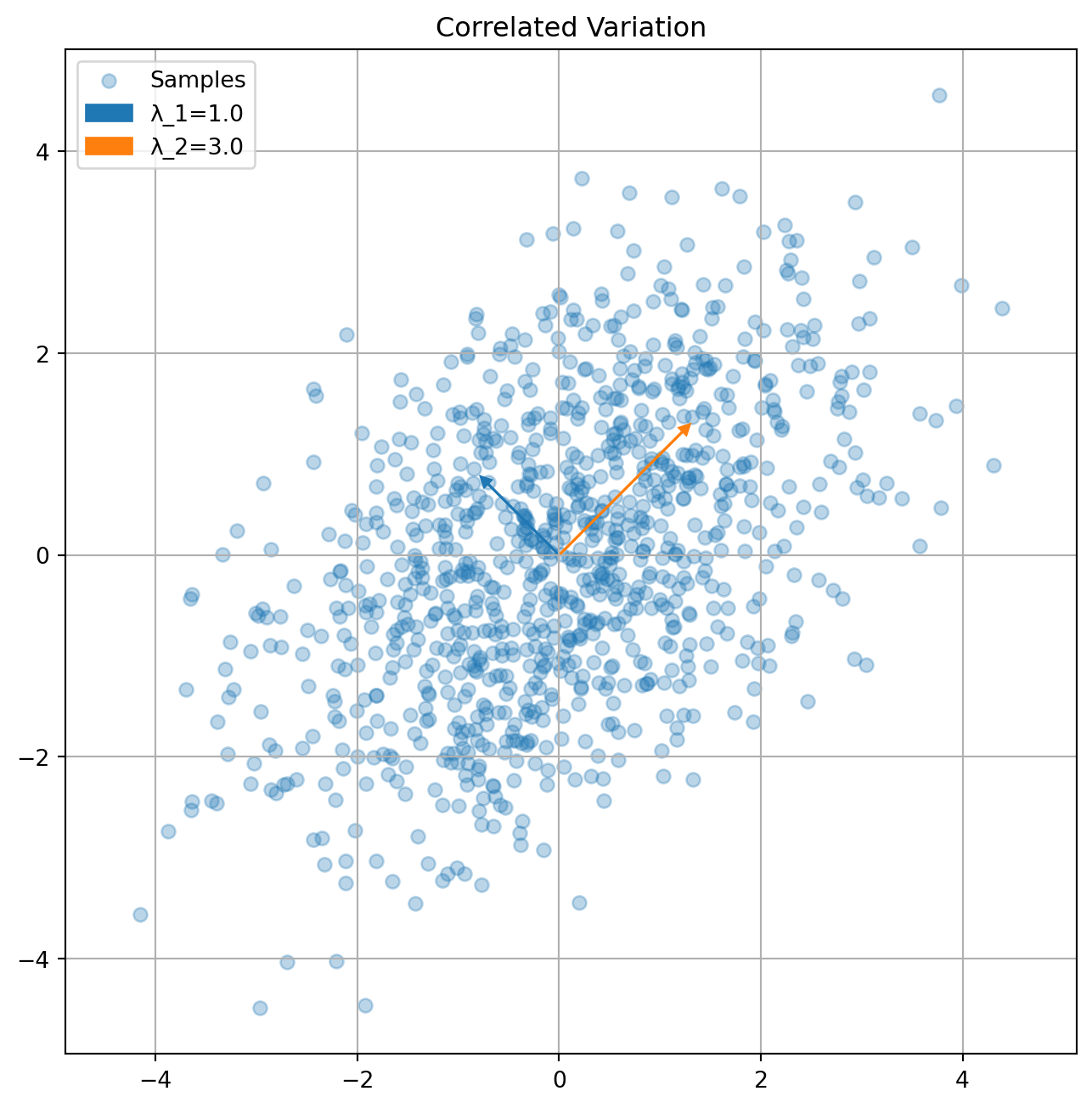
The eigendecomposition reveals principal directions of variation:
Code
def plot_covariance_directions(cov, title="Covariance Directions"):
"""Visualize principal directions of covariance matrix"""
eigenvals, eigenvecs = np.linalg.eigh(cov)
n_points = 1000
data = np.random.multivariate_normal([0,0], cov, n_points)
plt.figure(figsize=(8,8))
plt.scatter(data[:,0], data[:,1], alpha=0.3, label='Samples')
# Plot eigenvectors scaled by eigenvalues
for i in range(2):
vec = eigenvecs[:,i] * np.sqrt(eigenvals[i])
plt.arrow(0, 0, vec[0], vec[1], color=f'C{i}',
head_width=0.1, head_length=0.1,
label=f'λ_{i+1}={eigenvals[i]:.1f}')
plt.axis('equal')
plt.grid(True)
plt.legend()
plt.title(title)
plt.show()
# Example covariance matrices
K1 = np.array([[2, 0], [0, 1]]) # Axis-aligned
K2 = np.array([[2, 1], [1, 2]]) # Correlated
plot_covariance_directions(K1, "Axis-Aligned Variation")
plot_covariance_directions(K2, "Correlated Variation")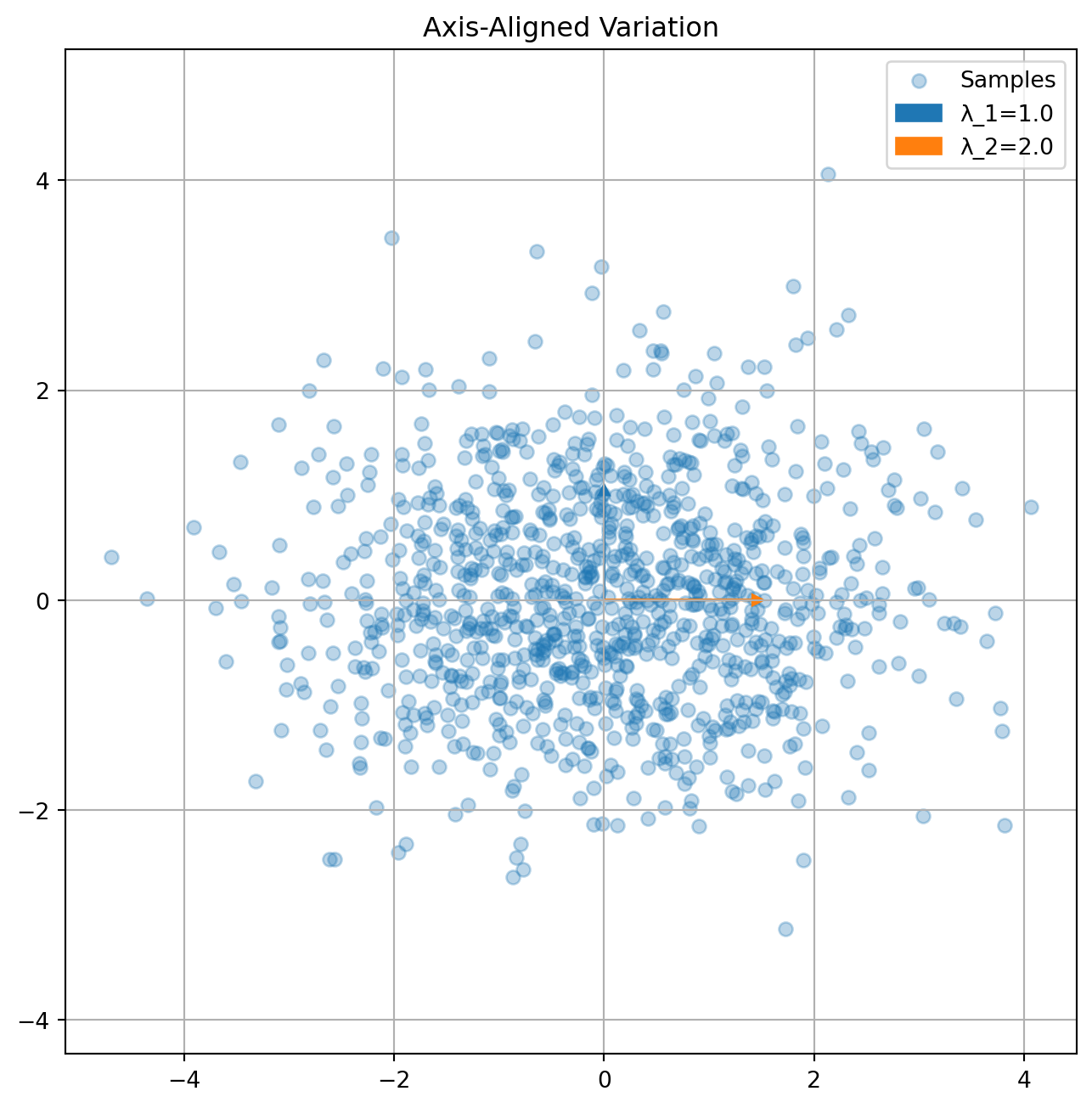
1.3 Linear MMSE Estimation
Linear estimation finds the best linear approximation:
Code
n_points = 200
x = np.linspace(-3, 3, n_points)
y_linear = 2*x + np.random.normal(0, 0.5, n_points)
y_nonlinear = x**2 + np.random.normal(0, 0.5, n_points)
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12,5))
ax1.scatter(x, y_linear, alpha=0.5)
ax1.plot(x, 2*x, 'r-', label='True Relationship')
ax1.set_title('Linear Relationship')
ax1.grid(True)
ax1.legend()
ax2.scatter(x, y_nonlinear, alpha=0.5)
ax2.plot(x, x**2, 'r-', label='True Relationship')
ax2.set_title('Nonlinear Relationship')
ax2.grid(True)
ax2.legend()
plt.show()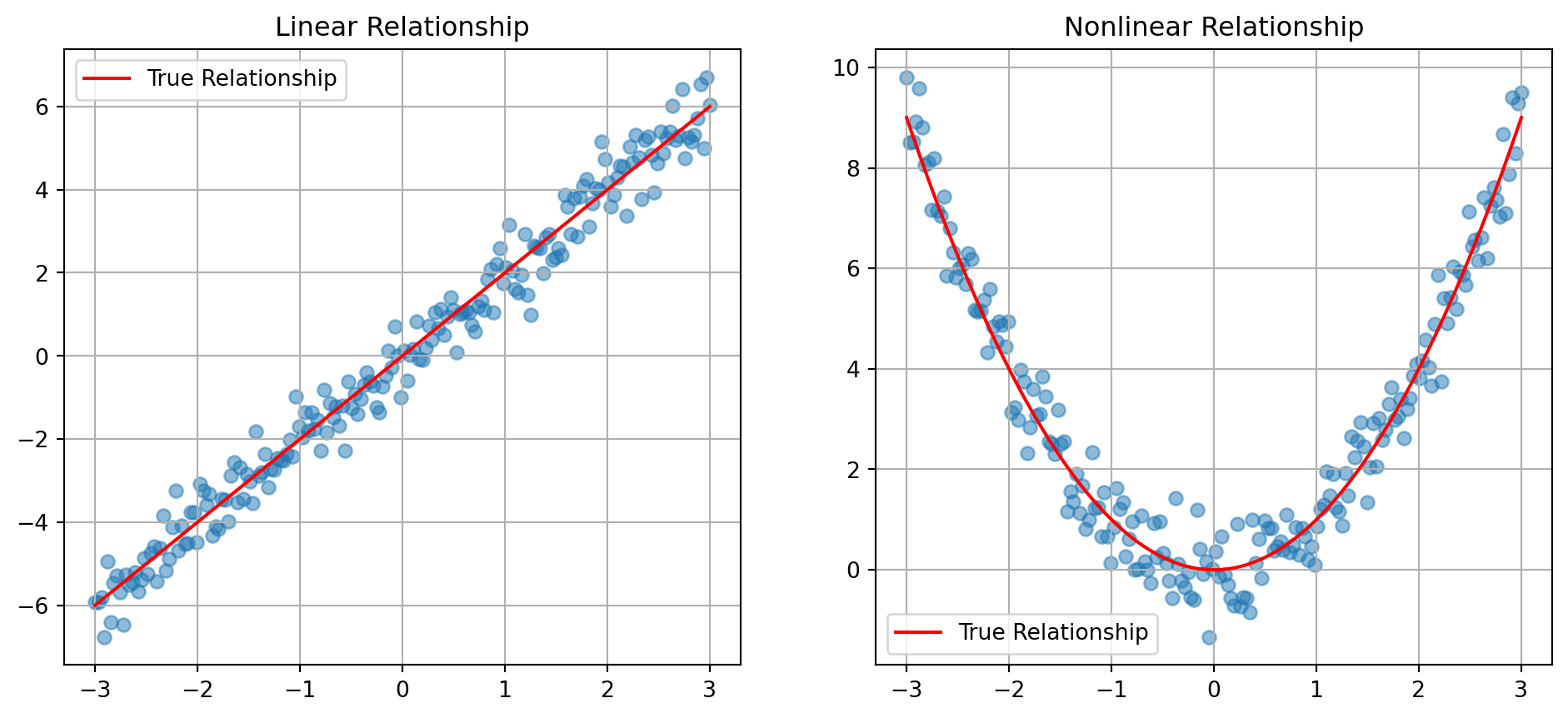
2 Principal Component Analysis
Code
import numpy as np
import matplotlib.pyplot as plt2.1 Geometric Interpretation
PCA finds orthogonal directions of maximum variance:
Code
def generate_banana_data(n_points=1000):
"""Generate curved 2D distribution"""
t = np.linspace(0, 2*np.pi, n_points)
x = 2*np.cos(t) + np.random.normal(0, 0.2, n_points)
y = np.sin(2*t) + np.random.normal(0, 0.2, n_points)
return np.column_stack([x, y])
data = generate_banana_data()
mean = np.mean(data, axis=0)
centered = data - mean
cov = np.cov(centered.T)
eigenvals, eigenvecs = np.linalg.eigh(cov)
plt.figure(figsize=(8,8))
plt.scatter(data[:,0], data[:,1], alpha=0.5, color='gray', label='Data Points')
colors = ['red', 'green']
for i in range(2):
vec = eigenvecs[:,i] * np.sqrt(eigenvals[i])
plt.arrow(mean[0], mean[1], vec[0], vec[1],
color=colors[i], head_width=0.1, linewidth=2,
label=f'PC{i+1} (var={eigenvals[i]:.2f})')
plt.axis('equal')
plt.grid(True)
plt.legend()
plt.title('Principal Components of Curved Distribution')
plt.show()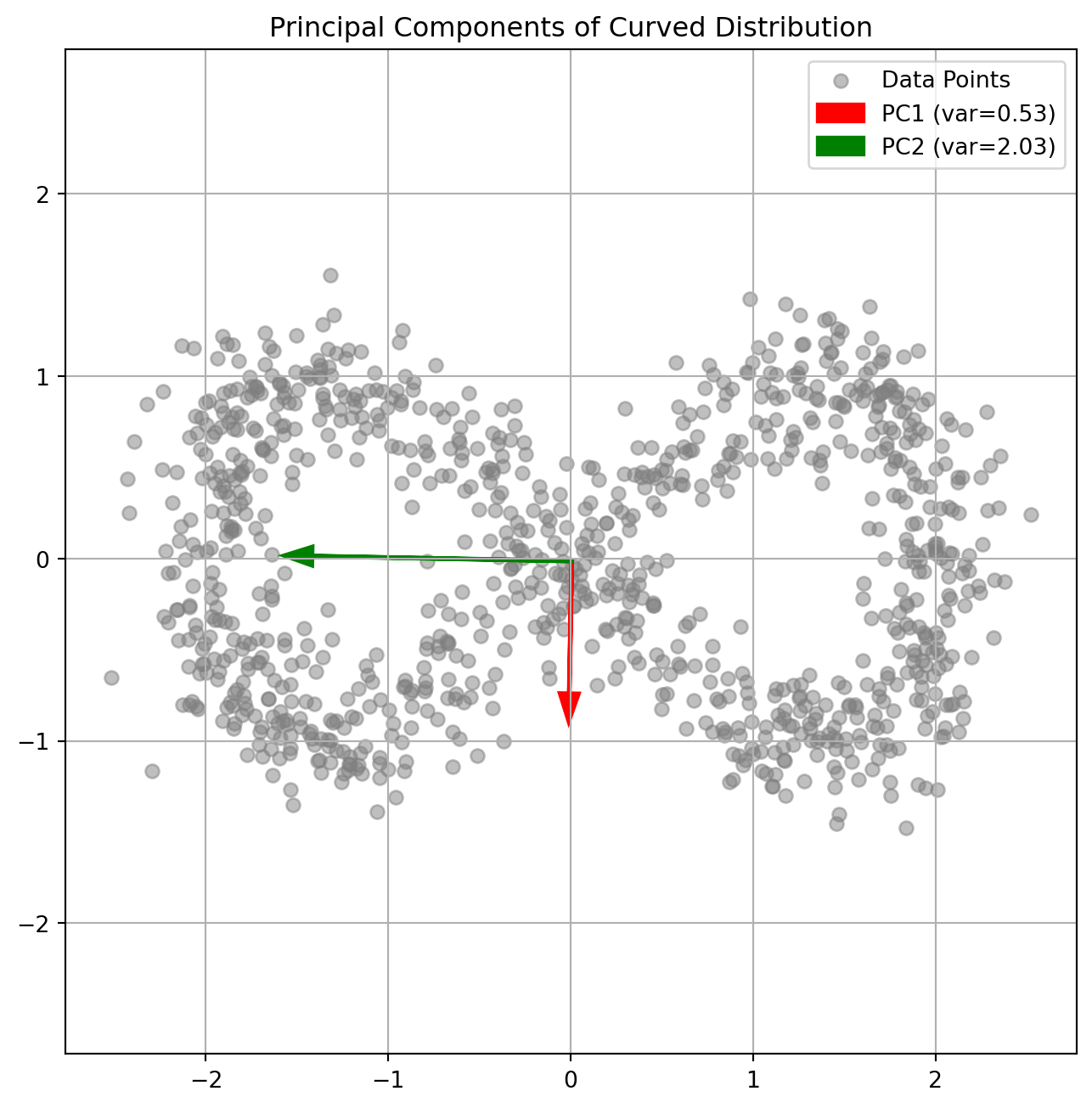
2.2 Dimensionality Reduction
PCA allows optimal linear dimensionality reduction:
Code
# 3D example
from mpl_toolkits.mplot3d import Axes3D
def plot_3d_reduction():
# Generate 3D data primarily in 2D plane
n_points = 500
X = np.random.normal(0, 1, n_points)
Y = 0.3*X + np.random.normal(0, 0.1, n_points)
Z = 0.2*X + 0.1*Y + np.random.normal(0, 0.1, n_points)
data = np.column_stack([X, Y, Z])
# PCA
mean = np.mean(data, axis=0)
centered = data - mean
cov = np.cov(centered.T)
eigenvals, eigenvecs = np.linalg.eigh(cov)
# Plot
fig = plt.figure(figsize=(12,5))
ax1 = fig.add_subplot(121, projection='3d')
ax1.scatter(X, Y, Z, alpha=0.5)
ax1.set_title('Original Data')
# Project onto first two PCs
proj = centered @ eigenvecs[:,-2:]
ax2 = fig.add_subplot(122)
ax2.scatter(proj[:,0], proj[:,1], alpha=0.5)
ax2.set_title('2D Projection')
ax2.grid(True)
plt.show()
print("Eigenvalues (variance explained):")
print(eigenvals)
plot_3d_reduction()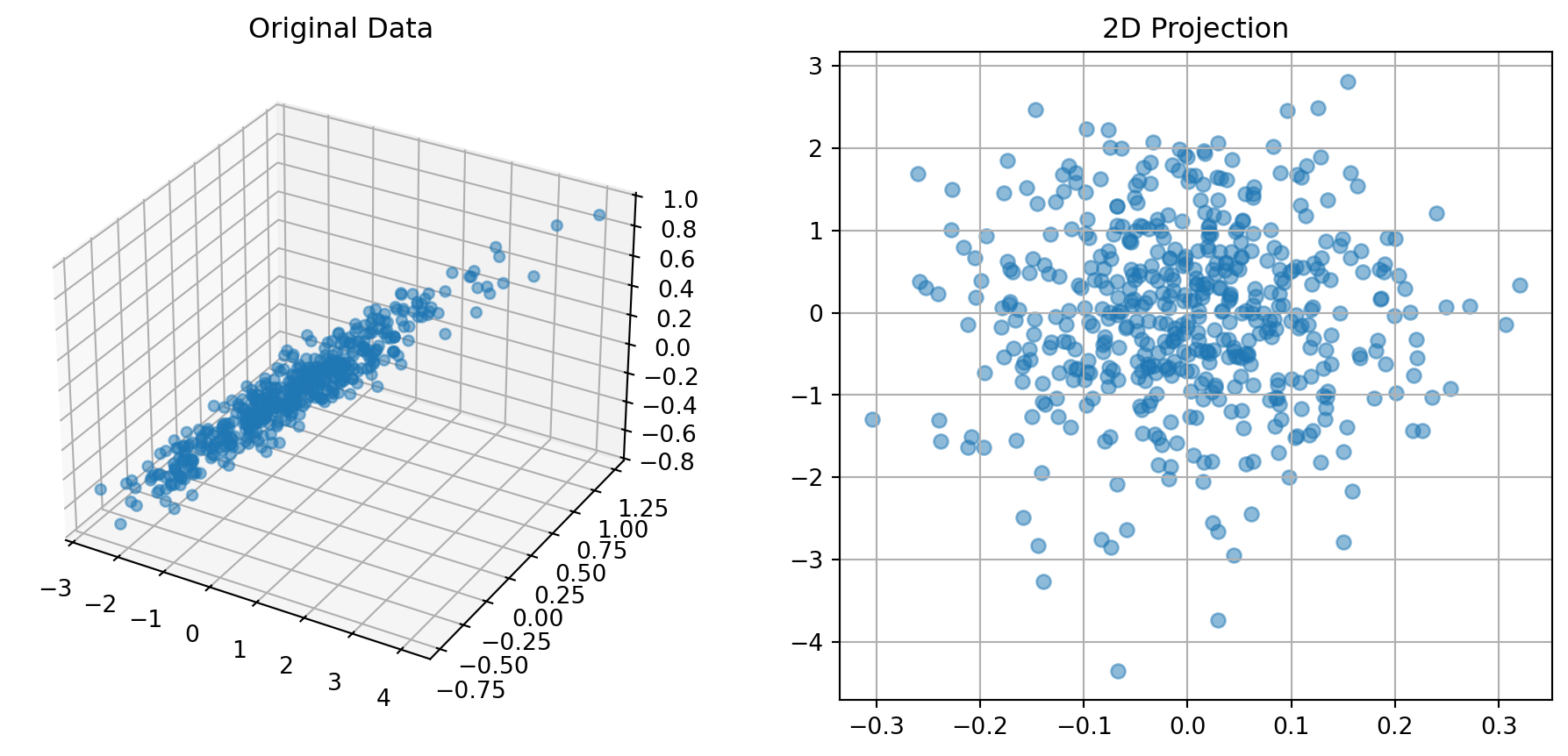
Eigenvalues (variance explained):
[0.00929629 0.0111048 1.17121035]3 Polynomial Regression
Code
import numpy as np
import matplotlib.pyplot as plt3.1 Design Matrix Construction
The design matrix structure affects numerical stability:
Code
def plot_design_matrix_condition(max_degree=5):
"""Show condition number growth"""
x = np.linspace(-1, 1, 100)
conditions = []
for degree in range(1, max_degree+1):
# Construct design matrix
X = np.vstack([x**p for p in range(degree+1)]).T
# Compute condition number
cond = np.linalg.cond(X.T @ X)
conditions.append(cond)
plt.figure(figsize=(8,4))
plt.semilogy(range(1, max_degree+1), conditions, 'o-')
plt.grid(True)
plt.xlabel('Polynomial Degree')
plt.ylabel('Condition Number')
plt.title('Numerical Stability vs Polynomial Degree')
plt.show()
plot_design_matrix_condition()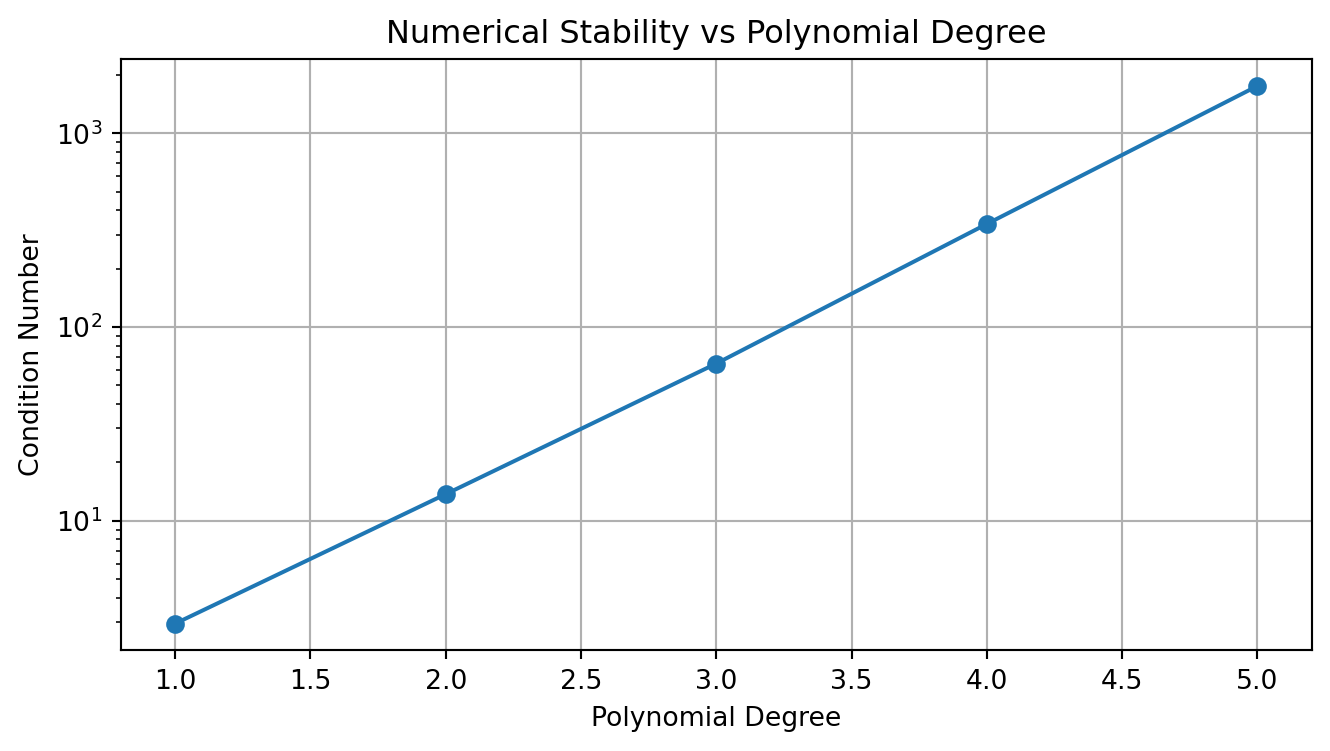
3.2 Regularization Effects
L2 regularization stabilizes the solution:
Code
# Generate noisy polynomial data
x = np.linspace(-1, 1, 50)
y_true = 1 - 2*x + 0.5*x**2
y = y_true + np.random.normal(0, 0.1, len(x))
# Fit polynomials with different regularization
def fit_polynomial(x, y, degree=2, alpha=0.0):
X = np.vstack([x**p for p in range(degree+1)]).T
XtX = X.T @ X
if alpha > 0:
XtX += alpha * np.eye(XtX.shape[0])
w = np.linalg.solve(XtX, X.T @ y)
return w
plt.figure(figsize=(10,5))
x_fine = np.linspace(-1, 1, 200)
X_fine = np.vstack([x_fine**p for p in range(5+1)]).T
for alpha in [0, 0.1, 1.0]:
w = fit_polynomial(x, y, degree=5, alpha=alpha)
y_pred = X_fine @ w
plt.plot(x_fine, y_pred, label=f'α={alpha}')
plt.scatter(x, y, color='black', alpha=0.5, label='Data')
plt.plot(x_fine, 1 - 2*x_fine + 0.5*x_fine**2, 'k--',
label='True Function')
plt.grid(True)
plt.legend()
plt.title('Effect of L2 Regularization')
plt.show()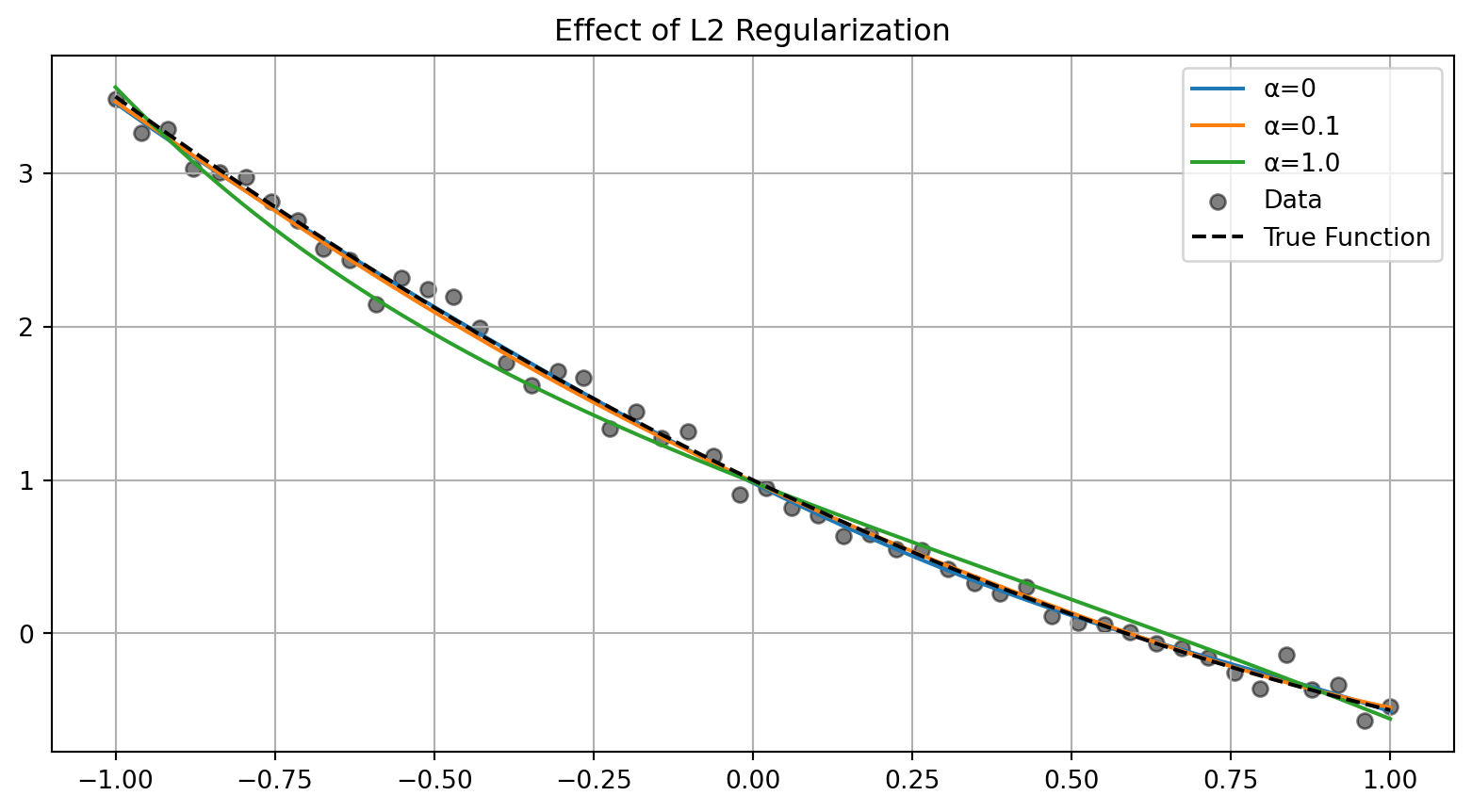
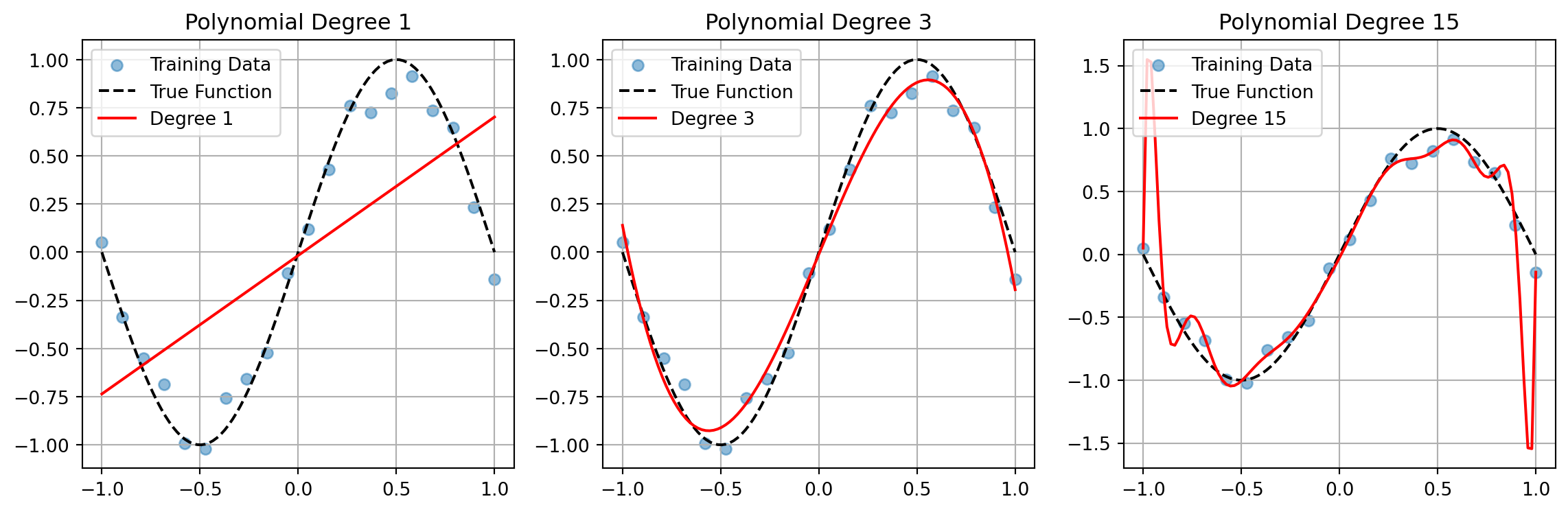
3.3 Bias-Variance Tradeoff
Model complexity affects both bias and variance:
Code
def plot_complexity_tradeoff():
# Generate training and test data
np.random.seed(42)
x_train = np.linspace(-1, 1, 20)
y_train = np.sin(np.pi*x_train) + np.random.normal(0, 0.1, len(x_train))
x_test = np.linspace(-1, 1, 100)
y_test = np.sin(np.pi*x_test)
# Fit polynomials of different degrees
degrees = [1, 3, 15]
plt.figure(figsize=(12,4))
for i, degree in enumerate(degrees):
X_train = np.vstack([x_train**p for p in range(degree+1)]).T
w = np.linalg.solve(X_train.T @ X_train, X_train.T @ y_train)
X_test = np.vstack([x_test**p for p in range(degree+1)]).T
y_pred = X_test @ w
plt.subplot(1,3,i+1)
plt.scatter(x_train, y_train, alpha=0.5, label='Training Data')
plt.plot(x_test, y_test, 'k--', label='True Function')
plt.plot(x_test, y_pred, 'r-', label=f'Degree {degree}')
plt.grid(True)
plt.legend()
plt.title(f'Polynomial Degree {degree}')
plt.tight_layout()
plt.show()
plot_complexity_tradeoff()