Computational Deep Learning
EE 541 - Unit 1
Spring 2026
Deep Learning
How Neural Networks Learn
Learning to Classify
What is Machine Learning?
Learning = Task + Performance Measure + Experience
Herbert Simon (1983)
“Learning is any process by which a system improves performance from experience.”
Framework
\[\text{Learning System} = (\mathcal{T}, \mathcal{P}, \mathcal{E})\]
- Task \(\mathcal{T}\): What to accomplish
- Performance \(\mathcal{P}\): How to measure success
- Experience \(\mathcal{E}\): Data to learn from
Learning occurs when: \[\mathcal{P}_{\text{after}}(\mathcal{T}, \mathcal{E}) > \mathcal{P}_{\text{before}}(\mathcal{T})\]
Example: Email Spam Filter
- Task (\(\mathcal{T}\)): Classify emails as spam/not spam
- Performance (\(\mathcal{P}\)): % correctly classified
- Experience (\(\mathcal{E}\)): Database of labeled emails
Example: Self-Driving Car
- \(\mathcal{T}\): Navigate roads safely
- \(\mathcal{P}\): Miles without intervention
- \(\mathcal{E}\): Hours of human driving data
Generalization is the Goal of Machine Learning
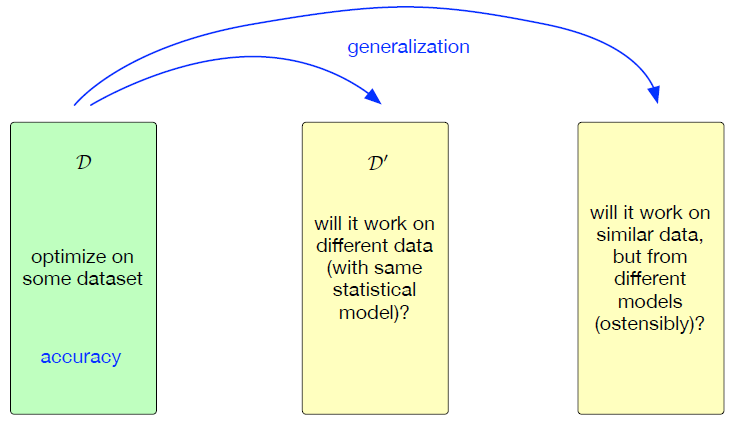
- Do not care about performance on the dataset we have
- Do care about performance on similar data that has no labels
- Accuracy/Generalization trade-off (bias-variance trade):
- Optimizing accuracy to the extreme reduces capability to generalize
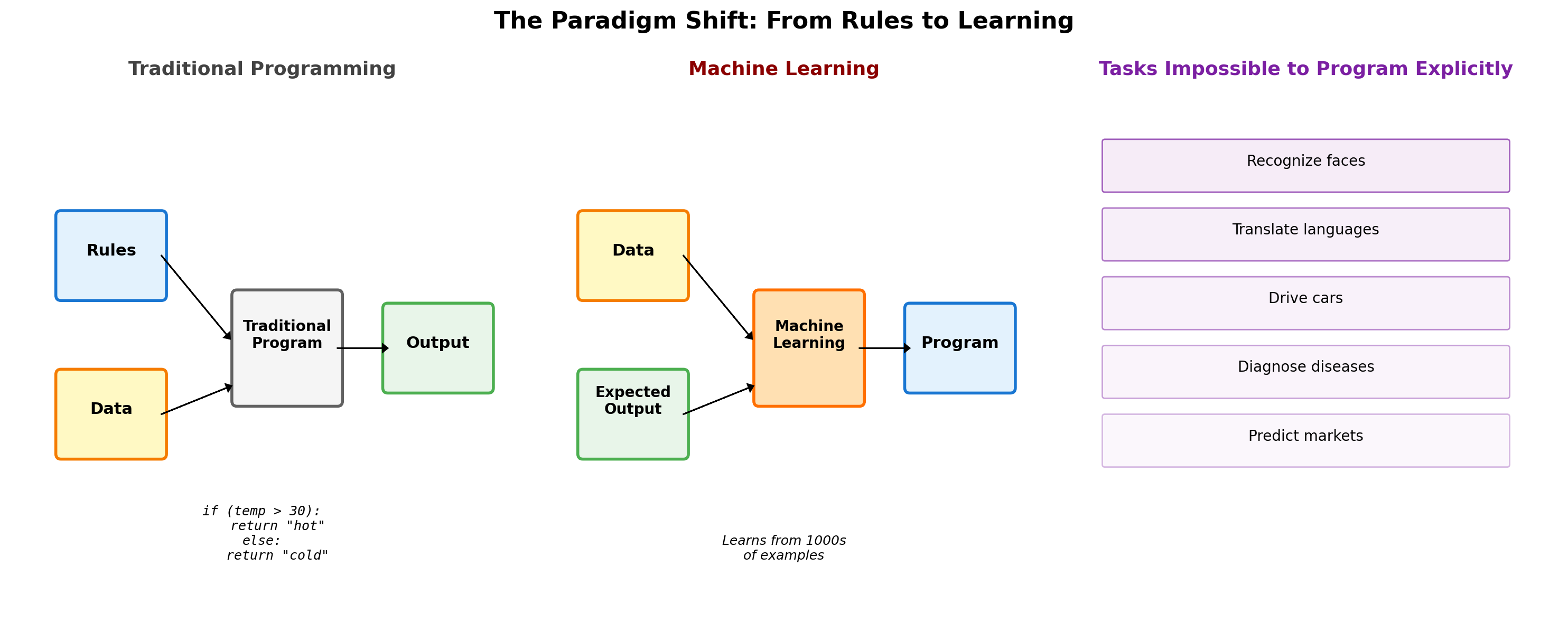
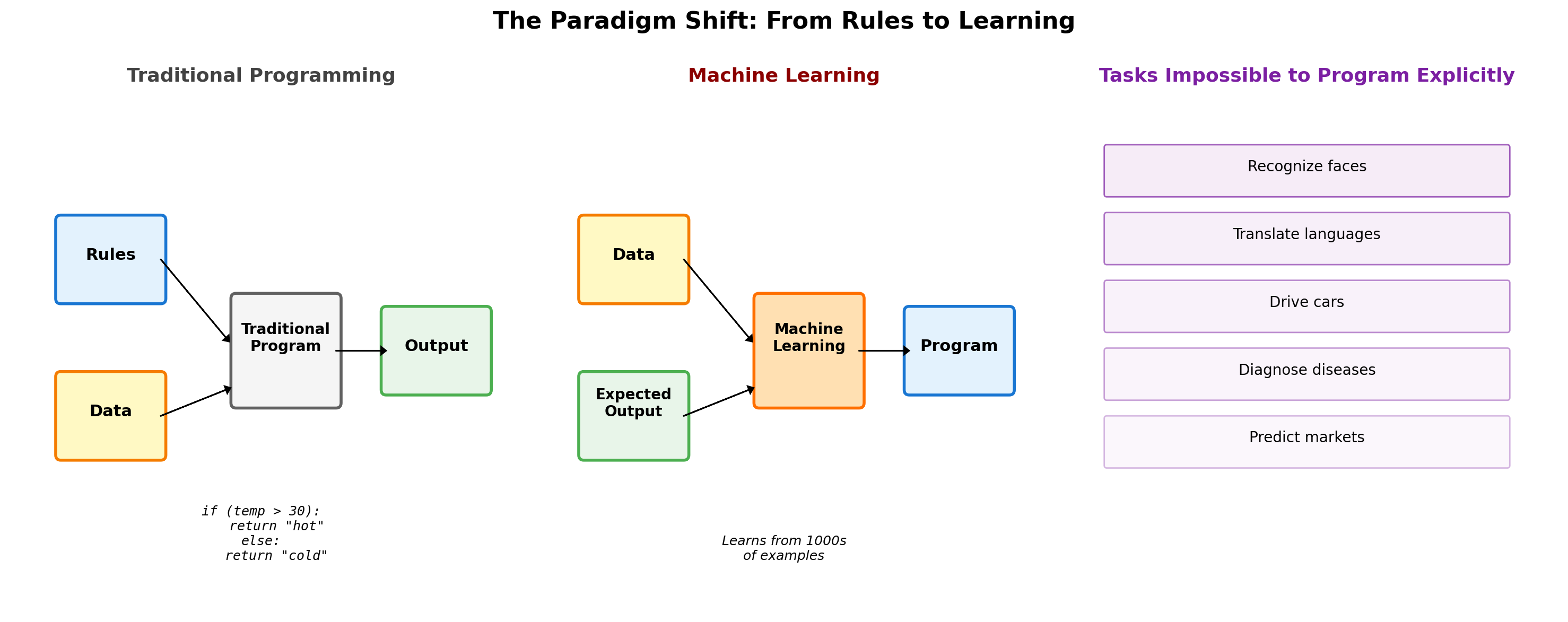
Machine Learning Inverts Traditional Programming
Theory-Driven vs Data-Driven Approaches
Classical: Theory-Driven
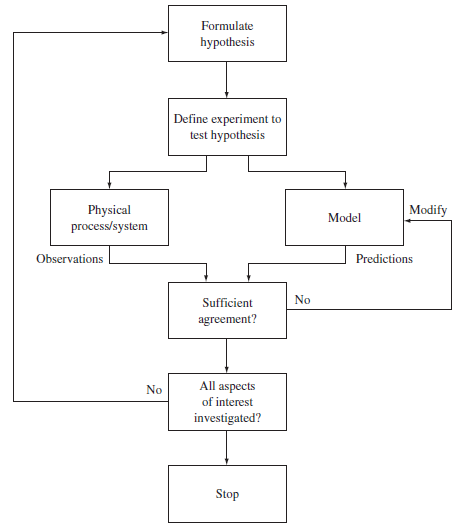
Modern: Data-Driven
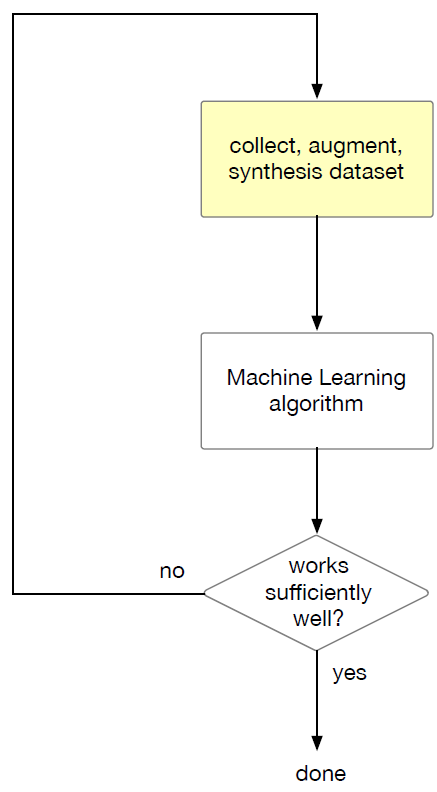
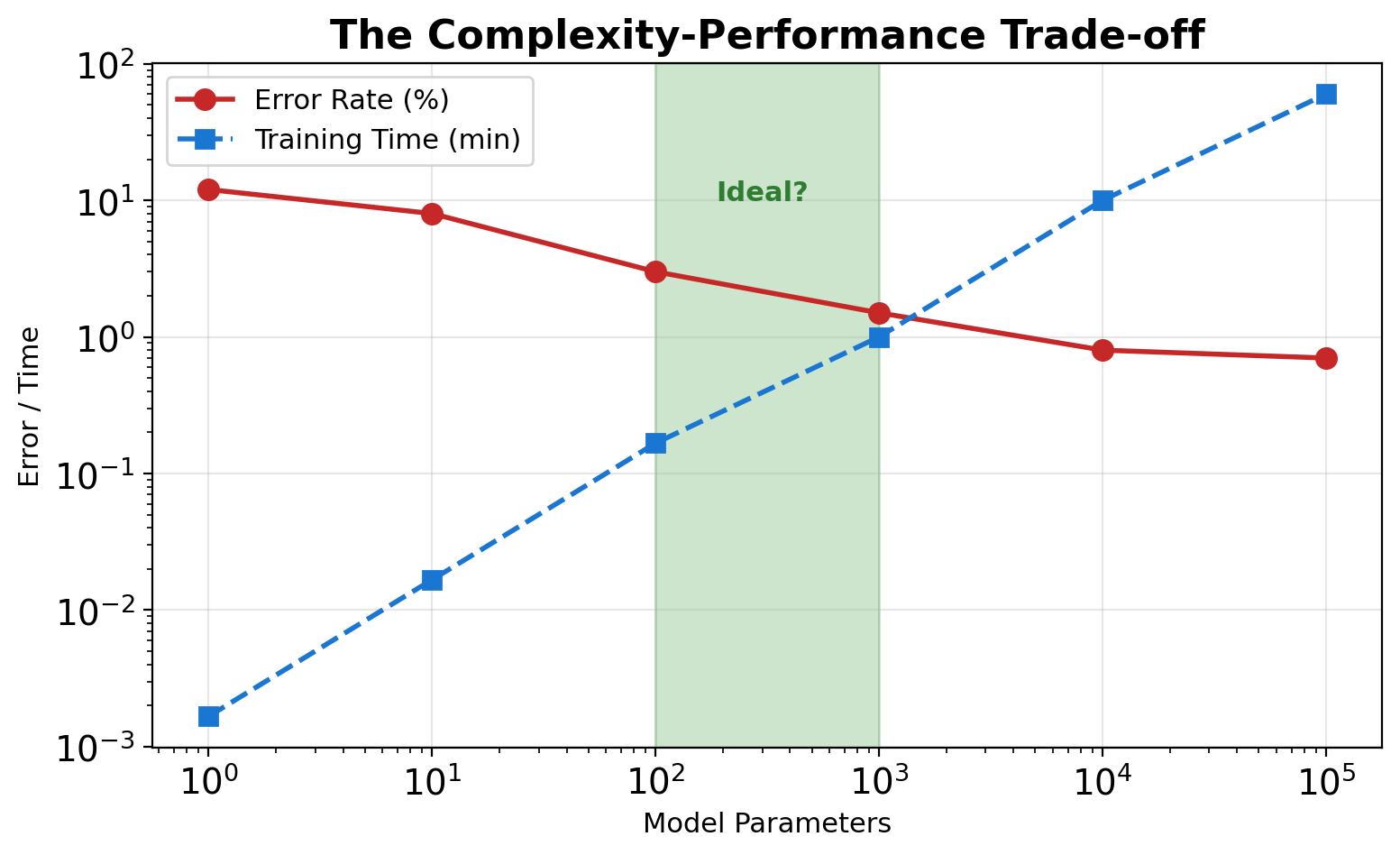
Model Complexity: When to Stop Adding Parameters
George Box (1976)
“All models are wrong, but some are useful”
“Since all models are wrong the scientist cannot obtain a ‘correct’ one by excessive elaboration”
Box’s warning: More parameters ≠ better science
MNIST Classification: Accuracy vs Complexity
- Nearest neighbor: 3% error, \(\mathcal{O}(n)\) inference
- Linear classifier: 8% error, \(\mathcal{O}(d)\) inference
- 2-layer network: 2% error, 50K parameters
- ConvNet (LeNet-5): 0.8% error, 60K parameters
- ResNet-50: 0.2% error, 25M parameters
Question: Is 0.2% → 0.1% worth 25M parameters?
Worrying Selectively
It is inappropriate to be concerned about mice when there are tigers abroad
- Start simple
- Add complexity purposefully
- Validate empirically
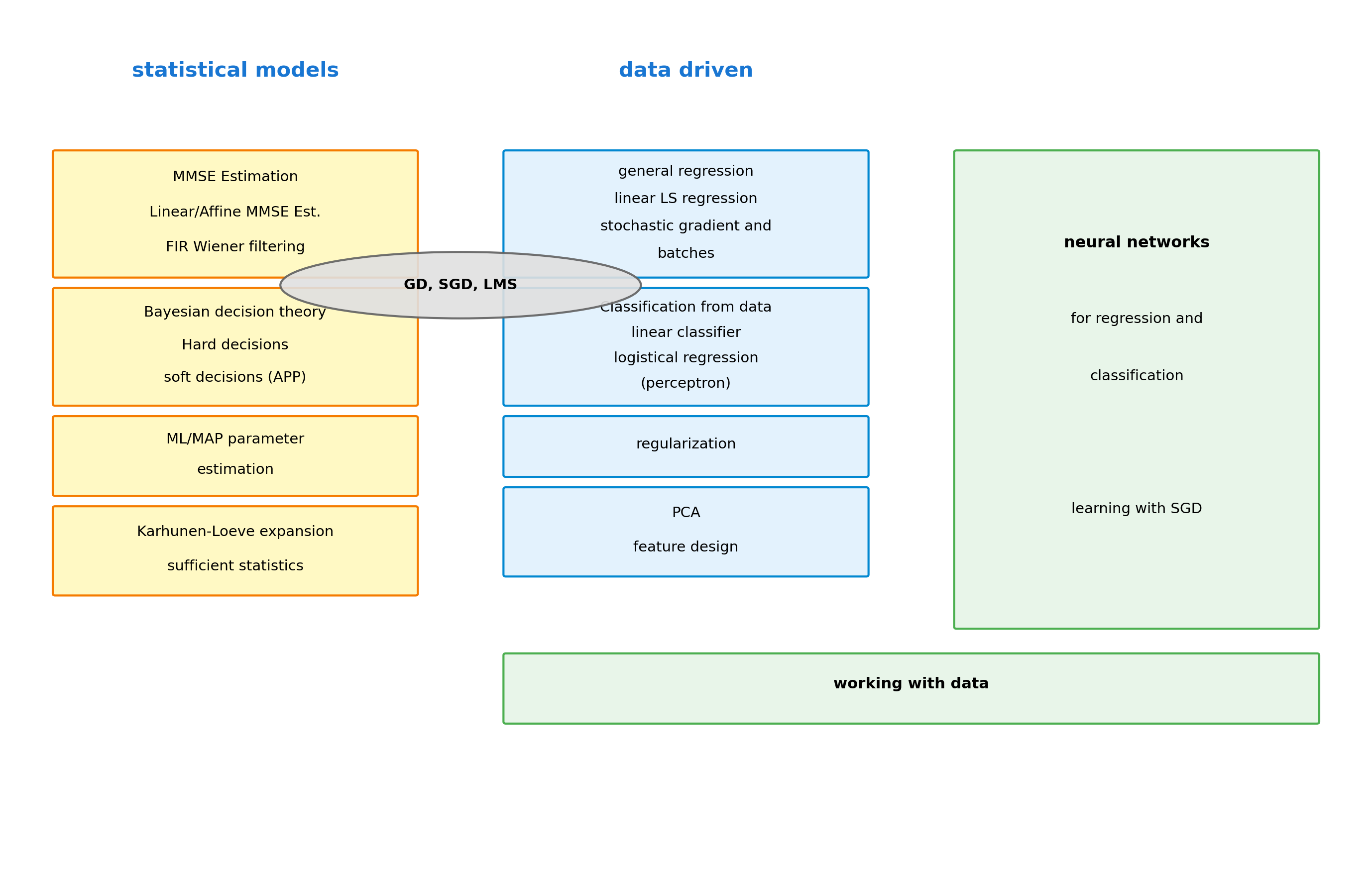
Course Structure: Statistical Foundations to Neural Networks
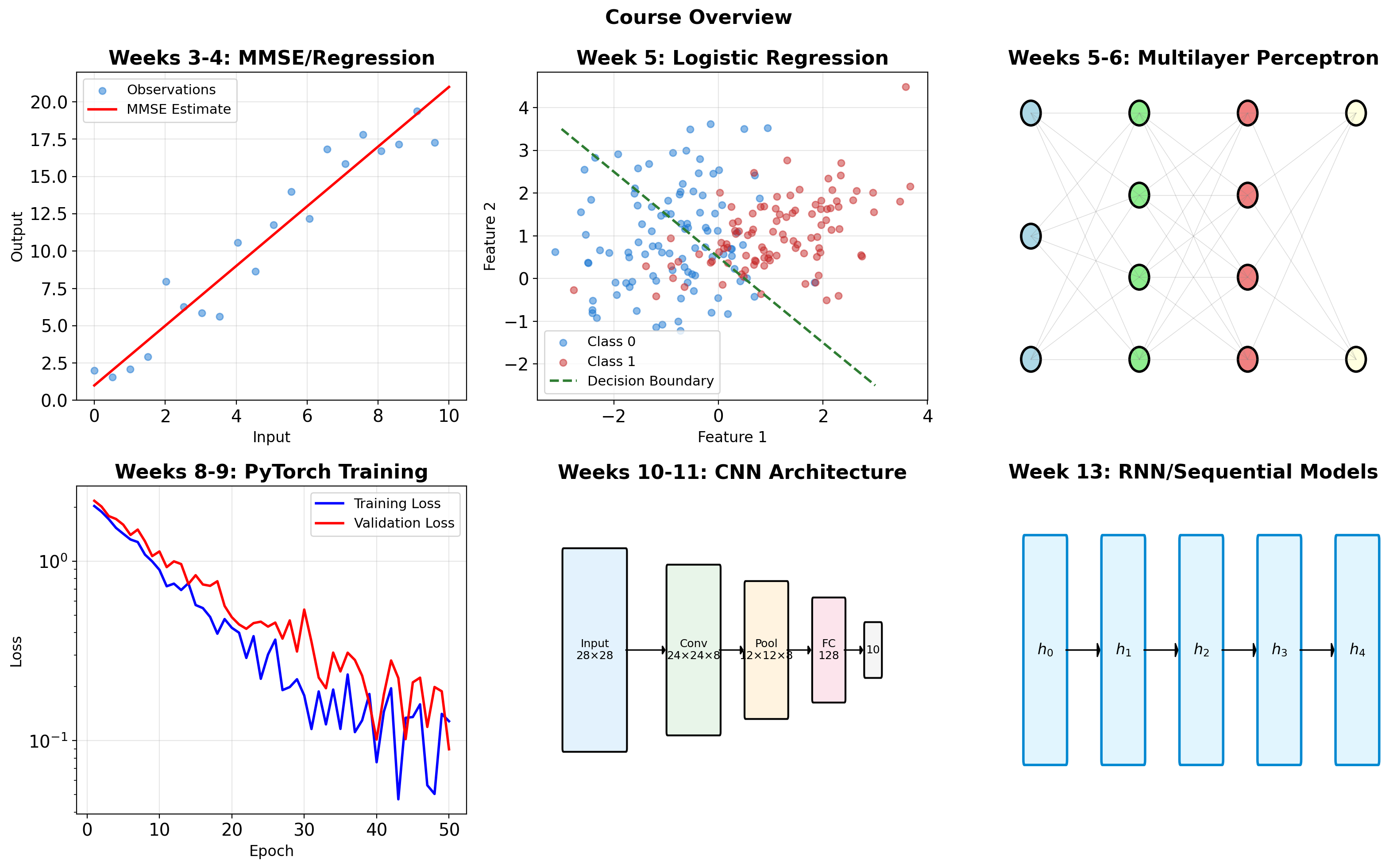
Semester Progression: MMSE to Convolutional Networks
Outline
Foundations
- Task, performance, experience
- Generalization as the goal
- Linear models and their limits
- Bias-variance tradeoff
- Quality vs quantity
- Representation and dimensionality
- Supervised, unsupervised, reinforcement
- Self-supervised methods
Neural Networks
- Perceptron to deep networks
- Universal approximation
- Width vs depth
- Loss landscapes
- SGD and variants
- The mystery of why networks work
Practice
- Fashion-MNIST classifier
Linear Models Fail on Nonlinear Boundaries
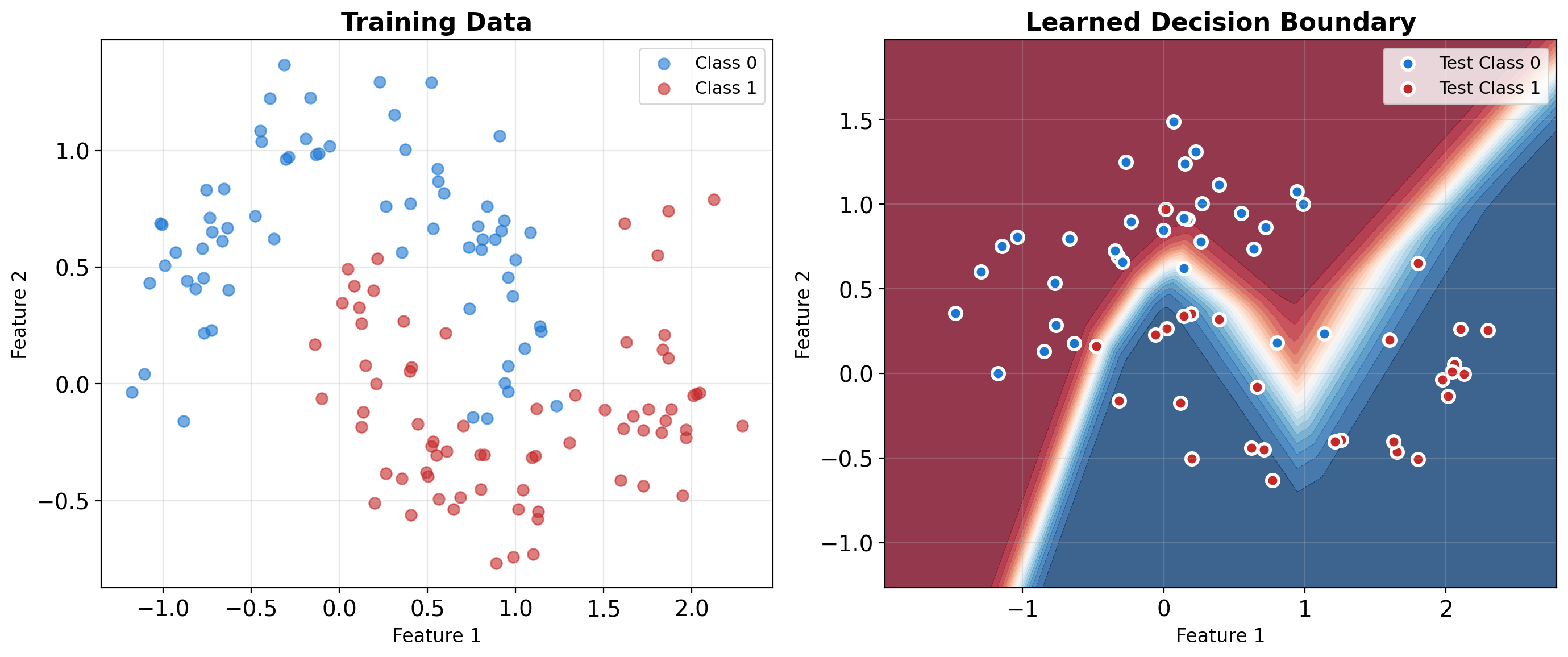
Two-Moons Dataset
Tests whether a model can learn curved decision boundaries. Two interleaving half-circles that cannot be separated by any straight line.
Neural Networks Learn Nonlinear Decision Boundaries
Code
import numpy as np
from sklearn.neural_network import MLPClassifier
from sklearn.datasets import make_moons
from sklearn.model_selection import train_test_split
X, y = make_moons(n_samples=200, noise=0.2, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.3, random_state=42
)
mlp = MLPClassifier(
hidden_layer_sizes=(10, 10),
max_iter=1000,
random_state=42
)
mlp.fit(X_train, y_train)
print(f"Training accuracy: {mlp.score(X_train, y_train):.3f}")
print(f"Test accuracy: {mlp.score(X_test, y_test):.3f}")Training accuracy: 0.979
Test accuracy: 0.950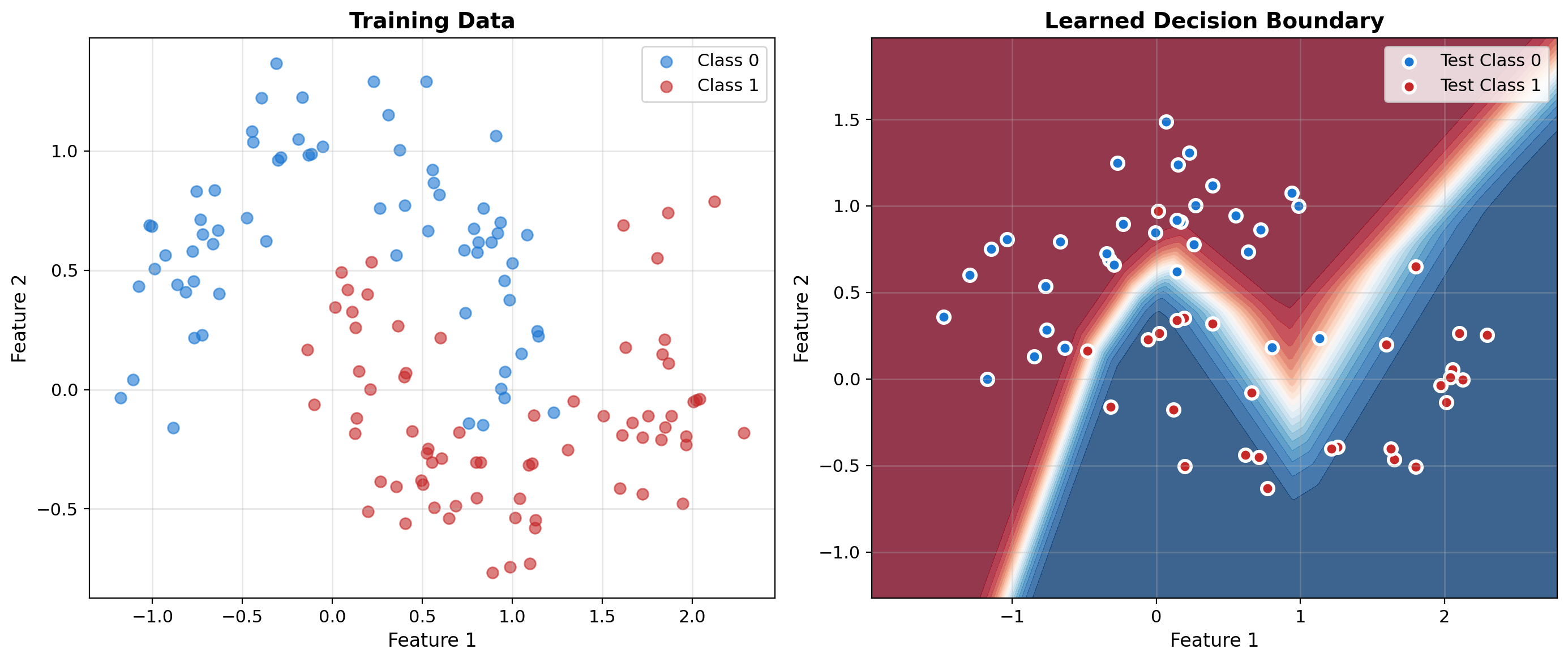
Learning Fundamentals
Minimize Expected Risk Using Only Finite Samples
Given
- Training data: \(\mathcal{D} = \{(\mathbf{x}_i, y_i)\}_{i=1}^N\)
- Hypothesis class: \(\mathcal{H}\)
- Loss function: \(\mathcal{L}\)
Goal
Find \(h^* \in \mathcal{H}\) that minimizes:
\[\mathbb{E}_{(\mathbf{x},y) \sim P}[\mathcal{L}(h(\mathbf{x}), y)]\]
But we only have access to:
\[\frac{1}{N}\sum_{i=1}^N \mathcal{L}(h(\mathbf{x}_i), y_i)\]
Generalization Gap
Minimize error on unseen data using only observed samples
This gap defines machine learning

Example Task: “2s” Detector

MNIST: Input and Output Representations
Input Space
- Raw pixels: \(\mathbf{x} \in \{0,255\}^{784}\)
- Normalized: \(\mathbf{x} \in [0,1]^{784}\)
- Binary: \(\mathbf{x} \in \{0,1\}^{784}\)
Output Space
- Classification: \(y \in \{0,1,...,9\}\)
- One-hot: \(\mathbf{y} \in \{0,1\}^{10}\)
- Probability: \(\mathbf{y} \in [0,1]^{10}\)
Same Data, Multiple Representations

Representation Determines Learnability
The choice of representation can make learning tractable or impossible. Deep learning learns representations automatically.
Example: The Data Domain
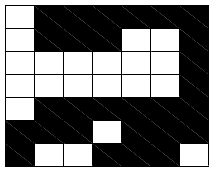
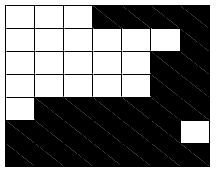

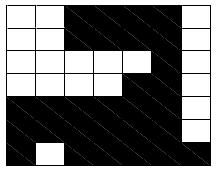
GOOD
GOOD
BAD
?
The choice of how to represent input is very important
Can we classify the unknown pattern?
Converting Pattern to Binary Vector

Binary Representation
x = 0111111011100100000010000
001011111111101111001110Label: “GOOD”
Key Insight
The same pattern can be represented as:
- Raw pixels
- Binary vectors (length d = 49)
- Feature vectors
- Learned representations
A hypothesis class can succeed or fail based on the choice of representation.
Linear Classifier on Binary Representation
Representation: Binary vectors, length \(d = 49\)
\[\mathbf{x} = \begin{bmatrix} 0111111011100100000010000 \\ 001011111111101111001110 \end{bmatrix}\]
\[y \in \{-1, +1\}\]
Hypothesize mapping data to label using linear classifier:
\[\hat{y} = \text{sign}(\mathbf{w} \cdot \mathbf{x}) = \text{sign}(w_1 x_1 + \cdots + w_{49} x_{49})\]
Definition: Linear Function
A function \(f: \mathbb{R}^d \rightarrow \mathbb{R}\) is linear if \(f(\mathbf{x}) = \mathbf{w}^\top \mathbf{x} + b\) for some \(\mathbf{w} \in \mathbb{R}^d\) and \(b \in \mathbb{R}\). The decision boundary \(\{\mathbf{x} : f(\mathbf{x}) = 0\}\) is a hyperplane.
where:
- \(\mathbf{w}\): Parameters to learn (weight vector)
- \(\hat{y}\): Predicted label (sign of linear combination)
Linear vs Nonlinear Hypothesis Classes
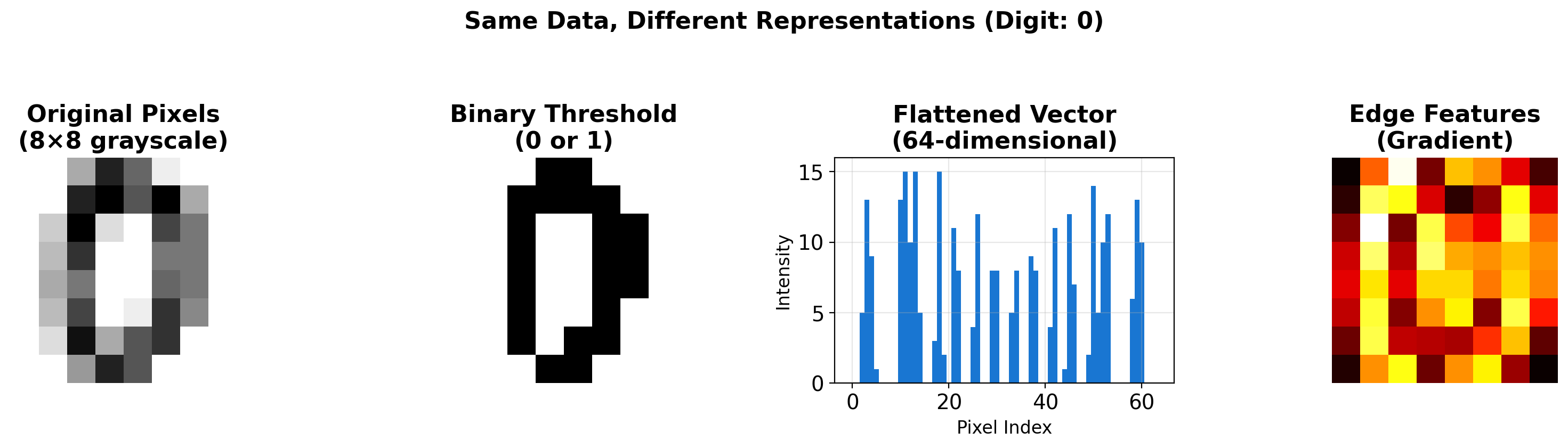
\[\mathcal{H}_{\text{linear}}: h(\mathbf{x}) = \text{sign}(\mathbf{w}^T\mathbf{x} + b)\] \[\mathcal{H}_{\text{neural}}: h(\mathbf{x}) = h_2(\mathbf{W}_2 \cdot h_1(\mathbf{W}_1\mathbf{x} + \mathbf{b}_1) + \mathbf{b}_2)\]
Perceptron: Linear Combination + Nonlinearity
Mathematical Model
\[y = h\left(\sum_{i=1}^n w_i x_i + b\right) = h(\mathbf{w}^T\mathbf{x} + b)\]
where \(h\) is an activation function:
- Step: \(h(z) = \begin{cases} 1 & z \geq 0 \\ 0 & z < 0 \end{cases}\)
- Sigmoid: \(h(z) = \frac{1}{1 + e^{-z}}\)
- ReLU: \(h(z) = \max(0, z)\)
Activation Functions Add Nonlinearity
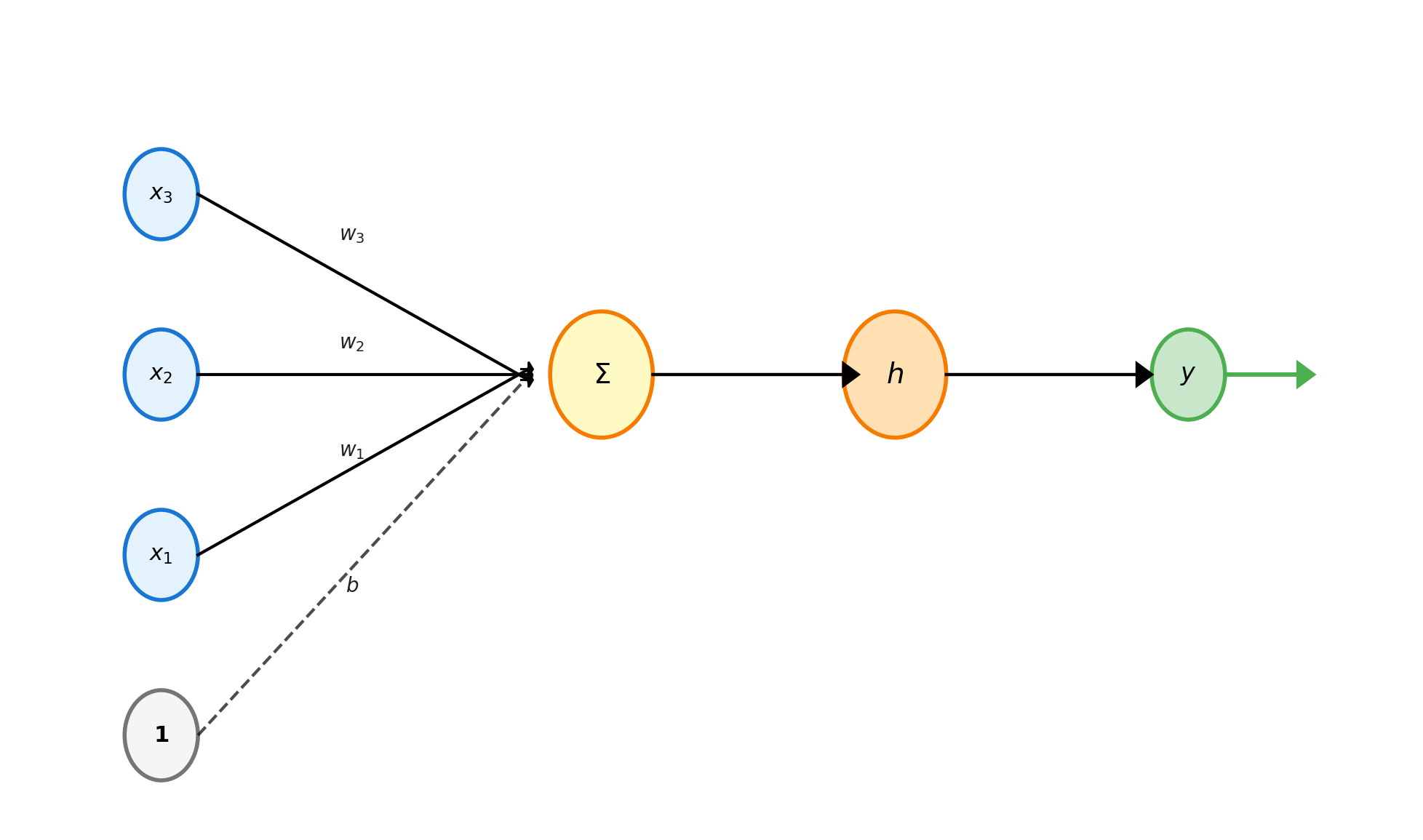
Why Nonlinearity Matters
Without activation functions, stacking layers is pointless: \(f(\mathbf{W}_2 \mathbf{W}_1 \mathbf{x}) = f(\mathbf{W} \mathbf{x})\) where \(\mathbf{W} = \mathbf{W}_2\mathbf{W}_1\)
Later topic: Gradient flow and vanishing gradients during backpropagation
Closed-Form vs Iterative Optimization
Explicit (Closed-form)
\[\mathbf{w}^* = \arg\min_{\mathbf{w}} \|\mathbf{y} - \mathbf{X}\mathbf{w}\|^2\]
Solution: \[\mathbf{w}^* = (\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{y}\]
- One-shot computation
- Requires matrix inversion
- Memory intensive for large data
Iterative (Gradient-based)
\[\mathbf{w}_{t+1} = \mathbf{w}_t - \eta \nabla_{\mathbf{w}}\mathcal{L}(\mathbf{w}_t)\]
- Sequential updates
- Scales to large datasets
- Foundation of deep learning
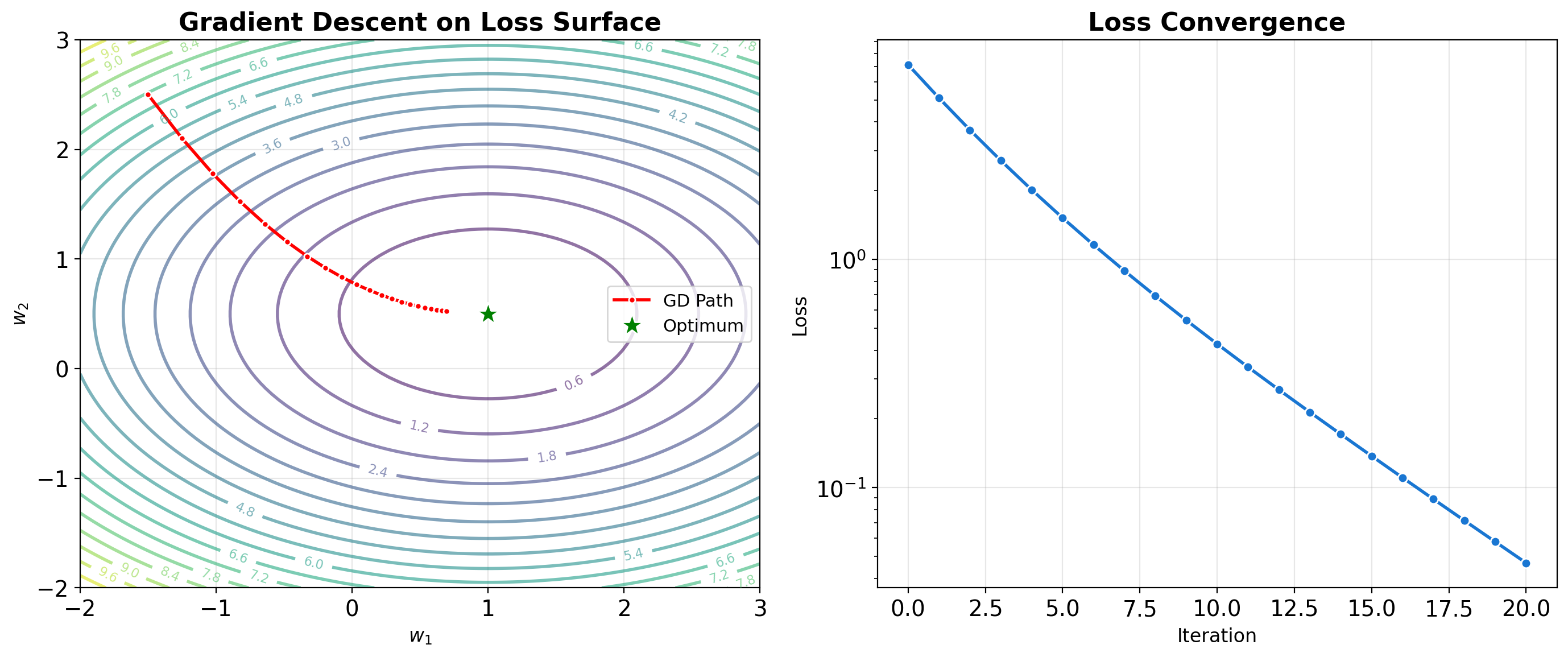
Gradient Descent Visualization
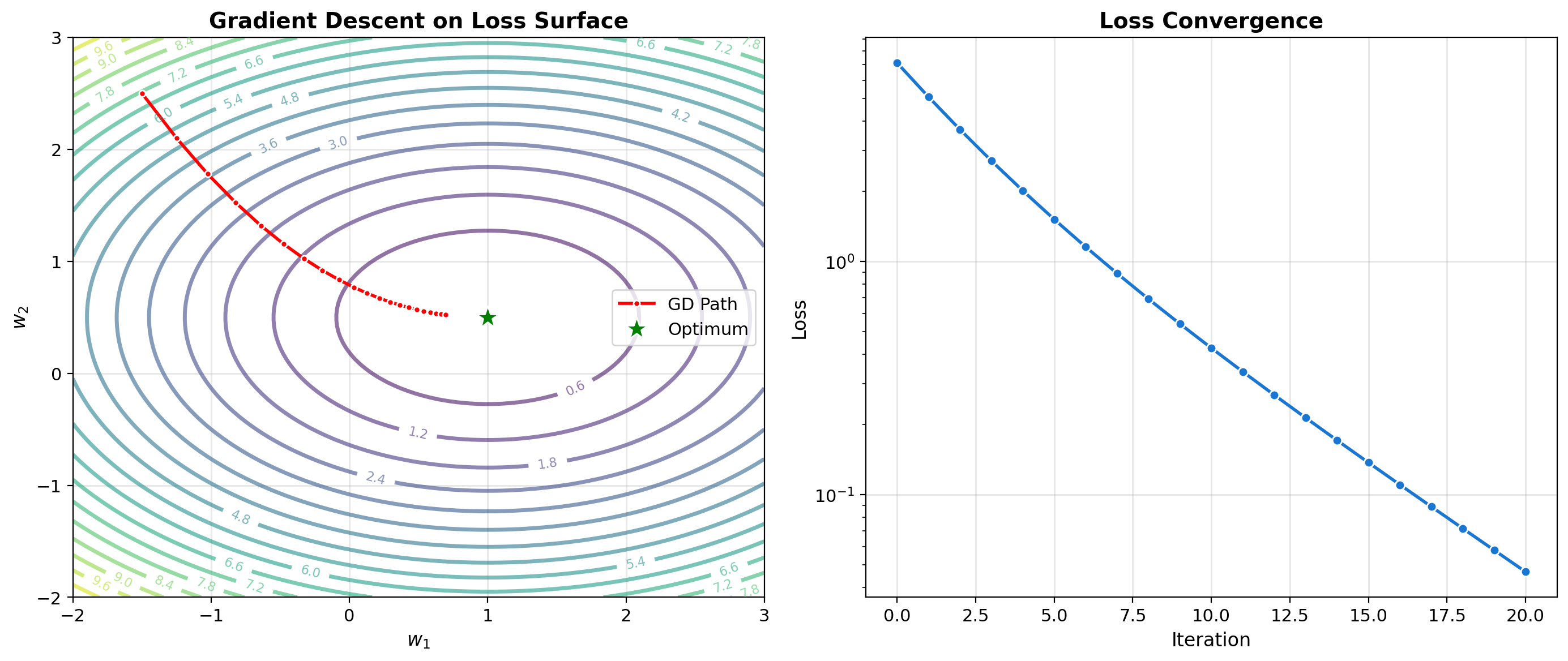
Iterative Optimization Principle
Gradient descent navigates the loss landscape by repeatedly moving in the direction of steepest descent. For convex problems, this guarantees convergence to the global minimum. For neural networks, we settle for local minima that generalize well.
The Bias-Variance Decomposition
Expected Prediction Error
\[\text{MSE} = \text{Bias}^2 + \text{Variance} + \sigma^2\]
Bias: Error from wrong model assumptions
- High bias: Model too simple (underfits)
- Low bias: Model captures true pattern
Variance: Error from sensitivity to training data
- High variance: Model memorizes noise (overfits)
- Low variance: Model finds generalizable pattern
Irreducible error (\(\sigma^2\)): Noise inherent in data
Tradeoff: Complex models reduce bias but increase variance
Bias-Variance in Practice: Polynomial Fitting
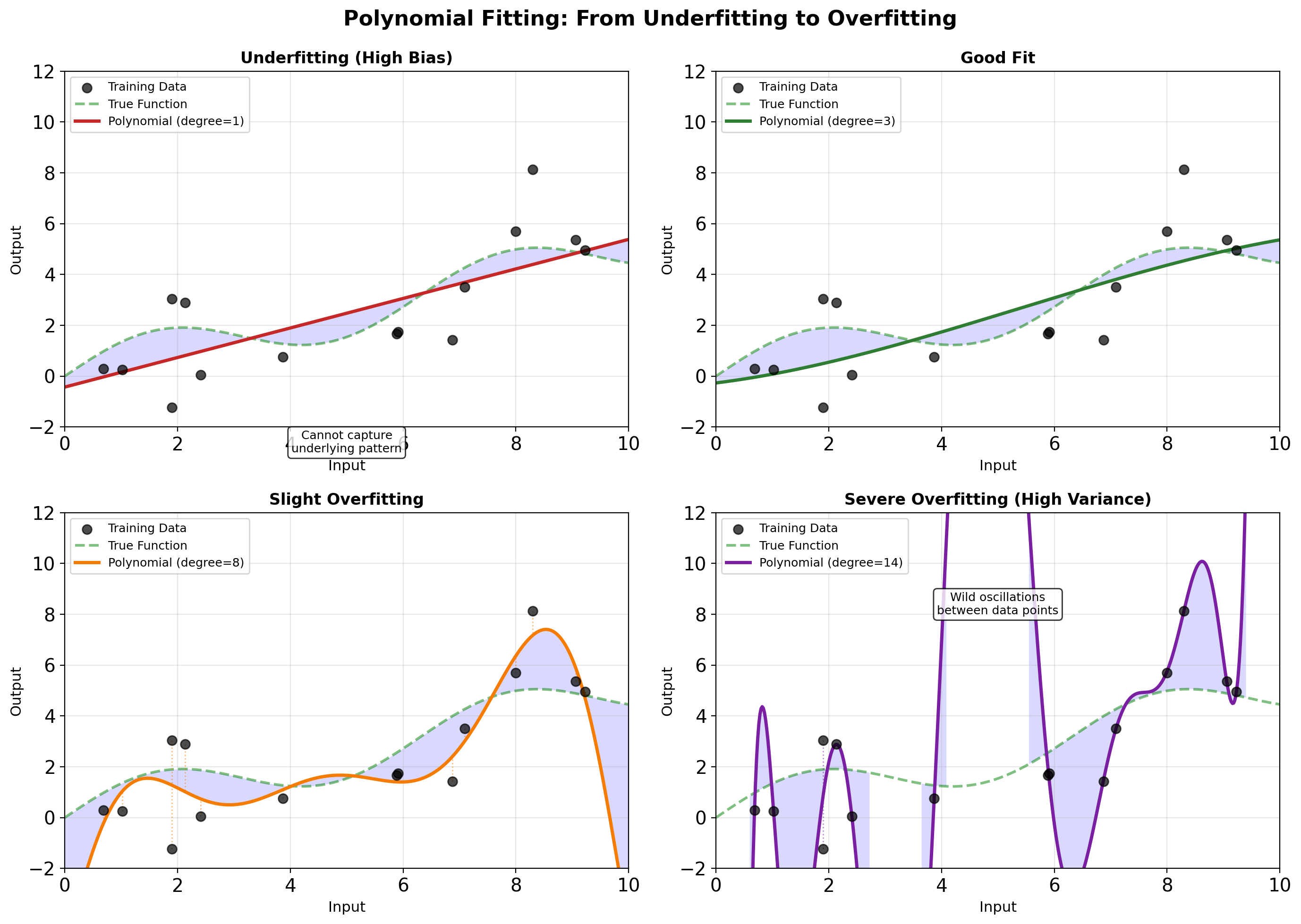
- Degree 1: Too simple, systematic error (high bias)
- Degree 3: Captures pattern without noise
- Degree 8: Starts fitting noise
- Degree 14: Wild oscillations (high variance)
Increasing complexity: bias decreases, variance increases
EE 541 Core Principles
Theory
Learning = Function Approximation
- From data to predictions
- Hypothesis class defines possibilities
Representation Matters
- Same data, different encodings
- Deep learning learns representations
Generalization is the Goal
- Not memorization
- Balance complexity with data
Implementation
- Start Simple
- Linear models as baselines
- Add complexity purposefully
- Iterate and Validate
- Gradient descent scales
- Monitor train vs test error
- EE 541 Progression
- MMSE → Regression → Neural Nets
- Theory + PyTorch implementation
Listen to the Data
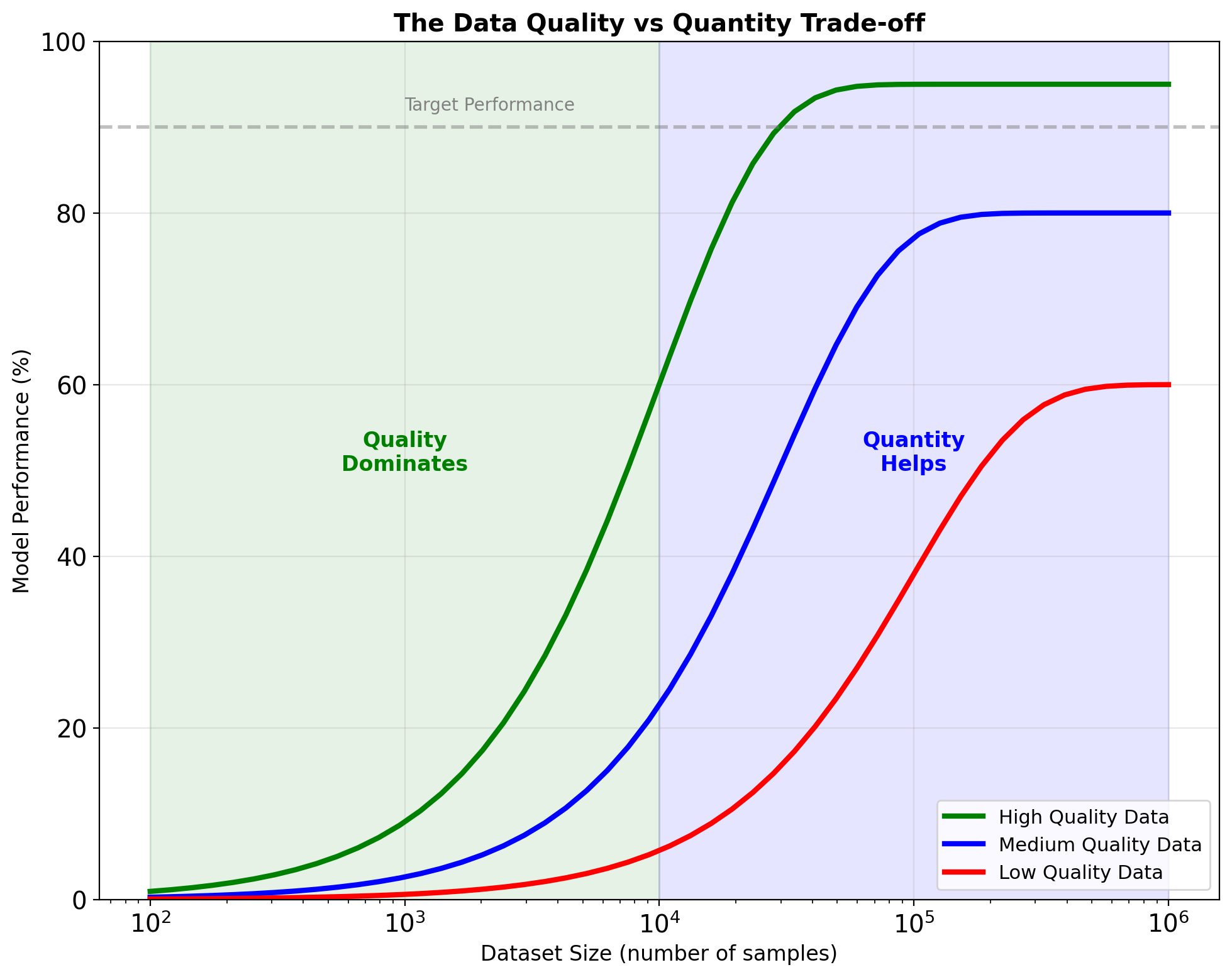
Data Quality Dominates Quantity
Clive Humby (2006)
“Data is the new oil”
But like oil, it must be refined to have value
\[\text{Model Performance} = f(\text{Data Quality}, \text{Data Quantity})\]
Illustrative Example: Data Refinement Impact
- Raw data: 10% usable (mislabeled, corrupted, outliers)
- Cleaned data: 40% usable (errors removed, imputed)
- Curated data: 90% usable (validated, balanced, relevant)
Note: Specific percentages vary by application, but quality improvement consistently outperforms quantity alone.
Representation Transforms Problem Difficulty
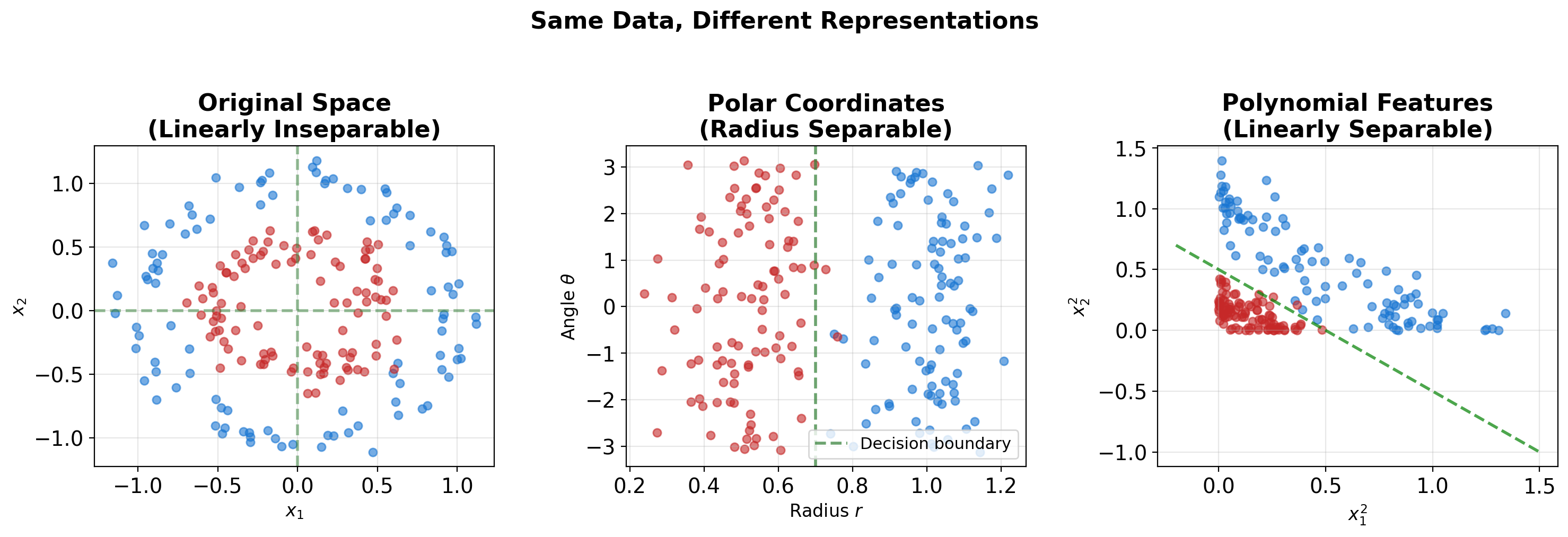
Representation Determines Learnability
Concentric circles: linearly inseparable in Cartesian coordinates, but trivially separable by radius in polar coordinates. Deep learning automates this search for effective representations.
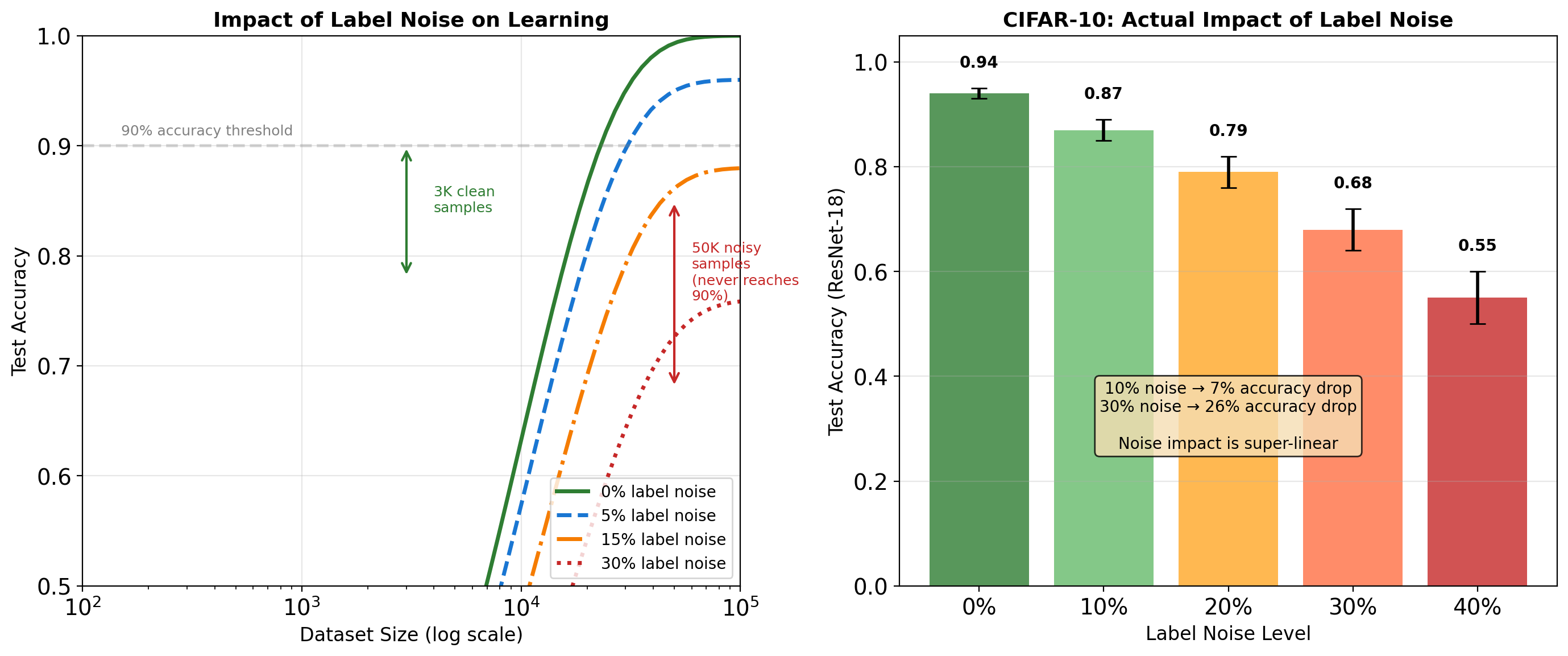
High Dimensions Break Geometric Intuition
The Curse of Dimensionality
As \(d \to \infty\):
- All points become equidistant
- Volume concentrates at surface
- Gaussian looks like uniform
- Nearest neighbors aren’t “near”
Code
d= 1: 0.050000 in outer shell
d= 2: 0.097500 in outer shell
d= 3: 0.142625 in outer shell
d= 10: 0.401263 in outer shell
d= 100: 0.994079 in outer shell
d=1000: 1.000000 in outer shell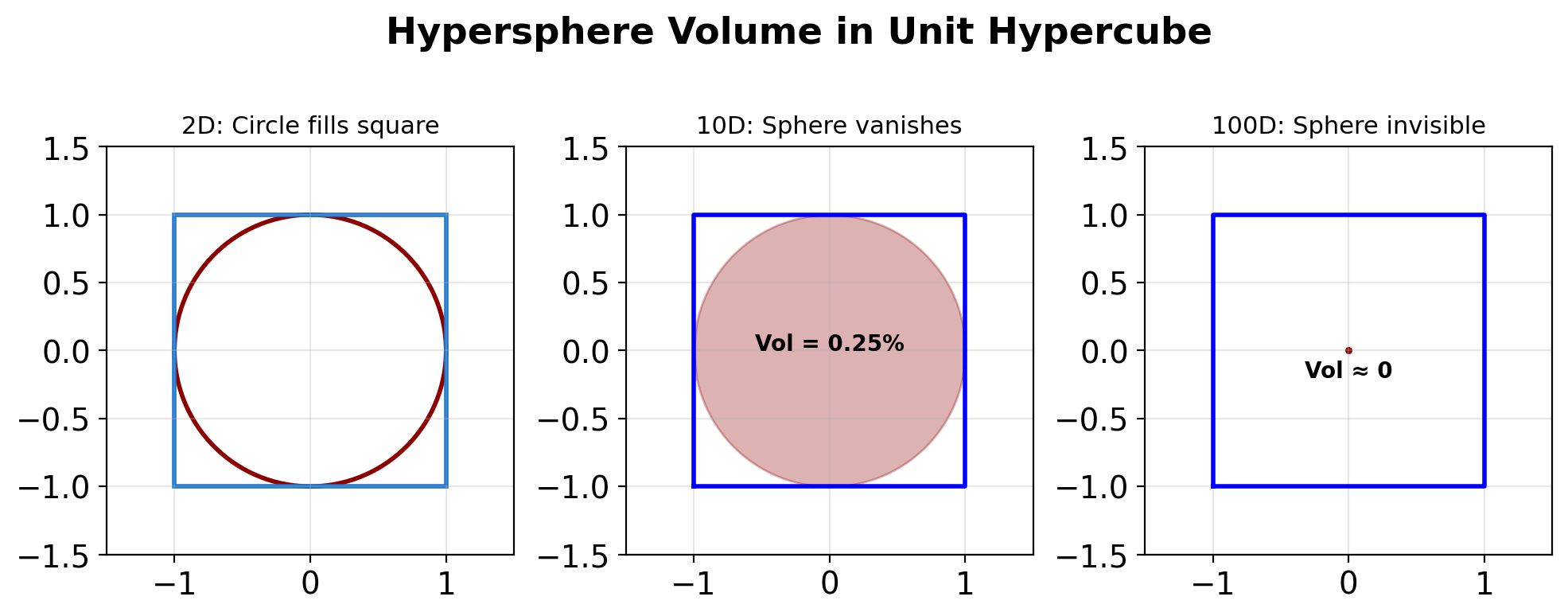
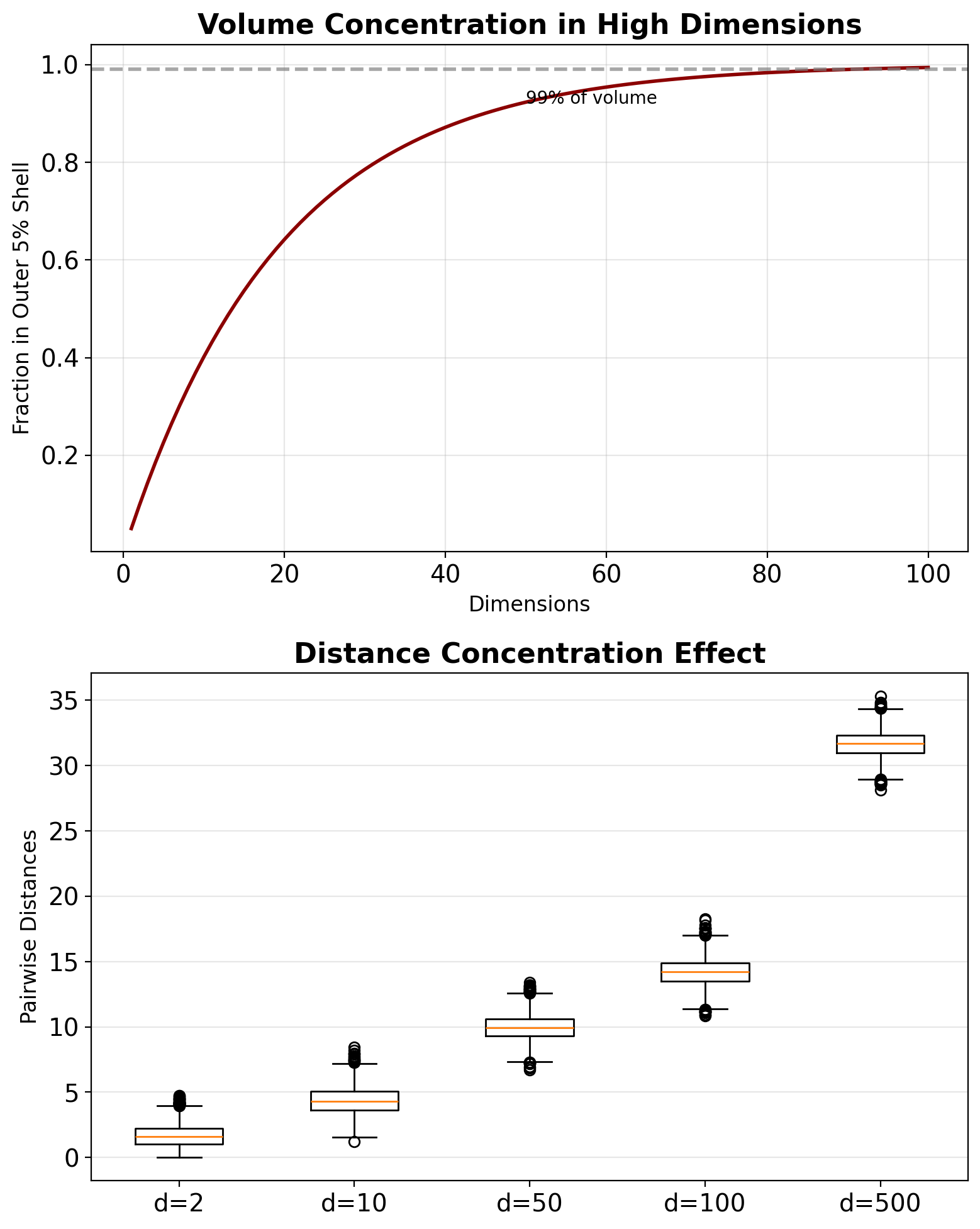
Label Noise Degrades Performance More Than Limited Data
Amazon Resume Screening: Training on Biased Data
Setup (2014-2017):
- Train model on 10 years of hiring decisions
- Input: resumes → Output: 1-5 star rating
- Goal: automate screening for top candidates
What went wrong:
- Model penalized resumes with “women’s chess club”
- Model penalized graduates of all-women’s colleges
- Model learned patterns from biased historical data
The data:
Historical hires: 85% male, 15% female
Model learned: male-coded patterns = higher ratingSystem scrapped in 2018.

Why this matters:
The model did exactly what it was trained to do - replicate patterns in historical data.
The problem: historical data reflected real-world bias.
Clean data ≠ unbiased data
- Data was accurate (real hiring decisions)
- Data was complete (10 years of records)
- Data was biased (reflected industry demographics)
Data Augmentation: Synthetic Diversity from Limited Samples
Standard Augmentations
- Geometric: Rotation, flip, crop, scale
- Photometric: Brightness, contrast, color
- Noise: Gaussian, dropout, cutout
- Advanced: Mixup, CutMix, AutoAugment
Mathematical View
Training on augmented data: \[\min_\theta \sum_{i=1}^N \sum_{j=1}^M \mathcal{L}(f_\theta(T_j(x_i)), y_i)\]
where \(T_j\) are augmentation transforms
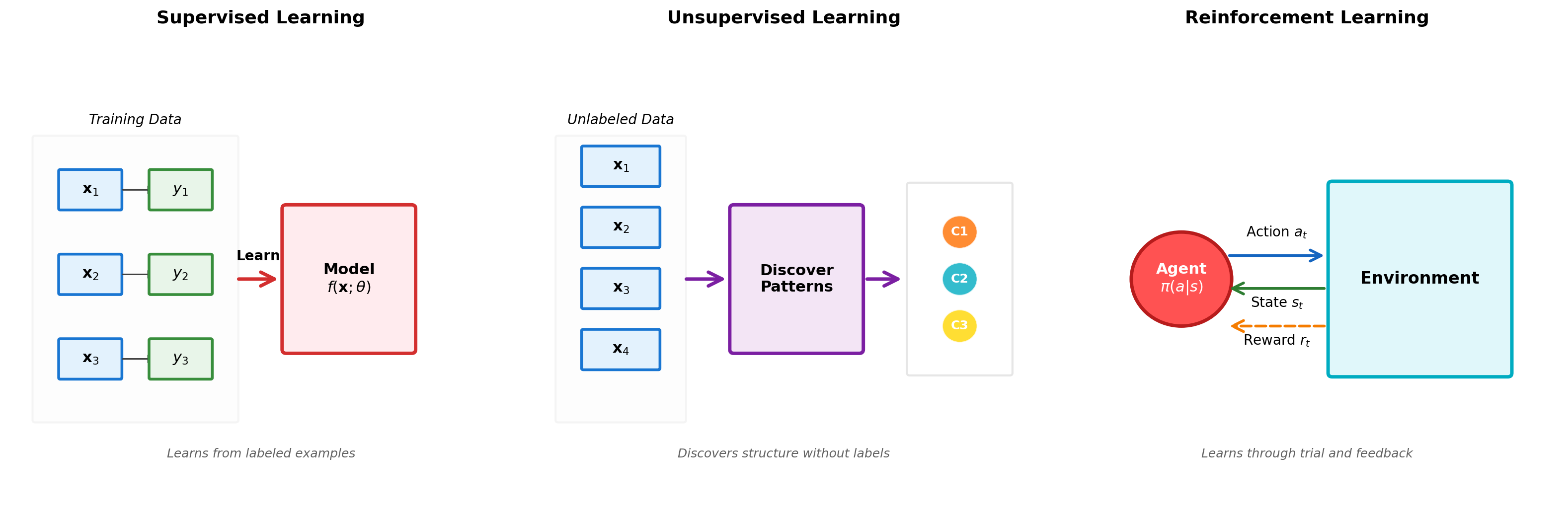
ML Learning Paradigms
Three Paradigms: Supervised, Unsupervised, Reinforcement
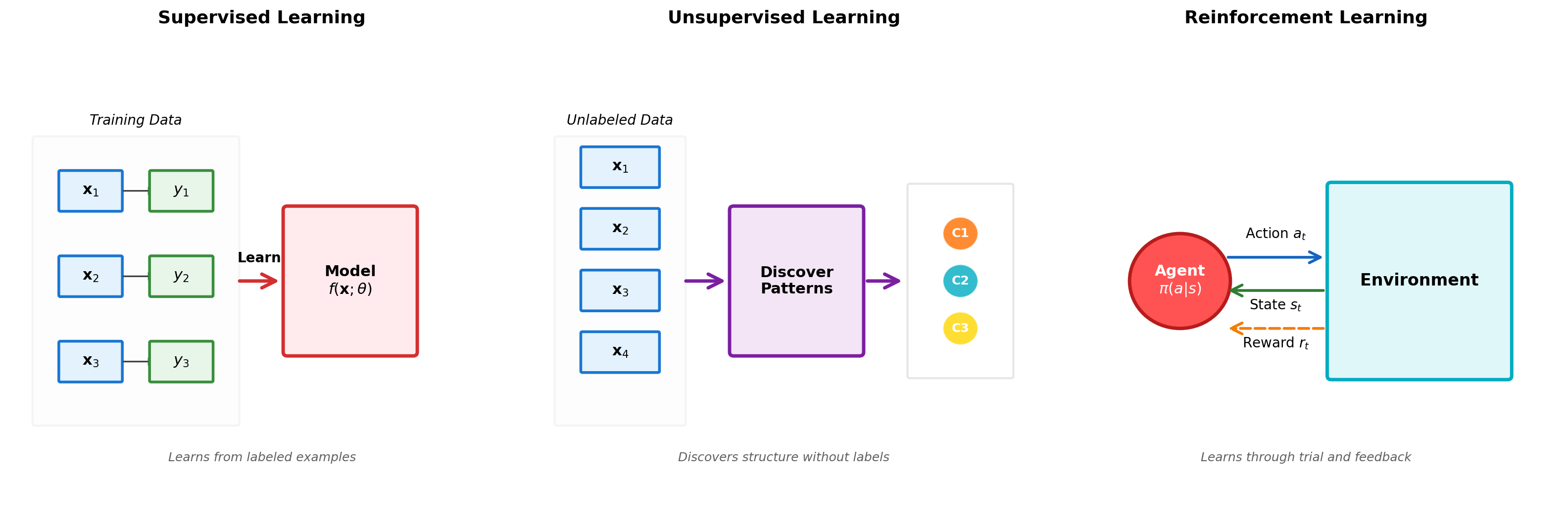
Modern methods combine paradigms: GPT-4 uses unsupervised pre-training on text, supervised fine-tuning on tasks, and reinforcement learning from human feedback (RLHF).
Supervised Learning: Labeled Data to Function Mapping
Problem Formulation
Given: \(\mathcal{D} = \{(\mathbf{x}_i, y_i)\}_{i=1}^N\)
Learn: \(f: \mathcal{X} \to \mathcal{Y}\)
Minimize: \(\mathcal{L}(f(\mathbf{x}), y)\)
Core Tasks
- Classification: \(y \in \{1, ..., C\}\)
- Regression: \(y \in \mathbb{R}^d\)
- Structured Prediction: \(y \in \mathcal{Y}_{\text{complex}}\)
Modern Applications
- Medical diagnosis from images
- Speech recognition
- Machine translation
- Time series forecasting
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
# Generate synthetic data
np.random.seed(42)
X = np.random.randn(1000, 10)
w_true = np.random.randn(10)
y = (X @ w_true + np.random.randn(1000)*0.1 > 0).astype(int)
# Standard supervised pipeline
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.2, random_state=42
)
model = LogisticRegression(max_iter=1000)
model.fit(X_train, y_train)
train_acc = accuracy_score(y_train, model.predict(X_train))
test_acc = accuracy_score(y_test, model.predict(X_test))
print(f"Train accuracy: {train_acc:.3f}")
print(f"Test accuracy: {test_acc:.3f}")Train accuracy: 0.990
Test accuracy: 0.995Supervised Learning Training and Inference

Training Phase
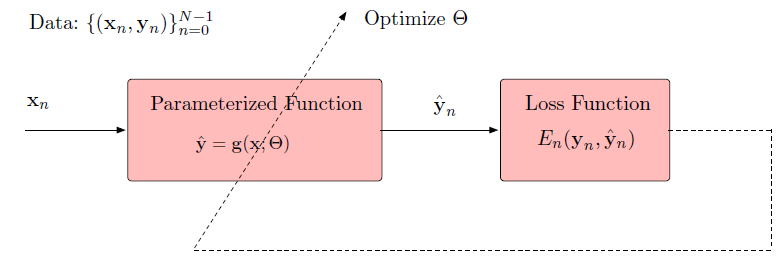
Inference Phase

Unsupervised Learning: Structure from Unlabeled Data
No Labels, Just Data
Given: \(\mathcal{D} = \{\mathbf{x}_i\}_{i=1}^N\)
Find: Hidden patterns, structure, representations
Key Methods
- Clustering: K-means, DBSCAN, hierarchical
- Dimensionality Reduction: PCA, t-SNE, UMAP
- Density Estimation: GMM, KDE
- Representation Learning: Autoencoders
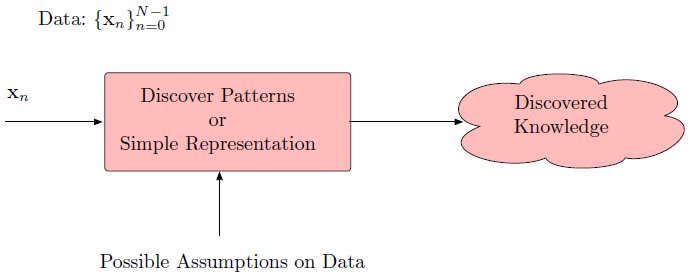
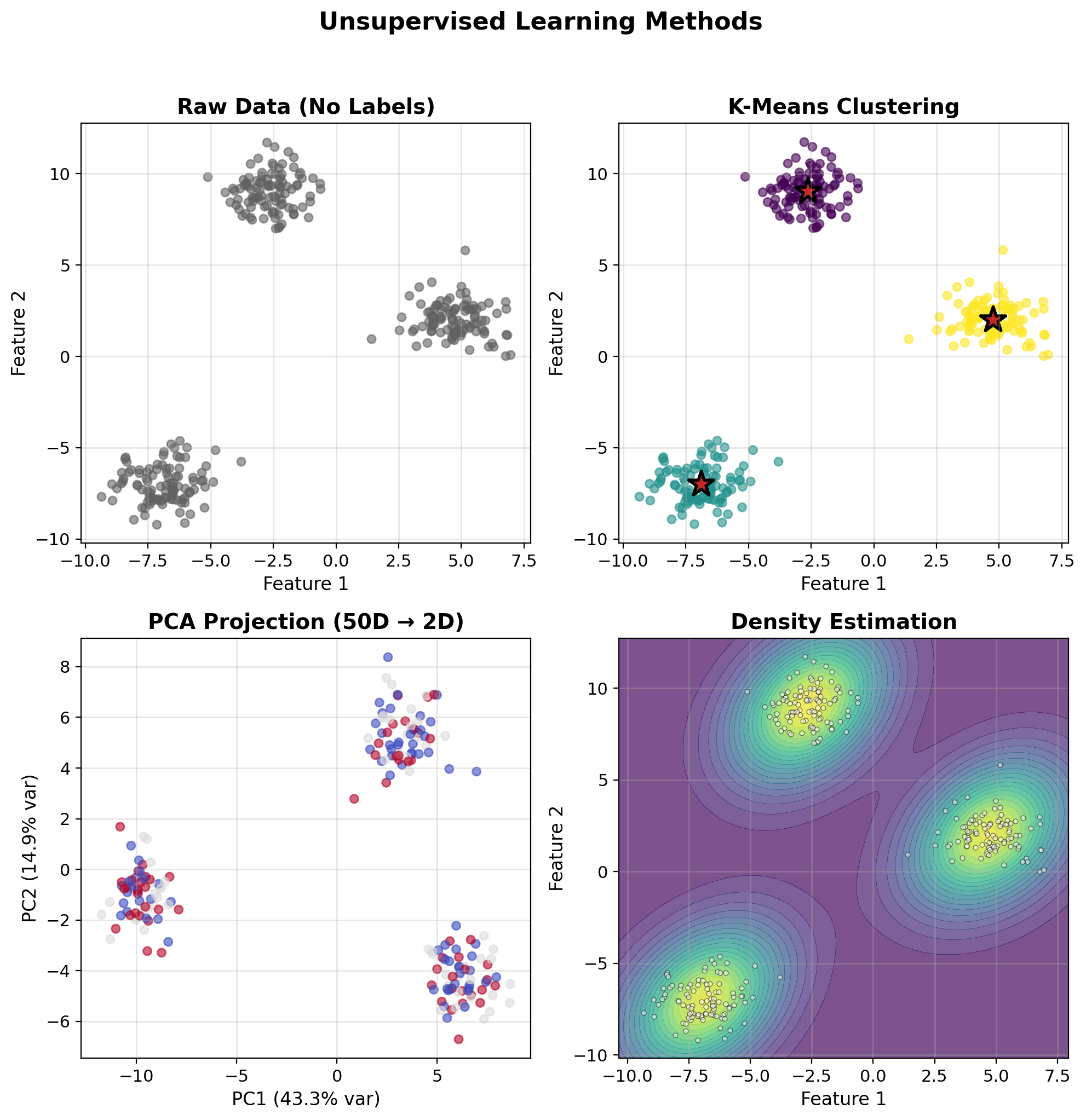
Clustering Reveals Hidden Patterns
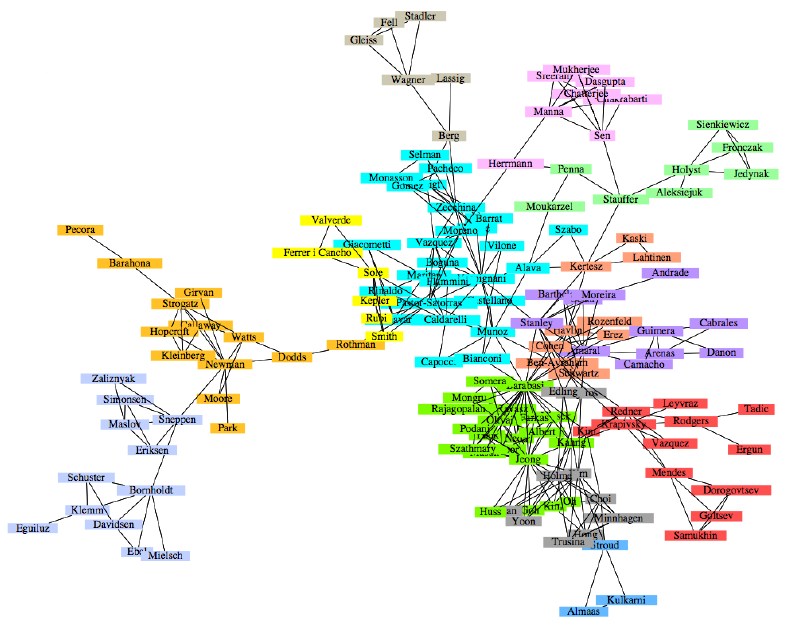
Finding Structure in Data
Self-Supervised Learning: Labels from Data Itself
Creating Supervision from Data
Transform unsupervised → supervised by creating pretext tasks
Key Innovations
- Language Models: Predict next word (GPT)
- Masked Modeling: Predict masked parts (BERT)
- Contrastive Learning: Similar/different pairs (SimCLR)
Why It Works
- Unlimited labeled data (self-generated)
- Learns general representations
- Transfer learning to downstream tasks
Code
# Example: Simple masked prediction
def create_masked_task(sequence, mask_prob=0.15):
"""Create self-supervised task from sequence"""
masked = sequence.copy()
labels = np.full_like(sequence, -1)
mask_indices = np.random.random(len(sequence)) < mask_prob
masked[mask_indices] = 0 # [MASK] token
labels[mask_indices] = sequence[mask_indices]
return masked, labels
# Example sequence
sequence = np.array([1, 4, 2, 8, 3, 7, 5, 9])
masked_input, targets = create_masked_task(sequence)
print(f"Original: {sequence}")
print(f"Masked: {masked_input}")
print(f"Targets: {targets}")Original: [1 4 2 8 3 7 5 9]
Masked: [1 0 0 0 3 0 5 9]
Targets: [-1 4 2 8 -1 7 -1 -1]Foundation Models and Self-Supervision
Self-supervised learning powers modern foundation models like GPT and BERT
Reinforcement Learning: Sequential Decision Making
Sequential Decision Making
Components:
- State space: \(\mathcal{S}\)
- Action space: \(\mathcal{A}\)
- Reward function: \(R(s, a)\)
- Policy: \(\pi(a|s)\)
Objective: Maximize expected cumulative reward \[J(\pi) = \mathbb{E}_{\pi}\left[\sum_{t=0}^{\infty} \gamma^t r_t\right]\]
Applications
- Game playing (Chess, Go, StarCraft)
- Robotics control
- Resource allocation
- Trading strategies
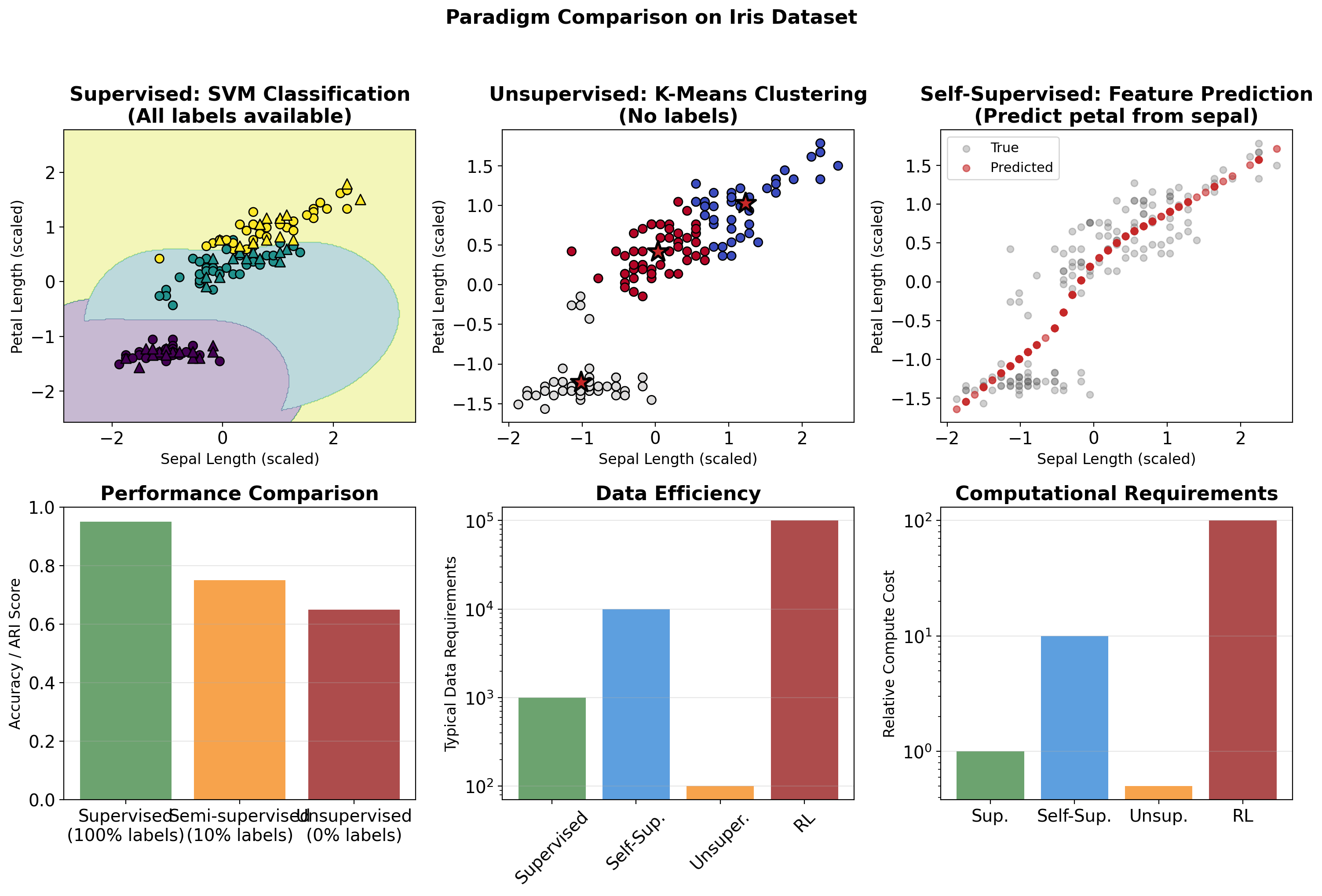
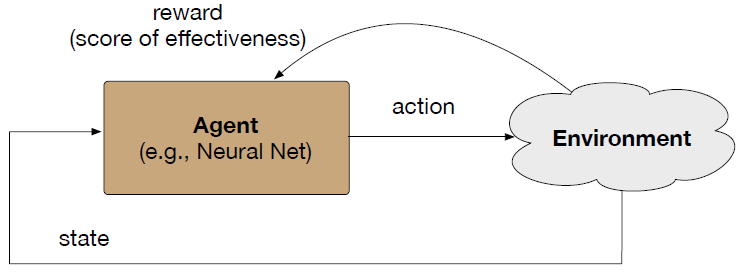
Same Problem, Different Paradigms
Label efficiency on CIFAR-10 (target: 90% accuracy):
- Supervised (full labels): 50,000 labeled images
- Semi-supervised (10% labels): 5,000 labeled + 45,000 unlabeled
- Self-supervised pretraining + fine-tune: 1,000 labeled (after ImageNet pretraining)
Transfer learning with self-supervised pretraining: 50× reduction in labeled data
Modern Methods Combine Paradigms
Semi-Supervised Learning
- Use small labeled + large unlabeled data
- Pseudo-labeling, consistency regularization
- Example: FixMatch, MixMatch
Multi-Task Learning
- Learn multiple related tasks simultaneously
- Shared representations
- Example: BERT for multiple NLP tasks
Meta-Learning
- Learn to learn
- Few-shot adaptation
- Example: MAML, Prototypical Networks
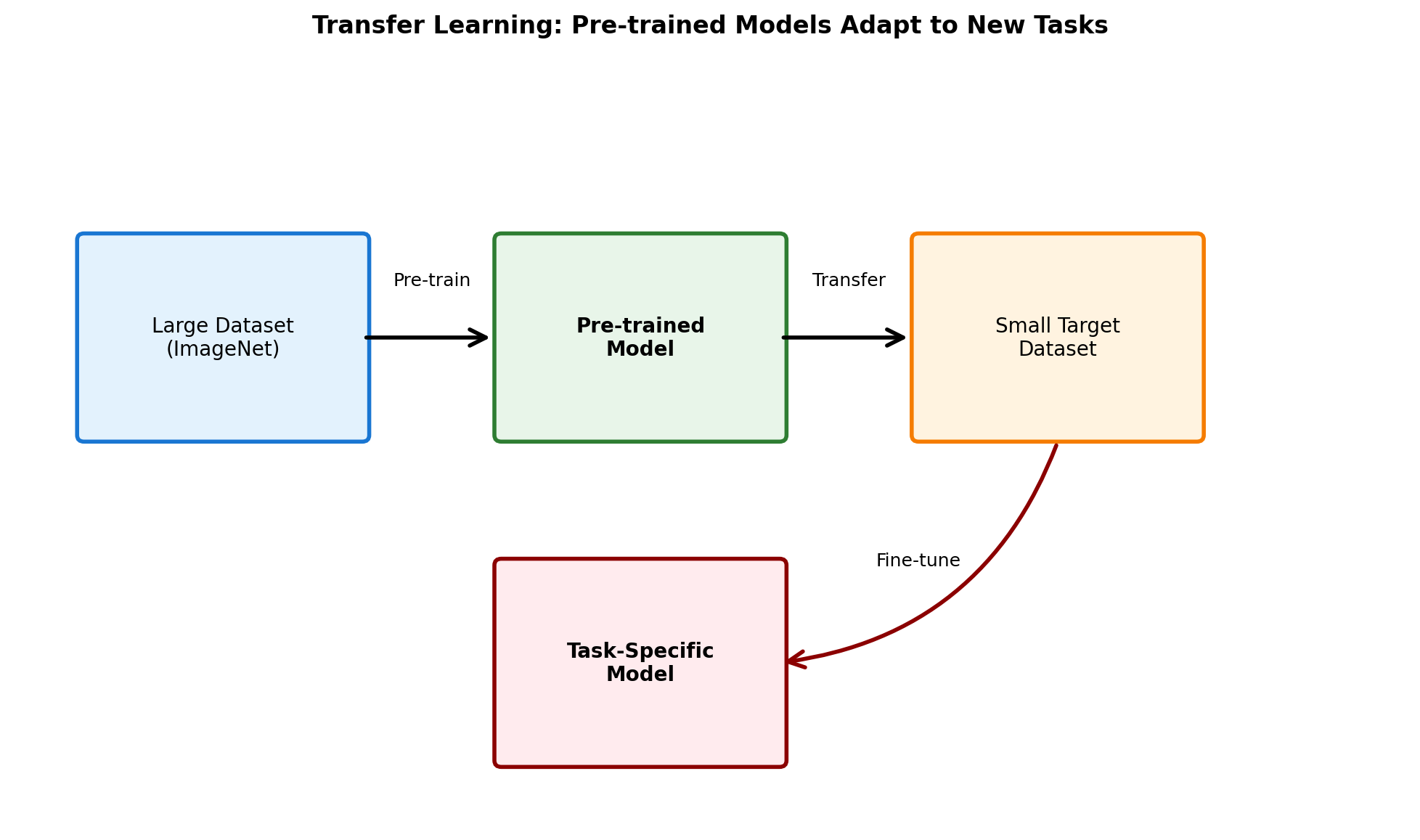
Transfer Learning Pipeline
Hybrid Learning Approaches
Modern approaches often combine paradigms for better performance
Neural Architecture
Neural Networks Form a Rich Hypothesis Class
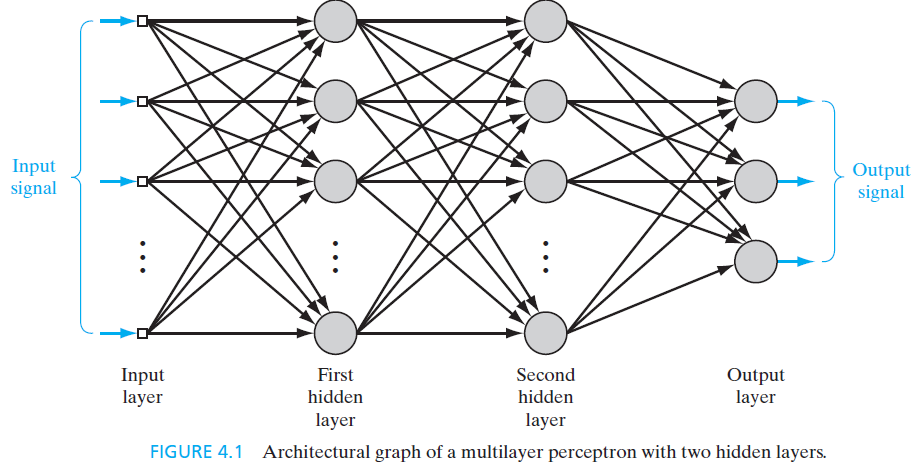
Multilayer Perceptron (MLP): Fully connected feedforward network
Architecture Components
- Input layer: Raw features \(\mathbf{x} \in \mathbb{R}^d\)
- Hidden layers: Learned representations
- Output layer: Task-specific predictions
- Connections: All-to-all between layers
Why “Rich” Hypothesis Class?
- Each neuron: Nonlinear transformation
- Composition: Exponential expressivity
- Universal approximation capability
Defn: Deep Neural Network
A neural network with more than one hidden layer. Depth enables hierarchical feature learning: early layers learn simple features, deeper layers learn complex abstractions.
Single Neuron Computation
Forward Computation
At neuron \(i\) in layer \(l\):
\[a_i^{(l)} = h\left(\left[\mathbf{w}_i^{(l)}\right]^\top \mathbf{a}^{(l-1)} + b_i^{(l)}\right)\]
where:
- \(\mathbf{a}^{(l-1)}\): Previous layer activations
- \(\mathbf{w}_i^{(l)}\): Weight vector for neuron \(i\)
- \(b_i^{(l)}\): Bias term
- \(h(\cdot)\): Activation function
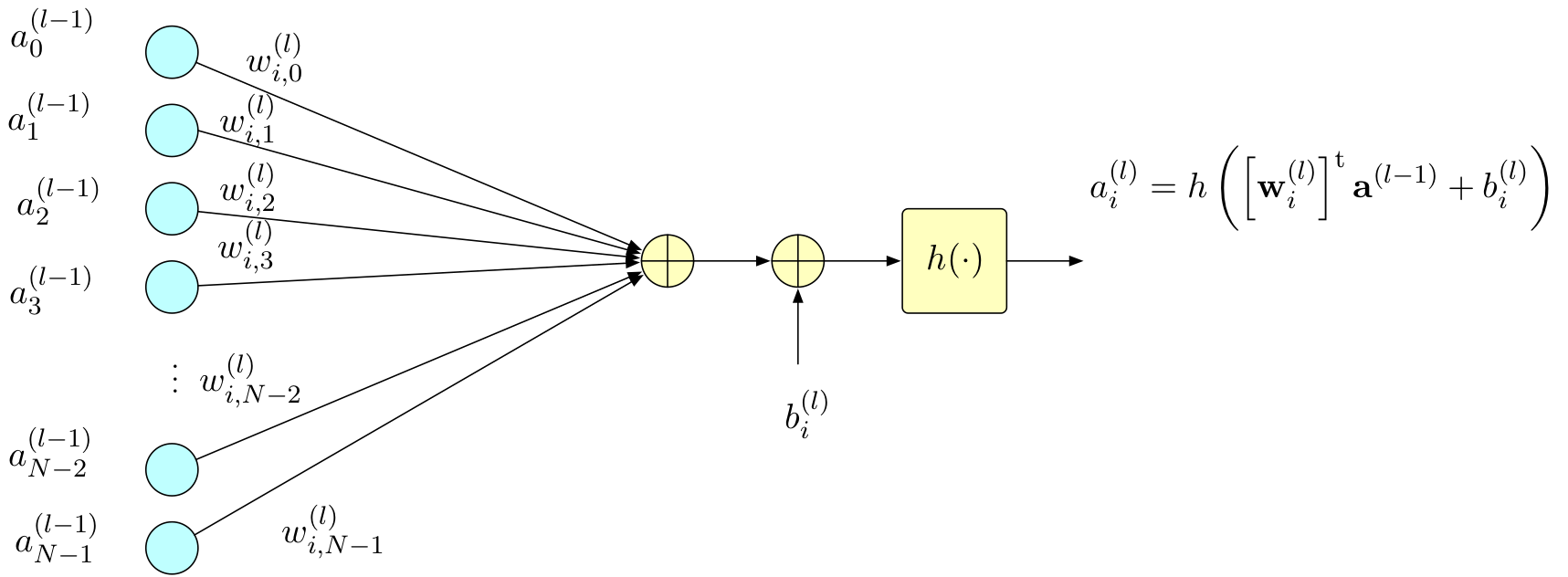
Matrix Form (Entire Layer)
\[\mathbf{a}^{(l)} = h\left(\mathbf{W}^{(l)} \mathbf{a}^{(l-1)} + \mathbf{b}^{(l)}\right)\]
- Parallelizes computation
- Enables GPU acceleration
Universal Approximation: Existence Guarantee
Cybenko (1989), Hornik et al. (1989)
A feedforward network with:
- Single hidden layer
- Finite number of neurons
- Non-polynomial activation
can approximate any continuous function on compact subset of \(\mathbb{R}^n\) to arbitrary accuracy
Critical word: CAN
The theorem guarantees such networks exist. Finding them through training is different.
Preview
Detailed treatment later: approximation theory, width vs depth, practical training implications
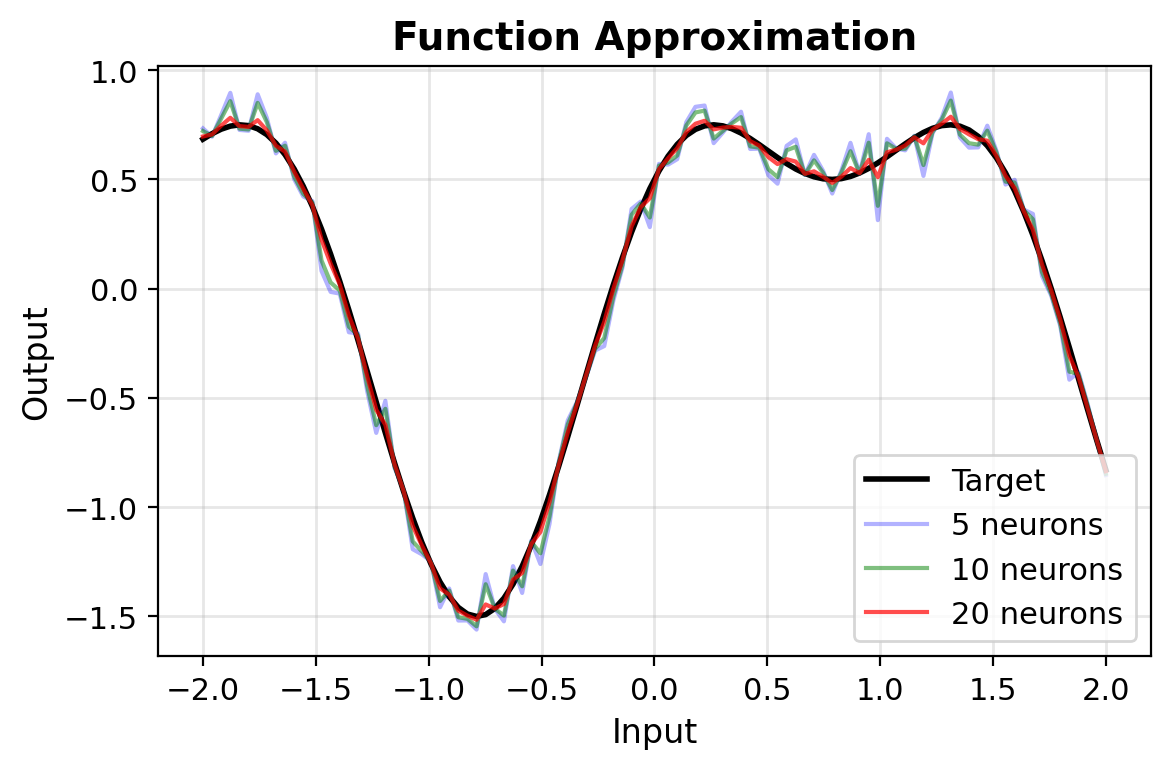
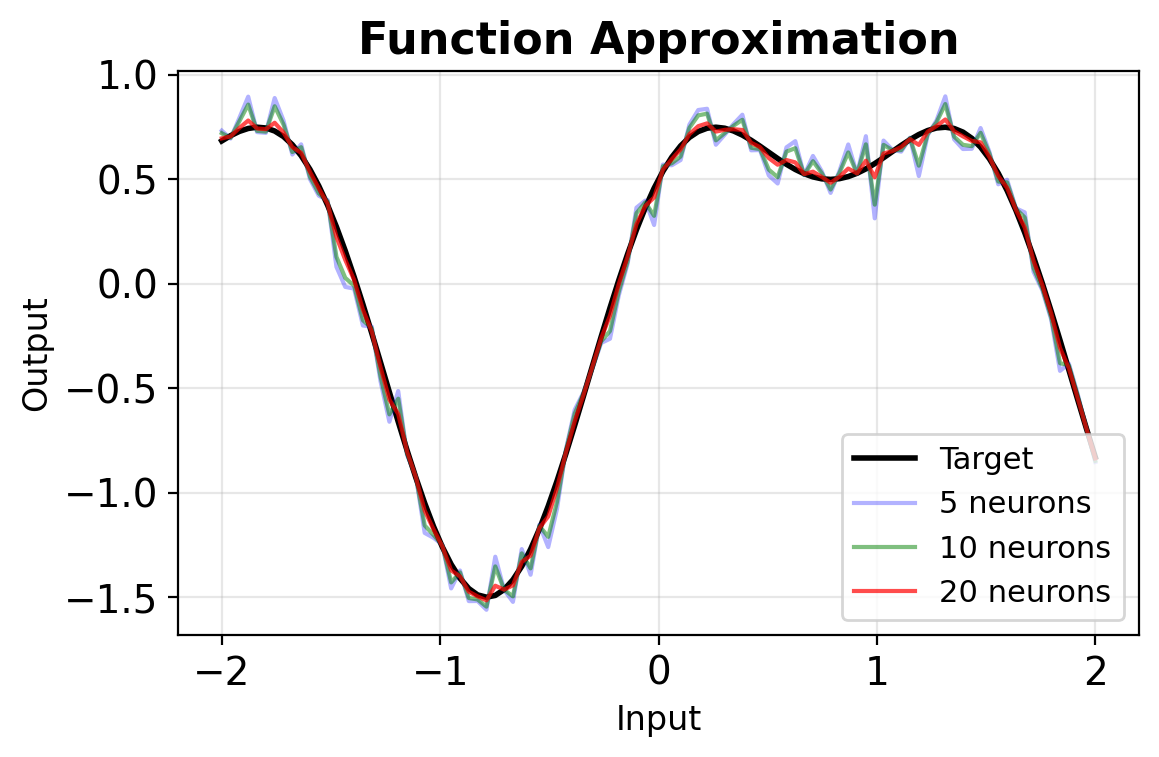
Width vs Depth: Why We Use Deep Networks
Width-only (single hidden layer)
Universal approximation guarantees this works, but:
- May require exponentially many neurons
- Example: parity function on n bits needs \(2^{n-1}\) hidden units
- Theorem says existence, not efficiency
Depth (multiple layers)
- More parameter-efficient representation
- Polynomial neurons vs exponential
- Hierarchical features emerge
- Same expressivity, fewer parameters
Why depth matters: Practical networks need efficient representations
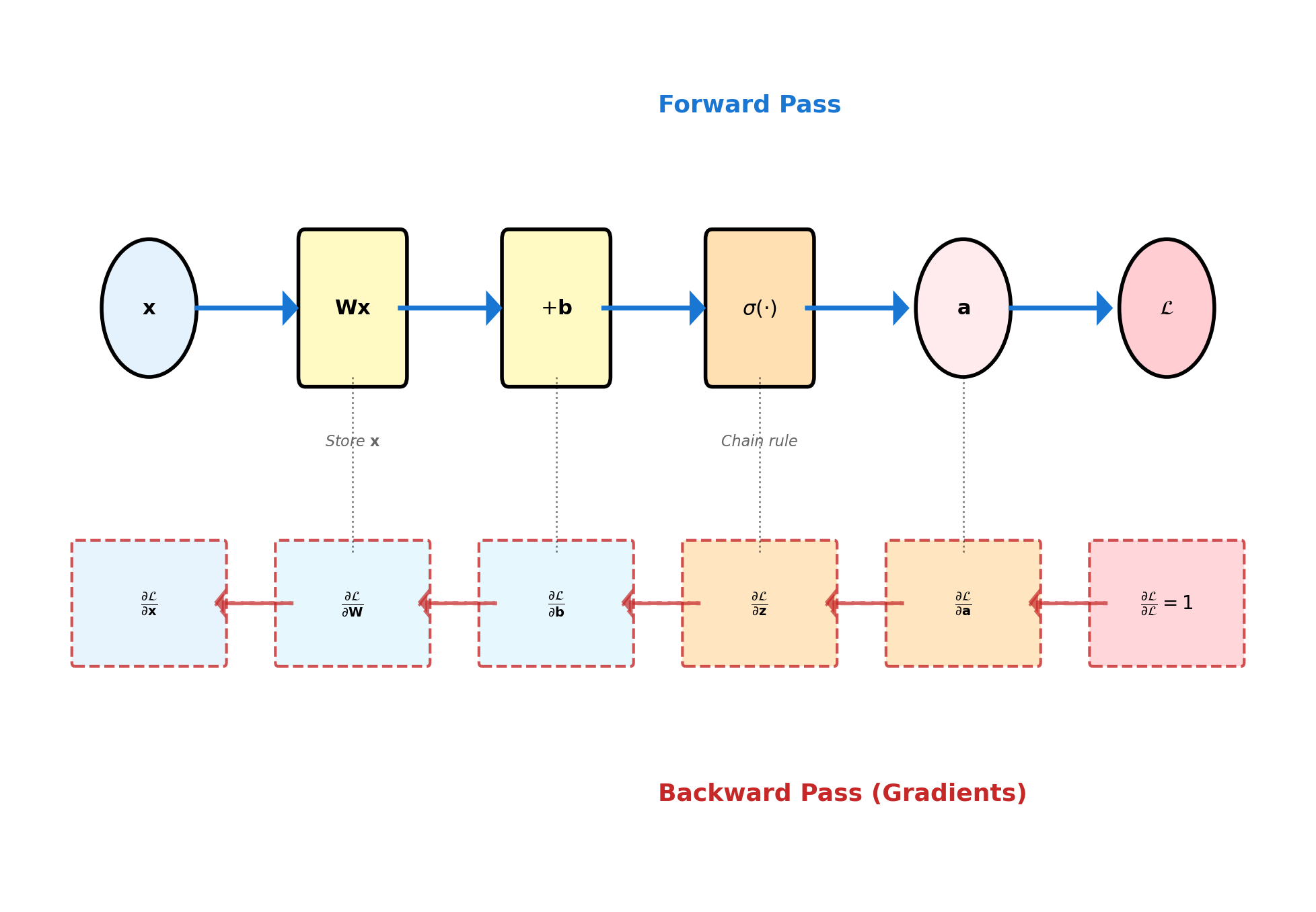
Forward and Backward Pass
Implementation
class Layer:
def forward(self, x):
# Store for backward pass
self.x = x
# Linear transformation
self.z = np.dot(x, self.W) + self.b
# Apply activation
self.a = self.activation(self.z)
return self.a
def backward(self, grad_output):
# Chain rule through activation
grad_z = grad_output * \
self.activation_derivative(self.z)
# Parameter gradients
self.grad_W = np.dot(self.x.T, grad_z)
self.grad_b = np.sum(grad_z, axis=0)
# Input gradient for previous layer
grad_input = np.dot(grad_z, self.W.T)
return grad_inputComputational Graph
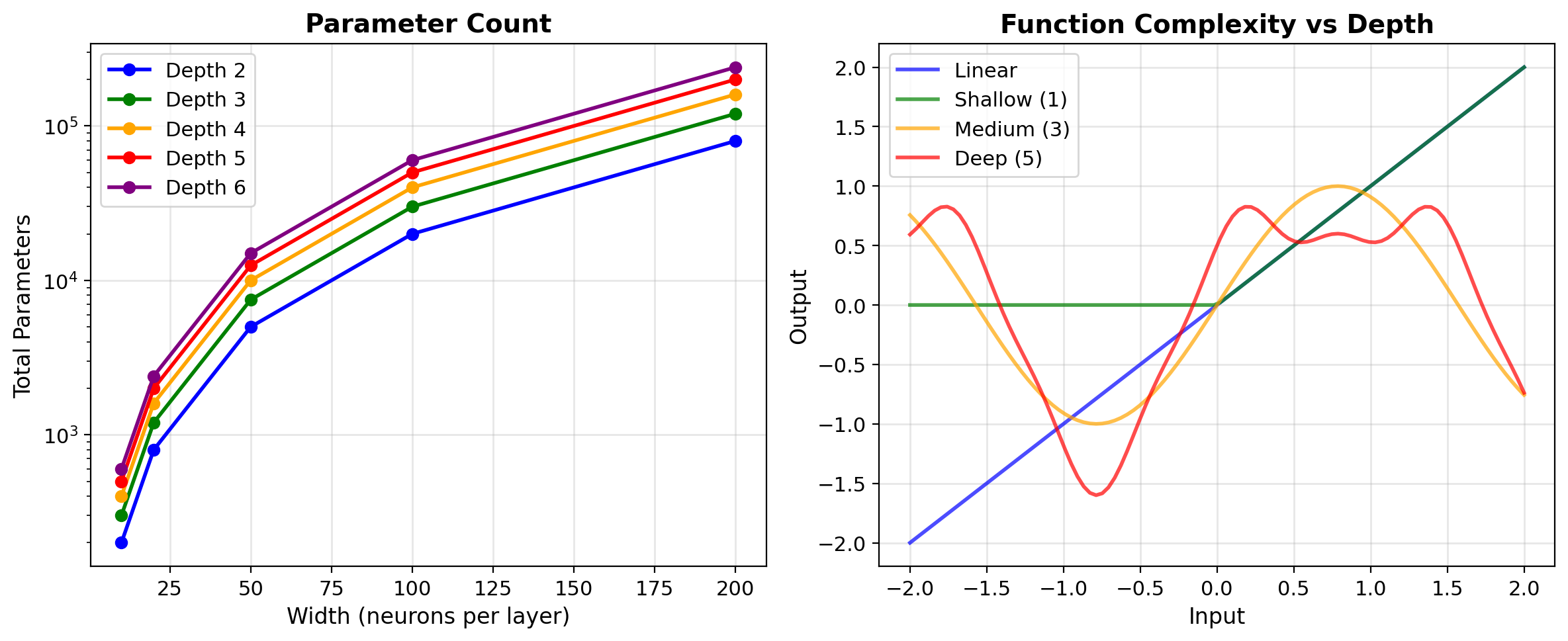
Network Capacity and Depth
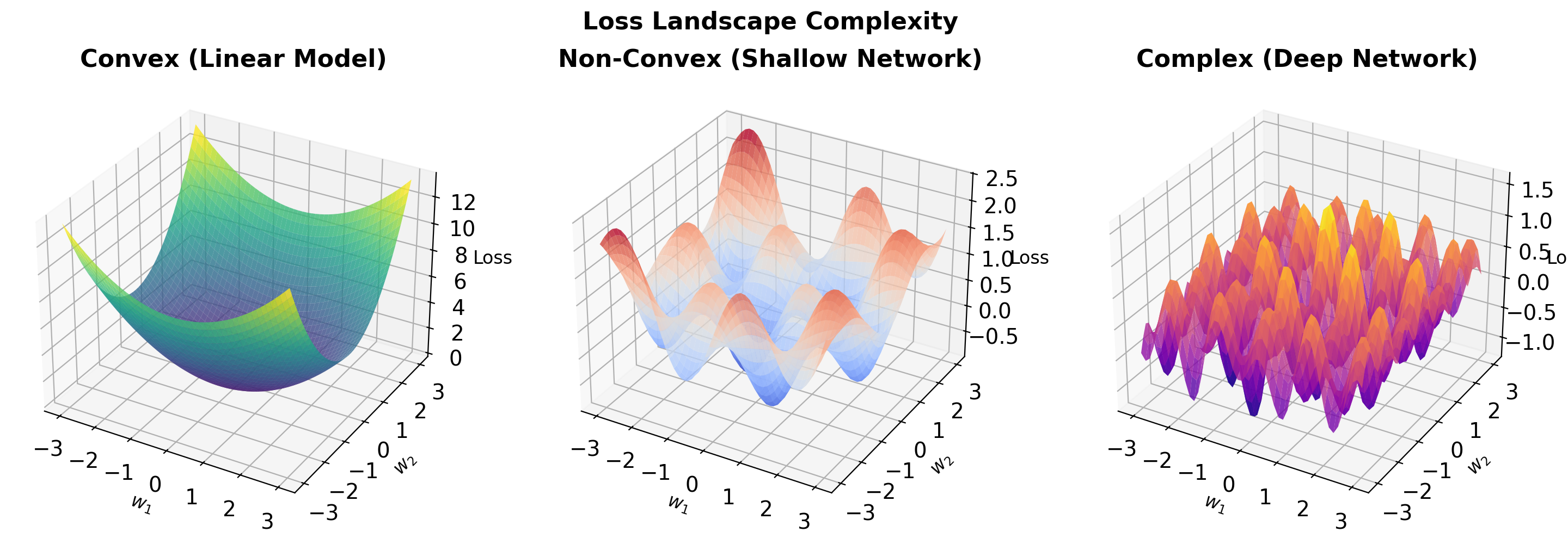
The Optimization Landscape
Loss Surfaces in High Dimensions
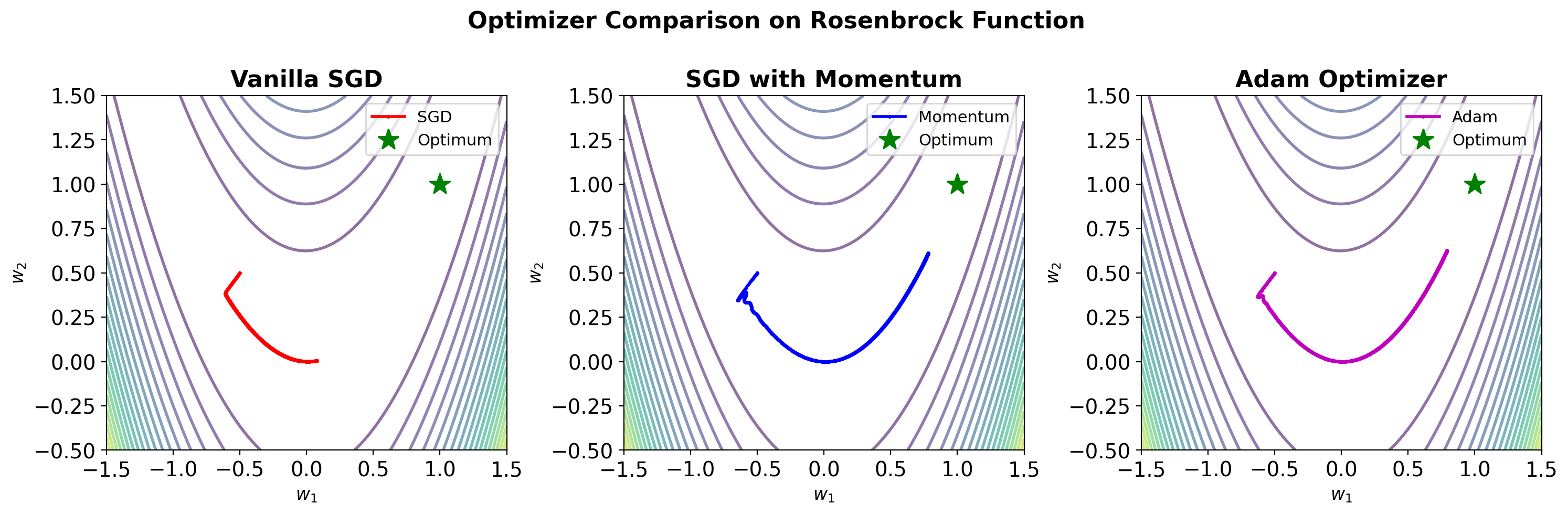
Mathematical Reality
In \(d\) dimensions with \(n\) parameters:
- Critical points: \(\mathcal{O}(e^n)\)
- Most are saddle points, not local minima
- Minima often connected by low-loss paths
Empirical Observations
- Loss landscapes are surprisingly well-behaved
- Wide networks have smoother landscapes
- Overparameterization helps optimization
- Mode connectivity phenomenon
Stochastic Gradient Descent and Variants
Code
def sgd(w, grad, lr=0.01):
return w - lr * grad
def sgd_momentum(w, grad, velocity, lr=0.01, beta=0.9):
velocity = beta * velocity + lr * grad
return w - velocity, velocity
def adam(w, grad, m, v, t, lr=0.001, beta1=0.9, beta2=0.999, eps=1e-8):
m = beta1 * m + (1 - beta1) * grad
v = beta2 * v + (1 - beta2) * grad**2
m_hat = m / (1 - beta1**t)
v_hat = v / (1 - beta2**t)
return w - lr * m_hat / (np.sqrt(v_hat) + eps), m, v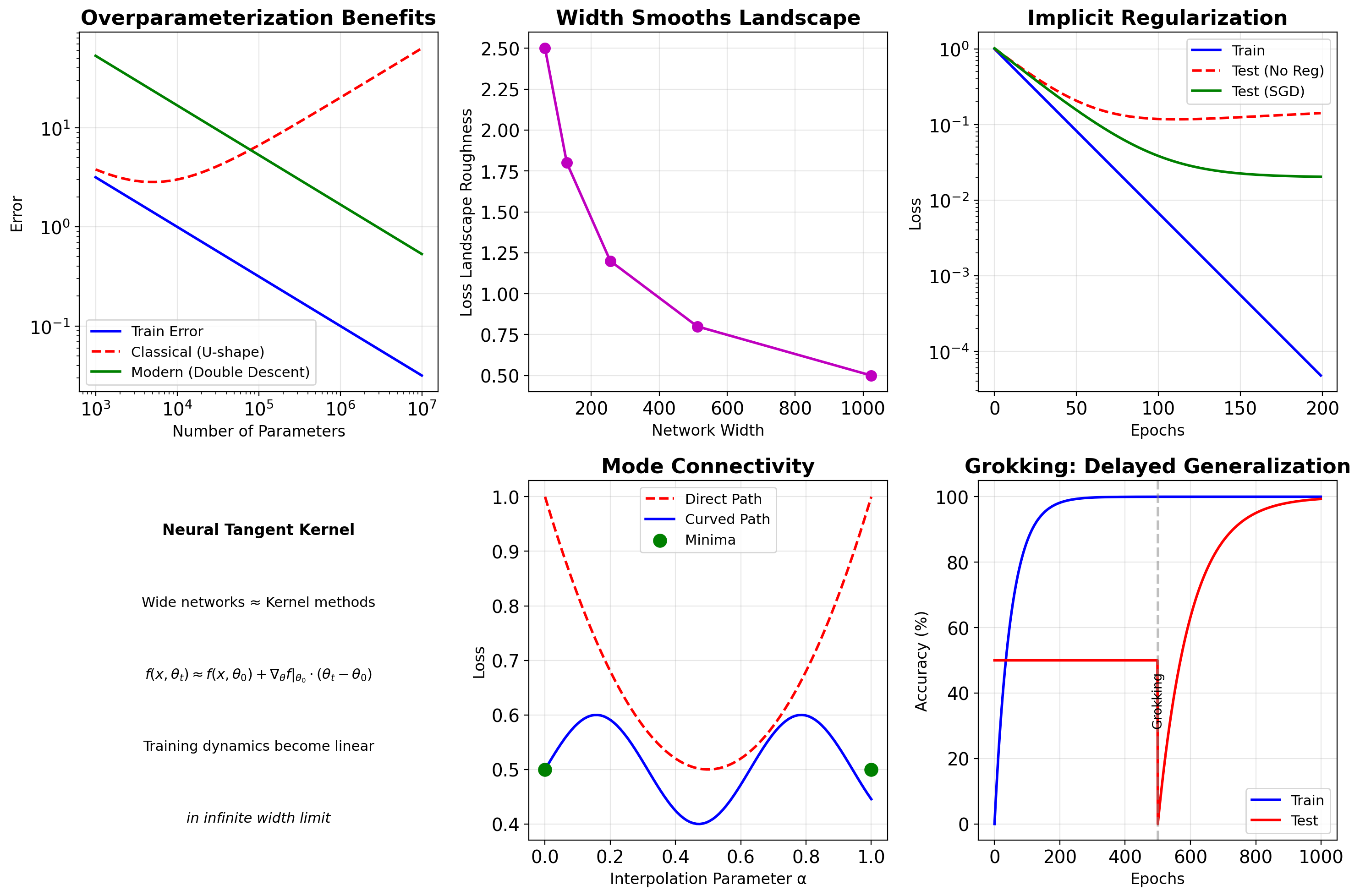
Lottery Ticket Hypothesis: Sparse Subnetworks at Initialization
Frankle & Carbin (2019)
“Dense networks contain sparse subnetworks that can train to comparable accuracy from the same initialization”
Implications
- Networks are vastly overparameterized
- Winning tickets exist at initialization
- Pruning can maintain performance
- Structure matters more than we thought
Practical Impact
\[\text{Parameters: } 100M \to 10M\] \[\text{Performance: } 95\% \to 94.5\%\]
Why this matters:
Storage:
- 100M: ~400MB (too large for mobile)
- 10M: ~40MB (fits on phone)
Speed:
- 100M: ~100ms per image
- 10M: ~10ms per image (real-time)
Training:
- 100M: 5 days on single GPU
- 10M: 12 hours (faster experiments)
Detailed treatment: Network pruning and efficient architectures
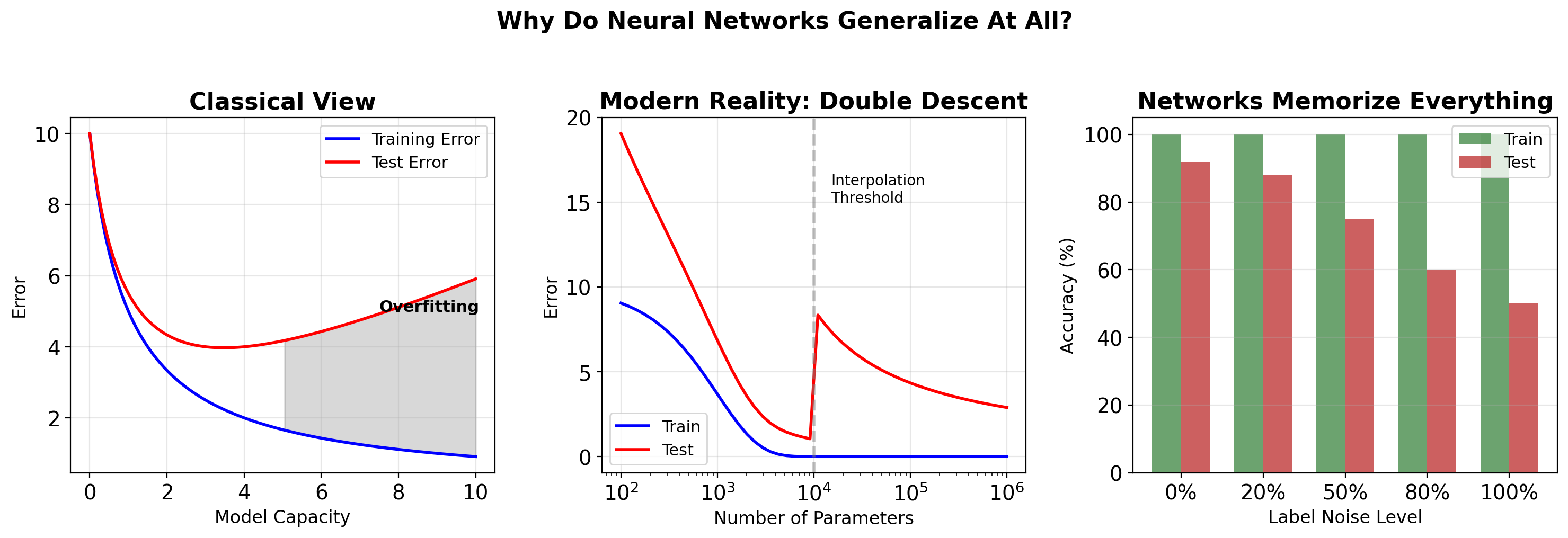
Modern Theoretical Insights
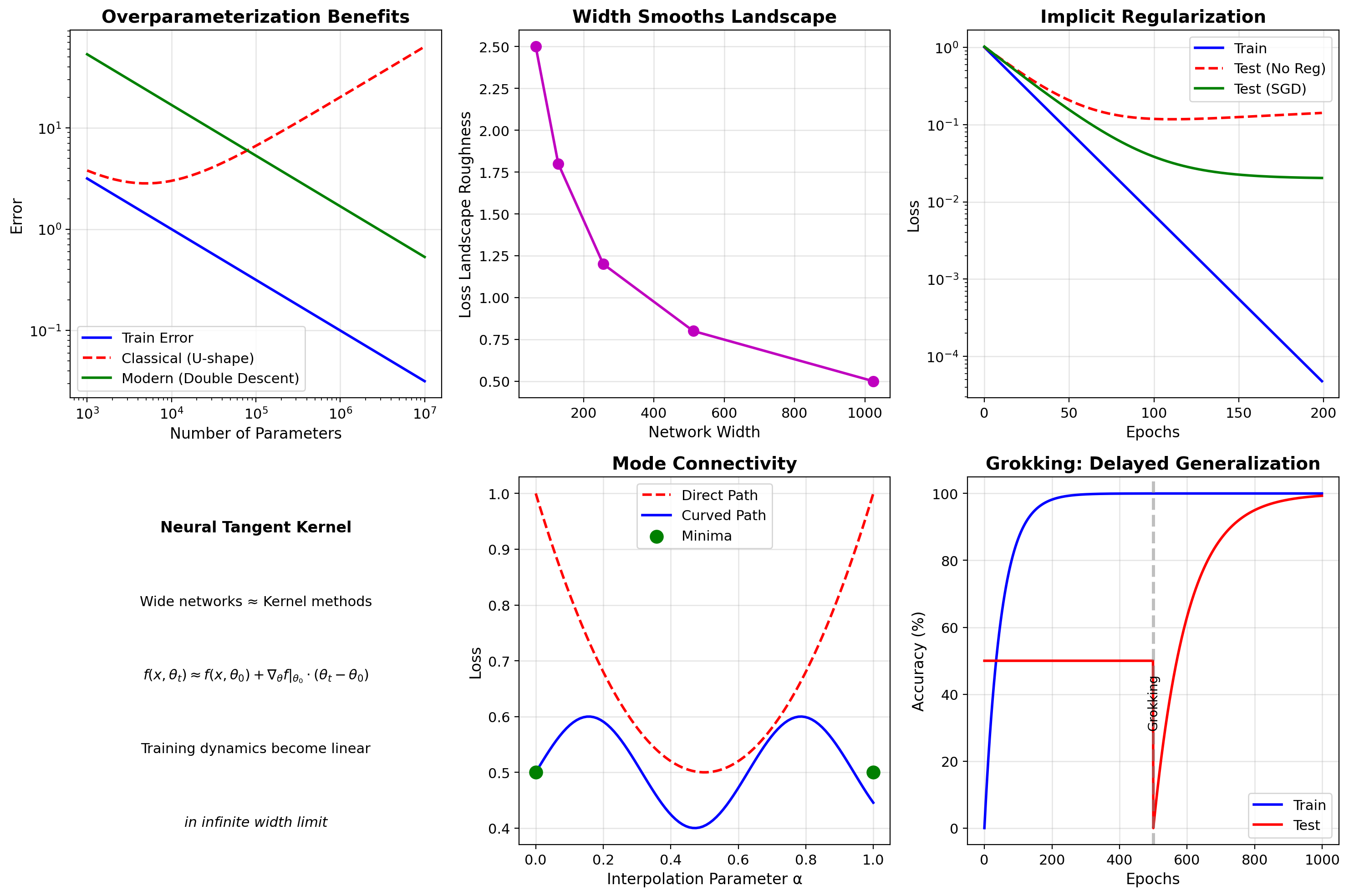
Why Deep Networks Generalize
Neural Networks Memorize Random Labels Yet Generalize on Real Data
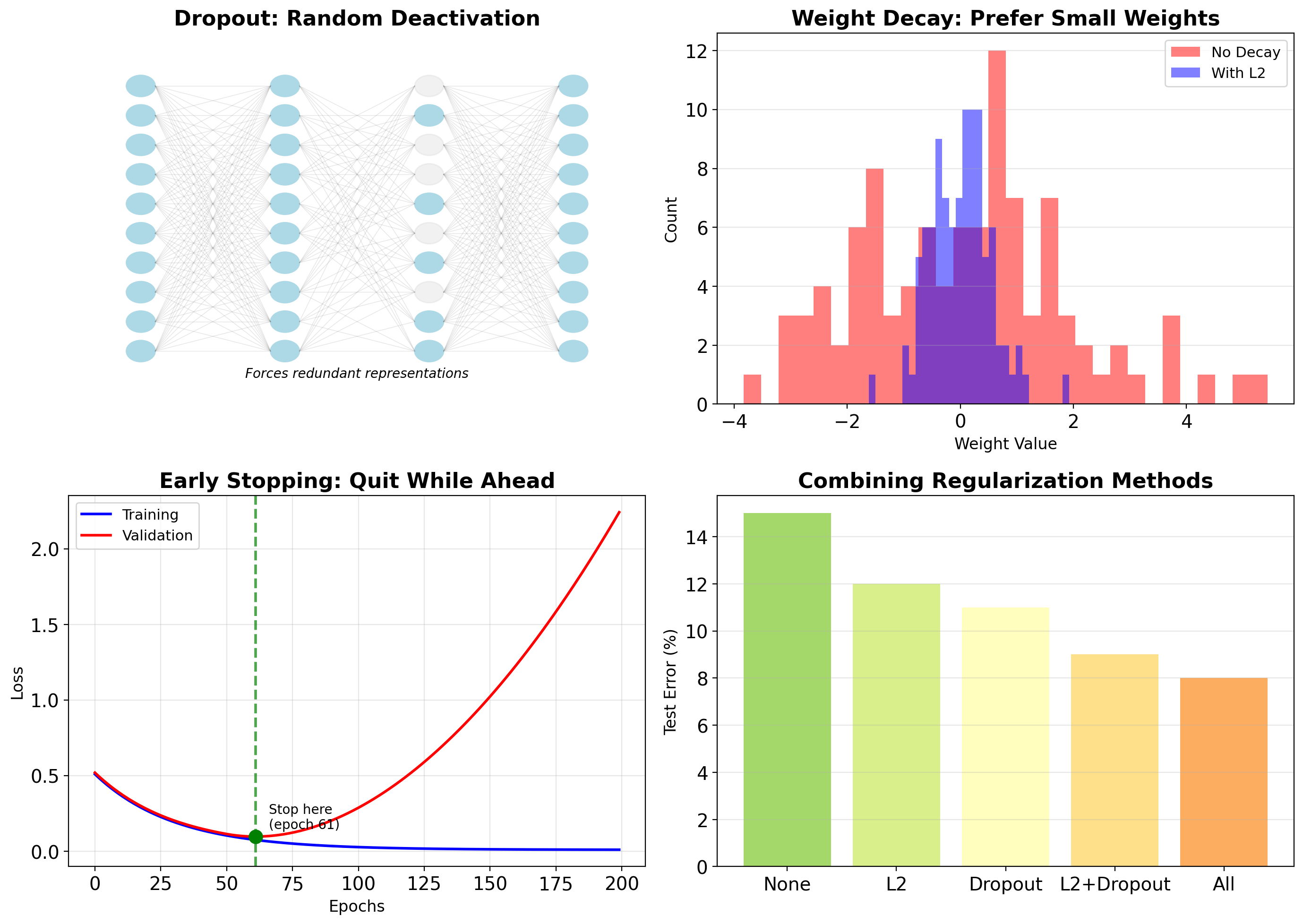
Regularization Techniques: Dropout and Weight Decay
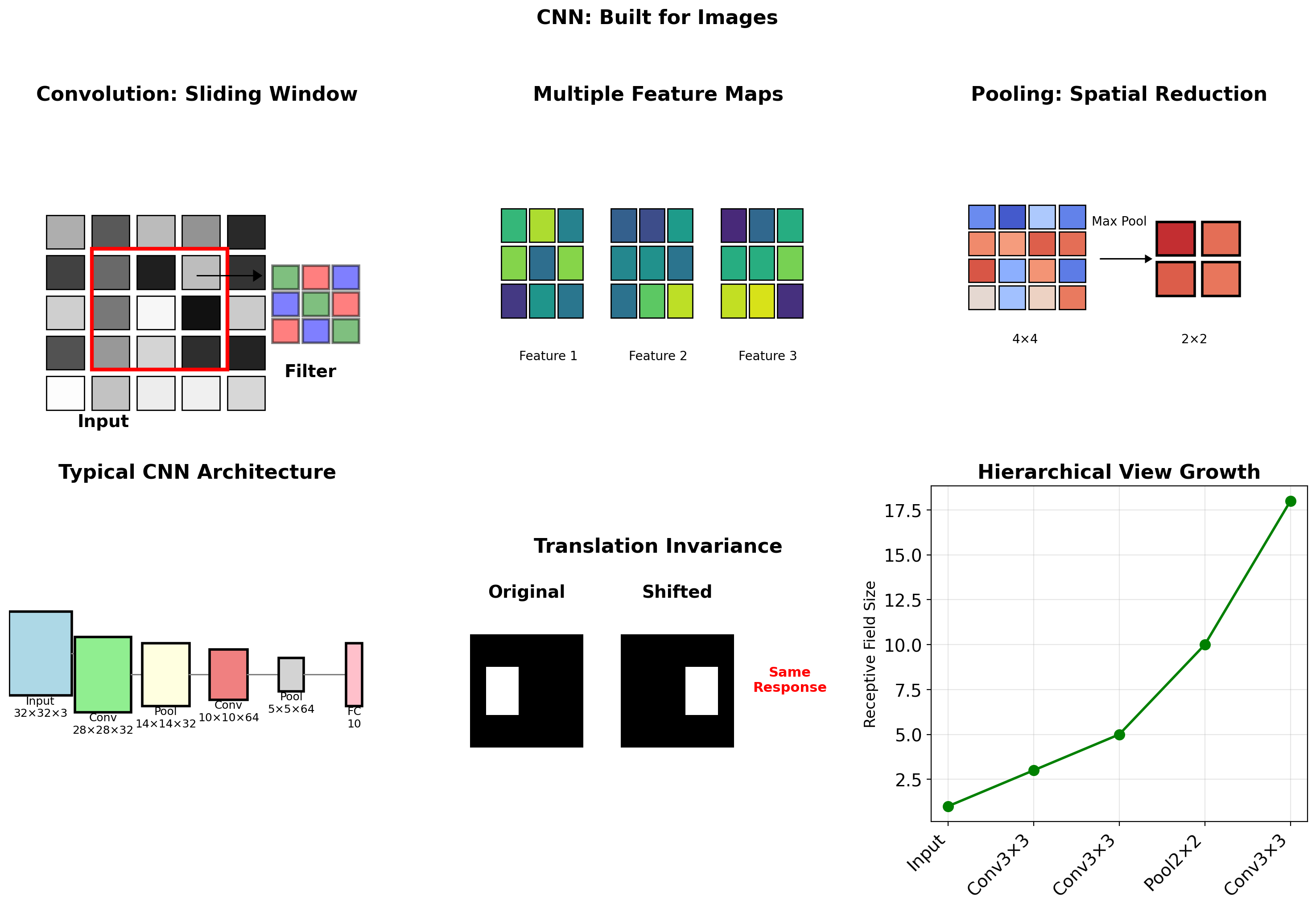
Architecture Embeds Domain Knowledge
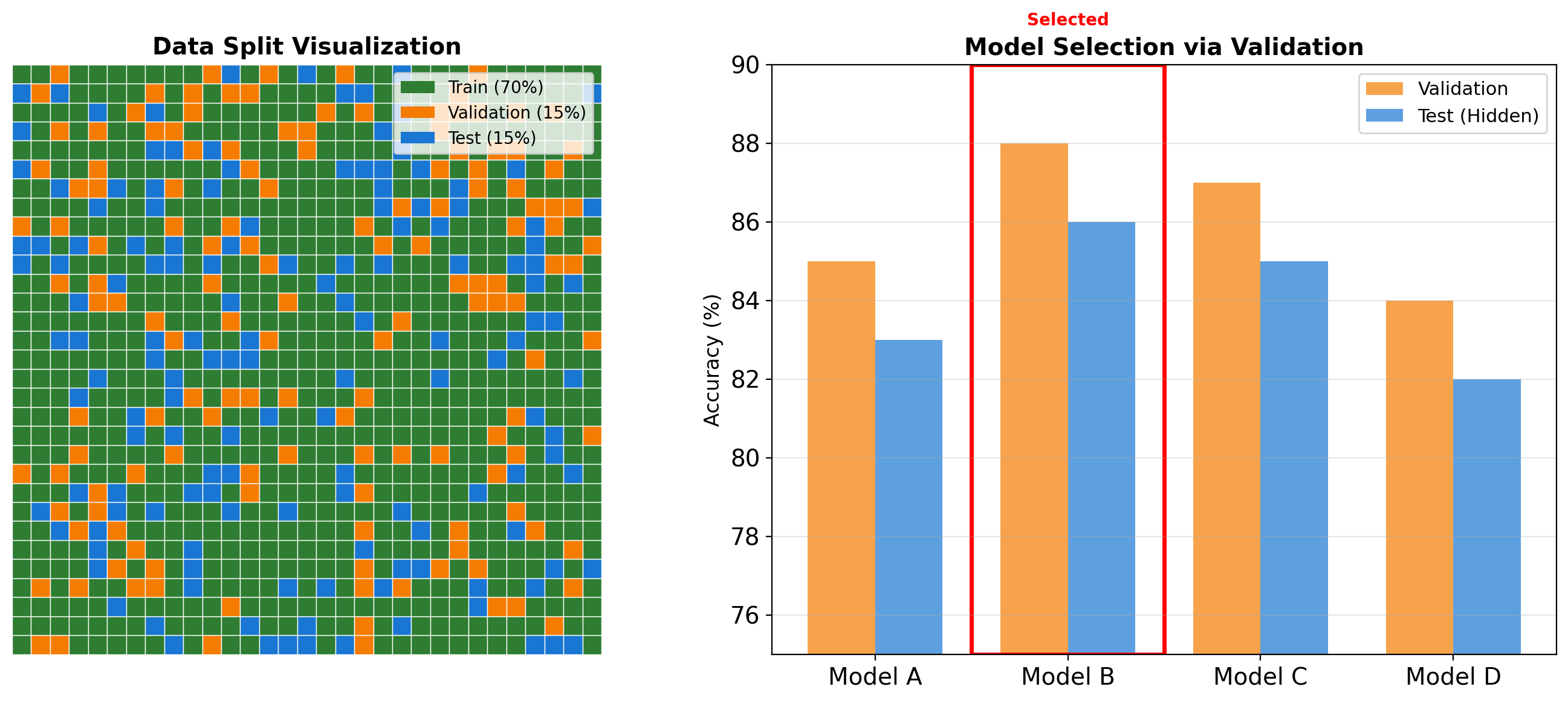
Train/Validation/Test: Sacred Separation
WARNING: Data Contamination
Never touch test data until final evaluation - validation data guides all decisions
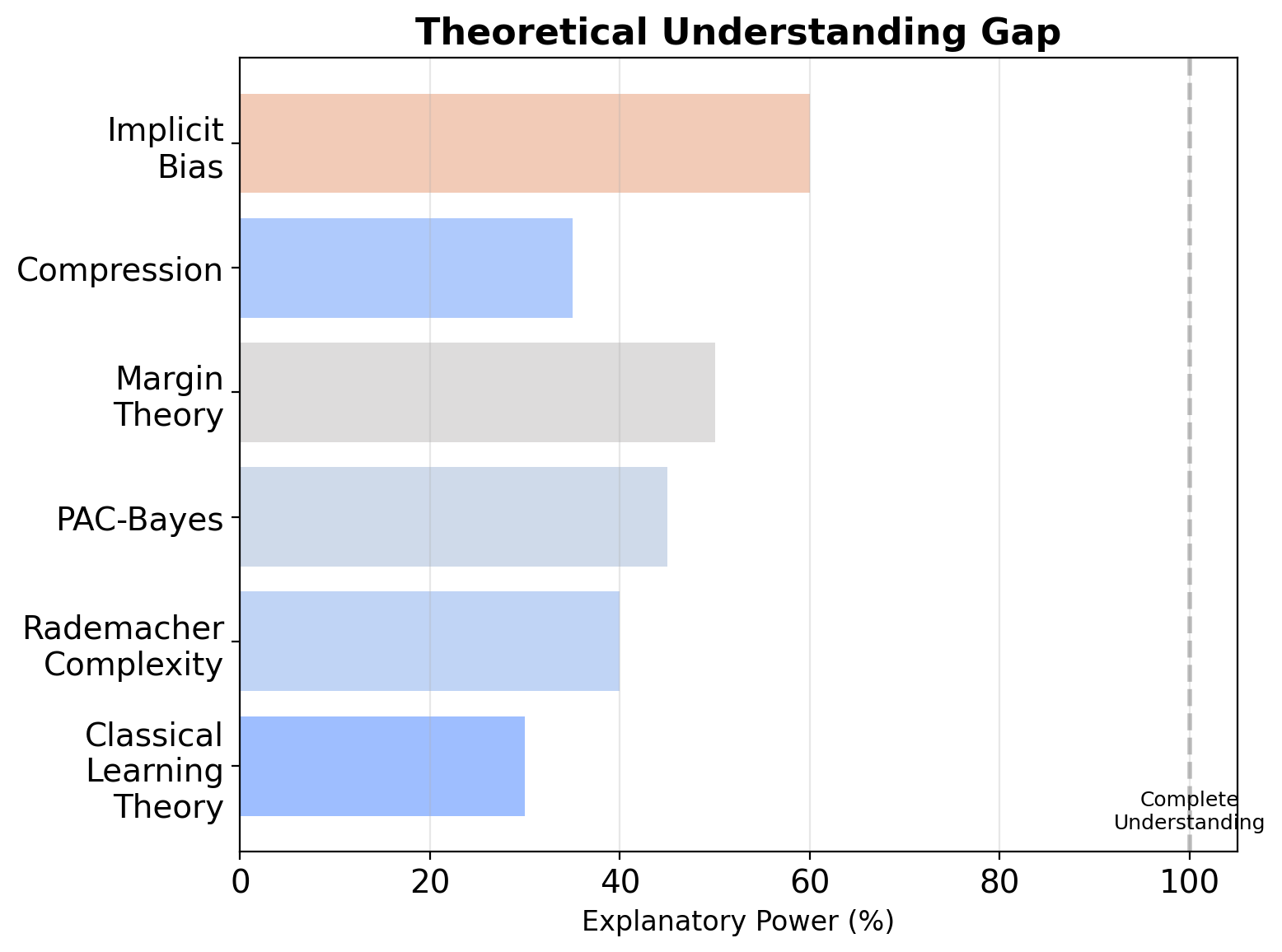
Generalization Remains Partially Unexplained
What We Don’t Understand
Why does SGD find generalizing solutions?
Networks can memorize random labels perfectly,
yet SGD finds patterns when labels are real
Why does overparameterization help?
10x more parameters than samples should overfit,
but often improves test accuracy
What is the role of depth?
Shallow wide networks have same capacity,
but deep networks generalize better
How do transformers generalize?
No convolutions, no recurrence,
yet state-of-the-art on vision and language
Note: No single theory fully explains deep learning generalization. Active research area.
Zillow Home Pricing: When the World Changes
Setup (2018-2021):
- Predict home values for algorithmic buying
- Train on 2018-2020 housing data
- Validation: 95% accurate (within 5% of price)
- Test set: 94% accurate
- Model looked excellent
Deployment (2021):
- COVID shifts housing market
- Model systematically underpredicts by $80K-$100K
- Loss: $500M+ before shutting down
What happened:
Training data came from stable market. Deployment happened during rapid market shift. Model kept predicting pre-COVID prices.
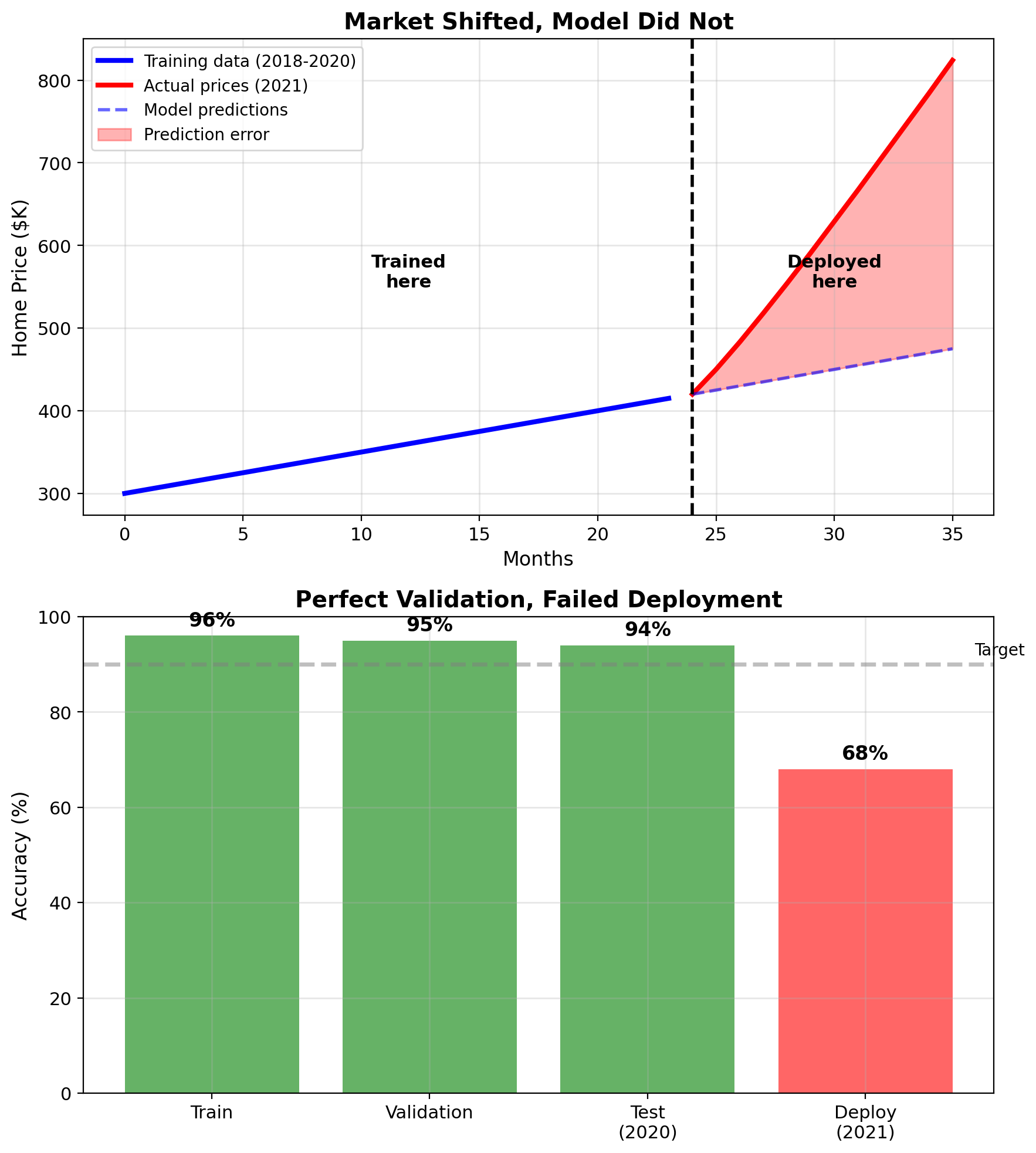
The problem:
All your validation tools assume the future looks like the past. When the world changes, models trained on historical data fail.
Train/val/test all from 2018-2020: Model learns pre-COVID patterns
Deploy in 2021: COVID changed everything
Result: Model is wrong, but doesn't know it's wrongThis is not a rare edge case - markets shift, user behavior changes, new products emerge. Distribution shift is common.
Building Systems Despite Incomplete Theory
What theory doesn’t fully explain
- Why SGD finds generalizing solutions (not just any minimum)
- How overparameterization helps (contradicts classical theory)
- What depth contributes beyond expressivity
- Why some architectures work better than others
Classical theory predicts
- More parameters than data causes overfitting
- Zero training error means poor generalization
- Simpler models should always win
Modern practice shows
- Overparameterized networks generalize well
- Zero training loss often gives best test performance
- Complex models frequently outperform simple ones
How we build systems anyway
Empirical validation:
- Train/validation/test splits (always)
- Monitor generalization gap continuously
- Trust validation performance over theory
Defensive engineering:
- Start simple, add complexity gradually
- Regularize by default (dropout, weight decay)
- Early stopping when validation degrades
- Ensemble multiple models for robustness
Course approach:
- Learn techniques that work empirically
- Understand intuition for why they might work
- Recognize when theory provides guarantees
- Know when you’re operating without guarantees
Many fundamental questions remain open research problems.
Modern Deep Architectures
Convolutional Networks: Exploiting Spatial Structure
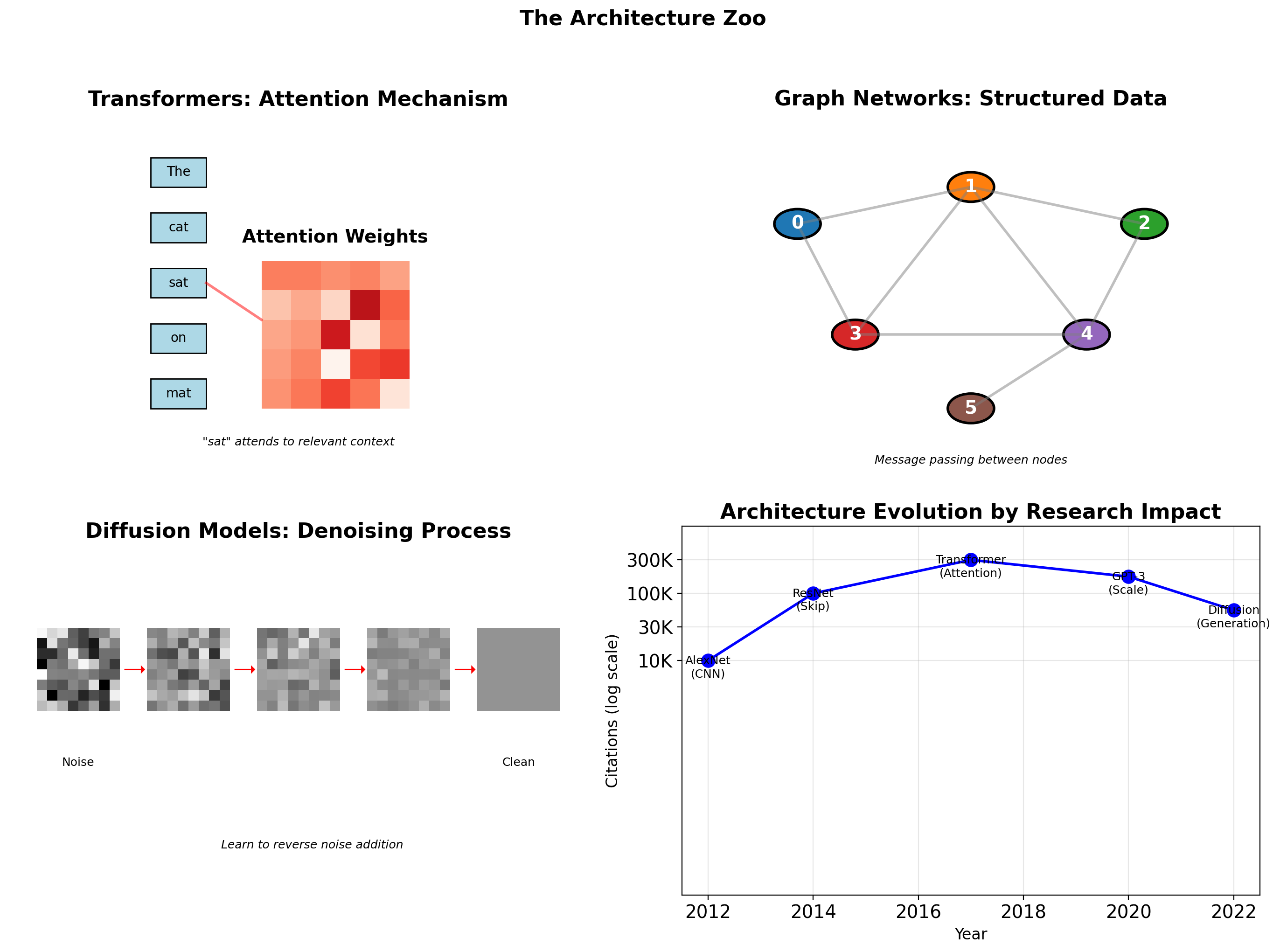
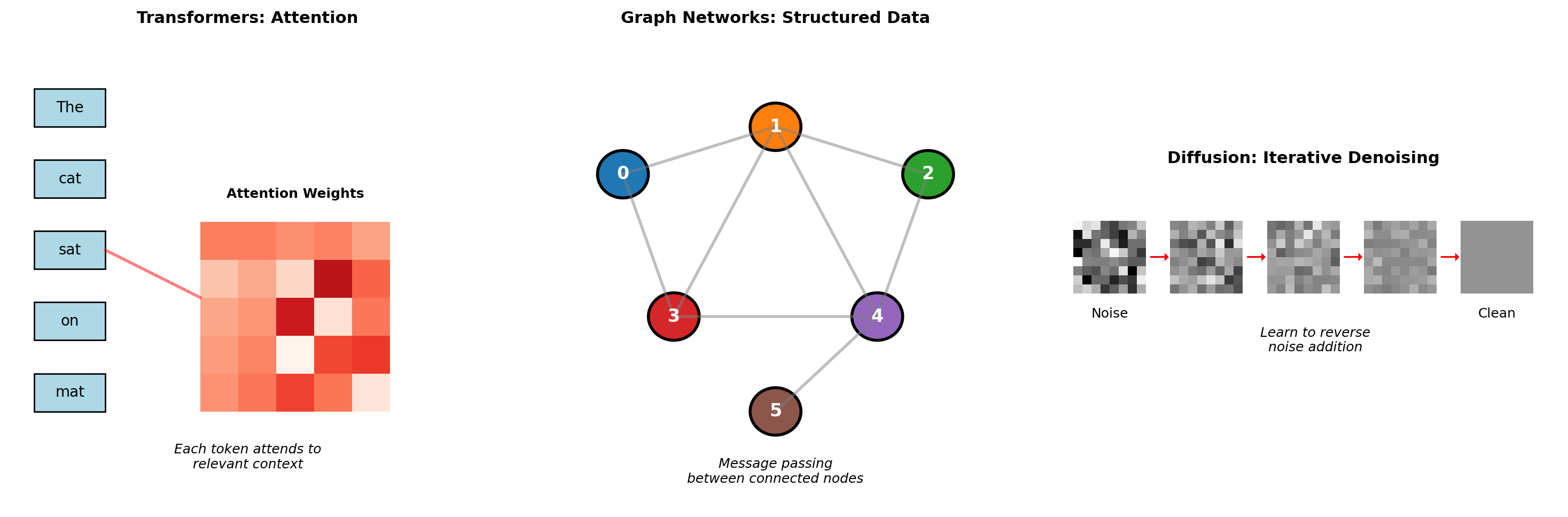
Preview: Transformers, Graph Networks, and Diffusion Models
Building a Simple CNN
import numpy as np
class Conv2D:
def __init__(self, in_channels, out_channels, kernel_size=3):
self.in_channels = in_channels
self.out_channels = out_channels
self.kernel_size = kernel_size
# Initialize filters
self.filters = np.random.randn(
out_channels, in_channels, kernel_size, kernel_size
) * 0.1
self.bias = np.zeros(out_channels)
def forward(self, x):
batch, in_c, height, width = x.shape
out_h = height - self.kernel_size + 1
out_w = width - self.kernel_size + 1
output = np.zeros((batch, self.out_channels, out_h, out_w))
# Convolution operation
for b in range(batch):
for oc in range(self.out_channels):
for h in range(out_h):
for w in range(out_w):
# Extract patch
patch = x[b, :, h:h+self.kernel_size, w:w+self.kernel_size]
# Convolve with filter
output[b, oc, h, w] = np.sum(patch * self.filters[oc]) + self.bias[oc]
return output
class MaxPool2D:
def __init__(self, pool_size=2):
self.pool_size = pool_size
def forward(self, x):
batch, channels, height, width = x.shape
out_h = height // self.pool_size
out_w = width // self.pool_size
output = np.zeros((batch, channels, out_h, out_w))
for h in range(out_h):
for w in range(out_w):
h_start = h * self.pool_size
w_start = w * self.pool_size
pool_region = x[:, :, h_start:h_start+self.pool_size,
w_start:w_start+self.pool_size]
output[:, :, h, w] = np.max(pool_region, axis=(2, 3))
return output
# Example usage
x = np.random.randn(1, 3, 32, 32) # Batch=1, RGB, 32x32
conv = Conv2D(3, 16, kernel_size=3)
pool = MaxPool2D(pool_size=2)
x = conv.forward(x)
print(f"After conv: {x.shape}") # (1, 16, 30, 30)
x = np.maximum(0, x) # ReLU
x = pool.forward(x)
print(f"After pool: {x.shape}") # (1, 16, 15, 15)After conv: (1, 16, 30, 30)
After pool: (1, 16, 15, 15)Architecture Efficiency on ImageNet
ResNet-50 (2015):
- 25M parameters
- 76% top-1 accuracy
- 10ms inference (GPU)
MobileNetV2 (2018):
- 3.5M parameters (7× smaller)
- 72% top-1 accuracy (4% drop)
- 3ms inference (3× faster)
EfficientNet-B0 (2019):
- 5M parameters (5× smaller than ResNet)
- 77% top-1 accuracy (1% higher than ResNet)
- 4ms inference (2.5× faster)
Architecture design matters: EfficientNet achieves better accuracy than ResNet-50 with far fewer parameters.
The Practice of Deep Learning
A Recipe for Training Neural Networks
The Training Loop
\[\theta_{t+1} = \theta_t - \eta \cdot \frac{1}{|B|} \sum_{i \in B} \nabla_\theta \mathcal{L}(f_\theta(x_i), y_i)\]
Karpathy’s Principles
1. Become one with the data Look at your data. Plot it. Understand its distribution, outliers, patterns.
2. Set up end-to-end pipeline Get a simple model training before complexity.
3. Overfit a single batch If you can’t overfit 10 examples, something is broken.
4. Verify loss at initialization Check loss matches expected value (e.g., \(\log(n_{classes})\) for classification).
5. Add complexity gradually Start simple, add one thing at a time.
# The debugging progression
def debug_training():
# Step 1: Overfit one example
single_x = X[0:1]
single_y = y[0:1]
for _ in range(100):
loss = train_step(single_x, single_y)
assert loss < 0.01, "Can't overfit single"
# Step 2: Overfit small batch
batch_x = X[0:10]
batch_y = y[0:10]
for _ in range(500):
loss = train_step(batch_x, batch_y)
assert loss < 0.1, "Can't overfit batch"
# Step 3: Check with real data
# Only now move to full dataset
return "Ready for full training"Debugging Deep Learning
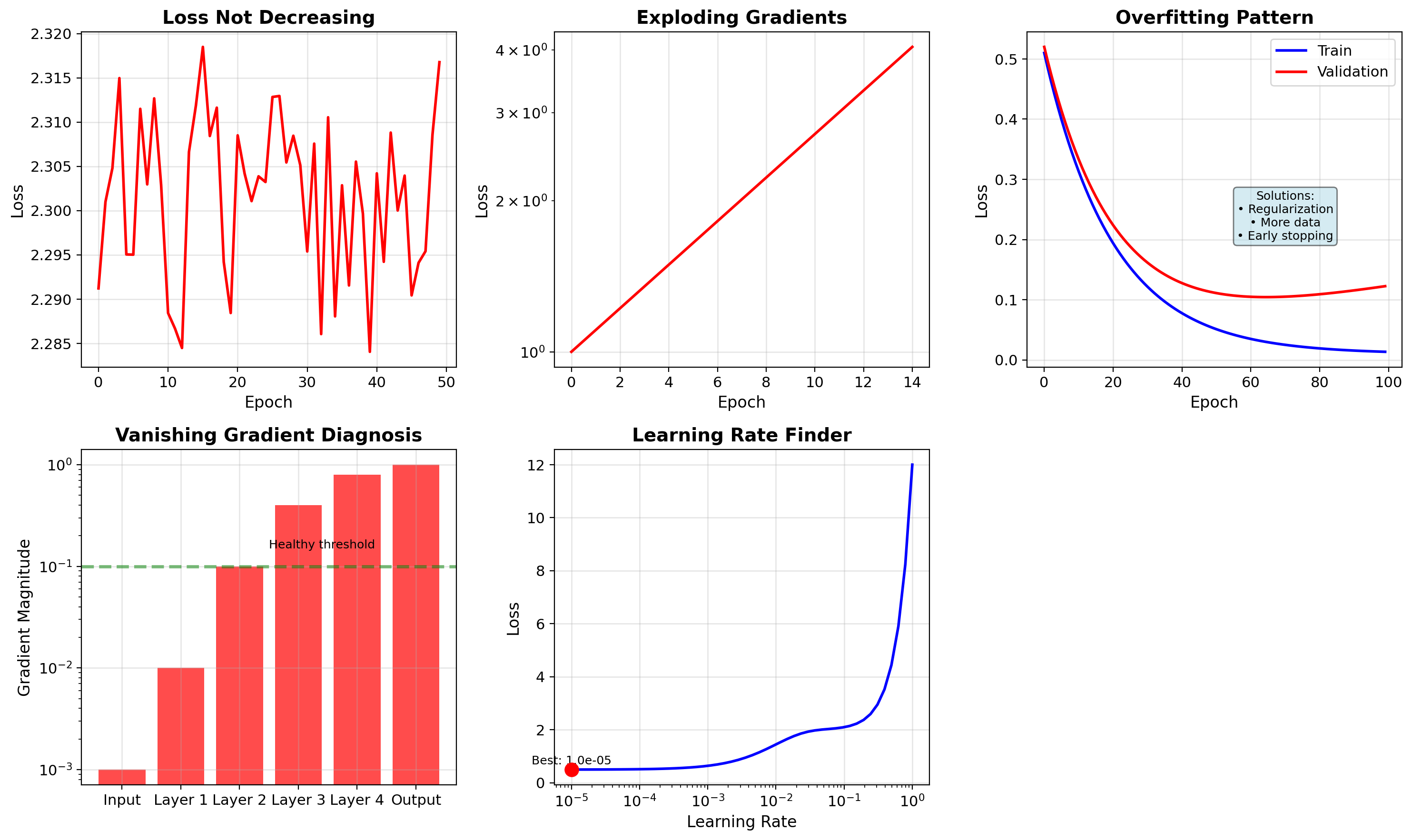
Medical Imaging: High Accuracy Hides Dataset Problems
Setup:
- Train pneumonia detector on chest X-rays
- Dataset: 10,000 images from Hospital A
- Training accuracy: 95%
- Validation accuracy: 94%
- Model looks ready to deploy
Deployment at Hospital B:
- Accuracy drops to 72%
- False negatives increase 3×
What went wrong:
Hospital A used one X-ray machine model with specific image characteristics. Hospital B used different equipment. Model learned machine artifacts, not disease patterns.
Example artifacts learned:
- Brightness/contrast settings
- Image resolution differences
- Metal markers in specific corners
- Patient positioning conventions
Shortcut learning: Standard debugging looked fine:
- Training loss decreasing smoothly
- No overfitting (train/val gap small)
- High validation accuracy
- Good precision/recall on test set
Problem only appeared on different hospital equipment. Models exploit spurious correlations (disease + specific machine) as shortcuts instead of learning actual medical patterns.
Computational Realities
What this means for this course:
CPU (your laptop):
- Sufficient for: Most course assignments including smaller CNNs
- Time scale: Minutes per epoch on MNIST, tens of minutes on CIFAR-10
- Cost: Free
GPU (Colab/Kaggle free tier):
- Useful for: Faster iteration, larger architectures, final project
- Time scale: Seconds per epoch
- Cost: Free (with session limits)
Multi-GPU (cloud):
- Rarely needed: Only for very large-scale experiments
- Cost: $1-3 per hour
Course approach: CPU is viable for most work. GPU accelerates but isn’t required.
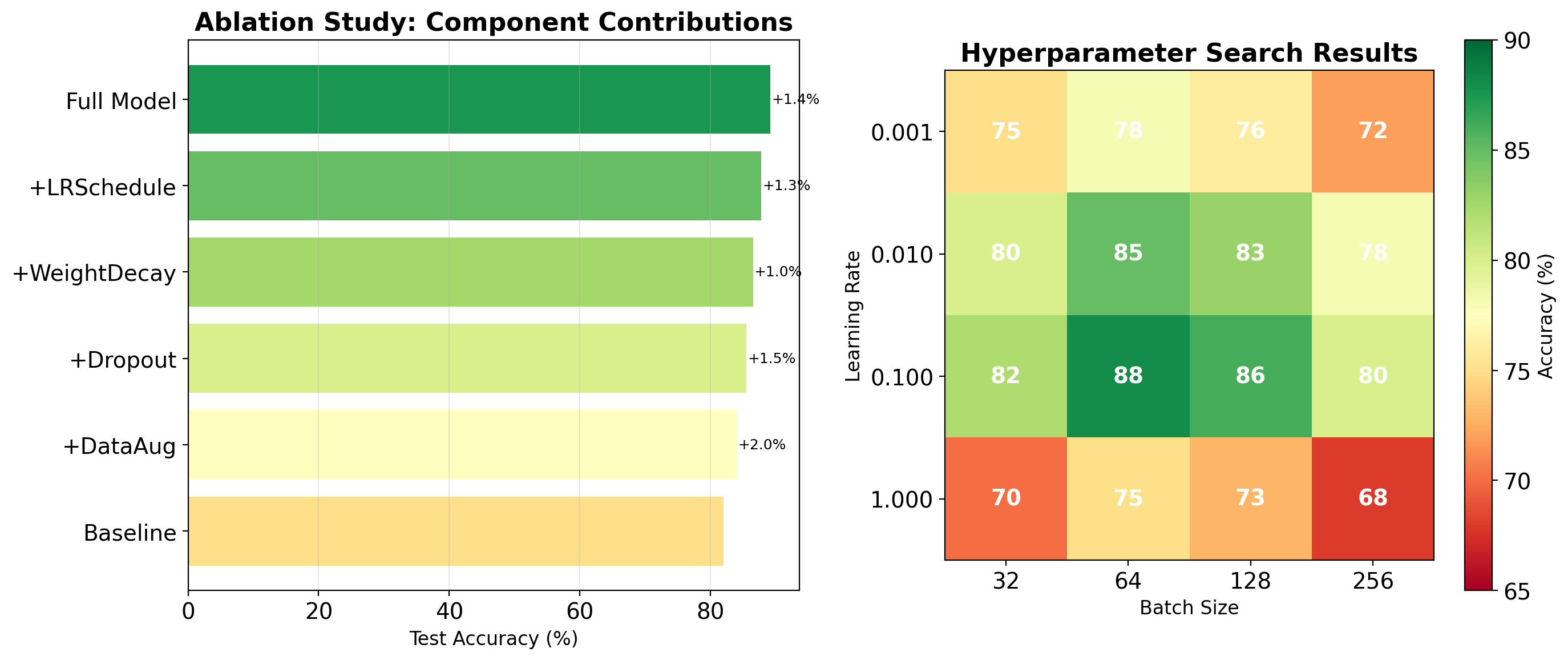
Systematic Experimentation
Experiment tracking example
# Tracking experiments
experiment_config = {
'model': 'resnet18',
'dataset': 'cifar10',
'batch_size': 128,
'lr': 0.1,
'epochs': 100,
'seed': 42,
'timestamp': '2025-01-15-14:30'
}
# Always set seeds for reproducibility
def set_all_seeds(seed=42):
np.random.seed(seed)
# torch.manual_seed(seed)
# torch.cuda.manual_seed_all(seed)
# random.seed(seed)
# Log everything
def log_metrics(epoch, train_loss, val_loss, val_acc):
metrics = {
'epoch': epoch,
'train_loss': train_loss,
'val_loss': val_loss,
'val_acc': val_acc,
'lr': get_current_lr(),
'timestamp': time.time()
}
# Write to file, tensorboard, wandb, etc.
return metrics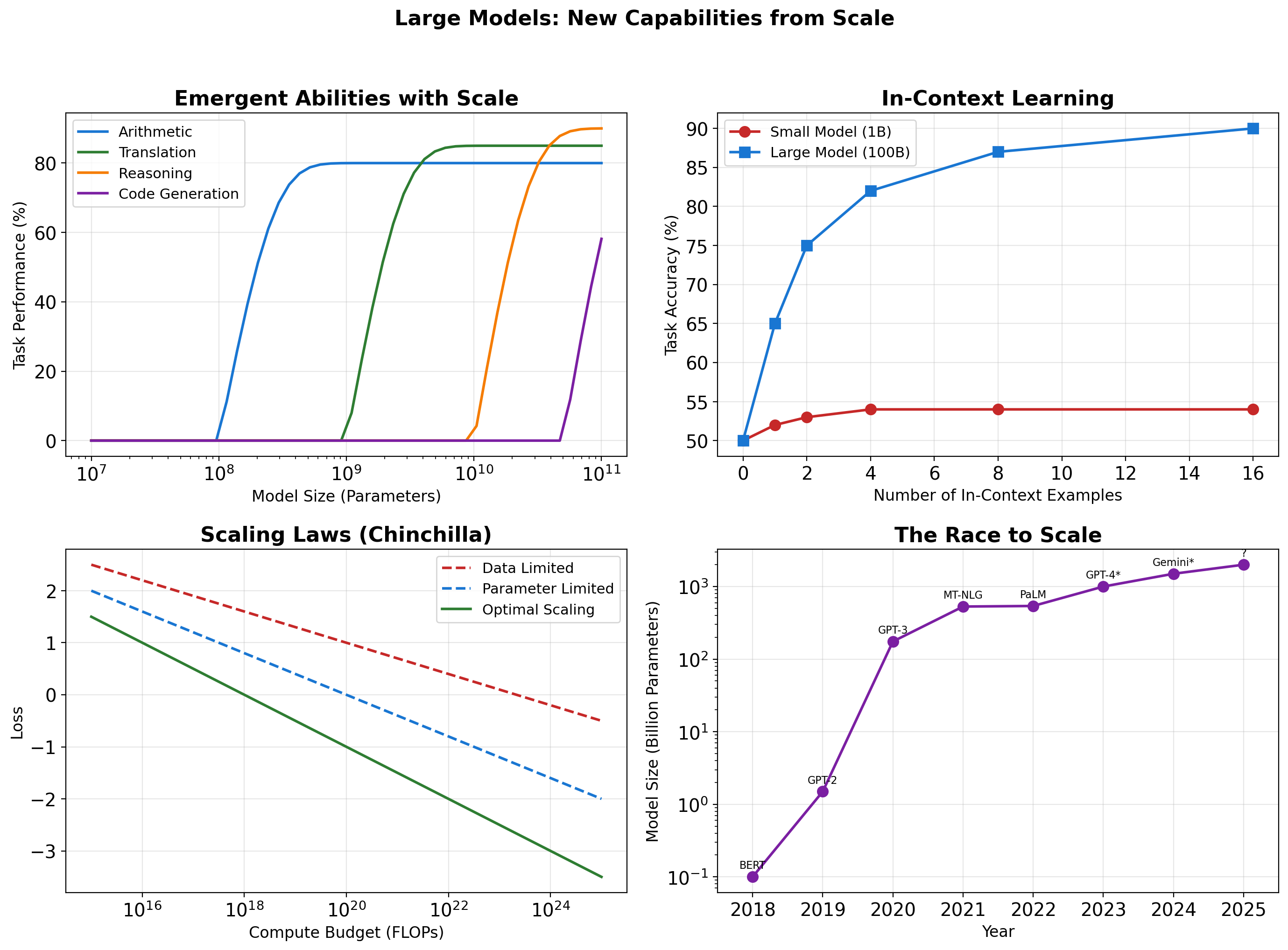
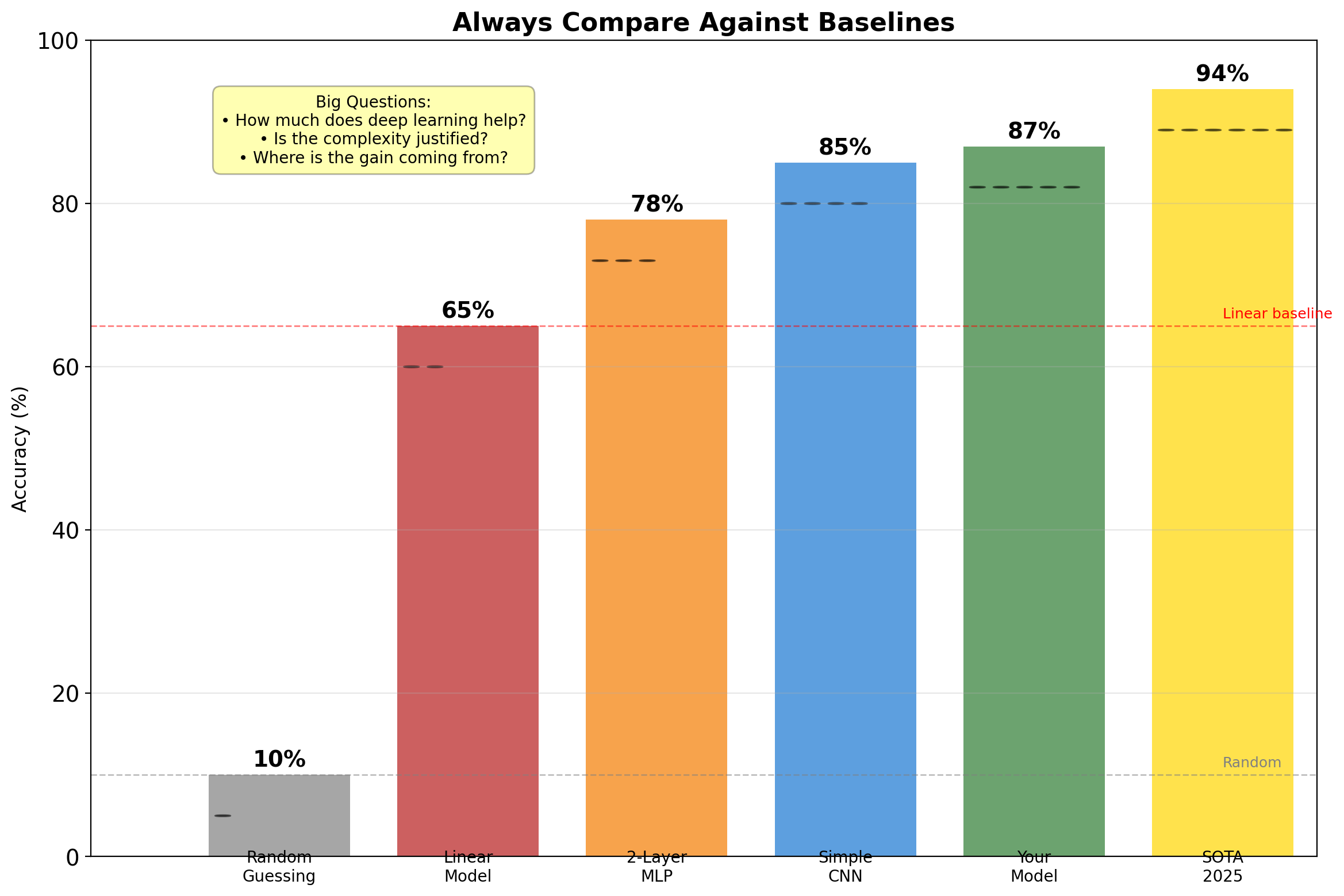
Always Establish Baselines Before Claiming Improvement
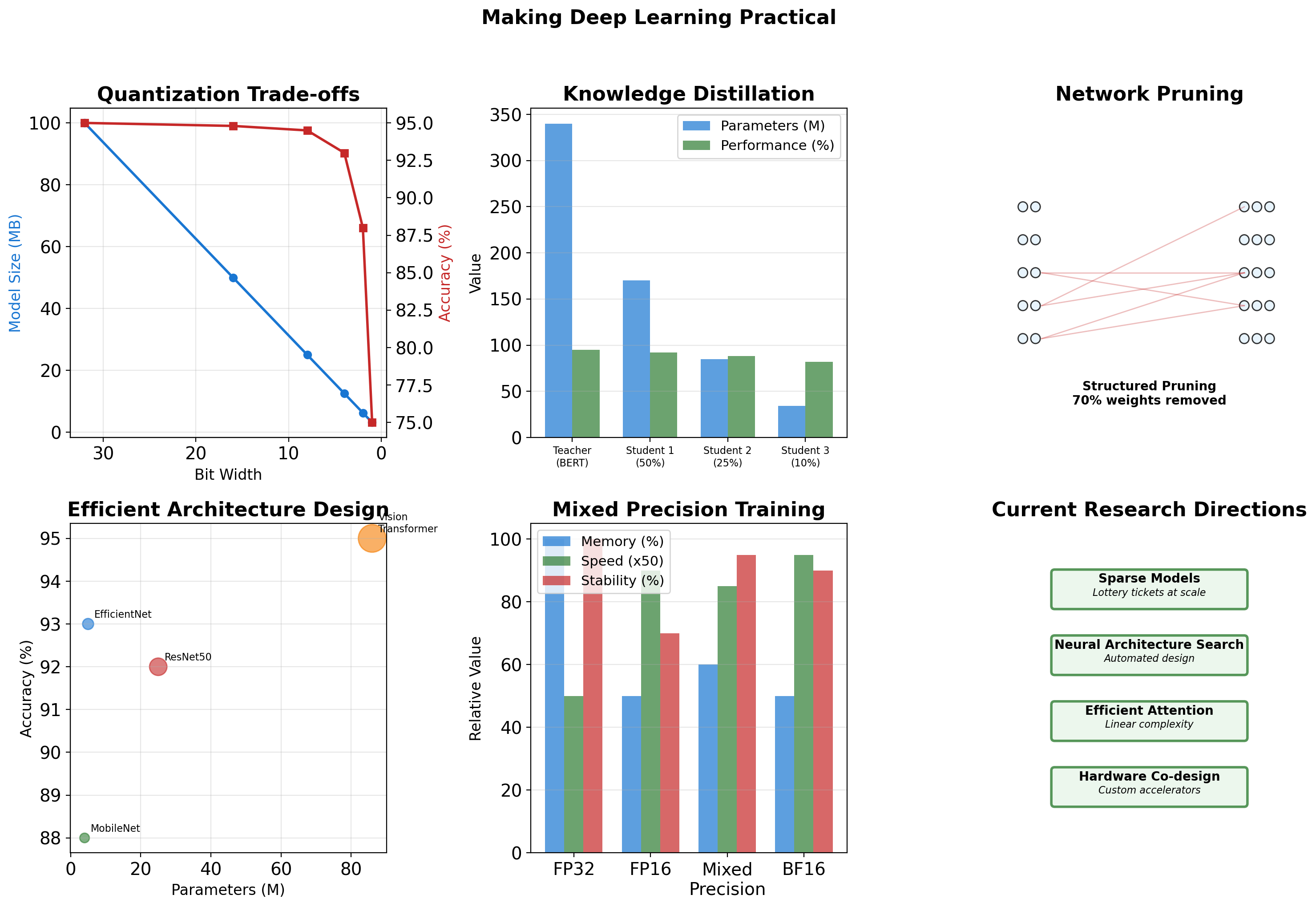
Current Frontiers & Course Roadmap
Course Architecture: Statistical to Neural
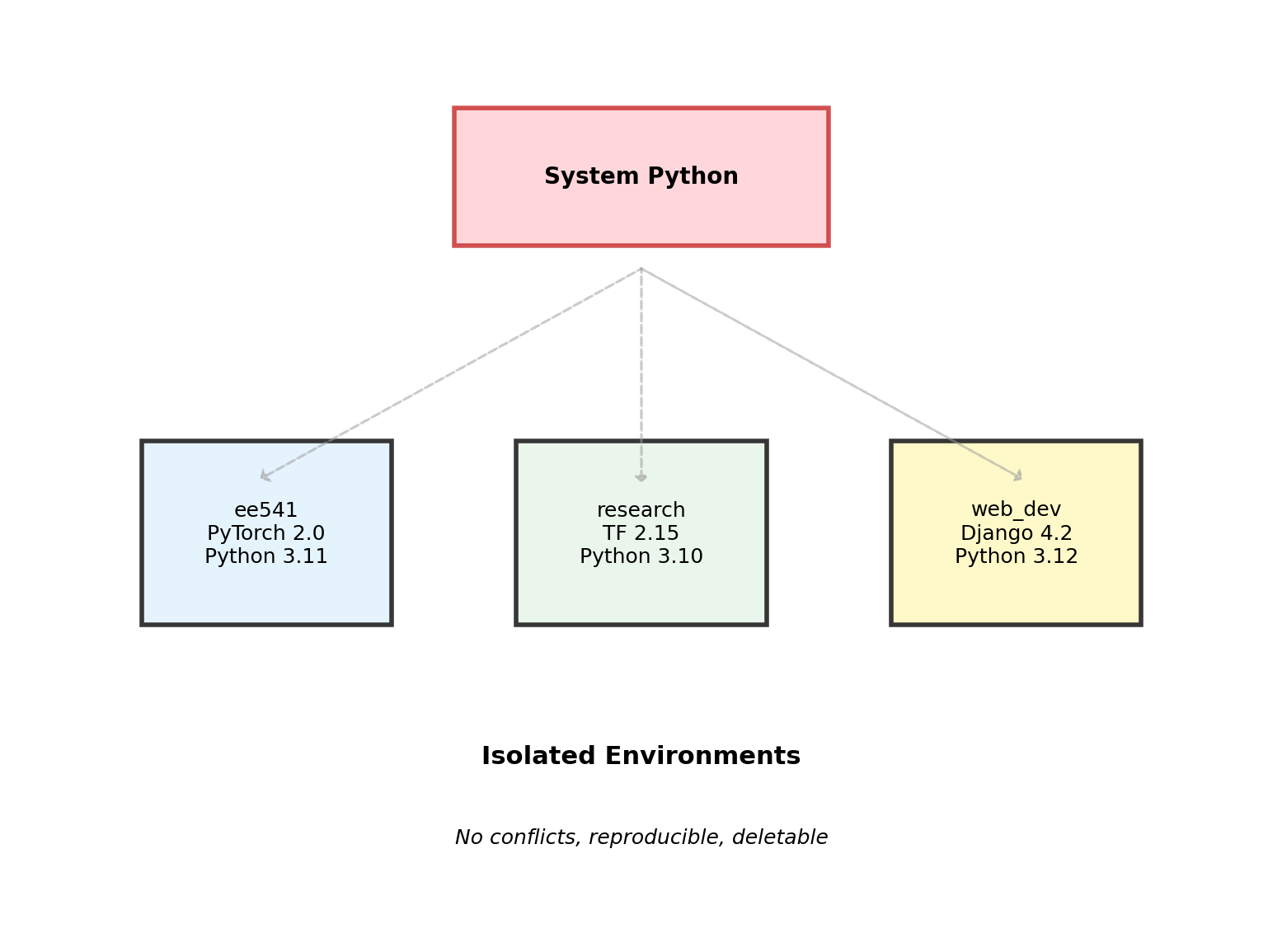
Scaling Laws and Emergent Capabilities
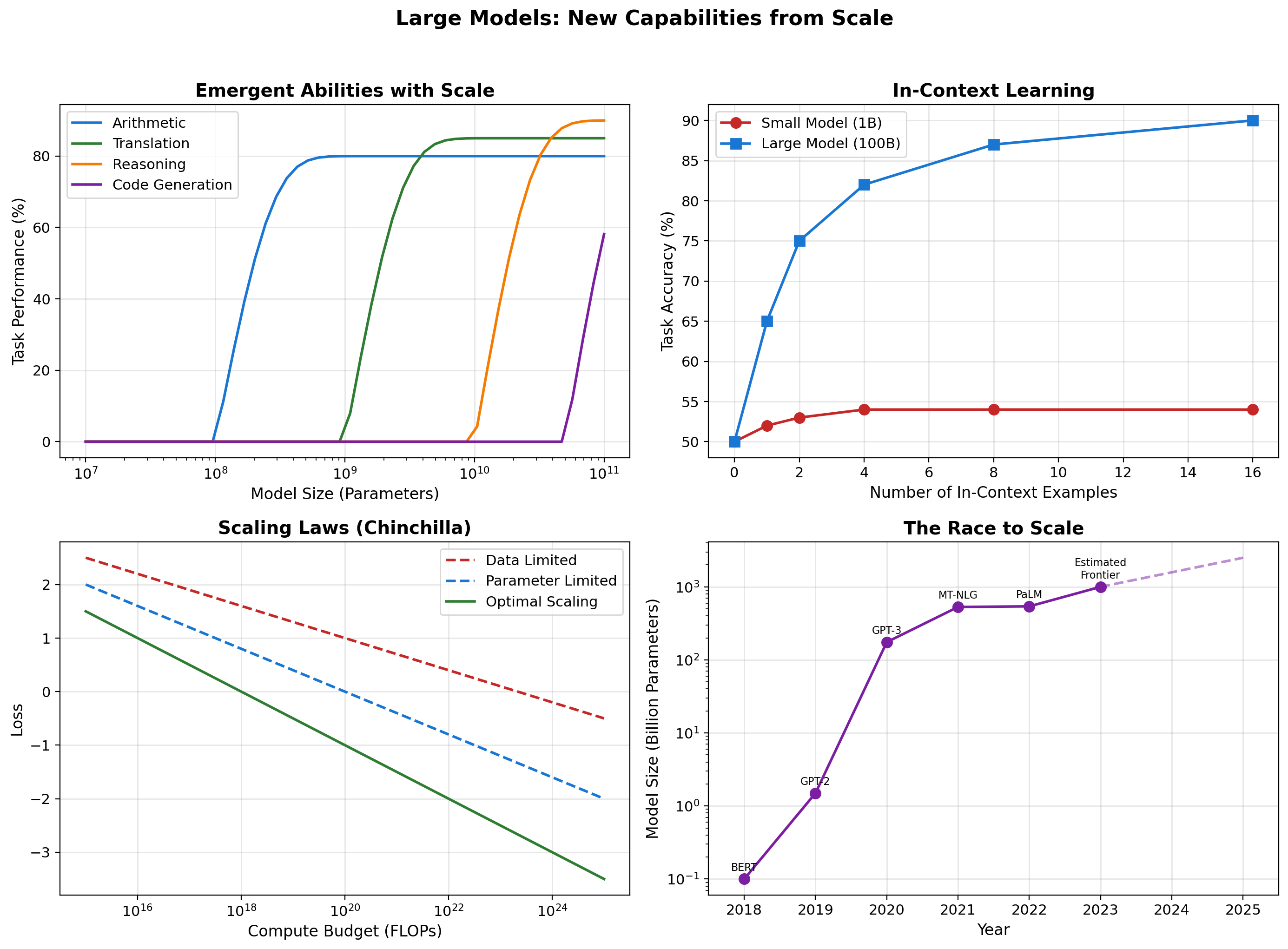
What these scales cost:
GPT-2 (1.5B params, 2019):
- Training: ~$50K compute, weeks on multi-GPU
- Inference: Runs on laptop CPU
GPT-3 (175B params, 2020):
- Training: ~$5M compute, months on cluster
- Inference: Requires GPU server
PaLM (540B params, 2022):
- Training: ~$10M+ compute, specialized infrastructure
- Inference: Multi-GPU required
Scale is not just about bigger numbers - it’s about fundamentally different resource requirements.
Model Compression and Acceleration
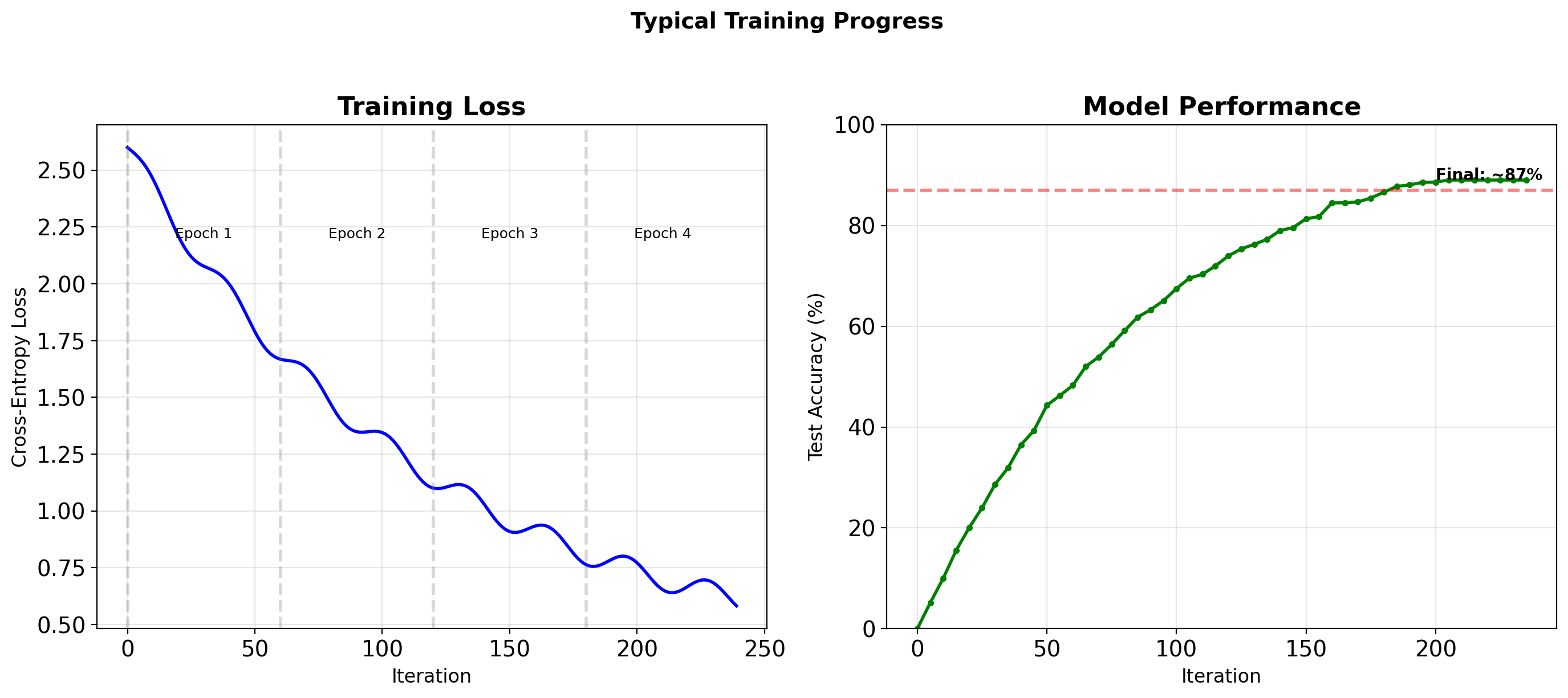
Python Environment Setup
Environment Management: Why It Matters
Dependency Conflicts
# System Python - Don't do this
python install torch
# Error: requires numpy>=1.19
pip install numpy==1.20
# Breaks: opencv requires numpy==1.18Conflicts are inevitable. Each project needs:
- Specific Python version
- Specific package versions
- Isolated from system Python
Virtual Environments
Conda: Package and Environment Management
Installation
# Download Miniconda (minimal) or Anaconda (full)
# miniconda.anaconda.com
# After installation, verify:
conda --version
conda info
# Update conda itself
conda update -n base condaCreate Course Environment
Why Conda for Deep Learning
Binary package management
- Precompiled CUDA libraries
- Optimized BLAS/LAPACK
- No compilation required
Cross-platform
- Same commands on Windows/Mac/Linux
- Handles system dependencies
Channel system
conda-forge: Community packagespytorch: Official PyTorch buildsnvidia: CUDA toolkit
Environment files
- Share exact environment
environment.ymlfor reproducibility
Essential Package Installation
# Activate your environment first
conda activate ee541
# Core scientific stack
conda install numpy scipy matplotlib pandas
# Jupyter for notebooks
conda install jupyter ipykernel
# Register kernel for Jupyter
python -m ipykernel install --user --name ee541 --display-name "Python (ee541)"
# PyTorch - SELECT BASED ON YOUR SYSTEM
# CPU only
conda install pytorch torchvision torchaudio cpuonly -c pytorch
# CUDA 11.8 (NVIDIA GPU)
conda install pytorch torchvision torchaudio pytorch-cuda=11.8 -c pytorch -c nvidia
# Mac M1/M2/M3 (Metal Performance Shaders)
conda install pytorch torchvision torchaudio -c pytorch
# Additional ML tools
conda install scikit-learn
conda install -c conda-forge tensorboardGPU Configuration Check
- NVIDIA: Check CUDA version with
nvidia-smi - AMD: ROCm support limited, use CPU fallback
- Mac (MPS): Automatic detection in PyTorch 1.12+
Jupyter Notebooks: Interactive Development
Starting Jupyter
# From terminal with environment active
(ee541) $ jupyter notebook
# Opens browser at localhost:8888
# Navigate to your work directoryNotebook Structure
- Cells: Code or Markdown
- Kernel: Python process executing code
- State: Variables persist between cells
Key Shortcuts
Shift+Enter: Run cell, move to nextCtrl+Enter: Run cell, stayEsc: Command modeEnter: Edit modeA/B: Insert cell above/below
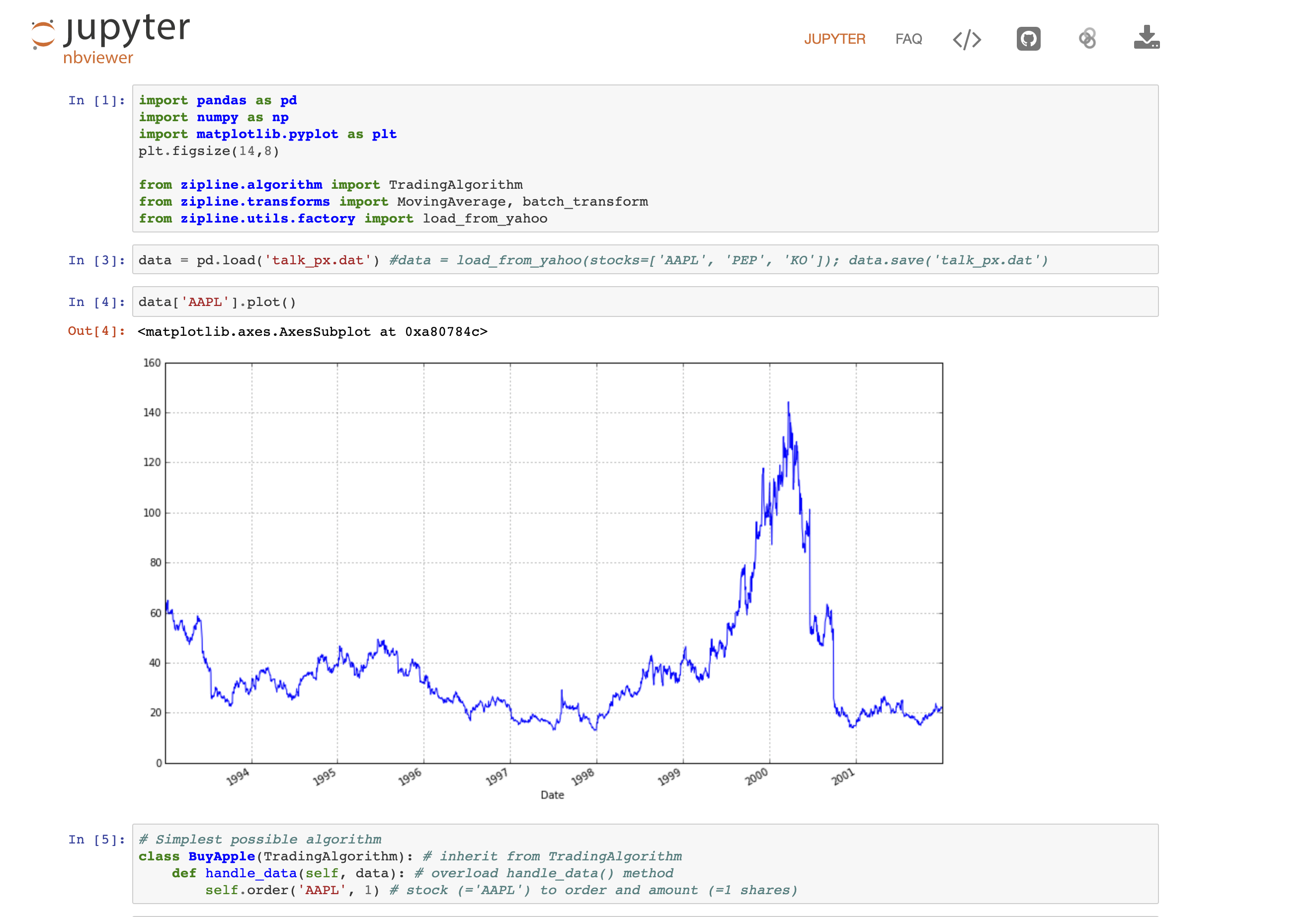
Real-World Example: Trading Algorithm
Project Management
Version Control
Verifying Your Environment
import sys
import platform
print(f"Python: {sys.version}")
print(f"Platform: {platform.platform()}")
packages = {
'numpy': None,
'torch': None,
'torchvision': None,
'matplotlib': None,
'jupyter': None,
'sklearn': 'scikit-learn'
}
for import_name, pip_name in packages.items():
try:
module = __import__(import_name)
version = getattr(module, '__version__', 'installed')
print(f"✓ {import_name}: {version}")
# Special check for PyTorch GPU
if import_name == 'torch':
import torch
if torch.cuda.is_available():
print(f" GPU: CUDA ({torch.version.cuda})")
print(f" Device: {torch.cuda.get_device_name(0)}")
elif torch.backends.mps.is_available():
print(f" GPU: MPS (Mac)")
else:
print(f" GPU: Not available")
except ImportError:
package = pip_name or import_name
print(f"✗ {import_name}: Not installed")
print(f" Install with: conda install {package}")Python: 3.11.8 | packaged by conda-forge | (main, Feb 16 2024, 20:49:36) [Clang 16.0.6 ]
Platform: macOS-26.2-arm64-arm-64bit
✓ numpy: 1.26.4
✓ torch: 2.5.1
GPU: MPS (Mac)
✓ torchvision: 0.20.1
✓ matplotlib: 3.10.6
✓ jupyter: installed
✓ sklearn: 1.6.1Environment Management Commands
Conda Essentials
Package Management
PyTorch Demo
Fashion-MNIST: 87% Accuracy in Four Epochs
What We’re Building
Task: Classify clothing items into 10 categories
Architecture: Simple 2-layer network
- Input: 28×28 grayscale images (784 pixels)
- Hidden: 128 neurons with ReLU
- Output: 10 classes (softmax)
Training: 4 epochs, Adam optimizer
Files:
1-fashion-mnist.ipynb: Dataset exploration2-minimal-pytorch.ipynb: Core training loop3-feature-visualization.ipynb: TensorBoard monitoring

T-shirt
Trouser

Pullover

Dress

Coat

Sandal

Shirt

Sneaker

Bag

Boot
Core Training Loop Structure
# Minimal.ipynb - Key components
# 1. Data Loading
train_loader = DataLoader(train_set, batch_size=100, shuffle=True)
test_loader = DataLoader(test_set, batch_size=100, shuffle=False)
# 2. Model Definition
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.hidden = nn.Linear(784, 128)
self.output = nn.Linear(128, 10)
def forward(self, x):
x = F.relu(self.hidden(x))
return self.output(x)
# 3. Training Loop
for epoch in range(num_epochs):
for images, labels in train_loader:
# Forward pass
outputs = model(images.view(-1, 784))
loss = loss_func(outputs, labels)
# Backward pass
optimizer.zero_grad()
loss.backward()
optimizer.step()Training Performance Benchmarks
Complete training in ~5 minutes on CPU, <1 minute on GPU
Training Dynamics
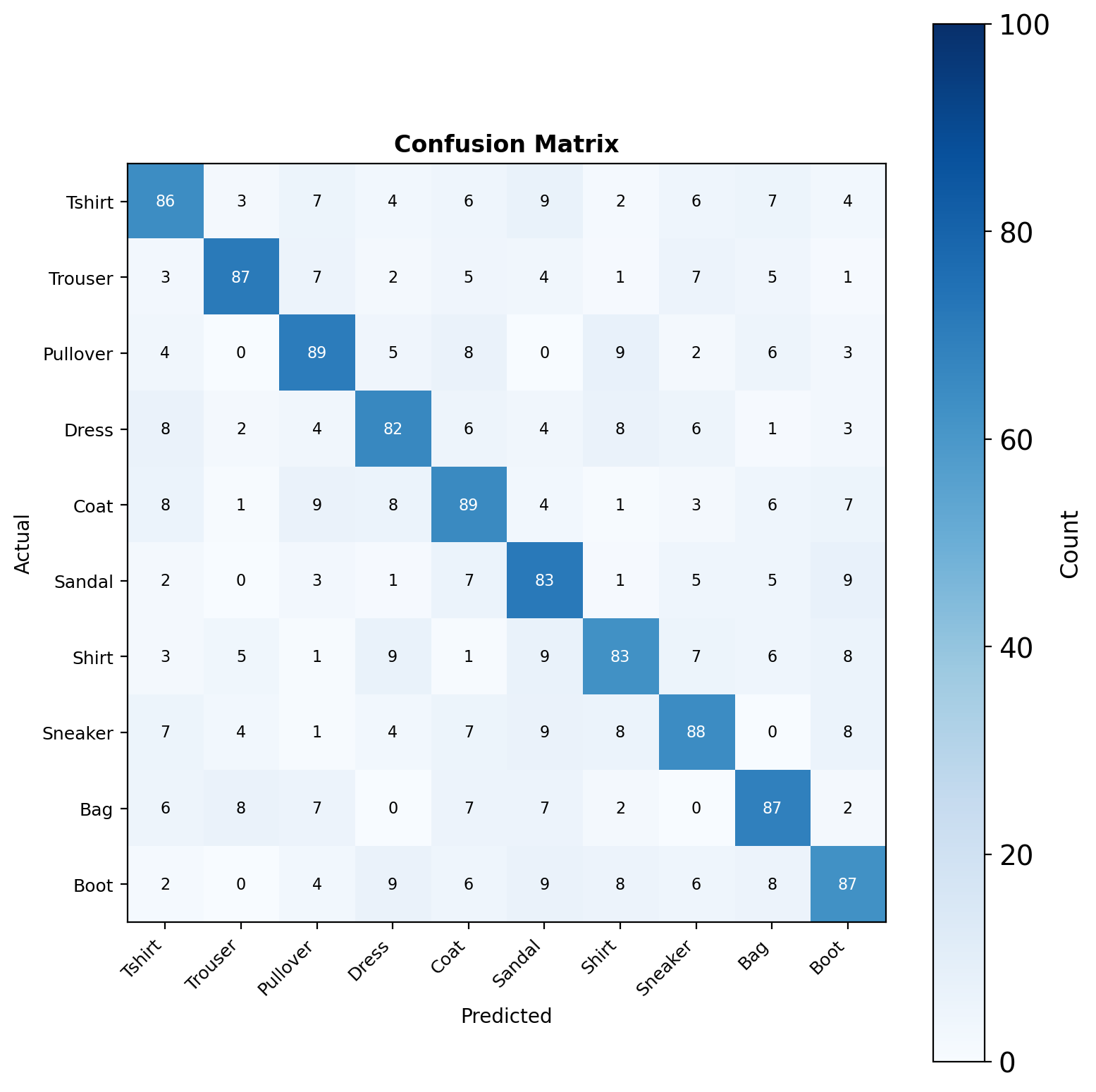
Observations:
- Rapid initial learning (first epoch)
- Diminishing returns with more training
- Test accuracy plateaus around 87% for this simple model
TensorBoard Visualization
Launch TensorBoard
Available Visualizations
- Scalars: Loss, accuracy over time
- Images: Sample predictions
- Graph: Network architecture
- Embeddings: Feature space (PCA/t-SNE)
- Histograms: Weight distributions
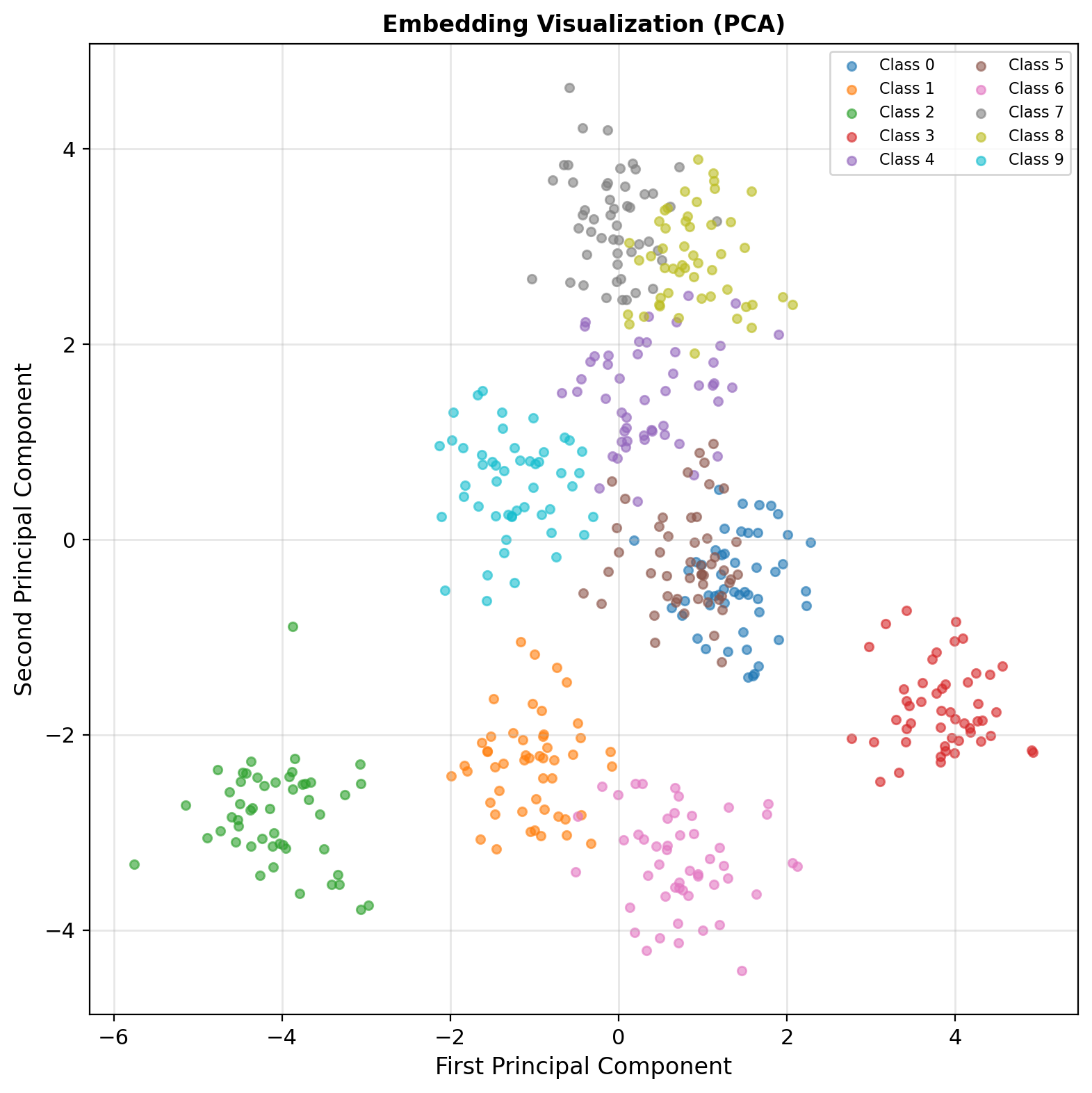
Embedding Insight: Classes form distinct clusters in feature space
Model Architecture Inspection
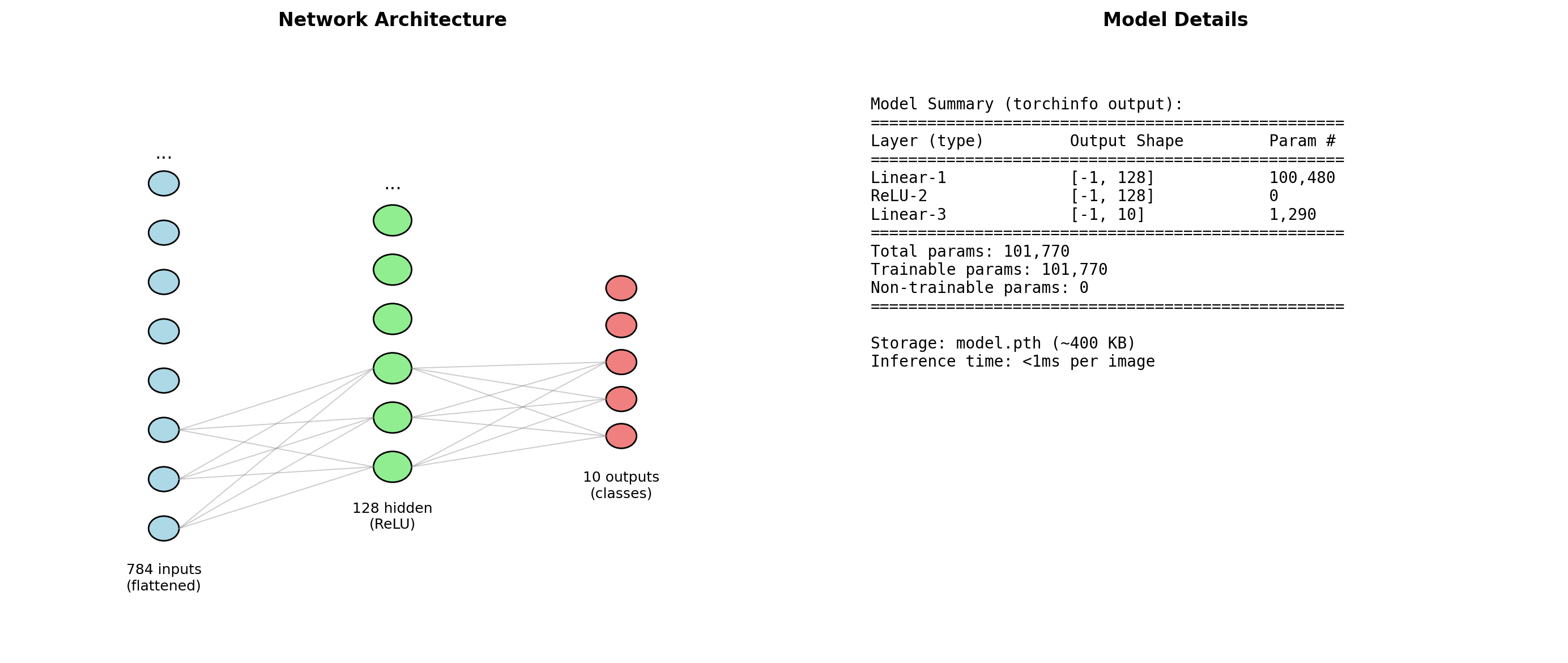
87% Accuracy Achieved with Simple Architecture
Implementation Results
- Model: 2-layer MLP with 128 hidden units
- Performance: 87% test accuracy after 4 epochs
- Training time: ~2 minutes on CPU
- Bottom line: Simple architectures work well for Fashion-MNIST
Not Addressed (Future Topics)
- Overfitting analysis: No train/val split comparison
- Hyperparameter tuning: Fixed learning rate, no grid search
- Architecture search: Only tried one configuration
- Regularization: No dropout, weight decay, or data augmentation
- Optimizer exploration: Only tried Adam, not SGD variants or AdamW
Main Files
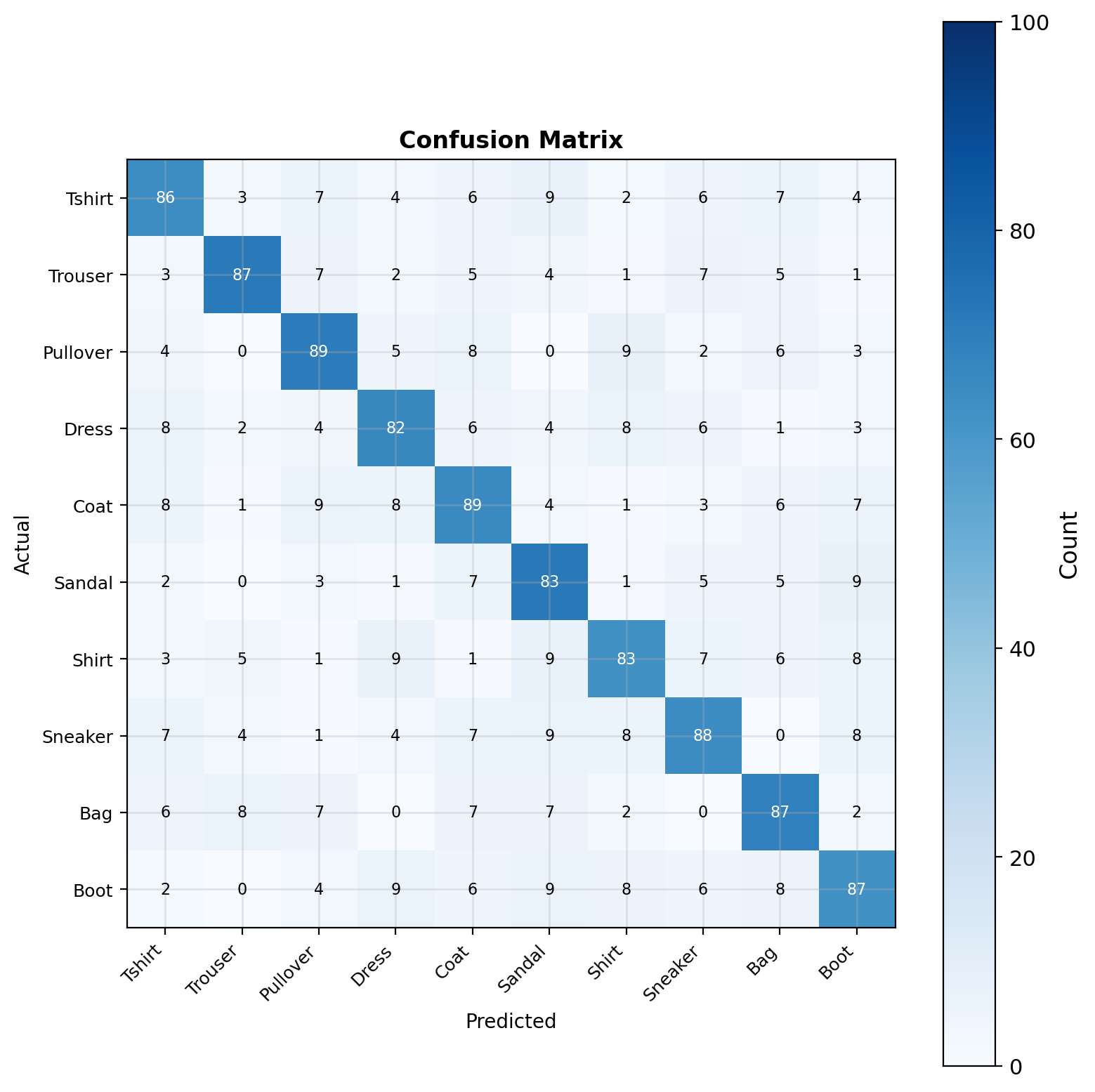
Common Confusions: Shirt ↔︎ T-shirt, Pullover ↔︎ Coat
Python and NumPy for Neural Networks
Next week: Array operations and automatic differentiation