Computational Deep Learning

EE 541 - Unit 1

Dr. Brandon Franzke

Spring 2026

Deep Learning

Opening sequence. Two slides that capture the course: (1) what a neural network computes, (2) what we’re really studying - how it learns.

How Neural Networks Learn

The training loop: Forward pass computes predictions, backward pass computes gradients, weights update. This cycle repeats thousands of times until the network learns.

Learning to Classify

This is what we study: How does a network learn to draw this boundary? What makes it work? When does it fail? This semester answers these questions.

What is Machine Learning?

Welcome to Deep Learning. This course bridges classical statistical signal processing with modern neural network methods. We’ll build from MMSE estimation through CNNs.

Learning = Task + Performance Measure + Experience

Herbert Simon (1983)

“Learning is any process by which a system improves performance from experience.”

Framework

\[\text{Learning System} = (\mathcal{T}, \mathcal{P}, \mathcal{E})\]

• Task \(\mathcal{T}\): What to accomplish
• Performance \(\mathcal{P}\): How to measure success
• Experience \(\mathcal{E}\): Data to learn from

Learning occurs when: \[\mathcal{P}_{\text{after}}(\mathcal{T}, \mathcal{E}) > \mathcal{P}_{\text{before}}(\mathcal{T})\]

Example: Email Spam Filter

• Task (\(\mathcal{T}\)): Classify emails as spam/not spam
• Performance (\(\mathcal{P}\)): % correctly classified
• Experience (\(\mathcal{E}\)): Database of labeled emails

Example: Self-Driving Car

• \(\mathcal{T}\): Navigate roads safely
• \(\mathcal{P}\): Miles without intervention
• \(\mathcal{E}\): Hours of human driving data

This framework lets us analyze any learning problem systematically. Notice how different tasks share the same structure.

Generalization is the Goal of Machine Learning

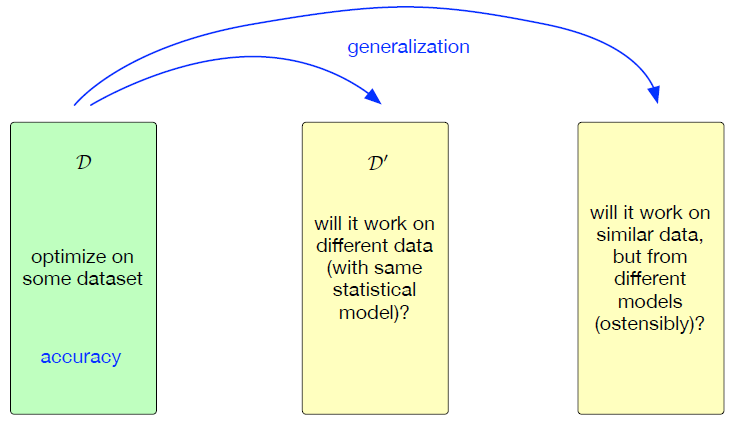
• Do not care about performance on the dataset we have
• Do care about performance on similar data that has no labels
• Accuracy/Generalization trade-off (bias-variance trade):
  • Optimizing accuracy to the extreme reduces capability to generalize

The fundamental challenge: we optimize on dataset \(\mathcal{D}\) (with labels) but need performance on \(\mathcal{D}'\) (without labels). This tension between fitting the training data and generalizing to new data defines the entire field.

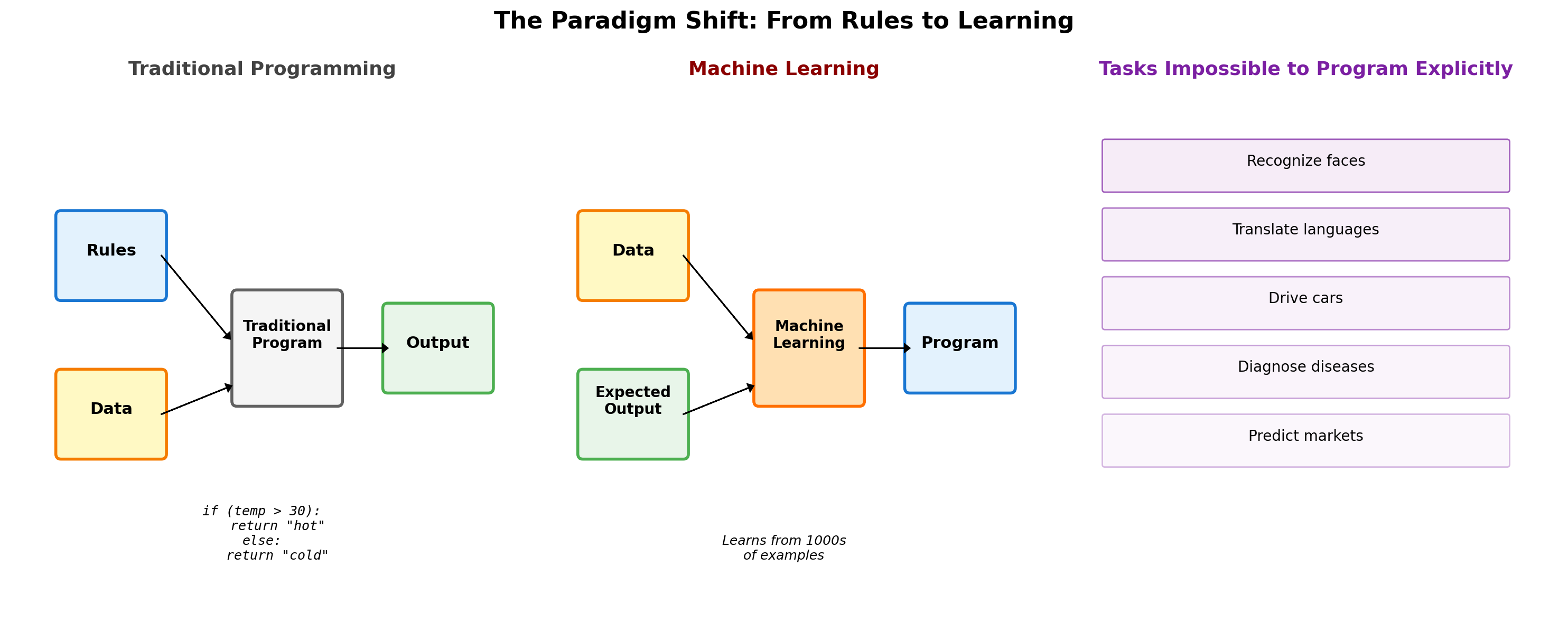
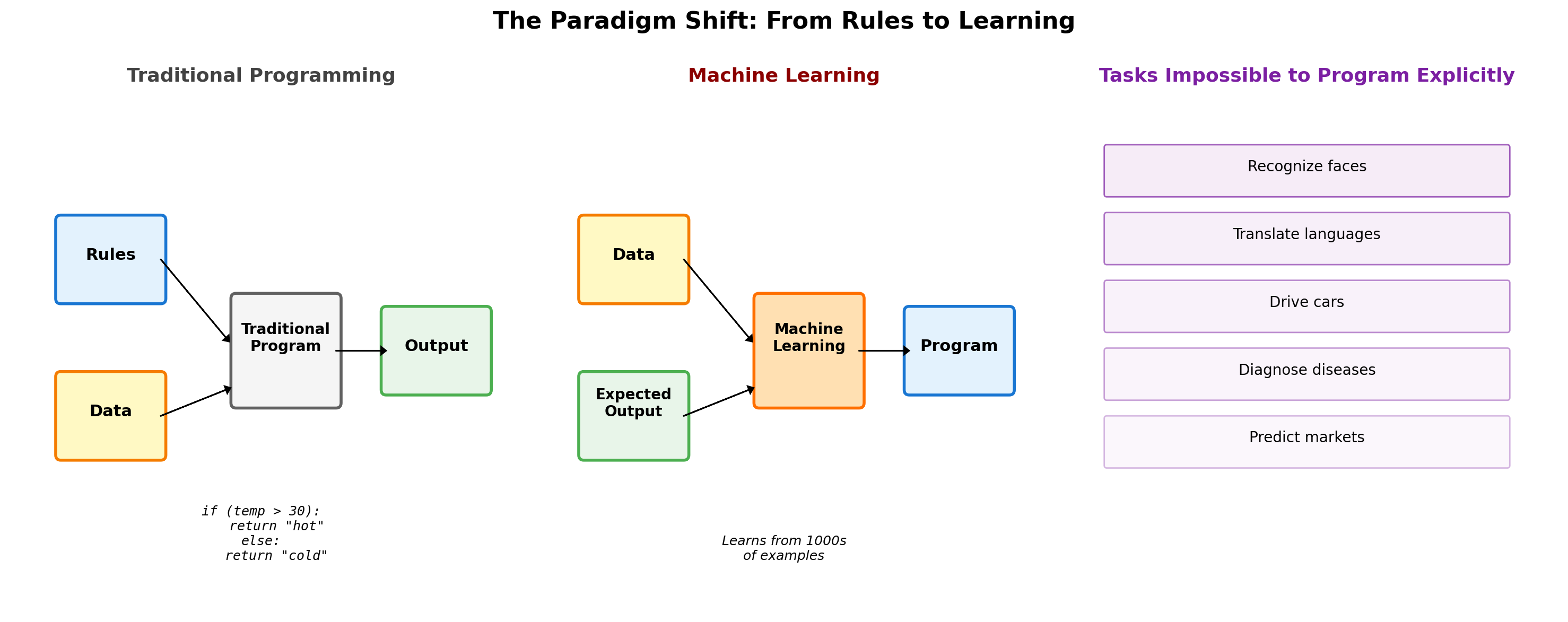
Machine Learning Inverts Traditional Programming

This shows the fundamental paradigm shift. Traditional programming requires us to specify rules, ML learns them from examples.

Theory-Driven vs Data-Driven Approaches

Classical: Theory-Driven

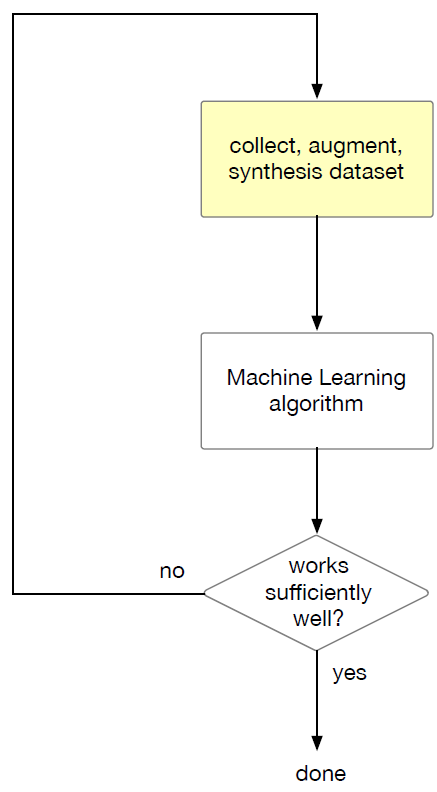
Modern: Data-Driven

From deriving models from first principles to learning them from data. Both approaches remain valid for different problems.

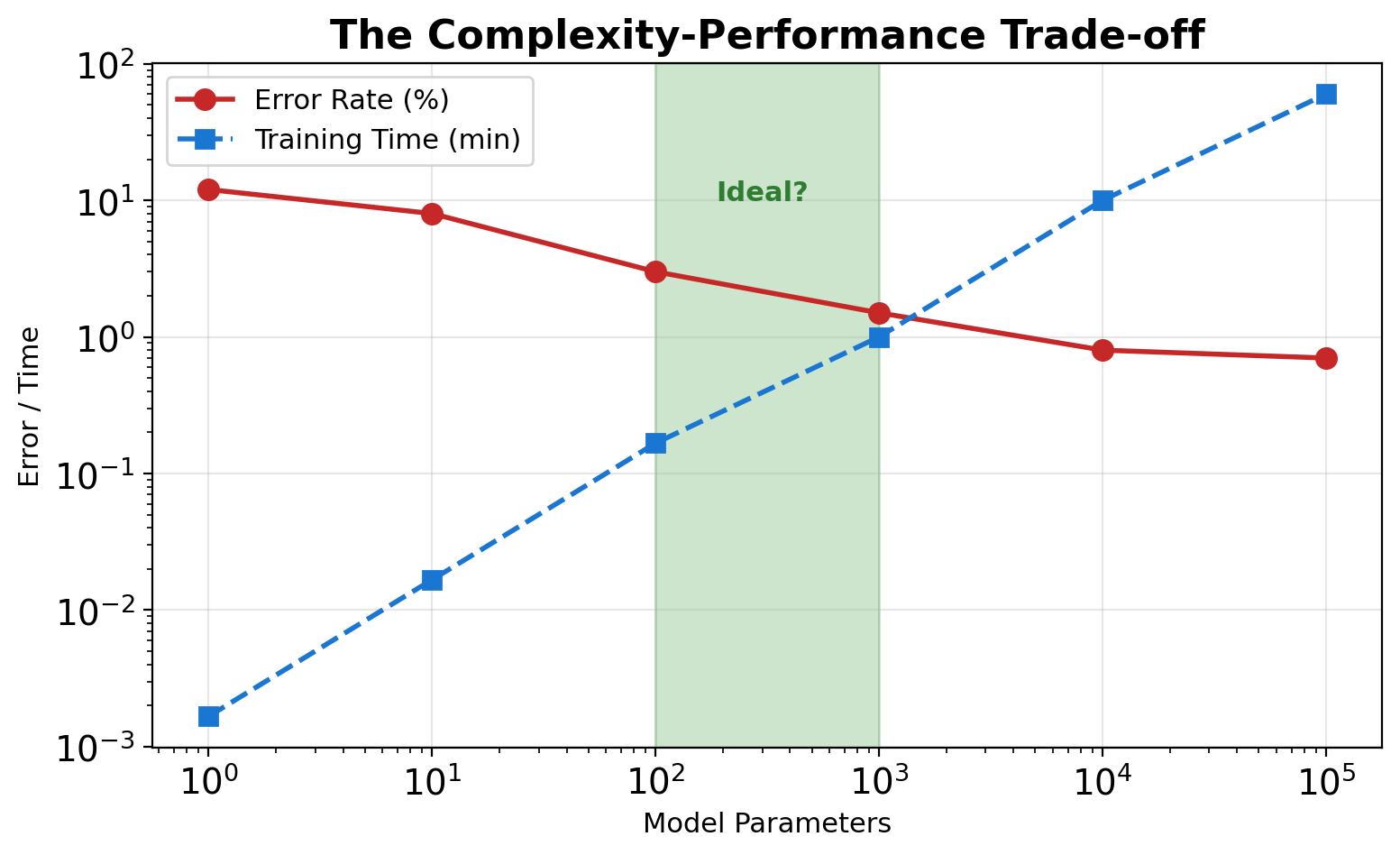
Model Complexity: When to Stop Adding Parameters

George Box (1976)

“All models are wrong, but some are useful”

“Since all models are wrong the scientist cannot obtain a ‘correct’ one by excessive elaboration”

Box’s warning: More parameters ≠ better science

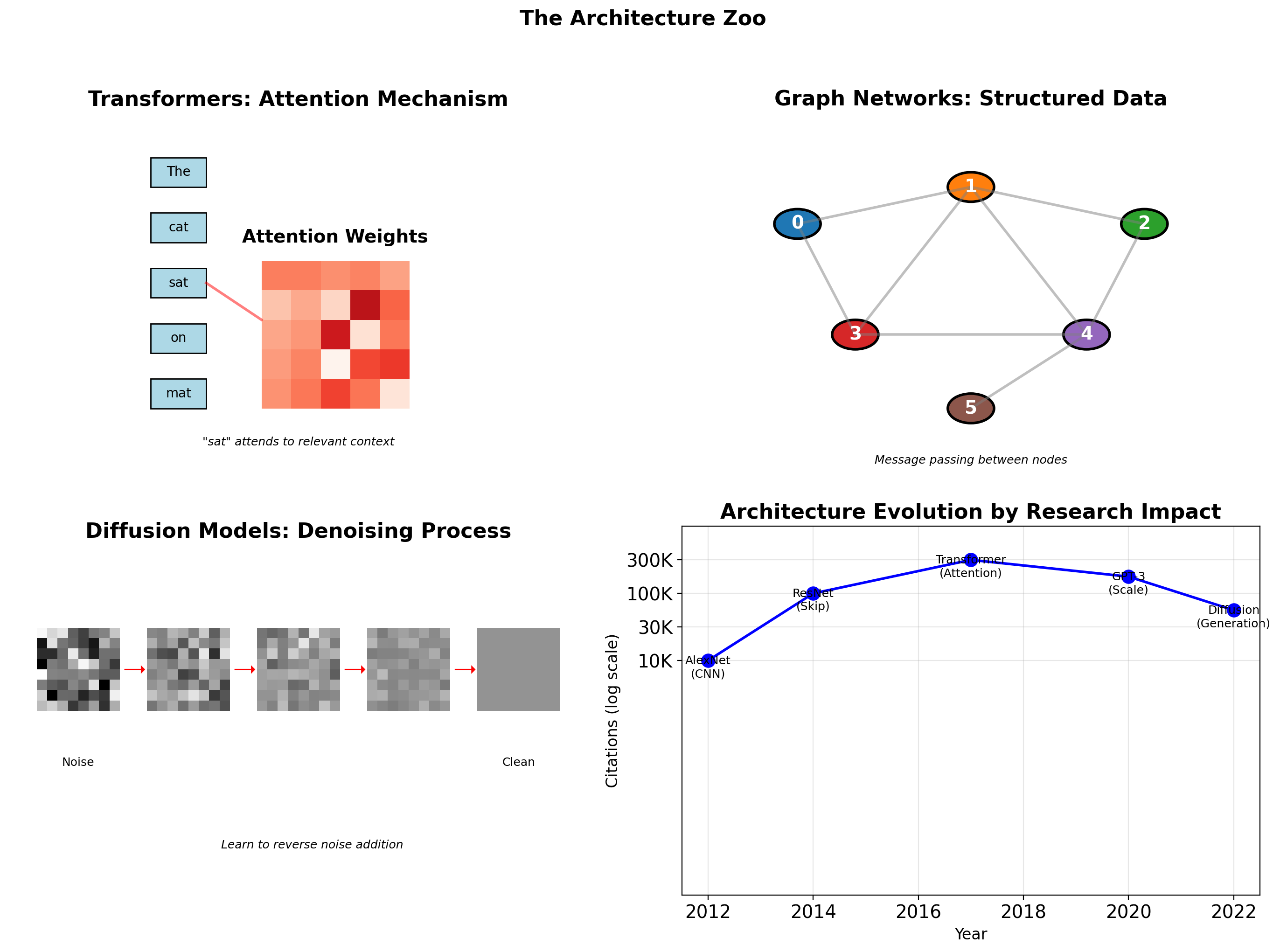
MNIST Classification: Accuracy vs Complexity

• Nearest neighbor: 3% error, \(\mathcal{O}(n)\) inference
• Linear classifier: 8% error, \(\mathcal{O}(d)\) inference
• 2-layer network: 2% error, 50K parameters
• ConvNet (LeNet-5): 0.8% error, 60K parameters
• ResNet-50: 0.2% error, 25M parameters

Question: Is 0.2% → 0.1% worth 25M parameters?

Worrying Selectively

It is inappropriate to be concerned about mice when there are tigers abroad

• Start simple
• Add complexity purposefully
• Validate empirically

This philosophy guides the course approach - preferring simple models that generalize over complex ones that overfit.

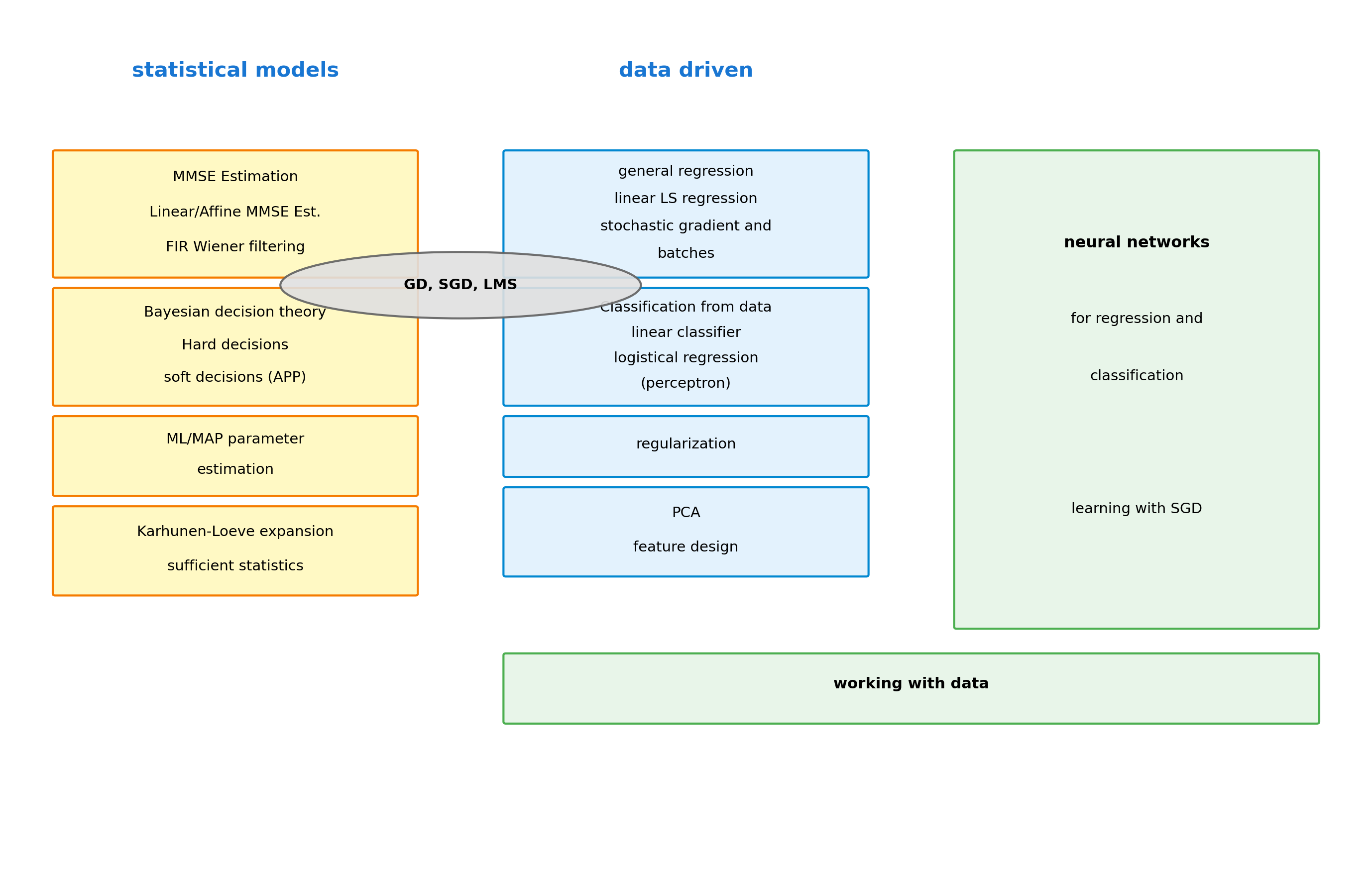
Course Structure: Statistical Foundations to Neural Networks

This slide shows the course’s intellectual structure: bridging classical statistical methods (left) with modern data-driven approaches (right), connected through optimization techniques (center). Green represents the neural network methods that unify both perspectives.

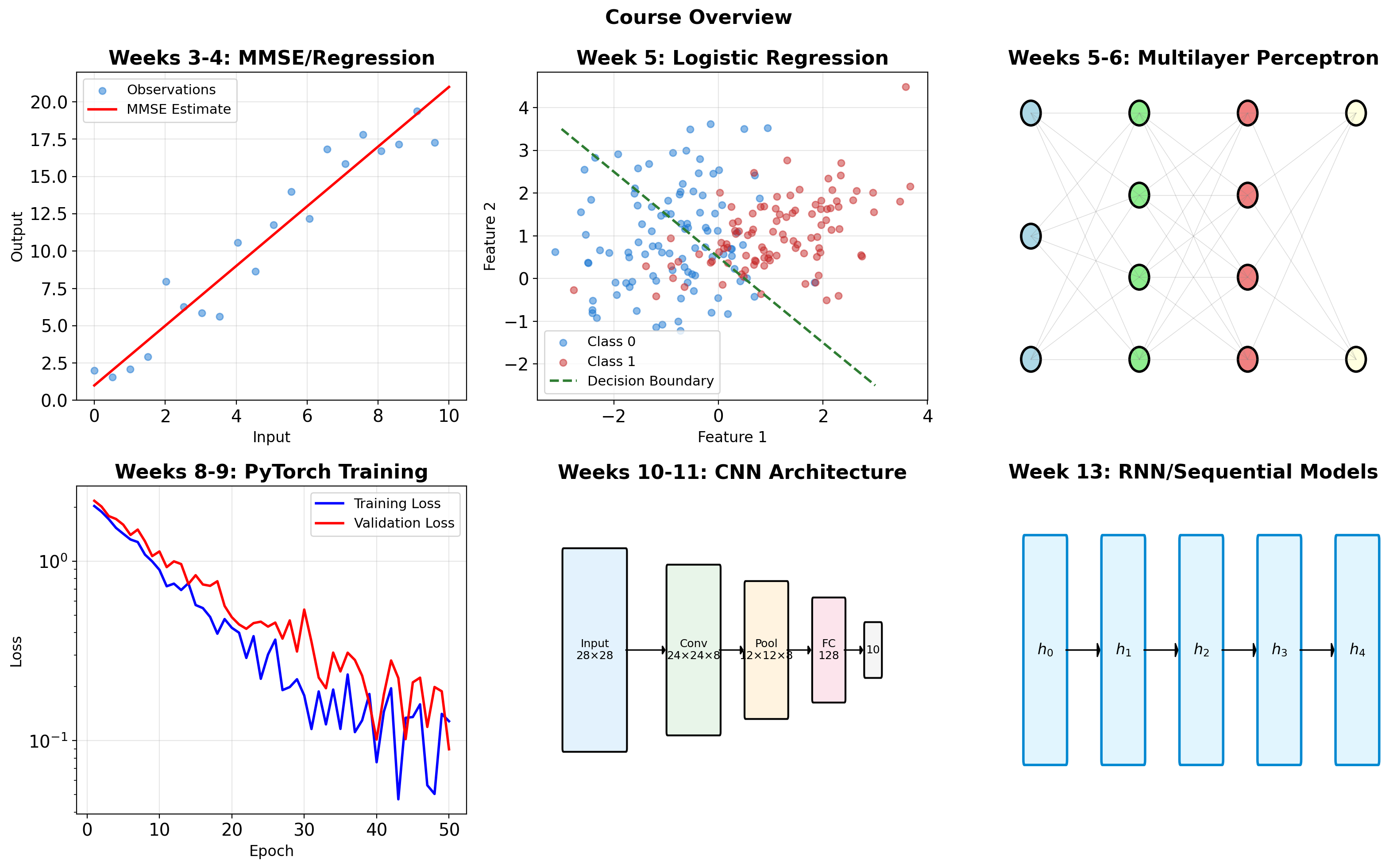
Semester Progression: MMSE to Convolutional Networks

This visualization shows the progression through the semester. Notice how we build from statistical foundations to neural architectures.

Outline

Foundations

Learning Framework

• Task, performance, experience
• Generalization as the goal

Hypothesis Classes

• Linear models and their limits
• Bias-variance tradeoff

Data

• Quality vs quantity
• Representation and dimensionality

Learning Paradigms

• Supervised, unsupervised, reinforcement
• Self-supervised methods

Neural Networks

Architecture

• Perceptron to deep networks
• Universal approximation
• Width vs depth

Optimization

• Loss landscapes
• SGD and variants

Generalization

• The mystery of why networks work

Practice

Environment Setup

PyTorch Demo

• Fashion-MNIST classifier

We’ll move from theory to practice today, ending with actually training a network together.

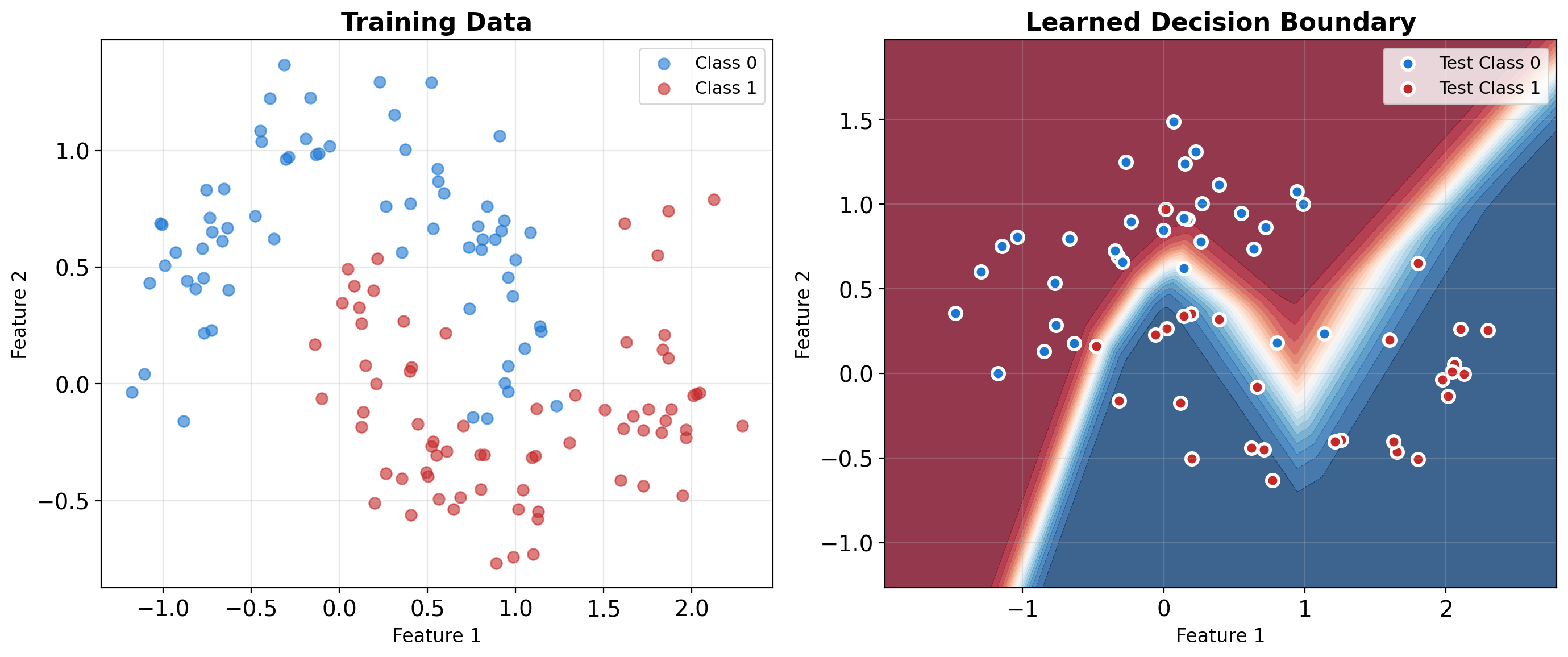
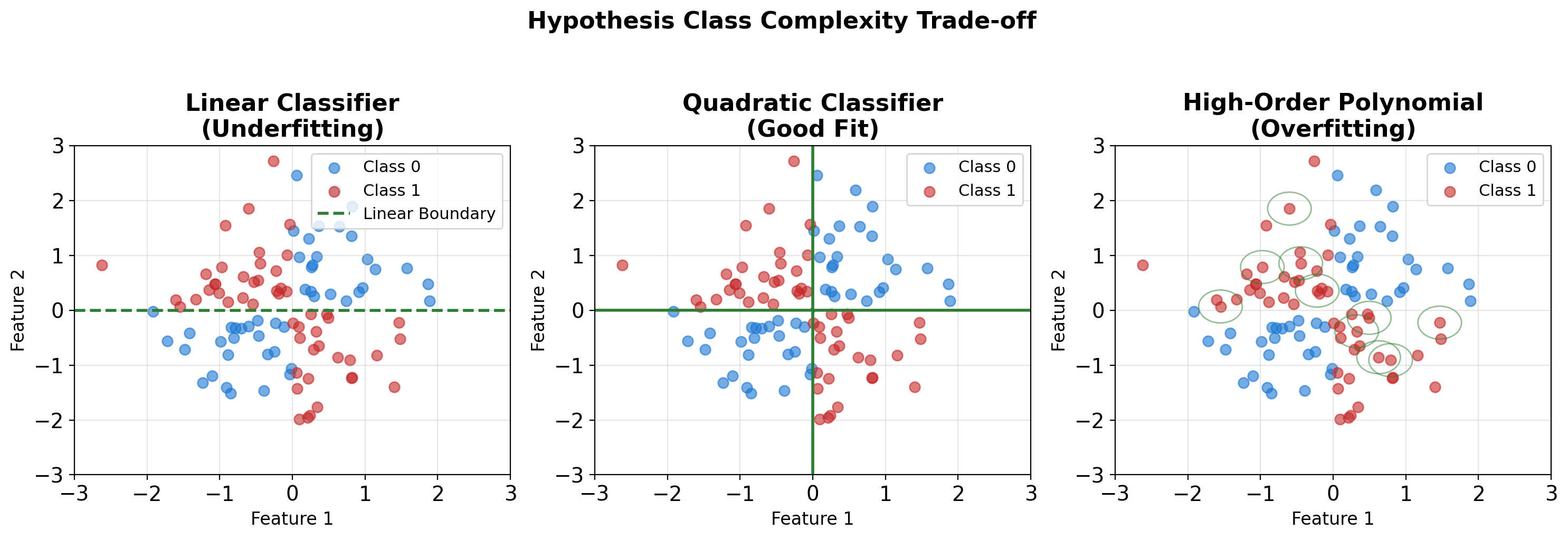
Linear Models Fail on Nonlinear Boundaries

Two-Moons Dataset

Tests whether a model can learn curved decision boundaries. Two interleaving half-circles that cannot be separated by any straight line.

This shows the fundamental limitation of linear models. The data has a nonlinear structure that cannot be captured by a straight line.

Neural Networks Learn Nonlinear Decision Boundaries

import numpy as np
from sklearn.neural_network import MLPClassifier
from sklearn.datasets import make_moons
from sklearn.model_selection import train_test_split

X, y = make_moons(n_samples=200, noise=0.2, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.3, random_state=42
)

mlp = MLPClassifier(
    hidden_layer_sizes=(10, 10), 
    max_iter=1000, 
    random_state=42
)
mlp.fit(X_train, y_train)

print(f"Training accuracy: {mlp.score(X_train, y_train):.3f}")
print(f"Test accuracy: {mlp.score(X_test, y_test):.3f}")

Training accuracy: 0.979
Test accuracy: 0.950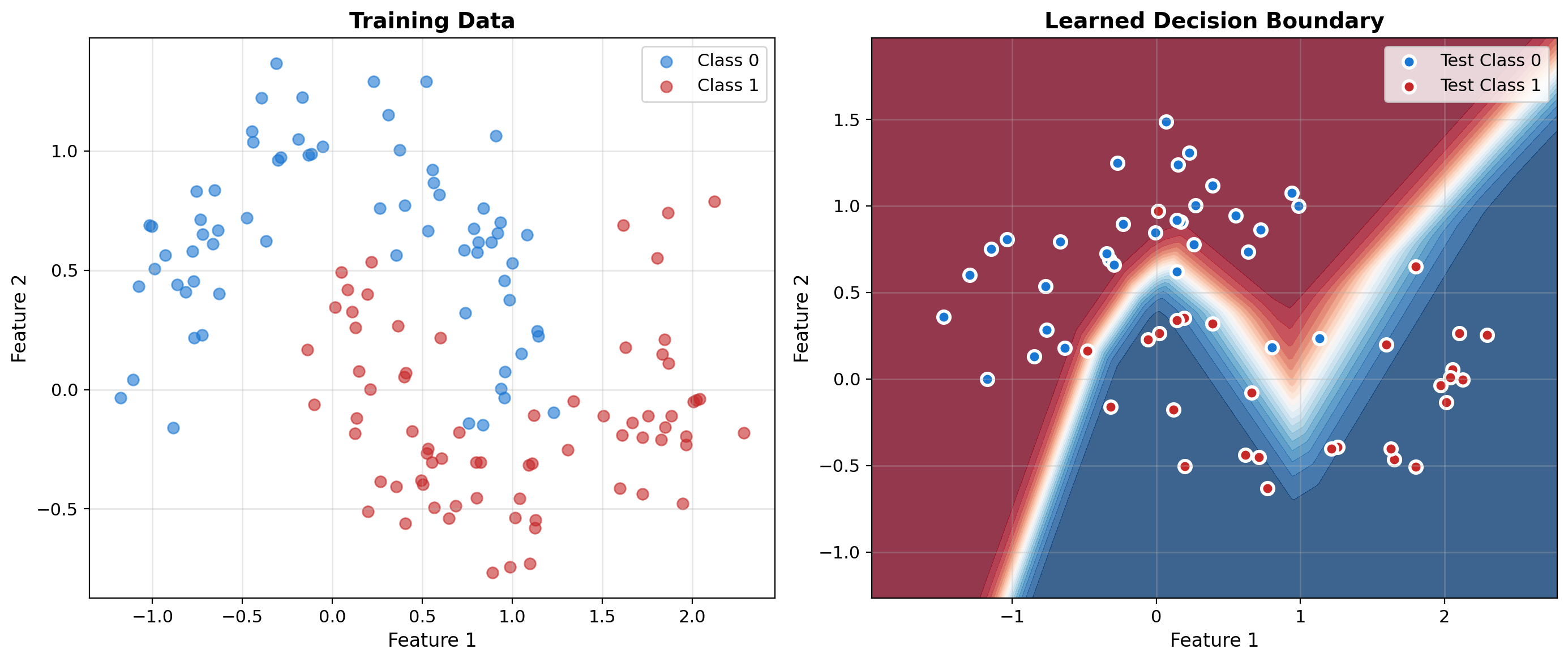

This simple example shows a neural network learning a non-linear decision boundary - something linear models cannot do. But neural networks need sufficient data to learn these boundaries - with only 10-20 samples, linear models often win.

Learning Fundamentals

Minimize Expected Risk Using Only Finite Samples

Given

• Training data: \(\mathcal{D} = \{(\mathbf{x}_i, y_i)\}_{i=1}^N\)
• Hypothesis class: \(\mathcal{H}\)
• Loss function: \(\mathcal{L}\)

Goal

Find \(h^* \in \mathcal{H}\) that minimizes:

\[\mathbb{E}_{(\mathbf{x},y) \sim P}[\mathcal{L}(h(\mathbf{x}), y)]\]

But we only have access to:

\[\frac{1}{N}\sum_{i=1}^N \mathcal{L}(h(\mathbf{x}_i), y_i)\]

Generalization Gap

Minimize error on unseen data using only observed samples

This gap defines machine learning

The gap between expected risk and empirical risk is fundamental to all of machine learning.

Example Task: “2s” Detector

A concrete example of a learning task: detecting the digit “2” from handwritten inputs. This illustrates the input-output mapping we want to learn.

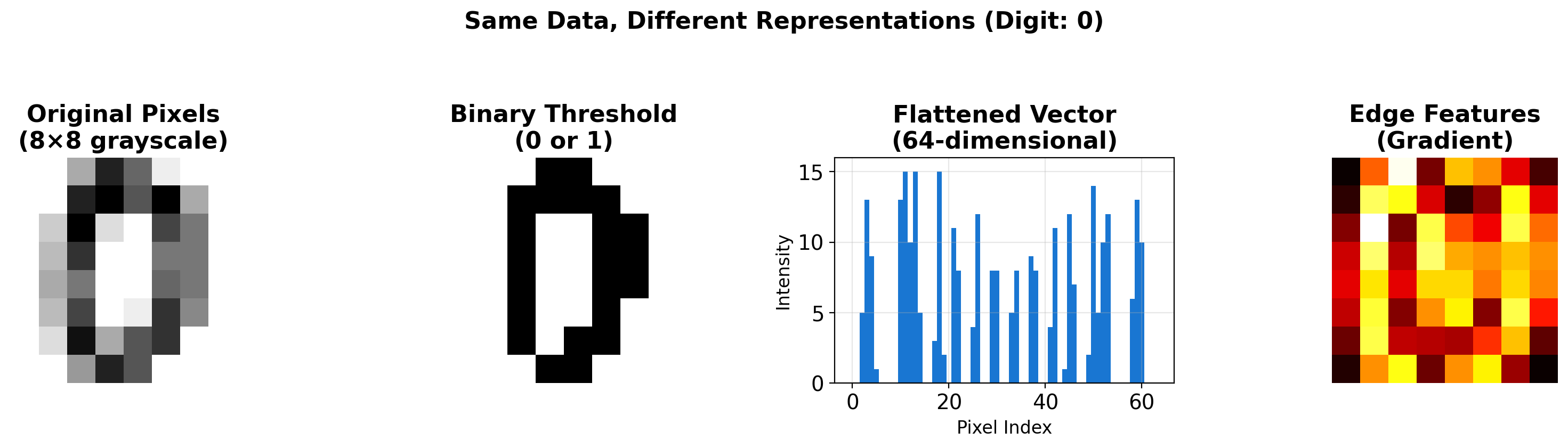
MNIST: Input and Output Representations

Input Space

• Raw pixels: \(\mathbf{x} \in \{0,255\}^{784}\)
• Normalized: \(\mathbf{x} \in [0,1]^{784}\)
• Binary: \(\mathbf{x} \in \{0,1\}^{784}\)

Output Space

• Classification: \(y \in \{0,1,...,9\}\)
• One-hot: \(\mathbf{y} \in \{0,1\}^{10}\)
• Probability: \(\mathbf{y} \in [0,1]^{10}\)

MNIST is our “Hello World” - simple enough to understand, complex enough to be non-trivial. Notice how representation choices matter.

Same Data, Multiple Representations

Representation Determines Learnability

The choice of representation can make learning tractable or impossible. Deep learning learns representations automatically.

Different representations expose different structure in the data. Deep learning’s power comes from learning good representations automatically.

Example: The Data Domain

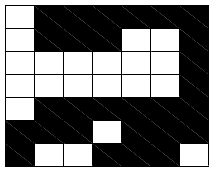
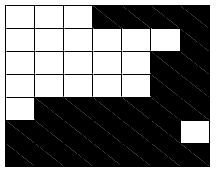
GOOD

GOOD

BAD

?

The choice of how to represent input is very important

Can we classify the unknown pattern?

Progressive reveal: First show one GOOD pattern, then second GOOD pattern (both stay visible), then BAD pattern appears, finally the question mark with unknown pattern. This shows the classification challenge.

Converting Pattern to Binary Vector

Binary Representation

x = 0111111011100100000010000
    001011111111101111001110

Label: “GOOD”

Key Insight

The same pattern can be represented as:

• Raw pixels
• Binary vectors (length d = 49)
• Feature vectors
• Learned representations

A hypothesis class can succeed or fail based on the choice of representation.

Converting the pattern to a binary bit string representation allows us to use linear classifiers. This is our first hint at the power of representation.

Linear Classifier on Binary Representation

Representation: Binary vectors, length \(d = 49\)

\[\mathbf{x} = \begin{bmatrix} 0111111011100100000010000 \\ 001011111111101111001110 \end{bmatrix}\]

\[y \in \{-1, +1\}\]

Hypothesize mapping data to label using linear classifier:

\[\hat{y} = \text{sign}(\mathbf{w} \cdot \mathbf{x}) = \text{sign}(w_1 x_1 + \cdots + w_{49} x_{49})\]

Definition: Linear Function

A function \(f: \mathbb{R}^d \rightarrow \mathbb{R}\) is linear if \(f(\mathbf{x}) = \mathbf{w}^\top \mathbf{x} + b\) for some \(\mathbf{w} \in \mathbb{R}^d\) and \(b \in \mathbb{R}\). The decision boundary \(\{\mathbf{x} : f(\mathbf{x}) = 0\}\) is a hyperplane.

where:

• \(\mathbf{w}\): Parameters to learn (weight vector)
• \(\hat{y}\): Predicted label (sign of linear combination)

This is the first introduction of LINEAR classification in the course. The linear hypothesis class will be our starting point, leading naturally to the next slide about linear vs nonlinear hypothesis classes.

Linear vs Nonlinear Hypothesis Classes

\[\mathcal{H}_{\text{linear}}: h(\mathbf{x}) = \text{sign}(\mathbf{w}^T\mathbf{x} + b)\] \[\mathcal{H}_{\text{neural}}: h(\mathbf{x}) = h_2(\mathbf{W}_2 \cdot h_1(\mathbf{W}_1\mathbf{x} + \mathbf{b}_1) + \mathbf{b}_2)\]

The hypothesis class determines what functions we can learn. Too simple: underfitting. Too complex: overfitting. Neural networks give us a flexible middle ground.

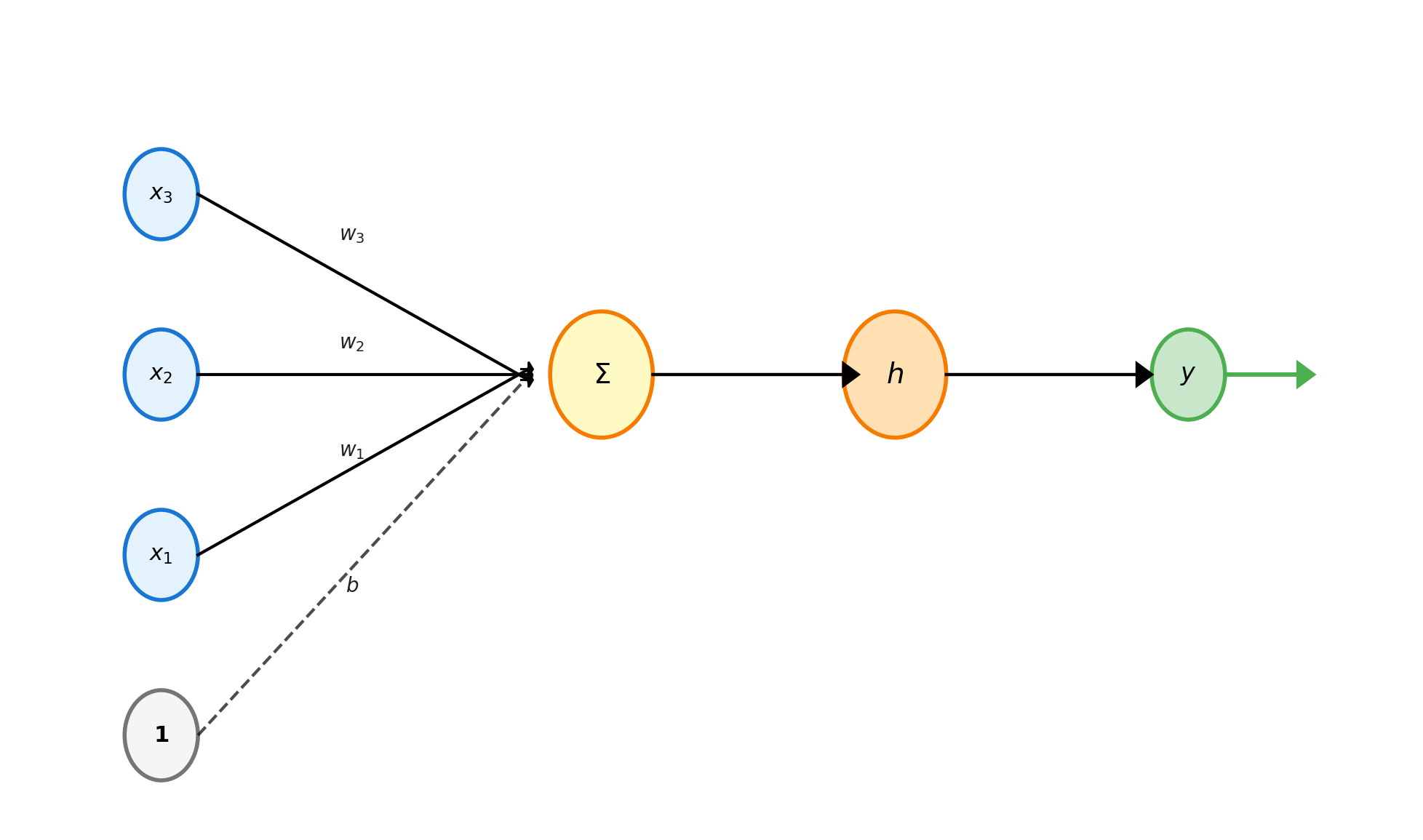
Perceptron: Linear Combination + Nonlinearity

Mathematical Model

\[y = h\left(\sum_{i=1}^n w_i x_i + b\right) = h(\mathbf{w}^T\mathbf{x} + b)\]

where \(h\) is an activation function:

• Step: \(h(z) = \begin{cases} 1 & z \geq 0 \\ 0 & z < 0 \end{cases}\)
• Sigmoid: \(h(z) = \frac{1}{1 + e^{-z}}\)
• ReLU: \(h(z) = \max(0, z)\)

The perceptron is our building block. Simple alone, but powerful when combined in layers. Notice it’s just a linear combination followed by a nonlinearity.

Activation Functions Add Nonlinearity

Why Nonlinearity Matters

Without activation functions, stacking layers is pointless: \(f(\mathbf{W}_2 \mathbf{W}_1 \mathbf{x}) = f(\mathbf{W} \mathbf{x})\) where \(\mathbf{W} = \mathbf{W}_2\mathbf{W}_1\)

Later topic: Gradient flow and vanishing gradients during backpropagation

Closed-Form vs Iterative Optimization

Explicit (Closed-form)

\[\mathbf{w}^* = \arg\min_{\mathbf{w}} \|\mathbf{y} - \mathbf{X}\mathbf{w}\|^2\]

Solution: \[\mathbf{w}^* = (\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{y}\]

• One-shot computation
• Requires matrix inversion
• Memory intensive for large data

Iterative (Gradient-based)

\[\mathbf{w}_{t+1} = \mathbf{w}_t - \eta \nabla_{\mathbf{w}}\mathcal{L}(\mathbf{w}_t)\]

def sgd_step(w, x, y, learning_rate=0.01):
    prediction = np.dot(w, x)
    error = prediction - y
    gradient = error * x
    w_new = w - learning_rate * gradient
    return w_new

• Sequential updates
• Scales to large datasets
• Foundation of deep learning

While closed-form solutions exist for simple problems, gradient-based methods scale to millions of parameters and samples.

Gradient Descent Visualization

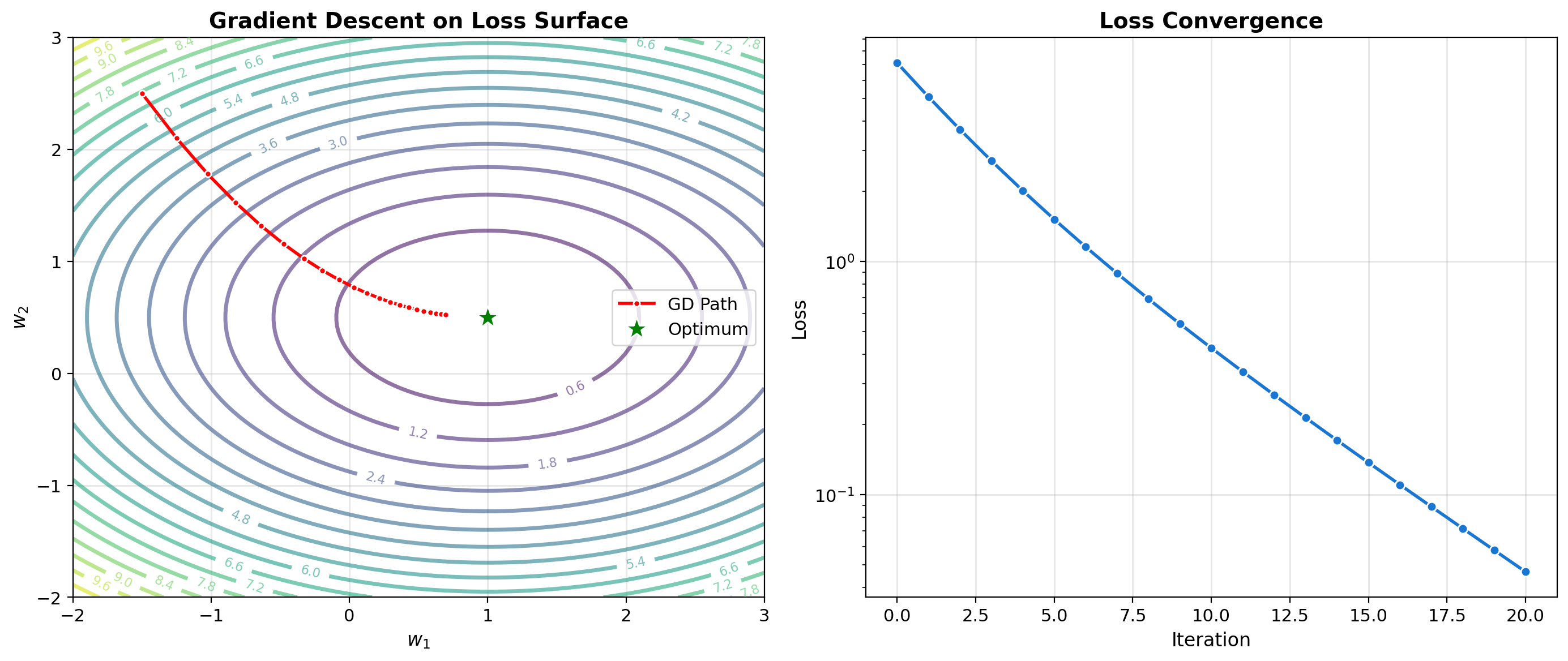
Iterative Optimization Principle

Gradient descent navigates the loss landscape by repeatedly moving in the direction of steepest descent. For convex problems, this guarantees convergence to the global minimum. For neural networks, we settle for local minima that generalize well.

This visualization shows gradient descent finding the minimum. In neural networks, the surface is much more complex but the principle remains.

The Bias-Variance Decomposition

Expected Prediction Error

\[\text{MSE} = \text{Bias}^2 + \text{Variance} + \sigma^2\]

Bias: Error from wrong model assumptions

• High bias: Model too simple (underfits)
• Low bias: Model captures true pattern

Variance: Error from sensitivity to training data

• High variance: Model memorizes noise (overfits)
• Low variance: Model finds generalizable pattern

Irreducible error (\(\sigma^2\)): Noise inherent in data

Tradeoff: Complex models reduce bias but increase variance

Bias-Variance in Practice: Polynomial Fitting

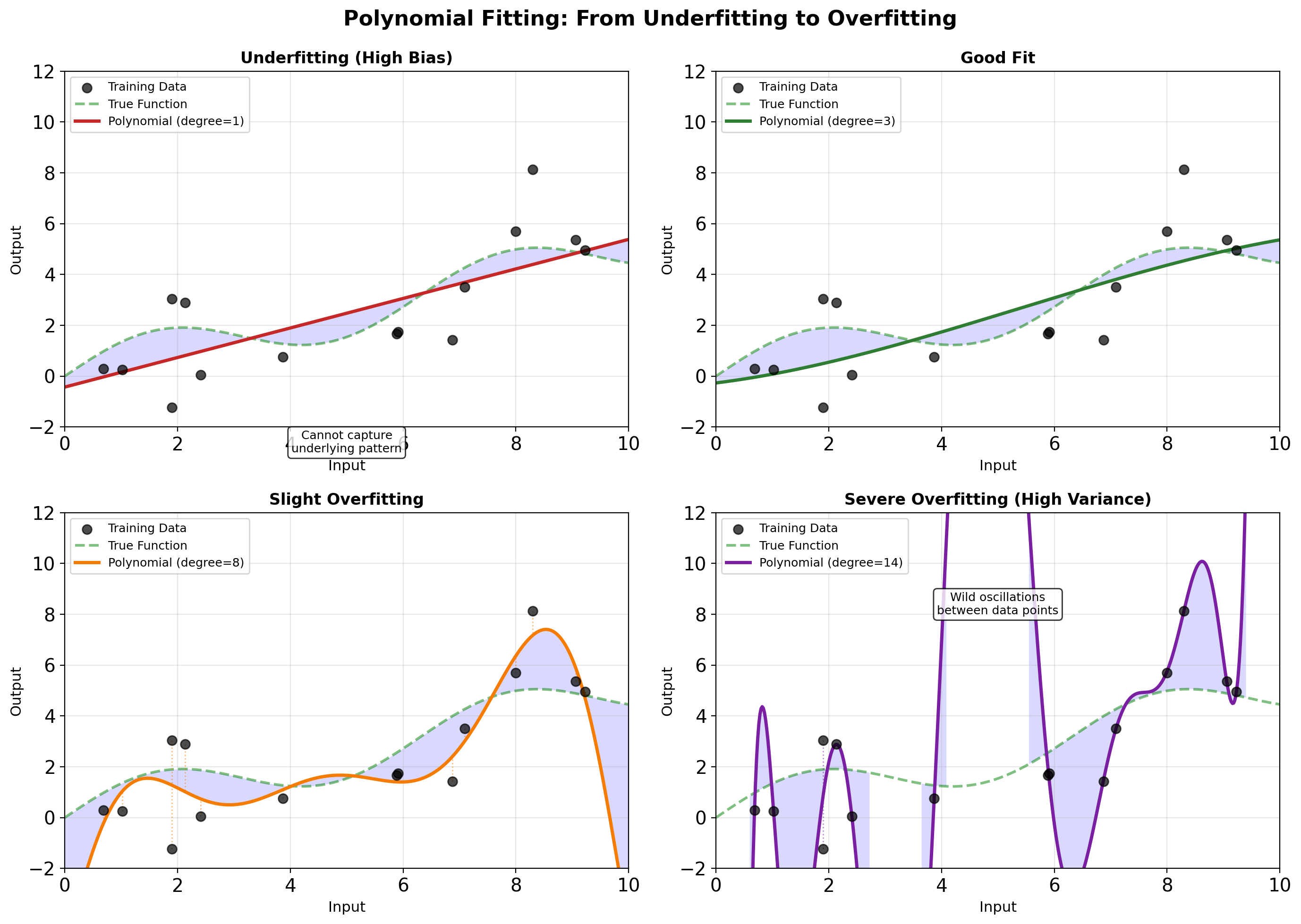
• Degree 1: Too simple, systematic error (high bias)
• Degree 3: Captures pattern without noise
• Degree 8: Starts fitting noise
• Degree 14: Wild oscillations (high variance)

Increasing complexity: bias decreases, variance increases

EE 541 Core Principles

Theory

1. Learning = Function Approximation

   • From data to predictions
   • Hypothesis class defines possibilities

2. Representation Matters

   • Same data, different encodings
   • Deep learning learns representations

3. Generalization is the Goal

   • Not memorization
   • Balance complexity with data

Implementation

1. Start Simple
   • Linear models as baselines
   • Add complexity purposefully
2. Iterate and Validate
   • Gradient descent scales
   • Monitor train vs test error
3. EE 541 Progression
   • MMSE → Regression → Neural Nets
   • Theory + PyTorch implementation

Listen to the Data

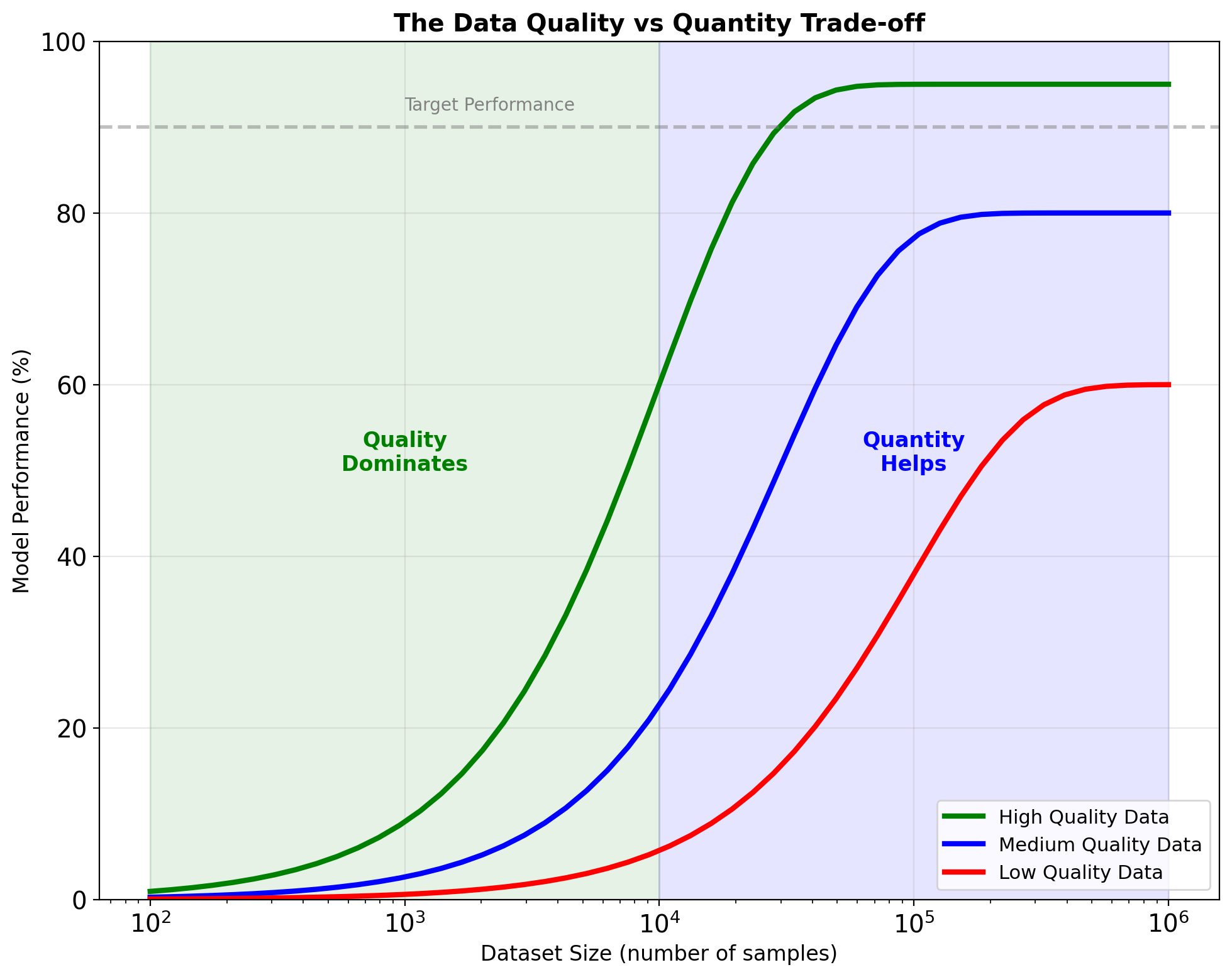
Data Quality Dominates Quantity

Clive Humby (2006)

“Data is the new oil”

But like oil, it must be refined to have value

\[\text{Model Performance} = f(\text{Data Quality}, \text{Data Quantity})\]

Illustrative Example: Data Refinement Impact

• Raw data: 10% usable (mislabeled, corrupted, outliers)
• Cleaned data: 40% usable (errors removed, imputed)
• Curated data: 90% usable (validated, balanced, relevant)

Note: Specific percentages vary by application, but quality improvement consistently outperforms quantity alone.

The “data is the new oil” analogy is apt - raw data, like crude oil, needs refinement to be valuable. Quality trumps quantity in most ML applications.

Representation Transforms Problem Difficulty

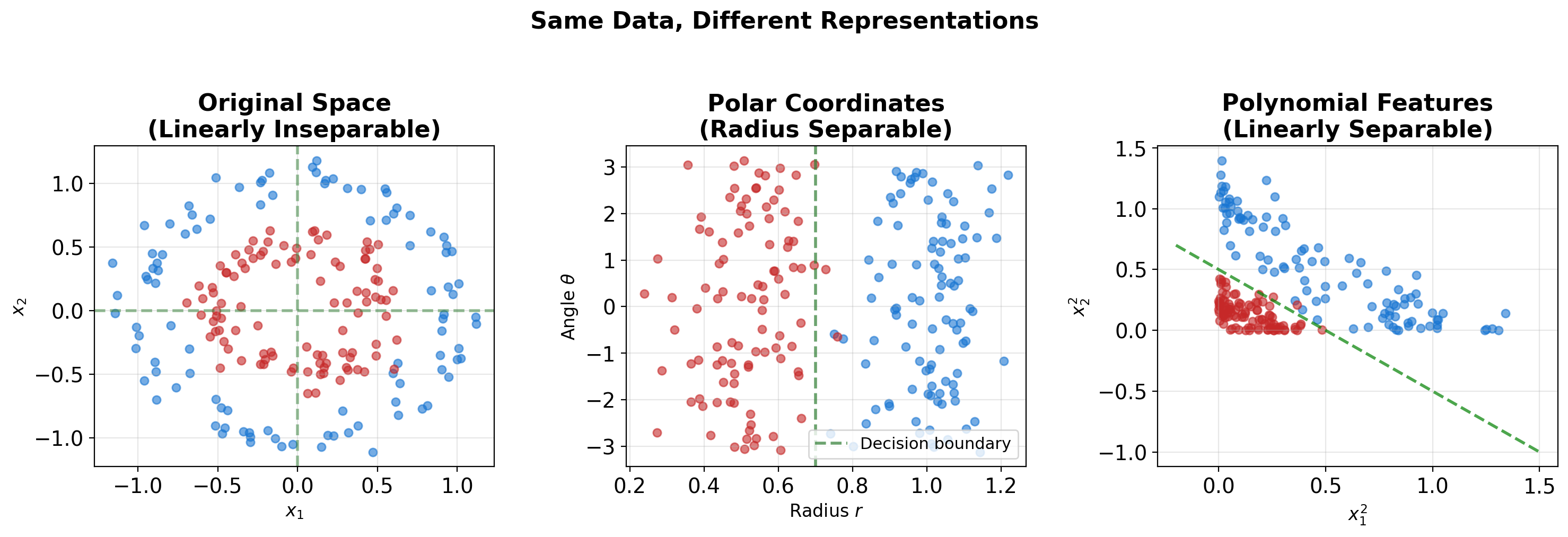
Representation Determines Learnability

Concentric circles: linearly inseparable in Cartesian coordinates, but trivially separable by radius in polar coordinates. Deep learning automates this search for effective representations.

This is why deep learning is powerful - it learns representations automatically rather than requiring manual feature engineering.

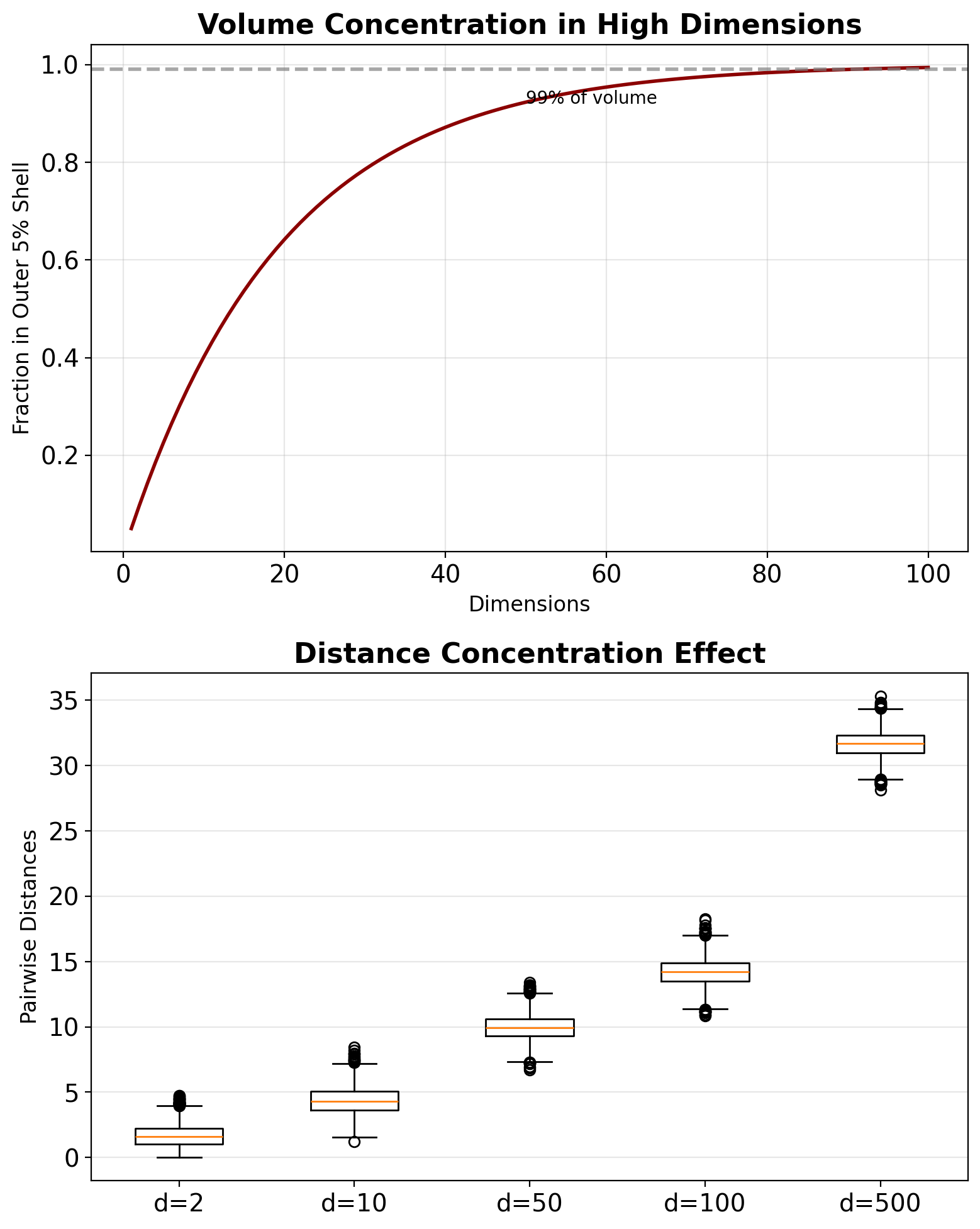
High Dimensions Break Geometric Intuition

The Curse of Dimensionality

As \(d \to \infty\):

• All points become equidistant
• Volume concentrates at surface
  
• Gaussian looks like uniform
• Nearest neighbors aren’t “near”

import numpy as np

def volume_ratio(d, epsilon=0.95):
    """Fraction of hypercube volume in outer shell"""
    return 1 - epsilon**d

dimensions = [1, 2, 3, 10, 100, 1000]
for d in dimensions:
    ratio = volume_ratio(d)
    print(f"d={d:4}: {ratio:.6f} in outer shell")

d=   1: 0.050000 in outer shell
d=   2: 0.097500 in outer shell
d=   3: 0.142625 in outer shell
d=  10: 0.401263 in outer shell
d= 100: 0.994079 in outer shell
d=1000: 1.000000 in outer shell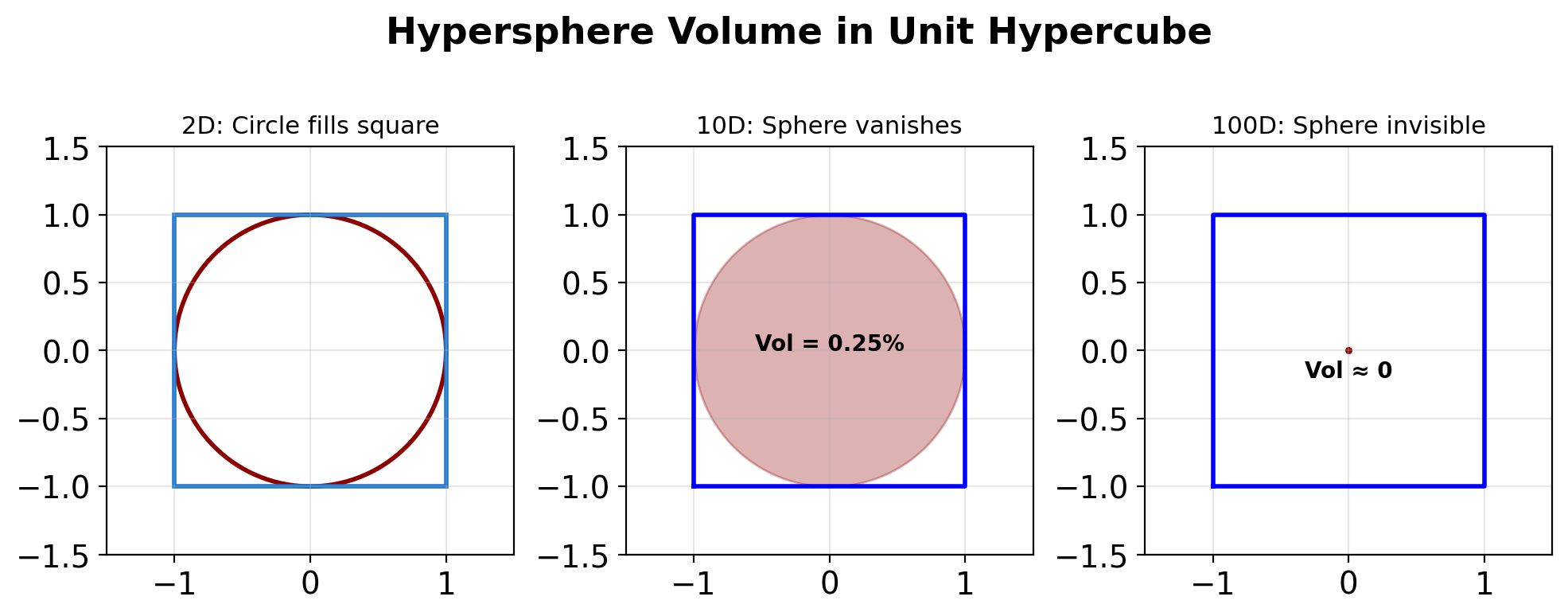

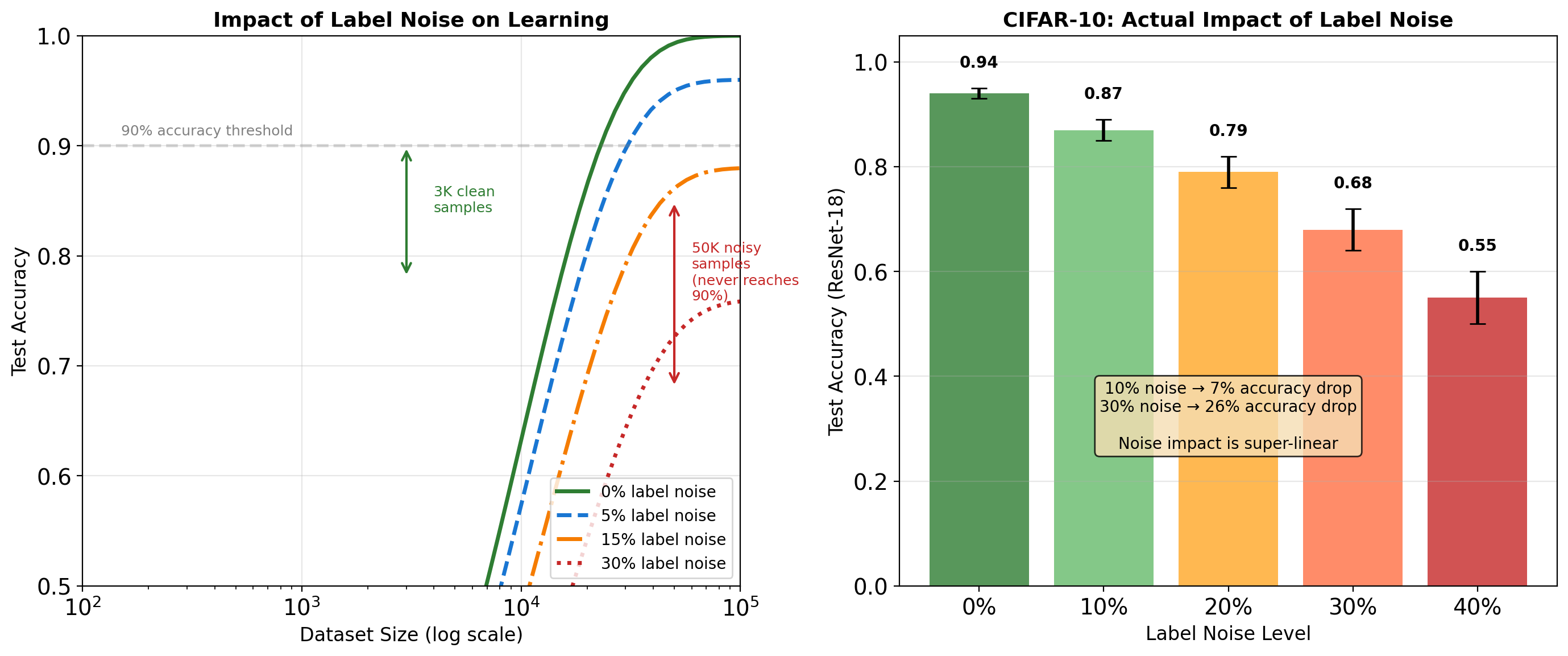
The curse of dimensionality is counter-intuitive but fundamental. In high dimensions, our geometric intuitions fail completely.

Label Noise Degrades Performance More Than Limited Data

Label noise creates an accuracy ceiling that cannot be overcome with more data. Clean data reaches high accuracy with far fewer samples than noisy data. This demonstrates why data curation and quality control are critical investments.

Amazon Resume Screening: Training on Biased Data

Setup (2014-2017):

• Train model on 10 years of hiring decisions
• Input: resumes → Output: 1-5 star rating
• Goal: automate screening for top candidates

What went wrong:

• Model penalized resumes with “women’s chess club”
• Model penalized graduates of all-women’s colleges
• Model learned patterns from biased historical data

The data:

Historical hires: 85% male, 15% female
Model learned: male-coded patterns = higher rating

System scrapped in 2018.

Why this matters:

The model did exactly what it was trained to do - replicate patterns in historical data.

The problem: historical data reflected real-world bias.

Clean data ≠ unbiased data

• Data was accurate (real hiring decisions)
• Data was complete (10 years of records)
• Data was biased (reflected industry demographics)

Data Augmentation: Synthetic Diversity from Limited Samples

Standard Augmentations

• Geometric: Rotation, flip, crop, scale
• Photometric: Brightness, contrast, color
• Noise: Gaussian, dropout, cutout
• Advanced: Mixup, CutMix, AutoAugment

Mathematical View

Training on augmented data: \[\min_\theta \sum_{i=1}^N \sum_{j=1}^M \mathcal{L}(f_\theta(T_j(x_i)), y_i)\]

where \(T_j\) are augmentation transforms

Data augmentation effectively multiplies your dataset size while encoding prior knowledge about invariances.

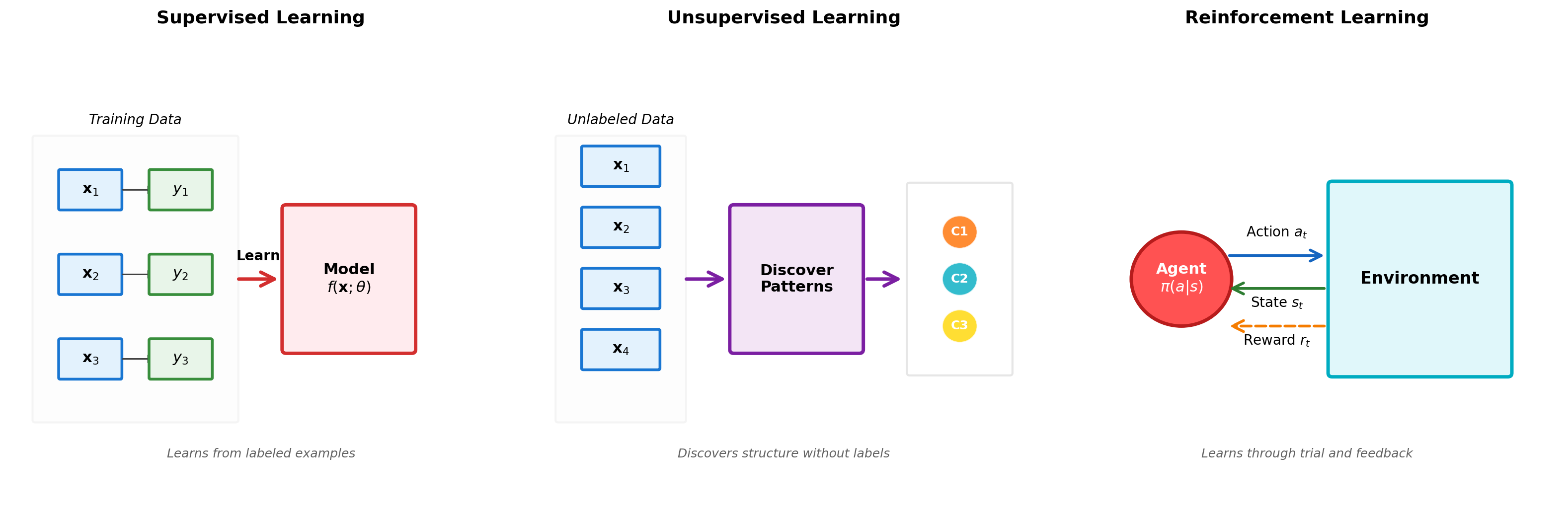
ML Learning Paradigms

Three Paradigms: Supervised, Unsupervised, Reinforcement

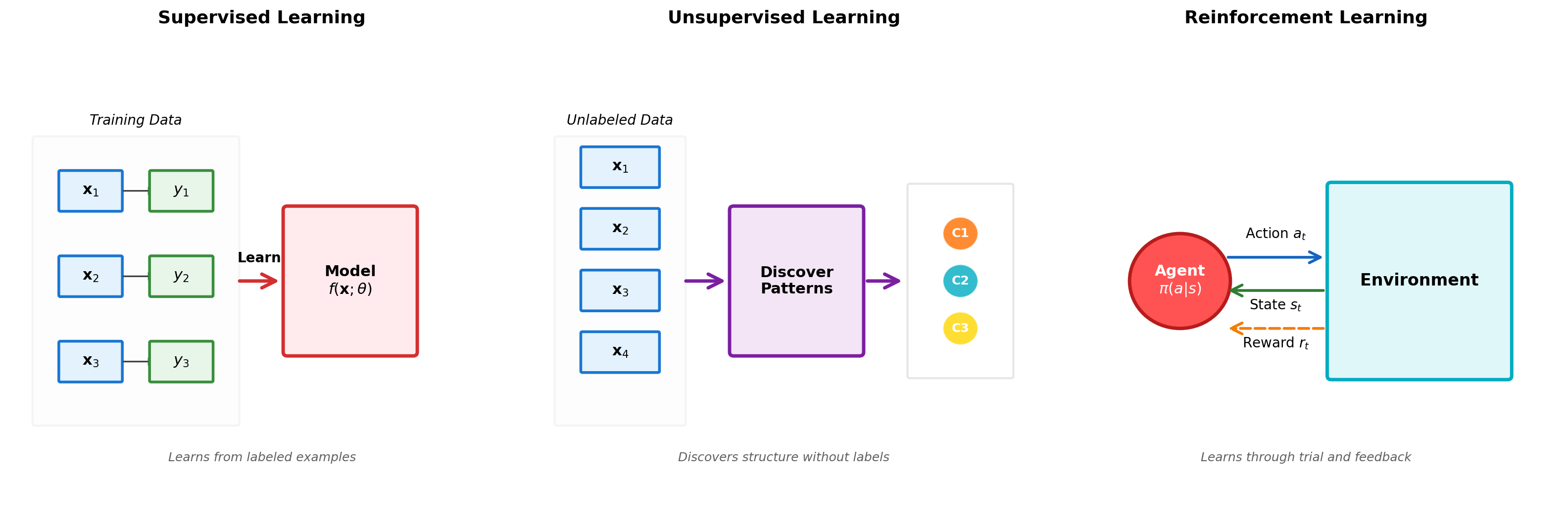
Modern methods combine paradigms: GPT-4 uses unsupervised pre-training on text, supervised fine-tuning on tasks, and reinforcement learning from human feedback (RLHF).

Three fundamental paradigms cover most of machine learning. Note that modern approaches often blur these boundaries.

Supervised Learning: Labeled Data to Function Mapping

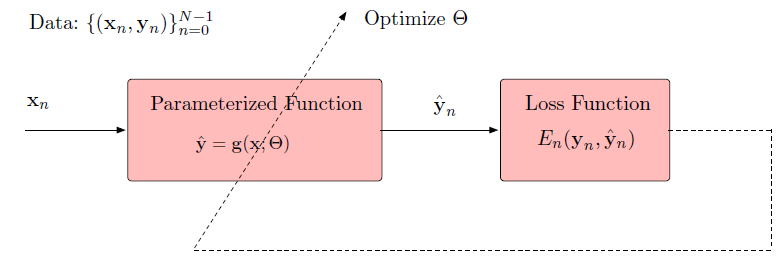
Problem Formulation

Given: \(\mathcal{D} = \{(\mathbf{x}_i, y_i)\}_{i=1}^N\)

Learn: \(f: \mathcal{X} \to \mathcal{Y}\)

Minimize: \(\mathcal{L}(f(\mathbf{x}), y)\)

Core Tasks

• Classification: \(y \in \{1, ..., C\}\)
• Regression: \(y \in \mathbb{R}^d\)
• Structured Prediction: \(y \in \mathcal{Y}_{\text{complex}}\)

Modern Applications

• Medical diagnosis from images
• Speech recognition
• Machine translation
• Time series forecasting

import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score

# Generate synthetic data
np.random.seed(42)
X = np.random.randn(1000, 10)
w_true = np.random.randn(10)
y = (X @ w_true + np.random.randn(1000)*0.1 > 0).astype(int)

# Standard supervised pipeline
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.2, random_state=42
)

model = LogisticRegression(max_iter=1000)
model.fit(X_train, y_train)

train_acc = accuracy_score(y_train, model.predict(X_train))
test_acc = accuracy_score(y_test, model.predict(X_test))

print(f"Train accuracy: {train_acc:.3f}")
print(f"Test accuracy: {test_acc:.3f}")

Train accuracy: 0.990
Test accuracy: 0.995

Supervised learning remains the workhorse of practical ML applications. Most production systems use supervised learning.

Supervised Learning Training and Inference

Linear Regression Task

Training Phase

Training Phase

Inference Phase

Inference Phase

A concrete example of supervised learning: linear regression. Given input-output pairs, learn the mapping function. The training phase involves learning from labeled examples, while inference applies the learned model to new data.

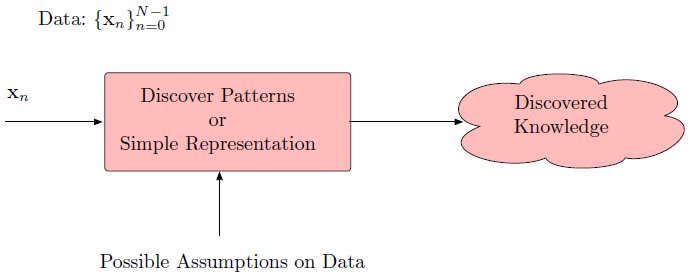
Unsupervised Learning: Structure from Unlabeled Data

No Labels, Just Data

Given: \(\mathcal{D} = \{\mathbf{x}_i\}_{i=1}^N\)

Find: Hidden patterns, structure, representations

Key Methods

• Clustering: K-means, DBSCAN, hierarchical
• Dimensionality Reduction: PCA, t-SNE, UMAP
• Density Estimation: GMM, KDE
• Representation Learning: Autoencoders

Unsupervised Learning System

Unsupervised learning is crucial for exploratory data analysis and learning representations without expensive labels.

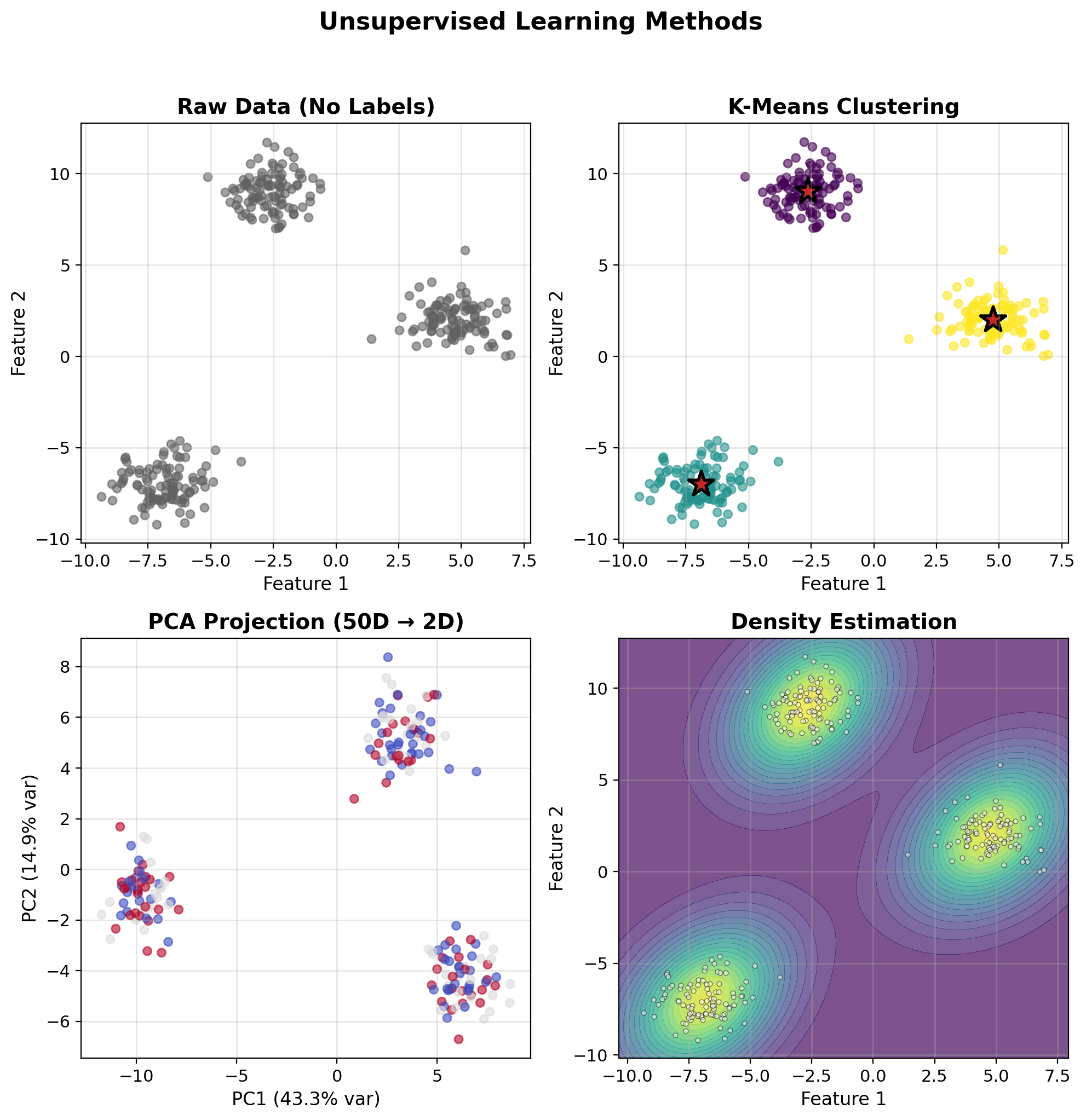
Clustering Reveals Hidden Patterns

Finding Structure in Data

Example of how unsupervised learning reveals hidden patterns - here showing clustering or dimensionality reduction revealing data structure.

Self-Supervised Learning: Labels from Data Itself

Creating Supervision from Data

Transform unsupervised → supervised by creating pretext tasks

Key Innovations

• Language Models: Predict next word (GPT)
• Masked Modeling: Predict masked parts (BERT)
• Contrastive Learning: Similar/different pairs (SimCLR)

Why It Works

• Unlimited labeled data (self-generated)
• Learns general representations
• Transfer learning to downstream tasks

# Example: Simple masked prediction
def create_masked_task(sequence, mask_prob=0.15):
    """Create self-supervised task from sequence"""
    masked = sequence.copy()
    labels = np.full_like(sequence, -1)
    
    mask_indices = np.random.random(len(sequence)) < mask_prob
    masked[mask_indices] = 0  # [MASK] token
    labels[mask_indices] = sequence[mask_indices]
    
    return masked, labels

# Example sequence
sequence = np.array([1, 4, 2, 8, 3, 7, 5, 9])
masked_input, targets = create_masked_task(sequence)

print(f"Original: {sequence}")
print(f"Masked:   {masked_input}")
print(f"Targets:  {targets}")

Original: [1 4 2 8 3 7 5 9]
Masked:   [1 0 0 0 3 0 5 9]
Targets:  [-1  4  2  8 -1  7 -1 -1]

Foundation Models and Self-Supervision

Self-supervised learning powers modern foundation models like GPT and BERT

Self-supervised learning has revolutionized NLP and is spreading to vision and other domains. It’s the key to foundation models.

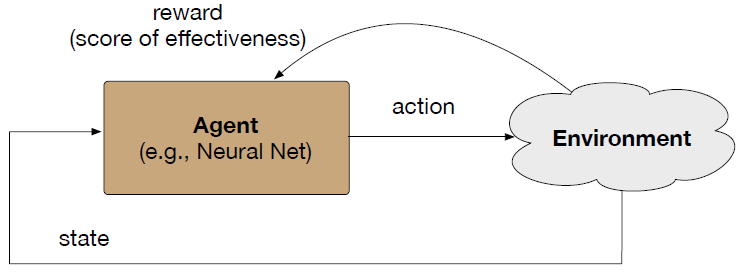
Reinforcement Learning: Sequential Decision Making

Sequential Decision Making

Components:

• State space: \(\mathcal{S}\)
• Action space: \(\mathcal{A}\)
  
• Reward function: \(R(s, a)\)
• Policy: \(\pi(a|s)\)

Objective: Maximize expected cumulative reward \[J(\pi) = \mathbb{E}_{\pi}\left[\sum_{t=0}^{\infty} \gamma^t r_t\right]\]

Applications

• Game playing (Chess, Go, StarCraft)
• Robotics control
• Resource allocation
• Trading strategies

RL is fundamentally different - it learns through interaction. Success in games has led to real-world applications in robotics and control.

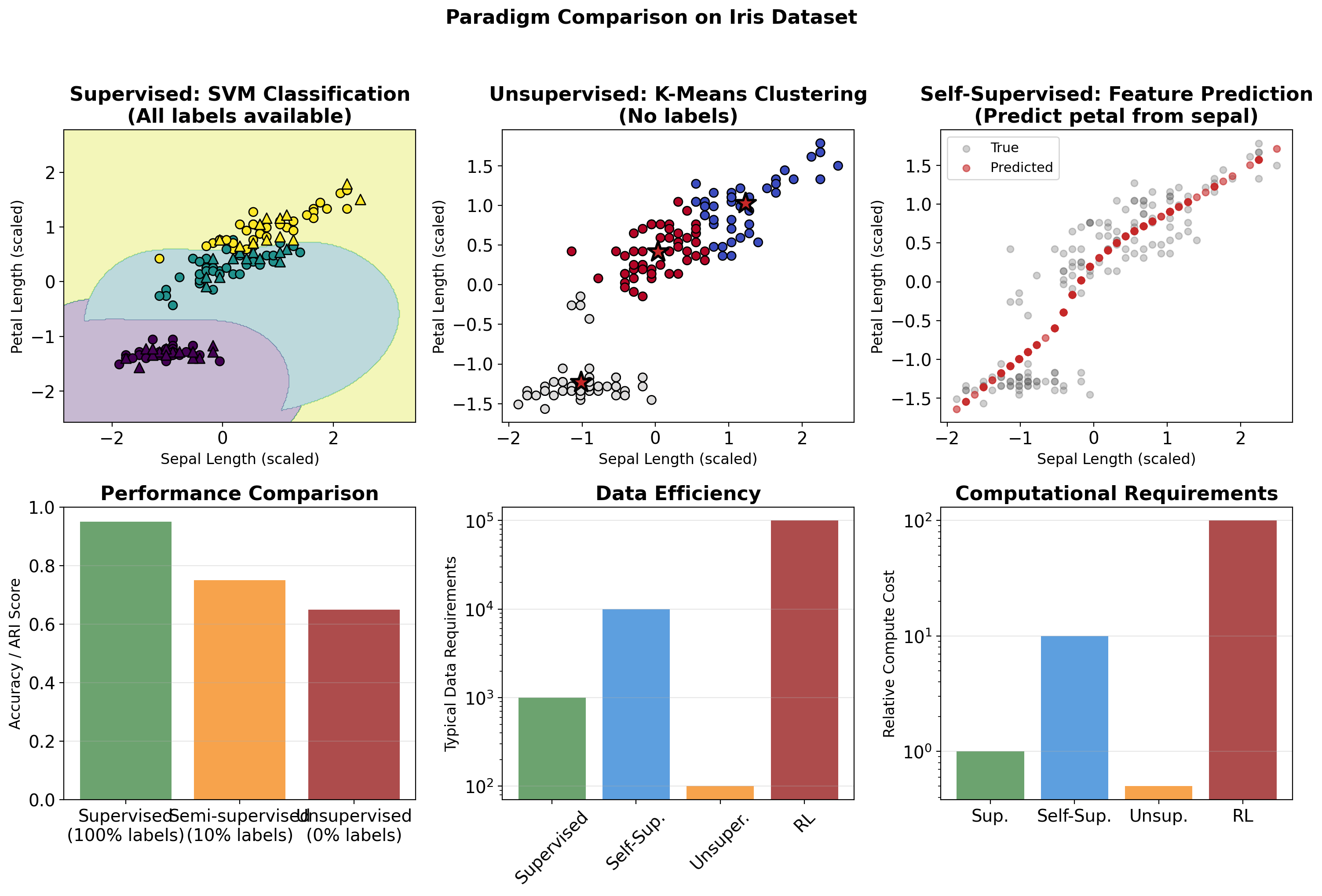
Same Problem, Different Paradigms

The same problem can be approached with different paradigms, each with trade-offs in terms of data requirements, computational cost, and performance.

Label efficiency on CIFAR-10 (target: 90% accuracy):

• Supervised (full labels): 50,000 labeled images
• Semi-supervised (10% labels): 5,000 labeled + 45,000 unlabeled
• Self-supervised pretraining + fine-tune: 1,000 labeled (after ImageNet pretraining)

Transfer learning with self-supervised pretraining: 50× reduction in labeled data

Modern Methods Combine Paradigms

Semi-Supervised Learning

• Use small labeled + large unlabeled data
• Pseudo-labeling, consistency regularization
• Example: FixMatch, MixMatch

Multi-Task Learning

• Learn multiple related tasks simultaneously
• Shared representations
• Example: BERT for multiple NLP tasks

Meta-Learning

• Learn to learn
• Few-shot adaptation
• Example: MAML, Prototypical Networks

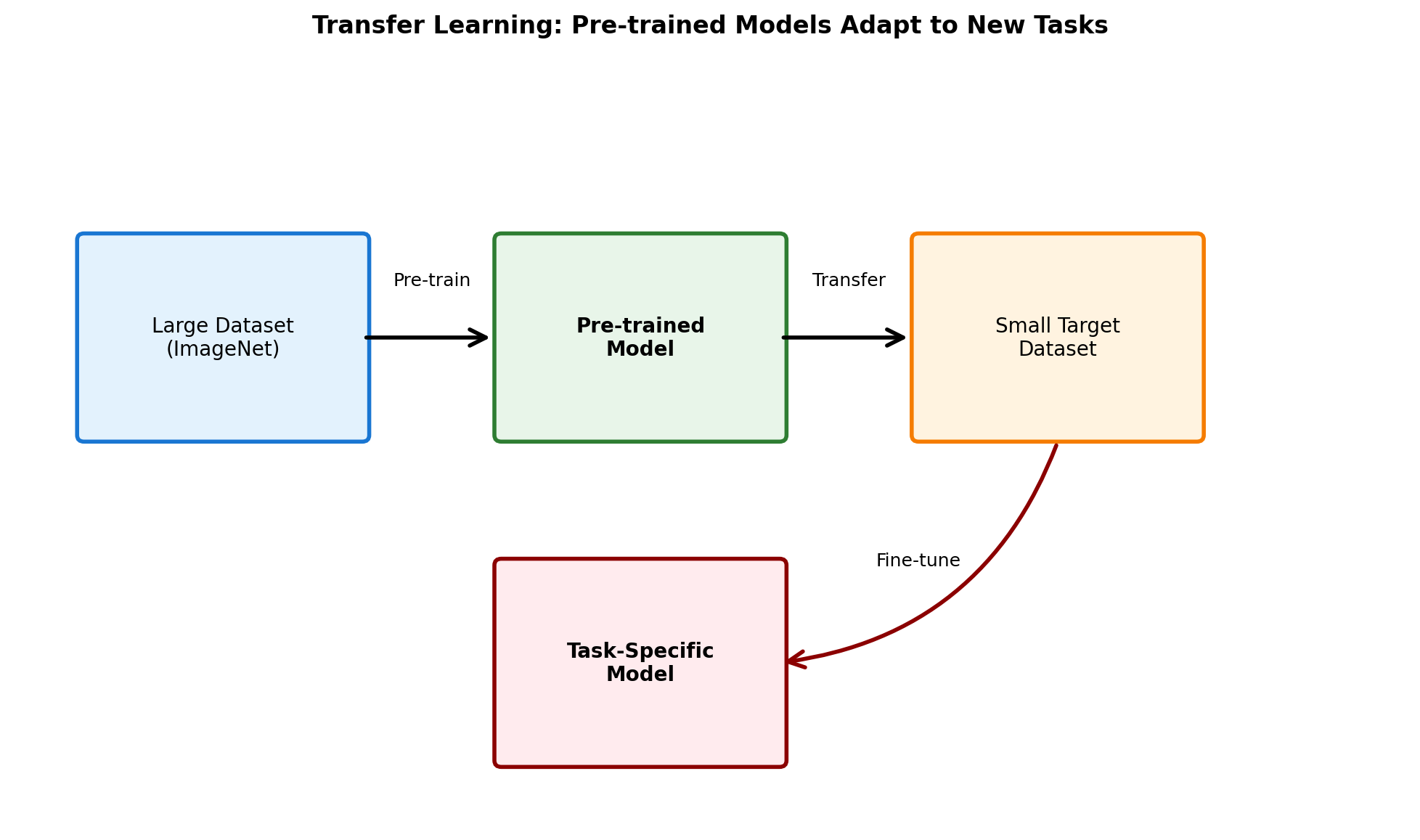
Transfer Learning Pipeline

Hybrid Learning Approaches

Modern approaches often combine paradigms for better performance

The boundaries between paradigms are increasingly blurred. Modern methods combine ideas from multiple paradigms.

Neural Architecture

Neural Networks Form a Rich Hypothesis Class

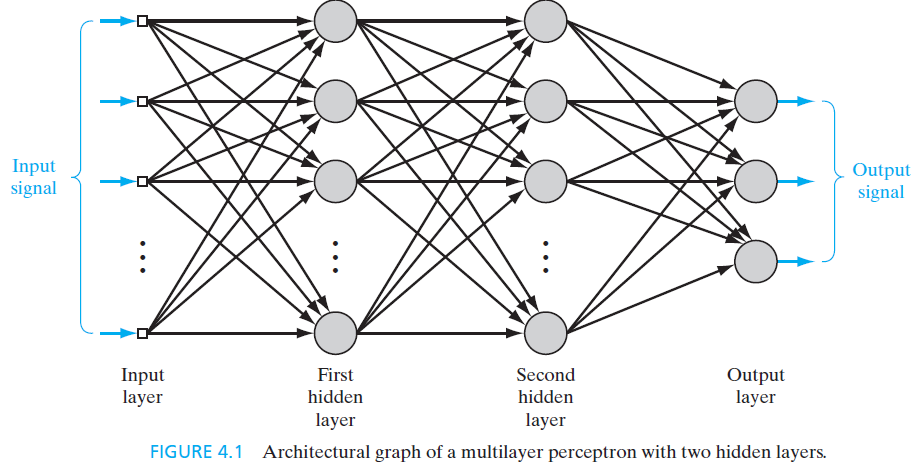
Multilayer Perceptron (MLP): Fully connected feedforward network

Architecture Components

• Input layer: Raw features \(\mathbf{x} \in \mathbb{R}^d\)
• Hidden layers: Learned representations
• Output layer: Task-specific predictions
• Connections: All-to-all between layers

Why “Rich” Hypothesis Class?

• Each neuron: Nonlinear transformation
• Composition: Exponential expressivity
• Universal approximation capability

Defn: Deep Neural Network

A neural network with more than one hidden layer. Depth enables hierarchical feature learning: early layers learn simple features, deeper layers learn complex abstractions.

The multilayer perceptron defines our fundamental architecture. Full connectivity means every neuron connects to all neurons in the next layer, creating a rich function space.

Single Neuron Computation

Forward Computation

At neuron \(i\) in layer \(l\):

\[a_i^{(l)} = h\left(\left[\mathbf{w}_i^{(l)}\right]^\top \mathbf{a}^{(l-1)} + b_i^{(l)}\right)\]

where:

• \(\mathbf{a}^{(l-1)}\): Previous layer activations
• \(\mathbf{w}_i^{(l)}\): Weight vector for neuron \(i\)
• \(b_i^{(l)}\): Bias term
• \(h(\cdot)\): Activation function

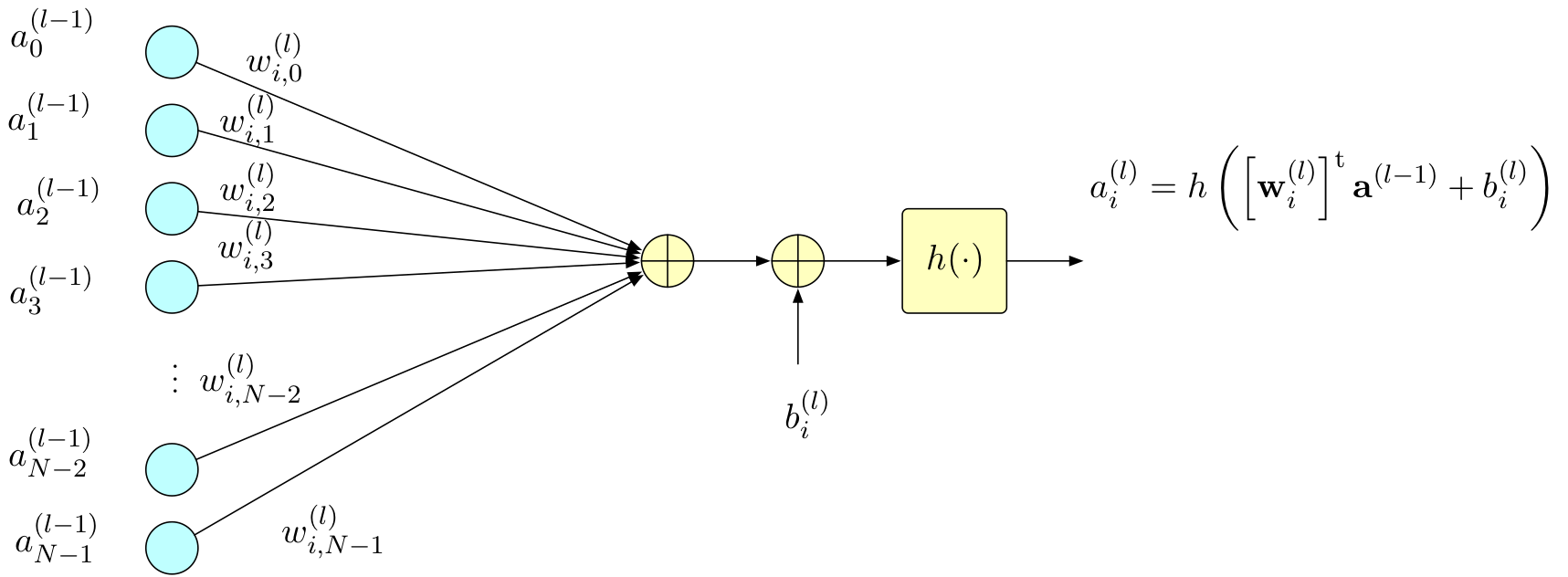
Matrix Form (Entire Layer)

\[\mathbf{a}^{(l)} = h\left(\mathbf{W}^{(l)} \mathbf{a}^{(l-1)} + \mathbf{b}^{(l)}\right)\]

• Parallelizes computation
• Enables GPU acceleration

This single neuron computation is the building block. Notice how matrix notation allows us to compute entire layers at once - critical for efficient implementation.

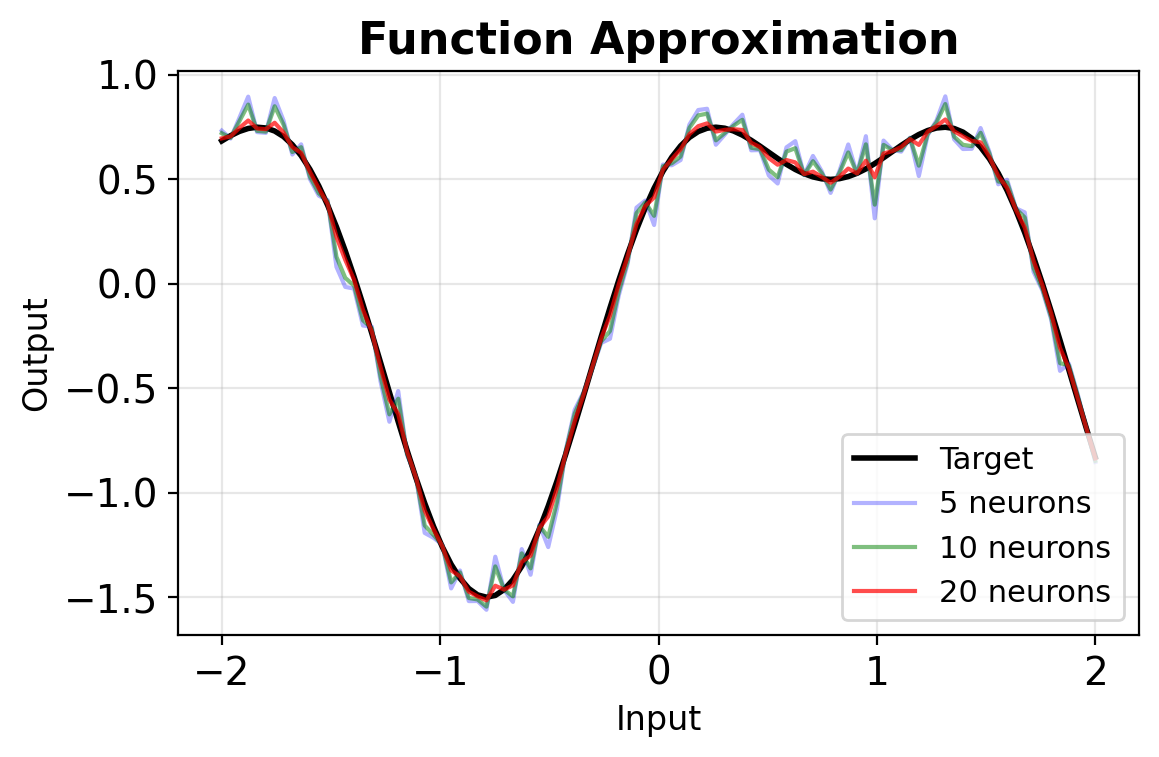
Universal Approximation: Existence Guarantee

Cybenko (1989), Hornik et al. (1989)

A feedforward network with:

• Single hidden layer
• Finite number of neurons
• Non-polynomial activation

can approximate any continuous function on compact subset of \(\mathbb{R}^n\) to arbitrary accuracy

Critical word: CAN

The theorem guarantees such networks exist. Finding them through training is different.

Preview

Detailed treatment later: approximation theory, width vs depth, practical training implications

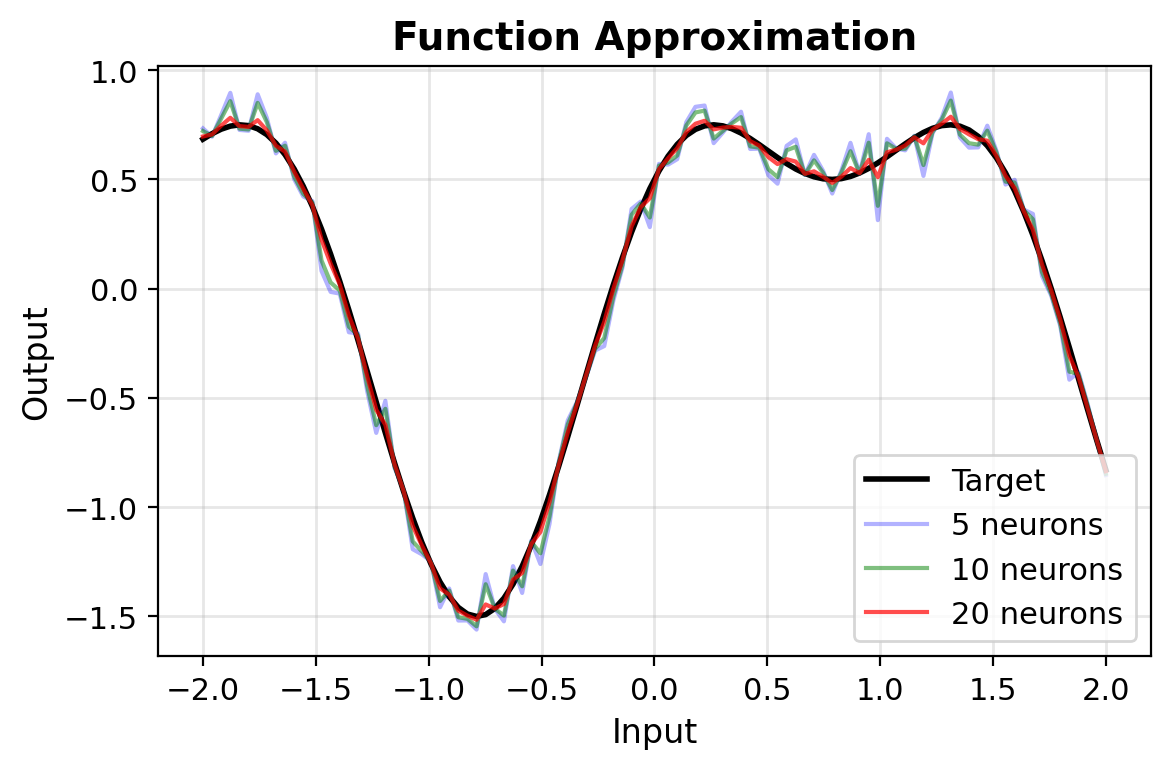
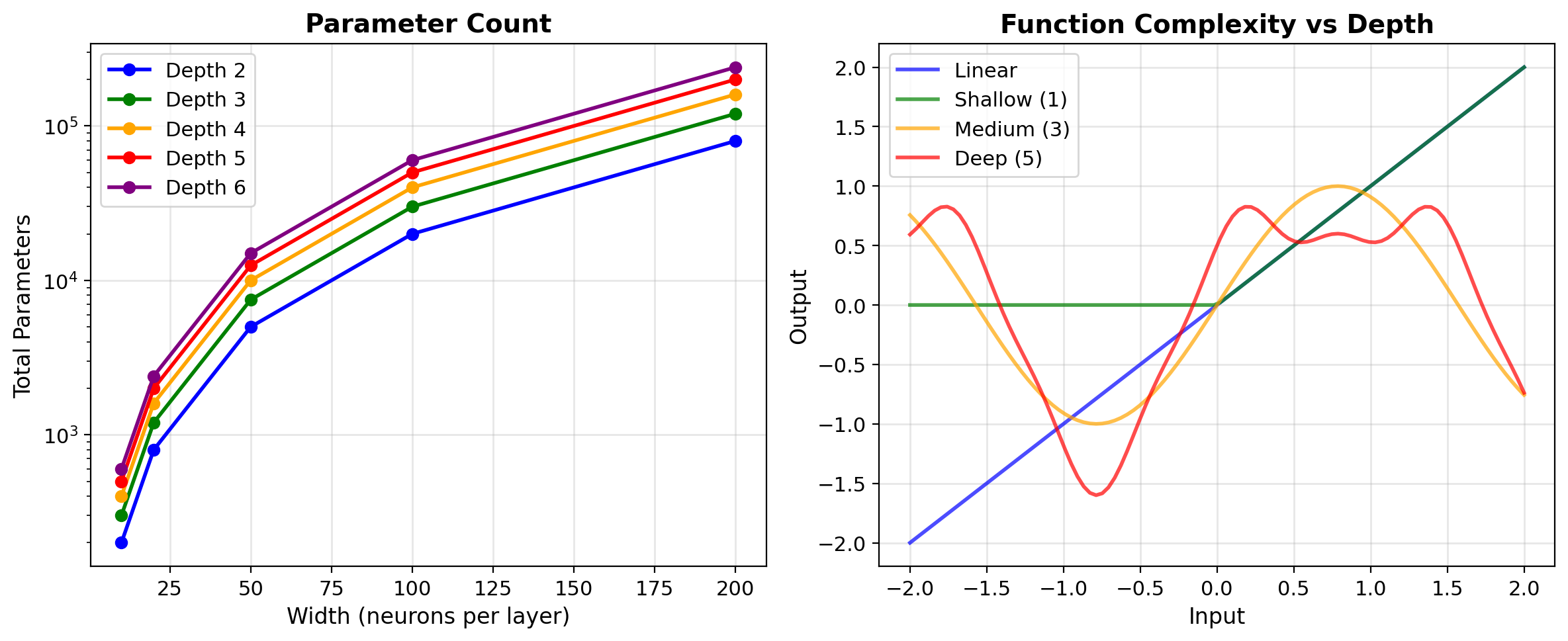
Width vs Depth: Why We Use Deep Networks

Width-only (single hidden layer)

Universal approximation guarantees this works, but:

• May require exponentially many neurons
• Example: parity function on n bits needs \(2^{n-1}\) hidden units
• Theorem says existence, not efficiency

Depth (multiple layers)

• More parameter-efficient representation
• Polynomial neurons vs exponential
• Hierarchical features emerge
• Same expressivity, fewer parameters

Why depth matters: Practical networks need efficient representations

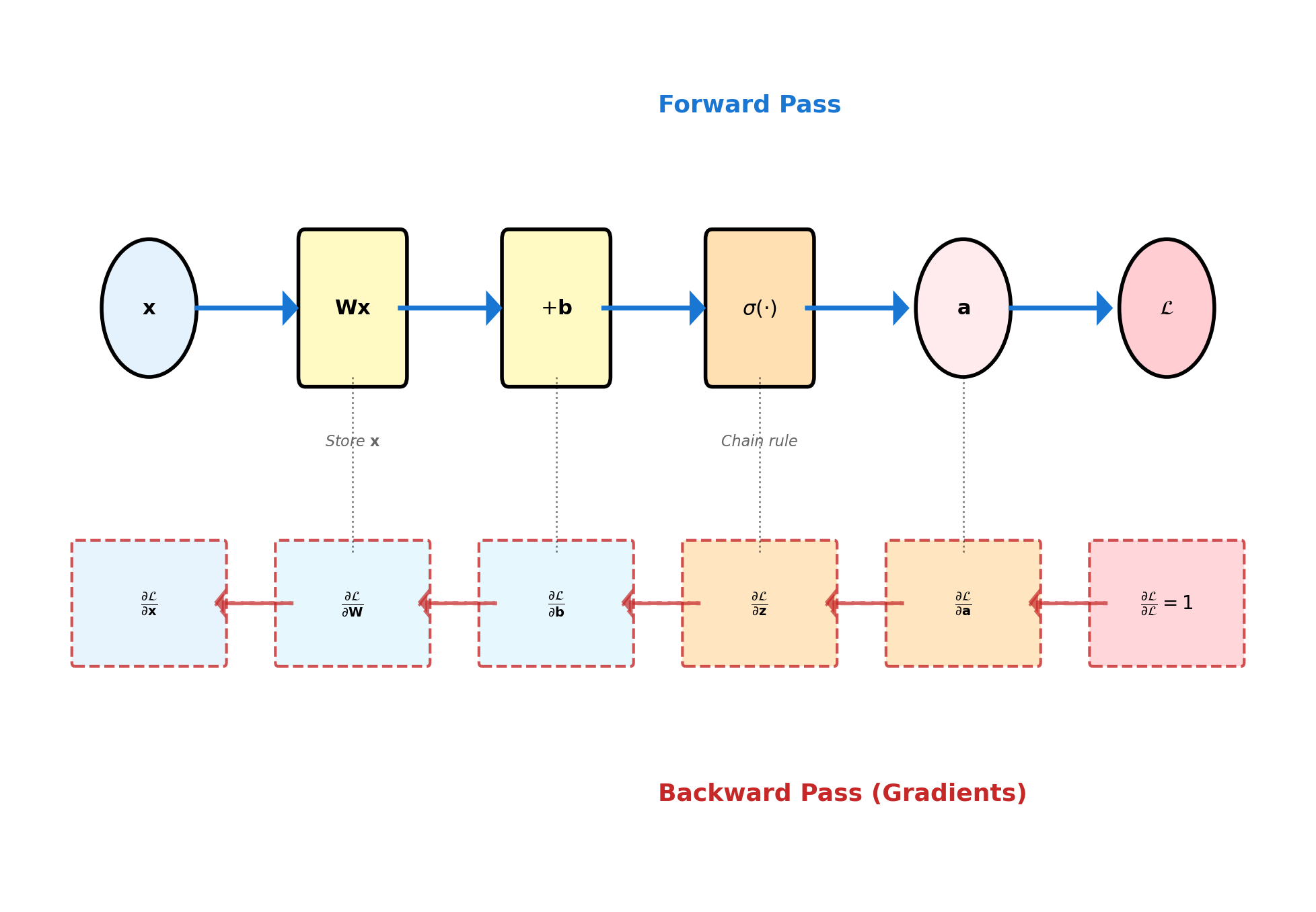
Forward and Backward Pass

Implementation

class Layer:
    def forward(self, x):
        # Store for backward pass
        self.x = x
        # Linear transformation
        self.z = np.dot(x, self.W) + self.b
        # Apply activation
        self.a = self.activation(self.z)
        return self.a
    
    def backward(self, grad_output):
        # Chain rule through activation
        grad_z = grad_output * \
                 self.activation_derivative(self.z)
        
        # Parameter gradients
        self.grad_W = np.dot(self.x.T, grad_z)
        self.grad_b = np.sum(grad_z, axis=0)
        
        # Input gradient for previous layer
        grad_input = np.dot(grad_z, self.W.T)
        return grad_input

Computational Graph

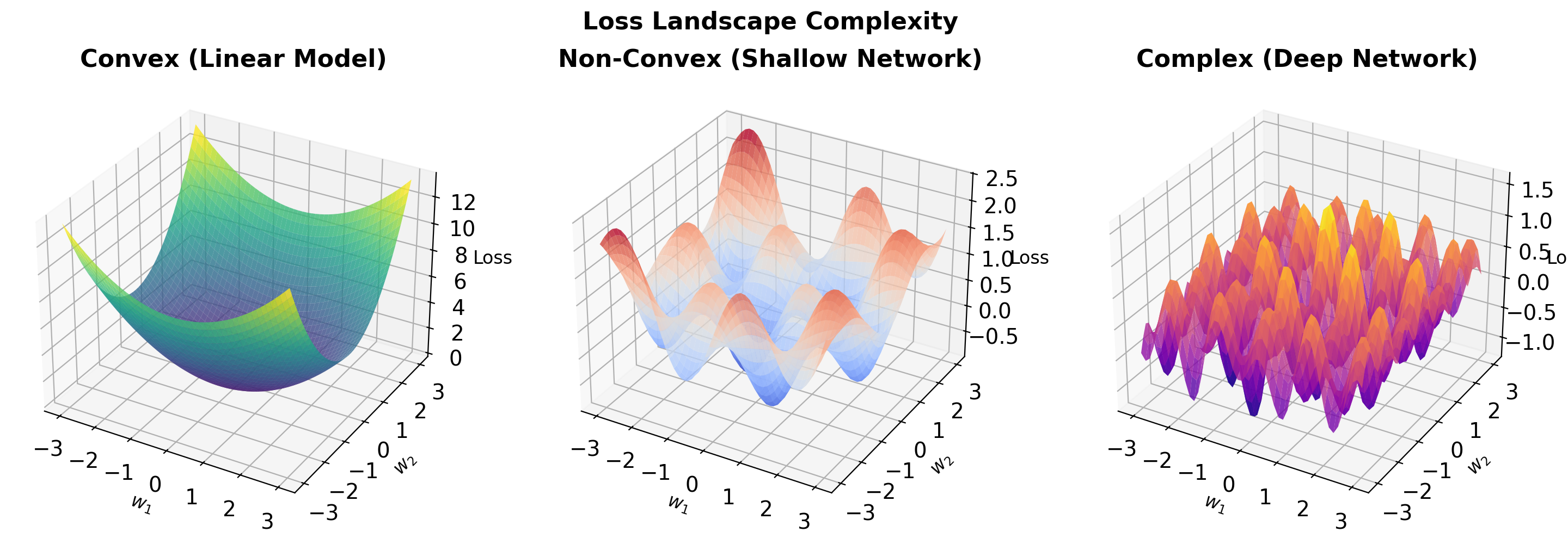
Network Capacity and Depth

Depth provides exponential expressivity gains. Each layer learns increasingly abstract features.

The Optimization Landscape

Loss Surfaces in High Dimensions

Mathematical Reality

In \(d\) dimensions with \(n\) parameters:

• Critical points: \(\mathcal{O}(e^n)\)
• Most are saddle points, not local minima
• Minima often connected by low-loss paths

Empirical Observations

• Loss landscapes are surprisingly well-behaved
• Wide networks have smoother landscapes
  
• Overparameterization helps optimization
• Mode connectivity phenomenon

The high-dimensional loss landscape is far more benign than low-dimensional intuition suggests. Saddle points dominate over local minima.

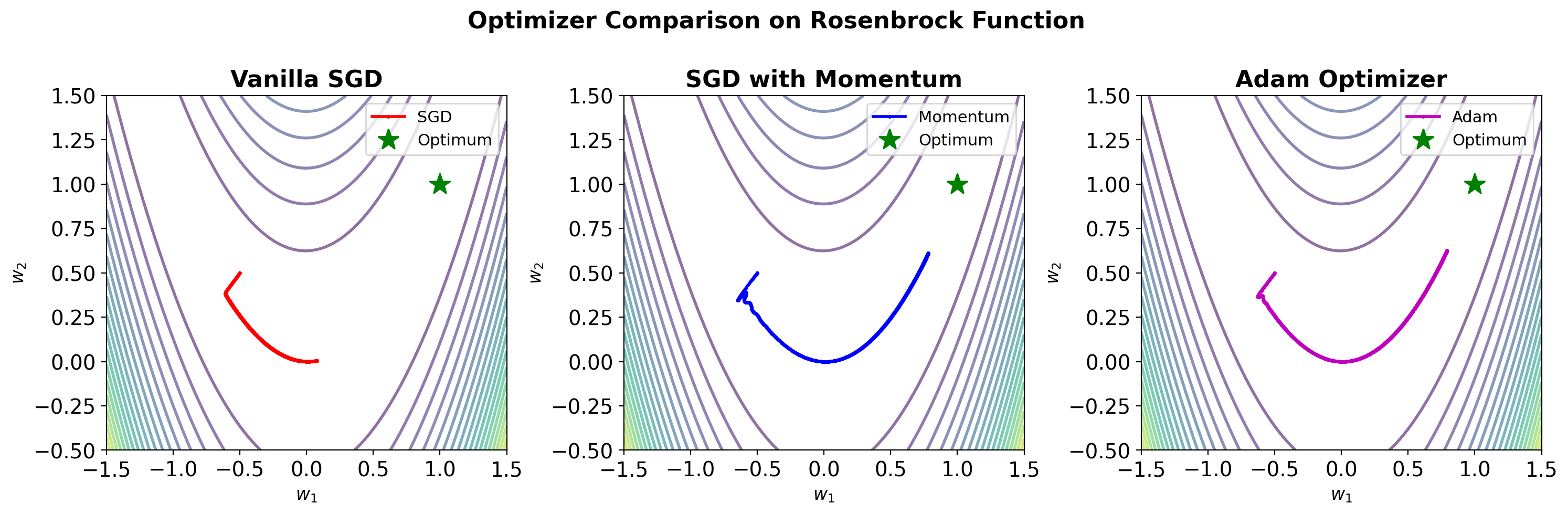
Stochastic Gradient Descent and Variants

def sgd(w, grad, lr=0.01):
    return w - lr * grad

def sgd_momentum(w, grad, velocity, lr=0.01, beta=0.9):
    velocity = beta * velocity + lr * grad
    return w - velocity, velocity

def adam(w, grad, m, v, t, lr=0.001, beta1=0.9, beta2=0.999, eps=1e-8):
    m = beta1 * m + (1 - beta1) * grad
    v = beta2 * v + (1 - beta2) * grad**2
    m_hat = m / (1 - beta1**t)
    v_hat = v / (1 - beta2**t)
    return w - lr * m_hat / (np.sqrt(v_hat) + eps), m, v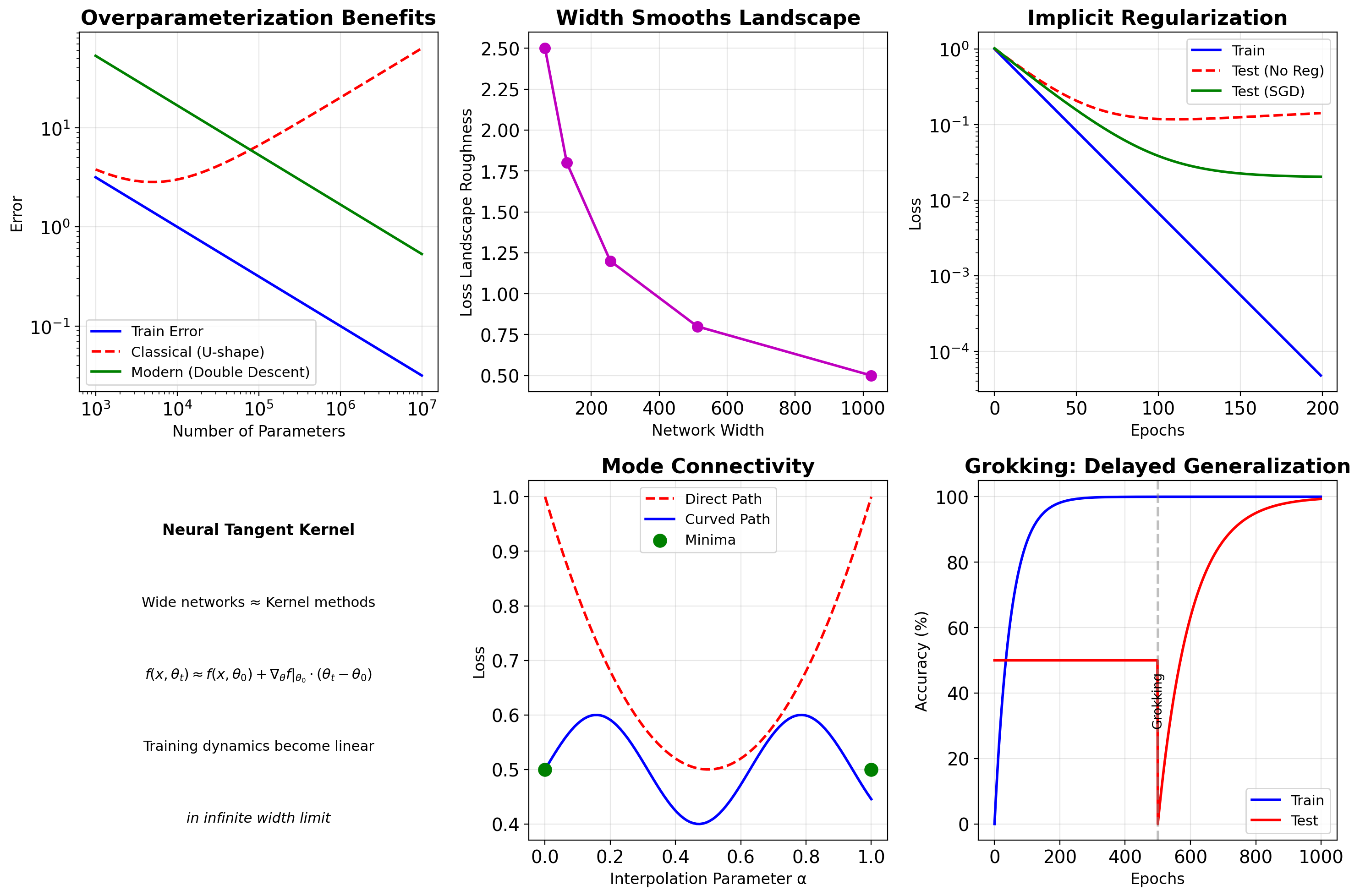

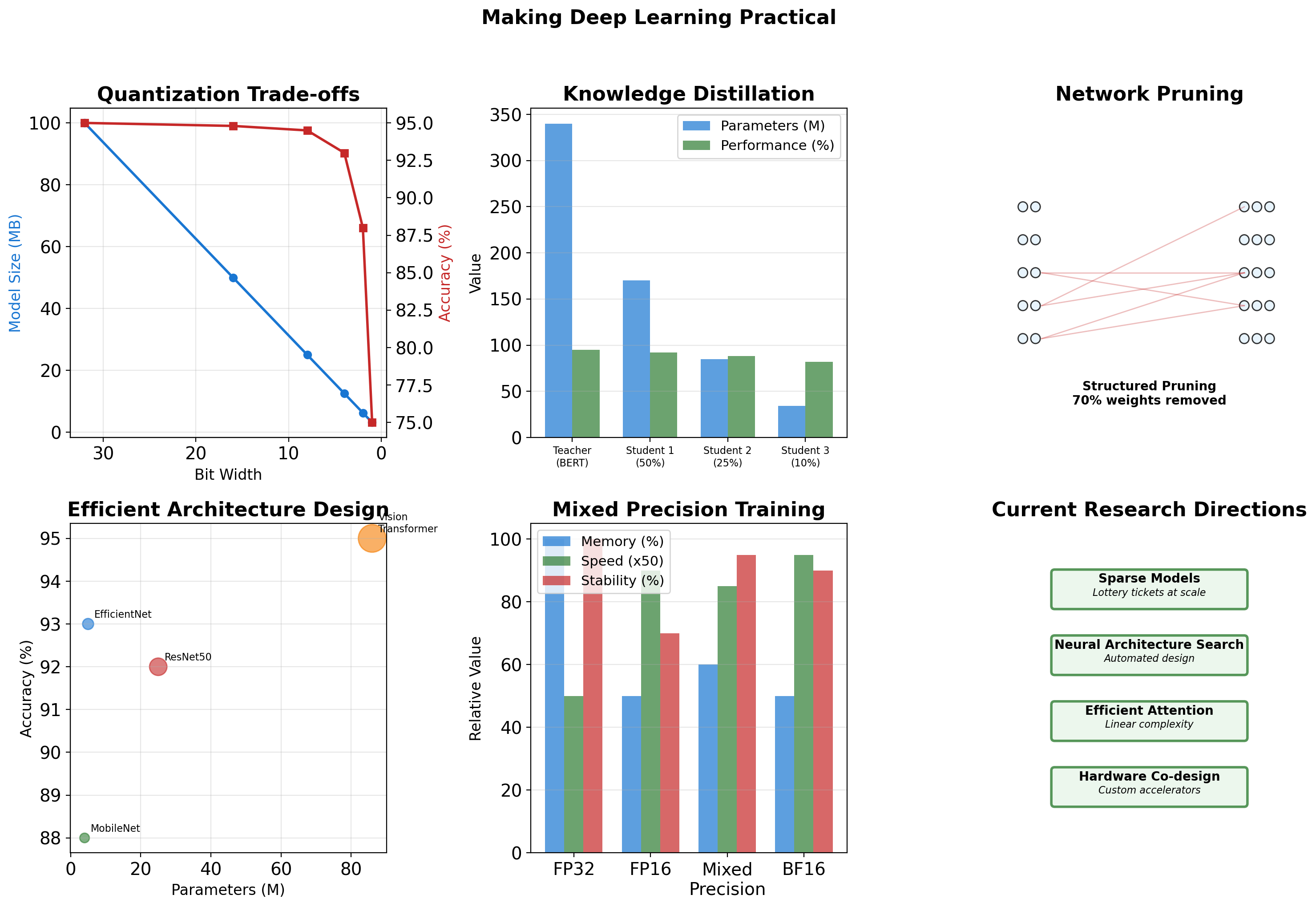
Different optimizers navigate the loss landscape differently. Adam’s adaptive learning rates help in complex landscapes.

Lottery Ticket Hypothesis: Sparse Subnetworks at Initialization

Frankle & Carbin (2019)

“Dense networks contain sparse subnetworks that can train to comparable accuracy from the same initialization”

Implications

• Networks are vastly overparameterized
• Winning tickets exist at initialization
• Pruning can maintain performance
• Structure matters more than we thought

Practical Impact

\[\text{Parameters: } 100M \to 10M\] \[\text{Performance: } 95\% \to 94.5\%\]

Why this matters:

Storage:

• 100M: ~400MB (too large for mobile)
• 10M: ~40MB (fits on phone)

Speed:

• 100M: ~100ms per image
• 10M: ~10ms per image (real-time)

Training:

• 100M: 5 days on single GPU
• 10M: 12 hours (faster experiments)

Detailed treatment: Network pruning and efficient architectures

The lottery ticket hypothesis reveals that successful training depends on finding the right sparse subnetwork within the dense initialization.

Modern Theoretical Insights

Recent theory shows that overparameterization, far from being problematic, actually helps optimization and generalization through various mechanisms.

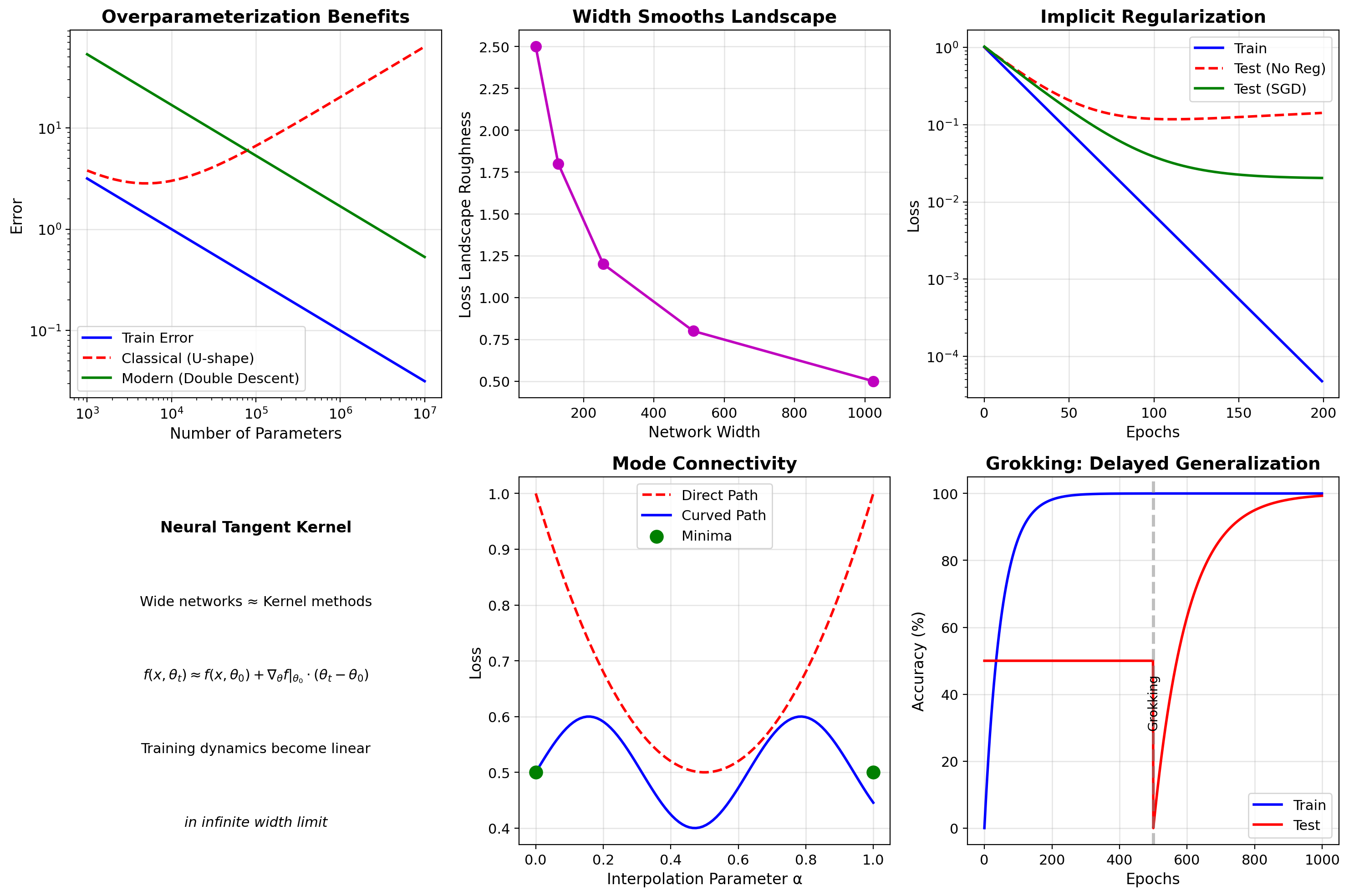
Why Deep Networks Generalize

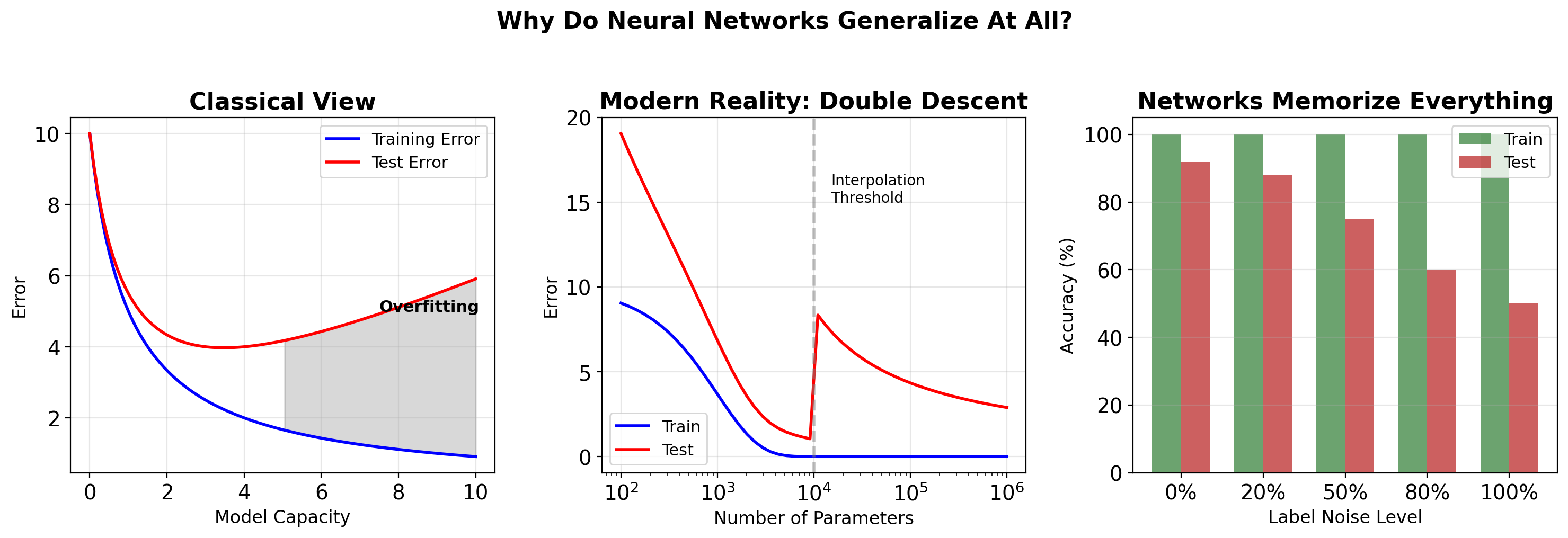
Neural Networks Memorize Random Labels Yet Generalize on Real Data

Neural networks can perfectly memorize random labels yet still generalize on real data. This violates classical learning theory.

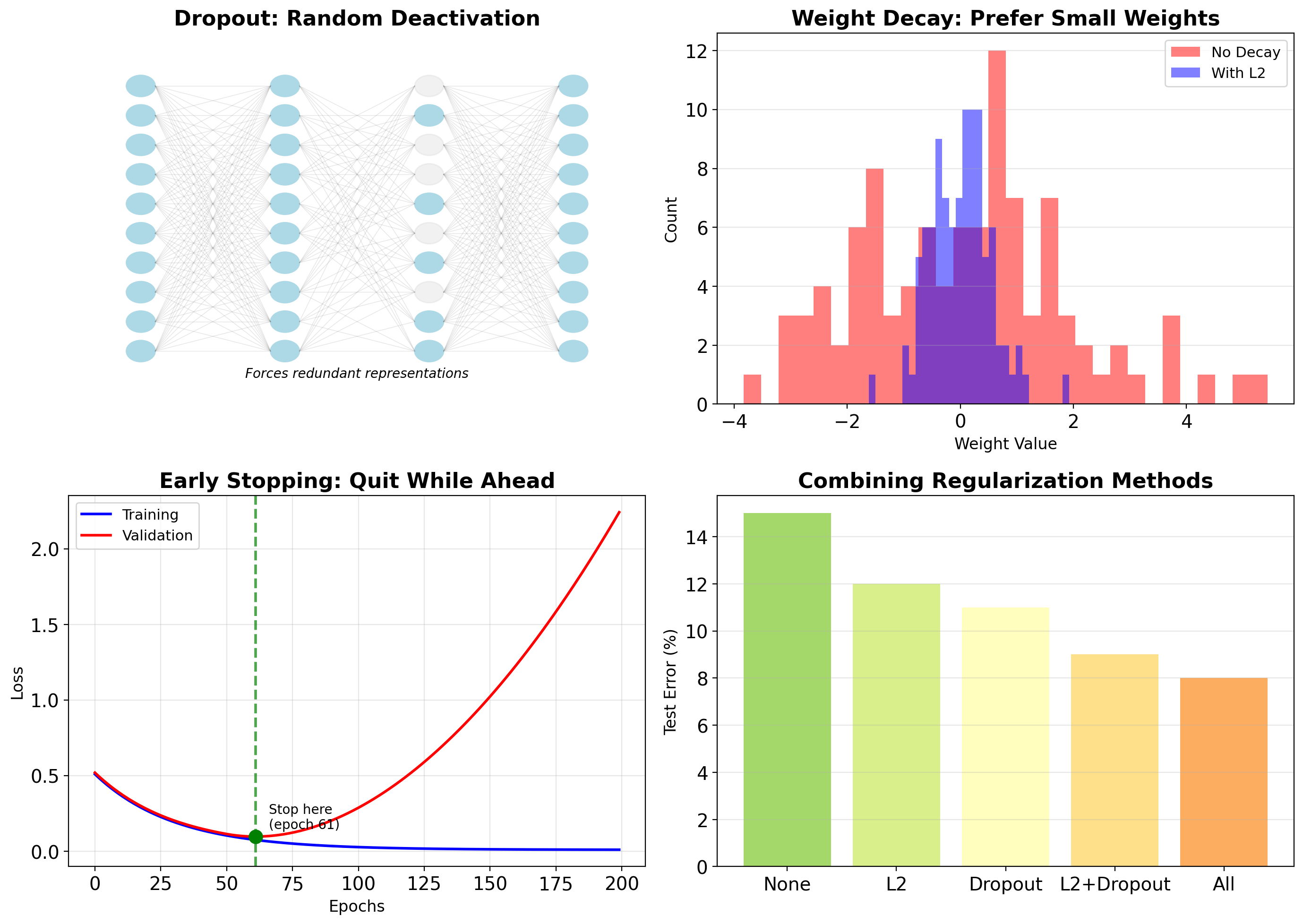
Regularization Techniques: Dropout and Weight Decay

def dropout(x, p=0.5, training=True):
    if not training:
        return x
    mask = np.random.binomial(1, 1-p, size=x.shape) / (1-p)
    return x * mask

def weight_decay(loss, weights, lambda_reg=0.01):
    l2_penalty = sum(np.sum(w**2) for w in weights)
    return loss + lambda_reg * l2_penalty

Regularization methods constrain the hypothesis space, but the real mystery is why SGD finds generalizing solutions without explicit regularization.

Architecture Embeds Domain Knowledge

Architecture choice embeds assumptions about the problem. CNNs assume spatial locality, RNNs assume temporal dependencies.

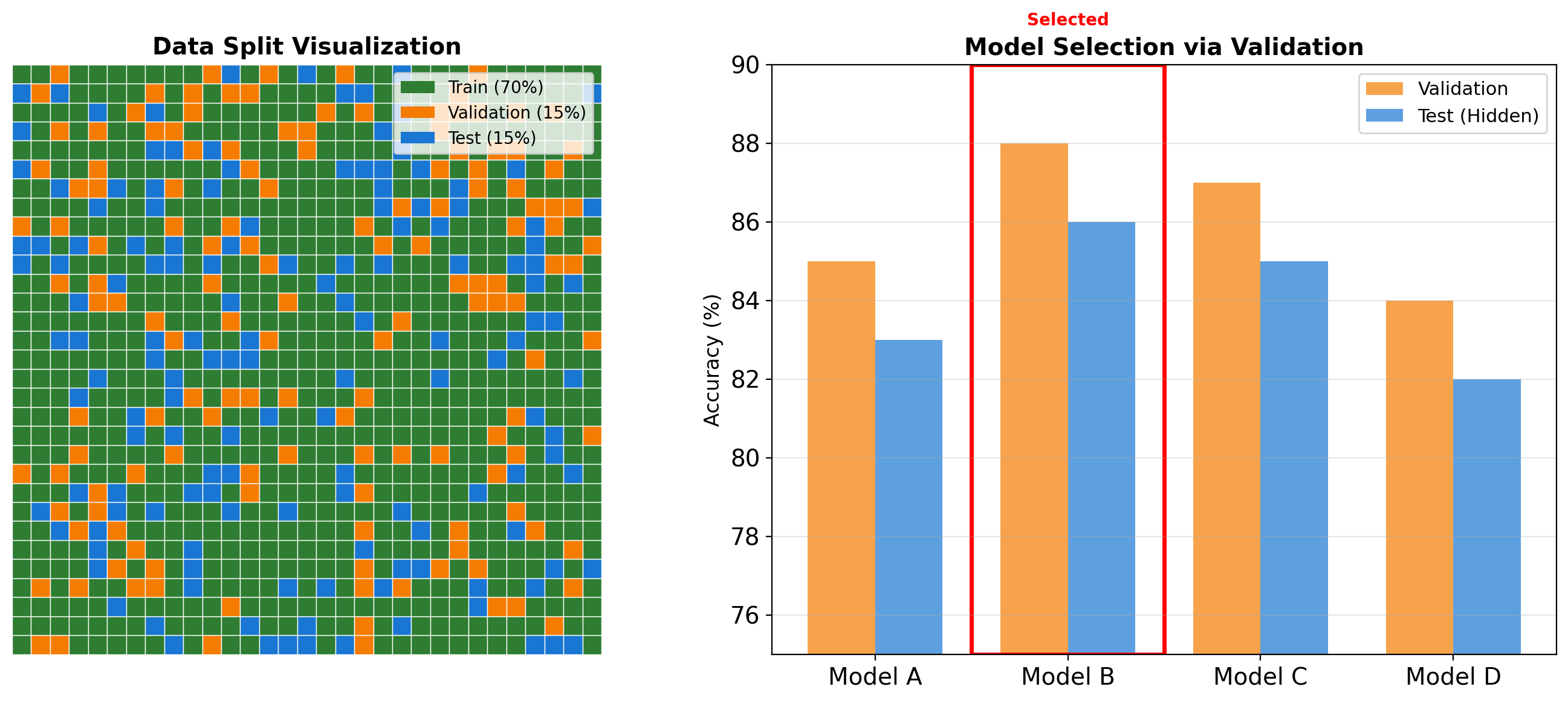
Train/Validation/Test: Sacred Separation

WARNING: Data Contamination

Never touch test data until final evaluation - validation data guides all decisions

The train/validation/test split is sacred. Validation guides hyperparameter tuning, test measures final generalization.

Generalization Remains Partially Unexplained

What We Don’t Understand

Why does SGD find generalizing solutions?
Networks can memorize random labels perfectly,
yet SGD finds patterns when labels are real

Why does overparameterization help?
10x more parameters than samples should overfit,
but often improves test accuracy

What is the role of depth?
Shallow wide networks have same capacity,
but deep networks generalize better

How do transformers generalize?
No convolutions, no recurrence,
yet state-of-the-art on vision and language

Note: No single theory fully explains deep learning generalization. Active research area.

Despite practical success, our theoretical understanding of why deep learning generalizes remains incomplete. This is an active research area.

Zillow Home Pricing: When the World Changes

Setup (2018-2021):

• Predict home values for algorithmic buying
• Train on 2018-2020 housing data
• Validation: 95% accurate (within 5% of price)
• Test set: 94% accurate
• Model looked excellent

Deployment (2021):

• COVID shifts housing market
• Model systematically underpredicts by $80K-$100K
• Loss: $500M+ before shutting down

What happened:

Training data came from stable market. Deployment happened during rapid market shift. Model kept predicting pre-COVID prices.

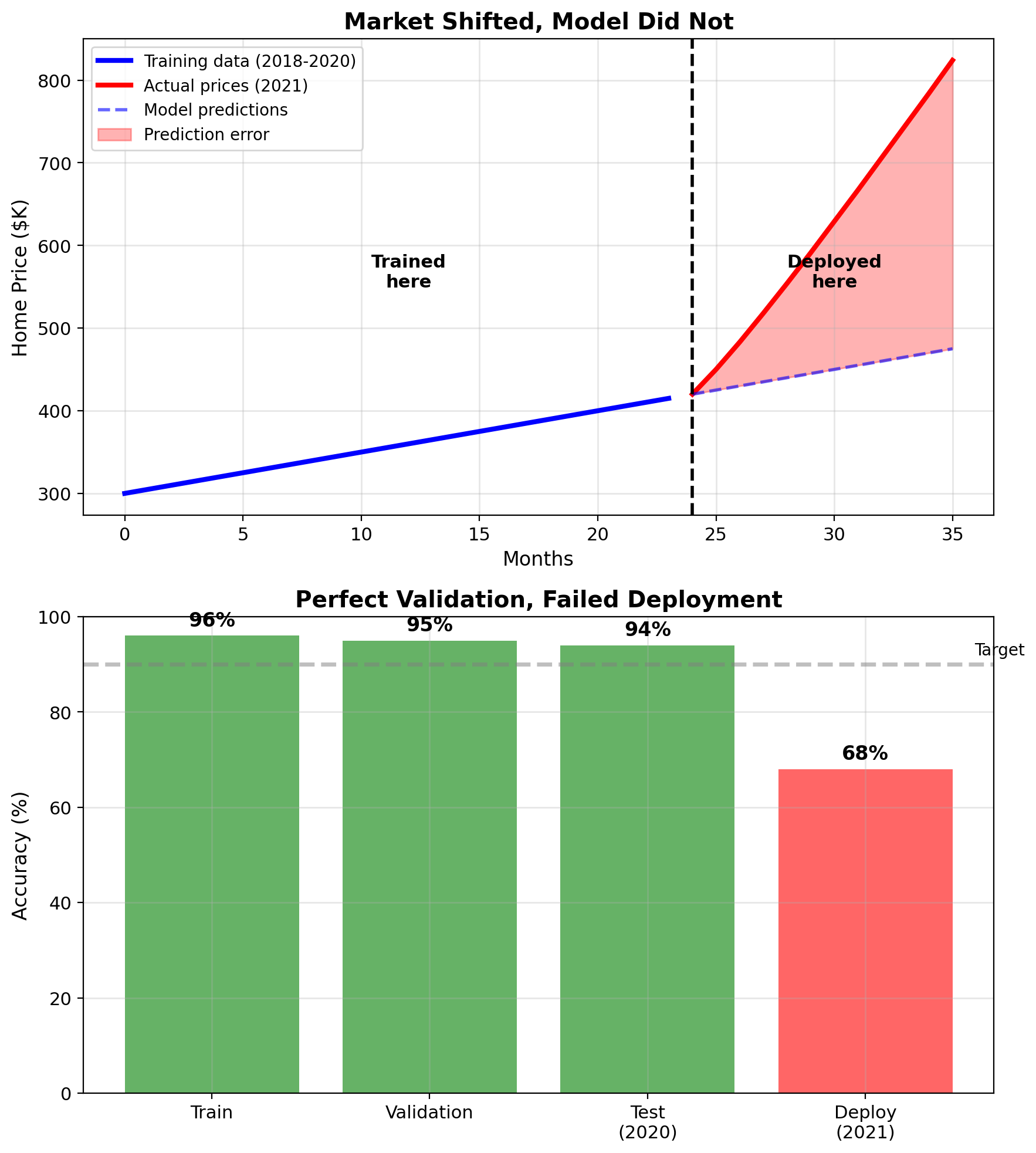
The problem:

All your validation tools assume the future looks like the past. When the world changes, models trained on historical data fail.

Train/val/test all from 2018-2020: Model learns pre-COVID patterns
Deploy in 2021: COVID changed everything
Result: Model is wrong, but doesn't know it's wrong

This is not a rare edge case - markets shift, user behavior changes, new products emerge. Distribution shift is common.

Building Systems Despite Incomplete Theory

What theory doesn’t fully explain

• Why SGD finds generalizing solutions (not just any minimum)
• How overparameterization helps (contradicts classical theory)
• What depth contributes beyond expressivity
• Why some architectures work better than others

Classical theory predicts

• More parameters than data causes overfitting
• Zero training error means poor generalization
• Simpler models should always win

Modern practice shows

• Overparameterized networks generalize well
• Zero training loss often gives best test performance
• Complex models frequently outperform simple ones

How we build systems anyway

Empirical validation:

• Train/validation/test splits (always)
• Monitor generalization gap continuously
• Trust validation performance over theory

Defensive engineering:

• Start simple, add complexity gradually
• Regularize by default (dropout, weight decay)
• Early stopping when validation degrades
• Ensemble multiple models for robustness

Course approach:

• Learn techniques that work empirically
• Understand intuition for why they might work
• Recognize when theory provides guarantees
• Know when you’re operating without guarantees

Many fundamental questions remain open research problems.

Modern Deep Architectures

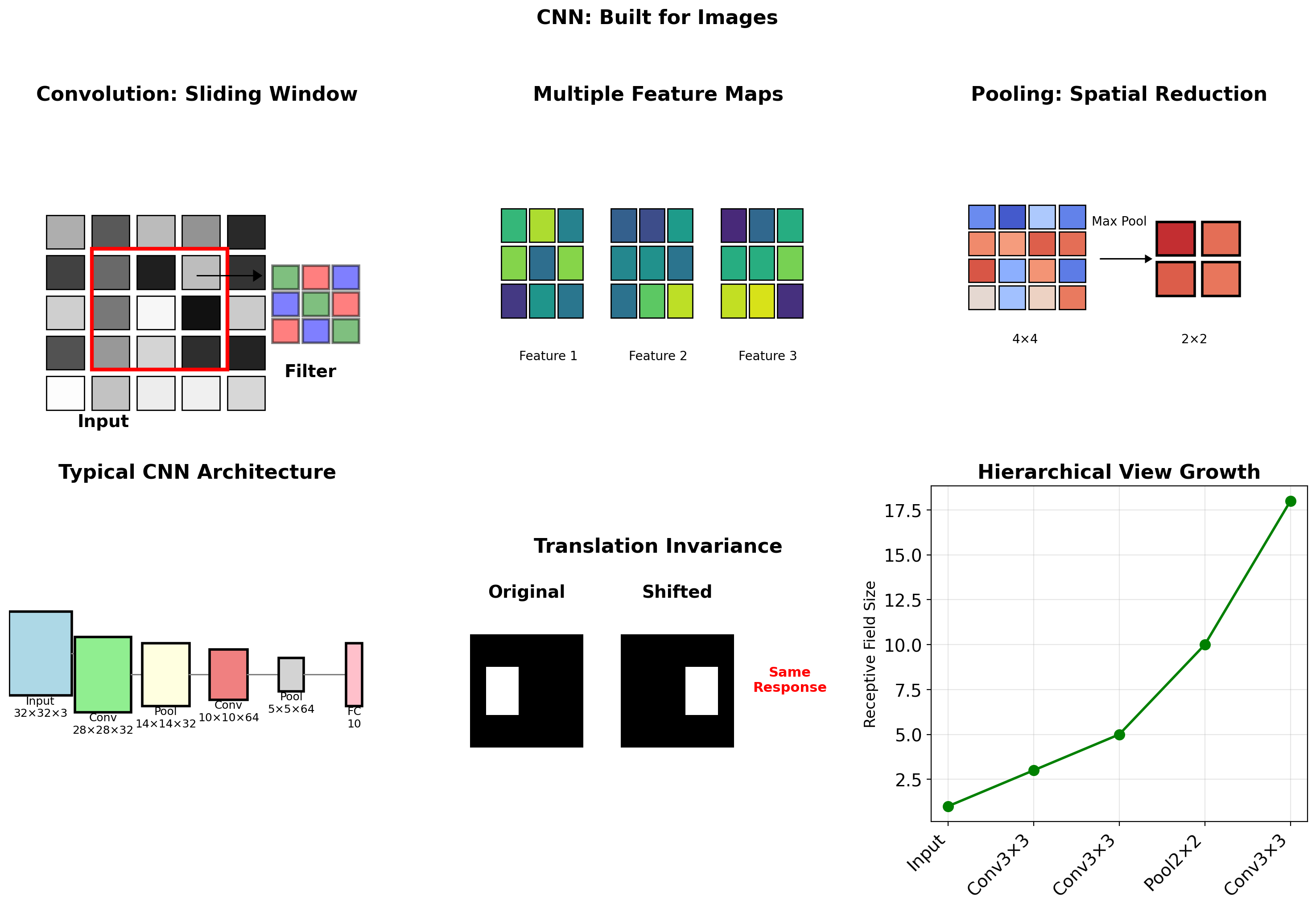
Convolutional Networks: Exploiting Spatial Structure

CNNs exploit the spatial structure of images through local connectivity and weight sharing. This architecture receives detailed implementation.

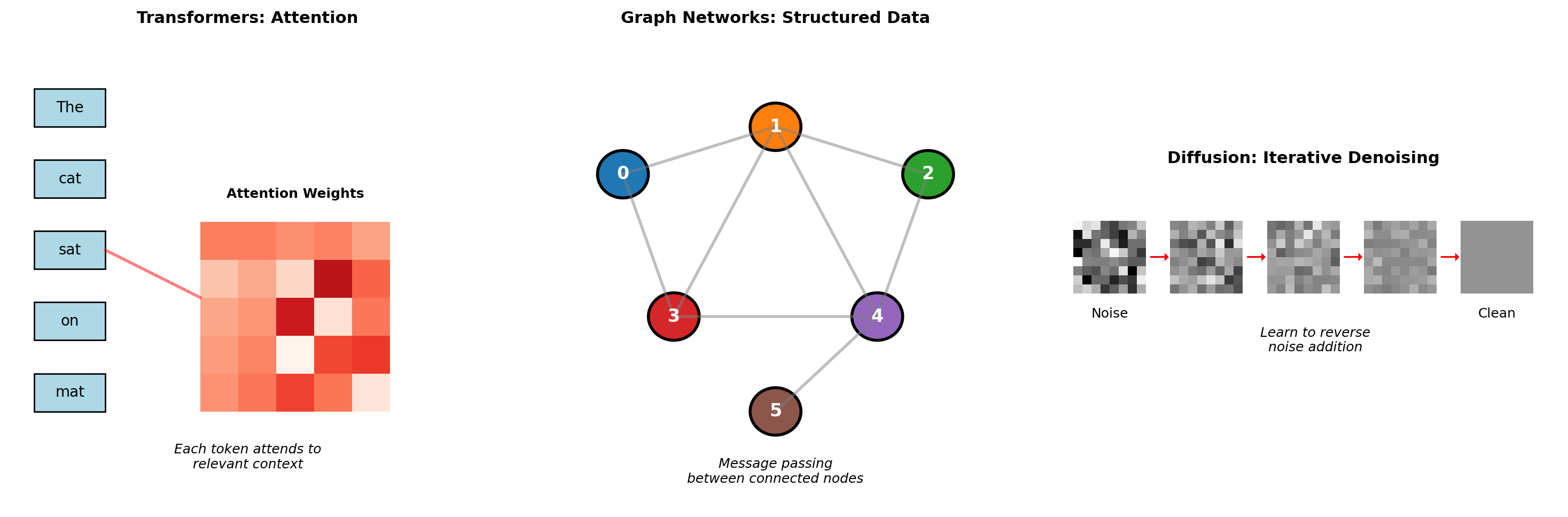
Preview: Transformers, Graph Networks, and Diffusion Models

Modern architectures go beyond CNNs, but the principles remain: exploit structure, learn efficiently, scale appropriately.

Building a Simple CNN

import numpy as np

class Conv2D:
    def __init__(self, in_channels, out_channels, kernel_size=3):
        self.in_channels = in_channels
        self.out_channels = out_channels
        self.kernel_size = kernel_size
        
        # Initialize filters
        self.filters = np.random.randn(
            out_channels, in_channels, kernel_size, kernel_size
        ) * 0.1
        self.bias = np.zeros(out_channels)
    
    def forward(self, x):
        batch, in_c, height, width = x.shape
        out_h = height - self.kernel_size + 1
        out_w = width - self.kernel_size + 1
        
        output = np.zeros((batch, self.out_channels, out_h, out_w))
        
        # Convolution operation
        for b in range(batch):
            for oc in range(self.out_channels):
                for h in range(out_h):
                    for w in range(out_w):
                        # Extract patch
                        patch = x[b, :, h:h+self.kernel_size, w:w+self.kernel_size]
                        # Convolve with filter
                        output[b, oc, h, w] = np.sum(patch * self.filters[oc]) + self.bias[oc]
        
        return output

class MaxPool2D:
    def __init__(self, pool_size=2):
        self.pool_size = pool_size
    
    def forward(self, x):
        batch, channels, height, width = x.shape
        out_h = height // self.pool_size
        out_w = width // self.pool_size
        
        output = np.zeros((batch, channels, out_h, out_w))
        
        for h in range(out_h):
            for w in range(out_w):
                h_start = h * self.pool_size
                w_start = w * self.pool_size
                pool_region = x[:, :, h_start:h_start+self.pool_size, 
                              w_start:w_start+self.pool_size]
                output[:, :, h, w] = np.max(pool_region, axis=(2, 3))
        
        return output

# Example usage
x = np.random.randn(1, 3, 32, 32)  # Batch=1, RGB, 32x32
conv = Conv2D(3, 16, kernel_size=3)
pool = MaxPool2D(pool_size=2)

x = conv.forward(x)
print(f"After conv: {x.shape}")  # (1, 16, 30, 30)
x = np.maximum(0, x)  # ReLU
x = pool.forward(x)
print(f"After pool: {x.shape}")  # (1, 16, 15, 15)

After conv: (1, 16, 30, 30)
After pool: (1, 16, 15, 15)

This simple implementation shows the core operations. In practice, PyTorch handles gradients automatically.

Architecture Efficiency on ImageNet

ResNet-50 (2015):

• 25M parameters
• 76% top-1 accuracy
• 10ms inference (GPU)

MobileNetV2 (2018):

• 3.5M parameters (7× smaller)
• 72% top-1 accuracy (4% drop)
• 3ms inference (3× faster)

EfficientNet-B0 (2019):

• 5M parameters (5× smaller than ResNet)
• 77% top-1 accuracy (1% higher than ResNet)
• 4ms inference (2.5× faster)

Architecture design matters: EfficientNet achieves better accuracy than ResNet-50 with far fewer parameters.

The Practice of Deep Learning

A Recipe for Training Neural Networks

The Training Loop

\[\theta_{t+1} = \theta_t - \eta \cdot \frac{1}{|B|} \sum_{i \in B} \nabla_\theta \mathcal{L}(f_\theta(x_i), y_i)\]

Karpathy’s Principles

1. Become one with the data Look at your data. Plot it. Understand its distribution, outliers, patterns.

2. Set up end-to-end pipeline Get a simple model training before complexity.

3. Overfit a single batch If you can’t overfit 10 examples, something is broken.

4. Verify loss at initialization Check loss matches expected value (e.g., \(\log(n_{classes})\) for classification).

5. Add complexity gradually Start simple, add one thing at a time.

# The debugging progression
def debug_training():
    # Step 1: Overfit one example
    single_x = X[0:1]
    single_y = y[0:1]
    for _ in range(100):
        loss = train_step(single_x, single_y)
    assert loss < 0.01, "Can't overfit single"
    
    # Step 2: Overfit small batch  
    batch_x = X[0:10]
    batch_y = y[0:10]
    for _ in range(500):
        loss = train_step(batch_x, batch_y)
    assert loss < 0.1, "Can't overfit batch"
    
    # Step 3: Check with real data
    # Only now move to full dataset
    return "Ready for full training"

Karpathy’s recipe emphasizes systematic debugging. Most failures come from rushing to complexity too quickly.

Debugging Deep Learning

Most deep learning debugging follows common patterns. Systematic approaches save time over random hyperparameter tuning.

Medical Imaging: High Accuracy Hides Dataset Problems

Setup:

• Train pneumonia detector on chest X-rays
• Dataset: 10,000 images from Hospital A
• Training accuracy: 95%
• Validation accuracy: 94%
• Model looks ready to deploy

Deployment at Hospital B:

• Accuracy drops to 72%
• False negatives increase 3×

What went wrong:

Hospital A used one X-ray machine model with specific image characteristics. Hospital B used different equipment. Model learned machine artifacts, not disease patterns.

Example artifacts learned:

• Brightness/contrast settings
• Image resolution differences
• Metal markers in specific corners
• Patient positioning conventions

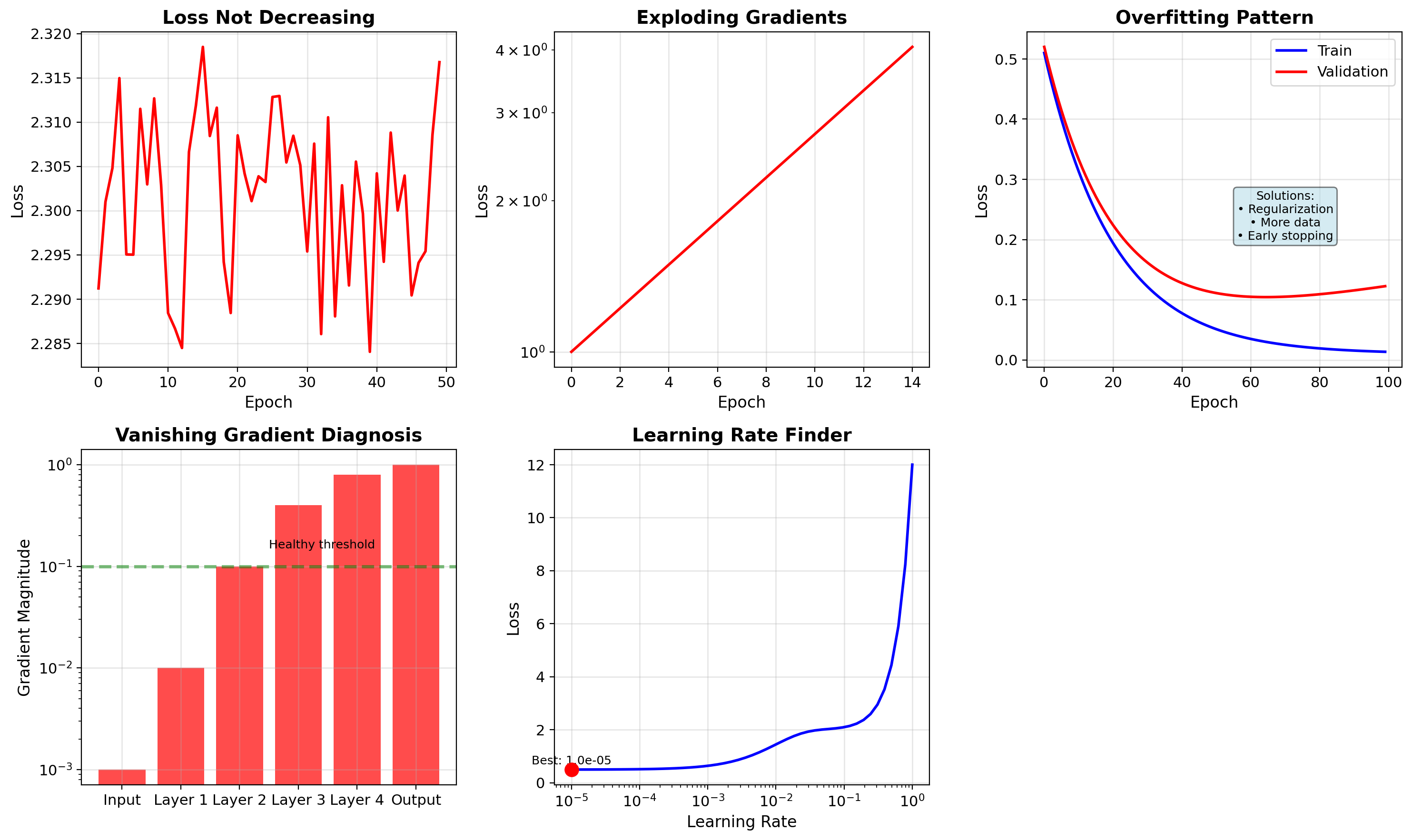
Shortcut learning: Standard debugging looked fine:

• Training loss decreasing smoothly
• No overfitting (train/val gap small)
• High validation accuracy
• Good precision/recall on test set

Problem only appeared on different hospital equipment. Models exploit spurious correlations (disease + specific machine) as shortcuts instead of learning actual medical patterns.

Computational Realities

Hardware acceleration is essential for deep learning. Understanding computational constraints helps in designing experiments.

What this means for this course:

CPU (your laptop):

• Sufficient for: Most course assignments including smaller CNNs
• Time scale: Minutes per epoch on MNIST, tens of minutes on CIFAR-10
• Cost: Free

GPU (Colab/Kaggle free tier):

• Useful for: Faster iteration, larger architectures, final project
• Time scale: Seconds per epoch
• Cost: Free (with session limits)

Multi-GPU (cloud):

• Rarely needed: Only for very large-scale experiments
• Cost: $1-3 per hour

Course approach: CPU is viable for most work. GPU accelerates but isn’t required.

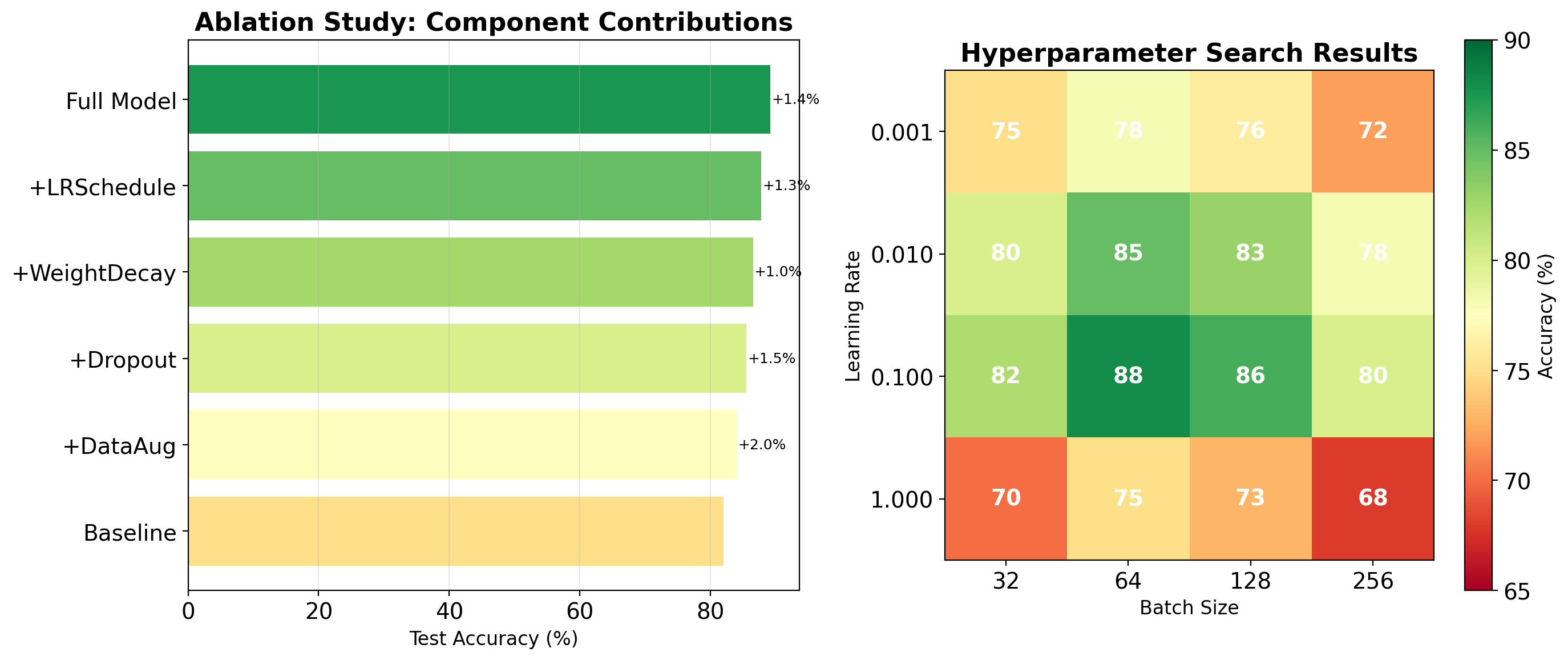
Systematic Experimentation

# Tracking experiments
experiment_config = {
    'model': 'resnet18',
    'dataset': 'cifar10',
    'batch_size': 128,
    'lr': 0.1,
    'epochs': 100,
    'seed': 42,
    'timestamp': '2025-01-15-14:30'
}

# Always set seeds for reproducibility
def set_all_seeds(seed=42):
    np.random.seed(seed)
    # torch.manual_seed(seed)
    # torch.cuda.manual_seed_all(seed)
    # random.seed(seed)
    
# Log everything
def log_metrics(epoch, train_loss, val_loss, val_acc):
    metrics = {
        'epoch': epoch,
        'train_loss': train_loss,
        'val_loss': val_loss,
        'val_acc': val_acc,
        'lr': get_current_lr(),
        'timestamp': time.time()
    }
    # Write to file, tensorboard, wandb, etc.
    return metrics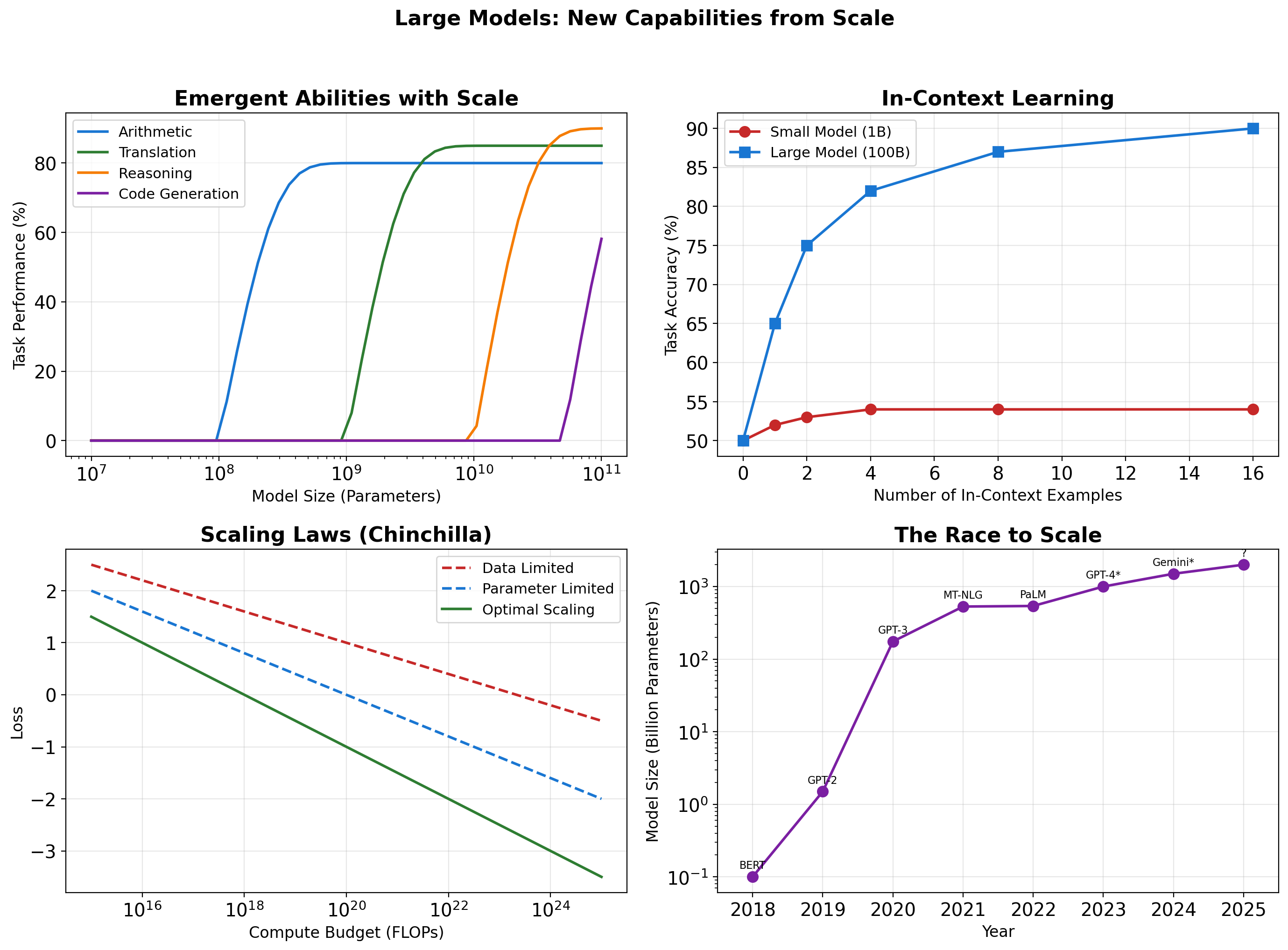

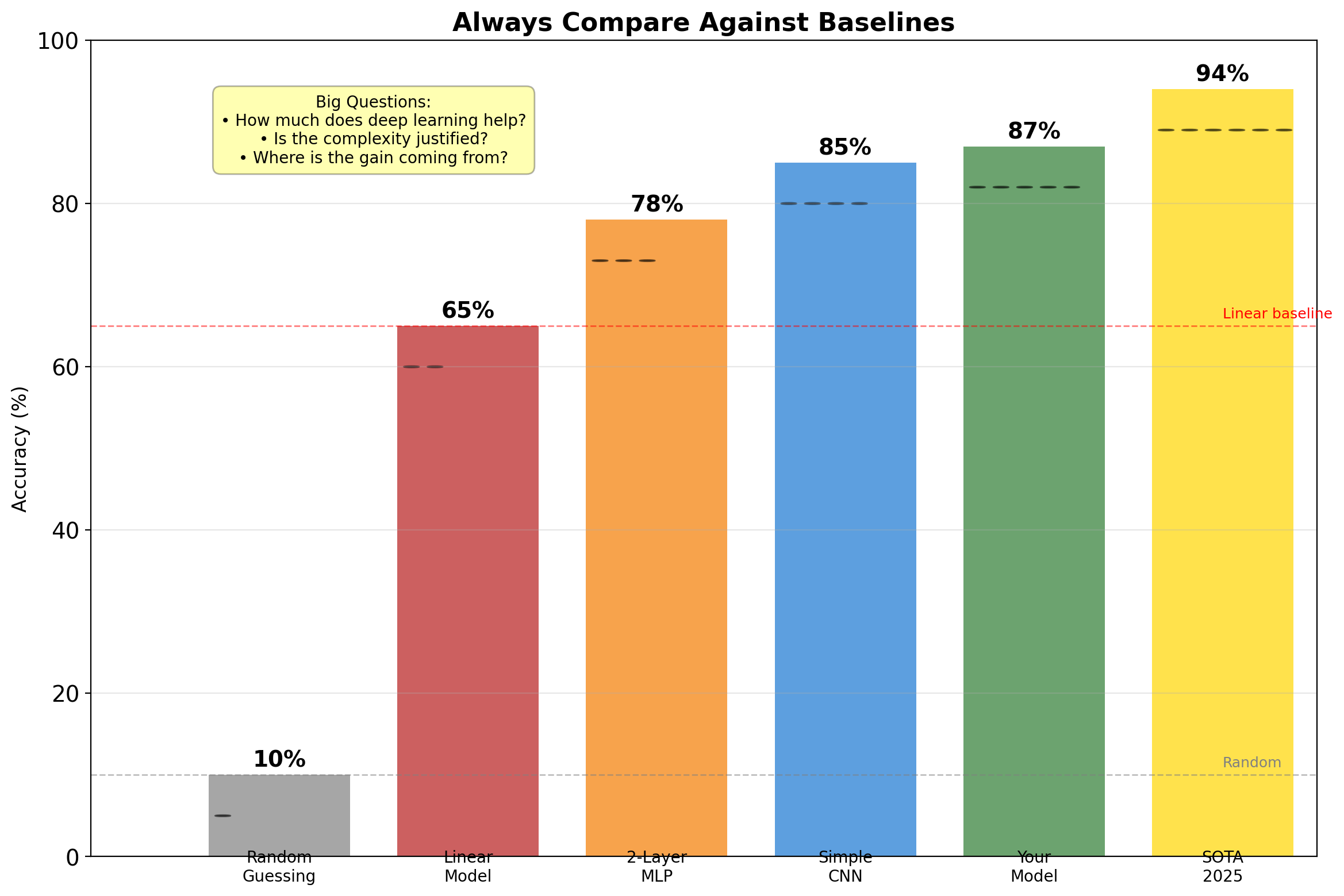
Systematic experimentation with proper tracking and ablations reveals what determines performance.

Always Establish Baselines Before Claiming Improvement

Always establish baselines. A 2% improvement over a strong baseline is more impressive than 90% accuracy in isolation.

Current Frontiers & Course Roadmap

Course Architecture: Statistical to Neural

This course uniquely bridges classical statistical methods with modern deep learning, giving you foundations most pure DL courses skip.

Scaling Laws and Emergent Capabilities

Scale has revealed surprising emergent abilities. Models suddenly acquire capabilities that smaller versions completely lack.

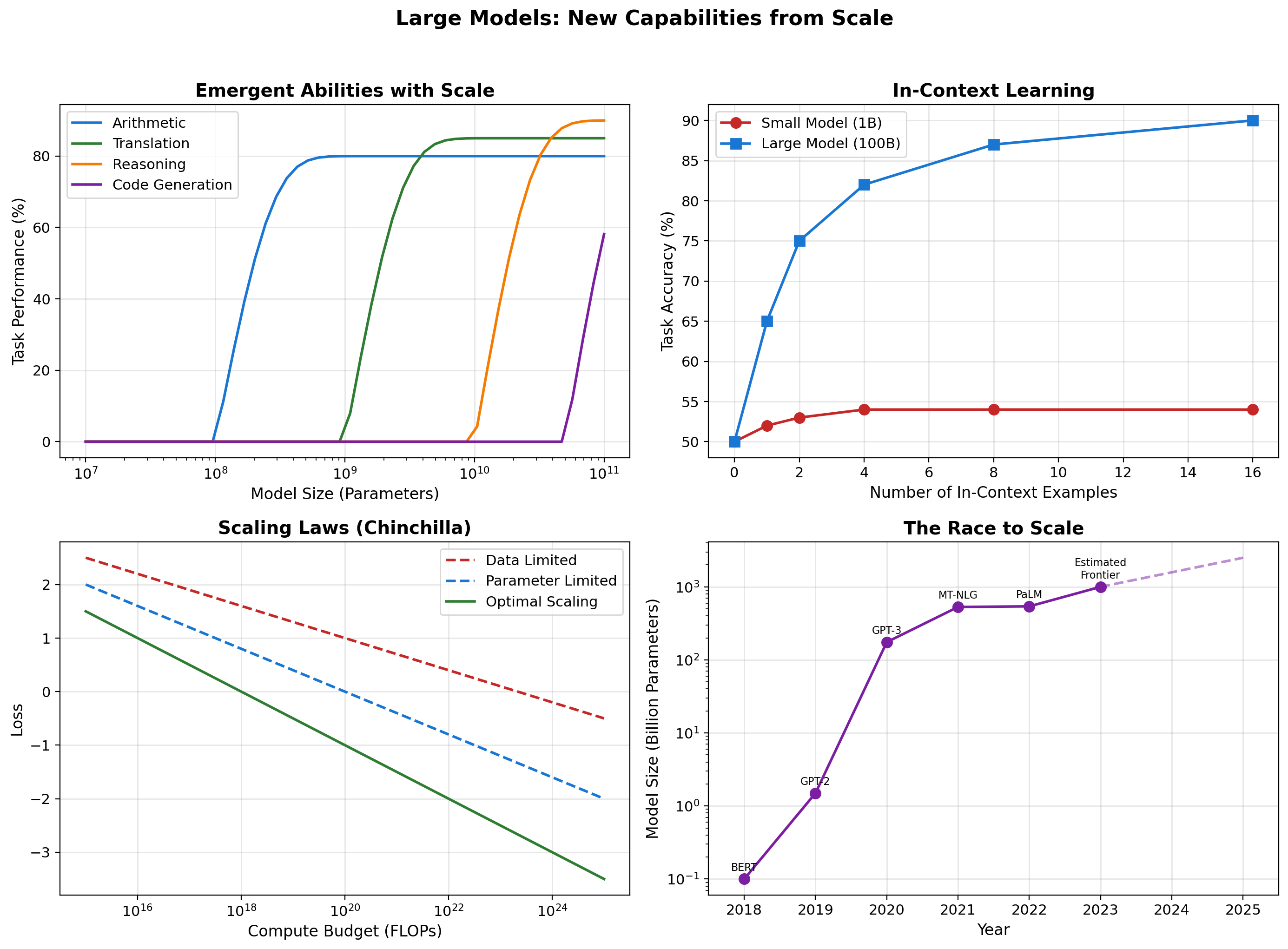
What these scales cost:

GPT-2 (1.5B params, 2019):

• Training: ~$50K compute, weeks on multi-GPU
• Inference: Runs on laptop CPU

GPT-3 (175B params, 2020):

• Training: ~$5M compute, months on cluster
• Inference: Requires GPU server

PaLM (540B params, 2022):

• Training: ~$10M+ compute, specialized infrastructure
• Inference: Multi-GPU required

Scale is not just about bigger numbers - it’s about fundamentally different resource requirements.

Model Compression and Acceleration

Efficiency research makes deep learning practical. The goal is maintaining performance while reducing computational costs.

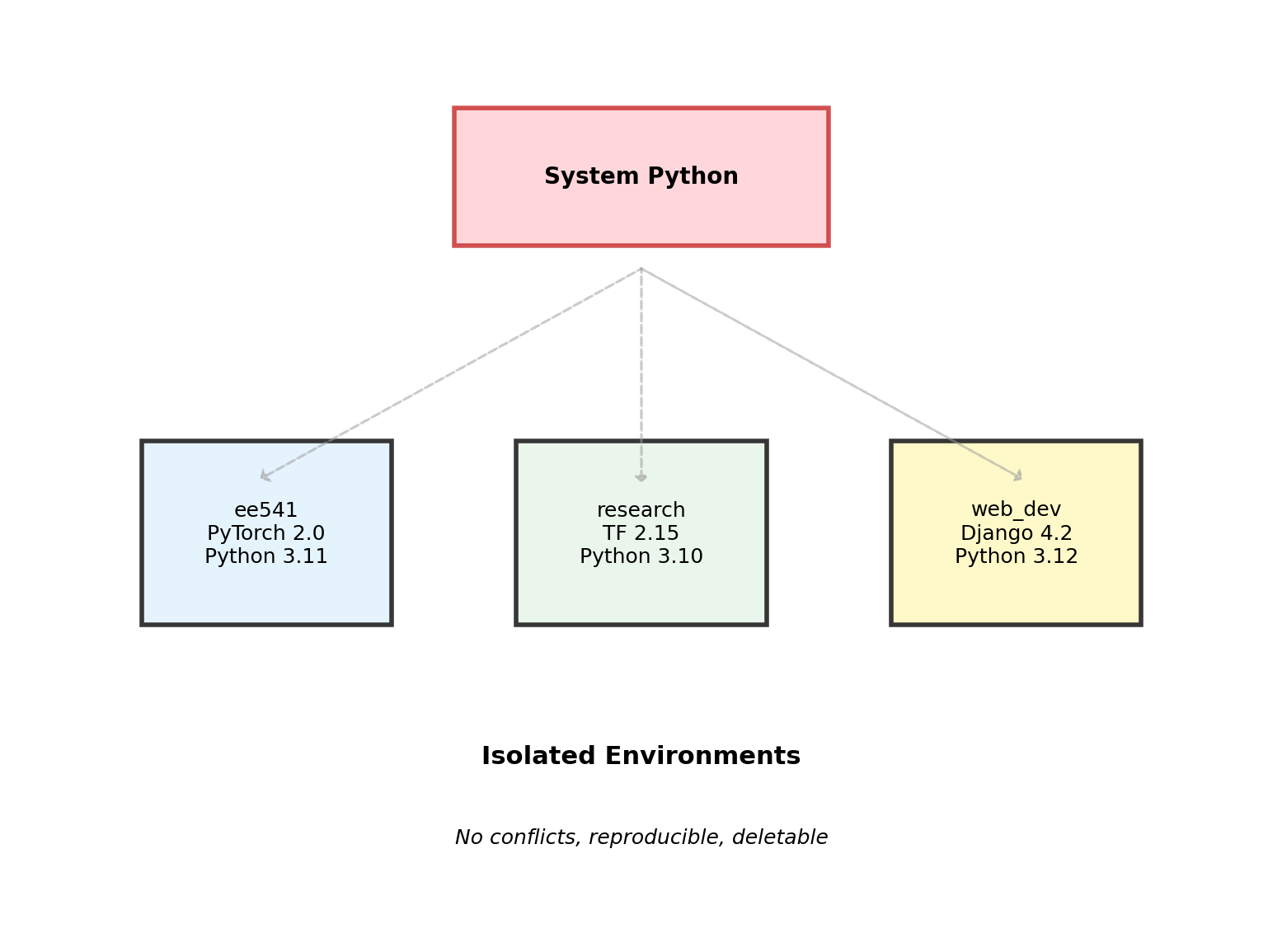
Python Environment Setup

Environment Management: Why It Matters

Dependency Conflicts

# System Python - Don't do this
python install torch
# Error: requires numpy>=1.19
pip install numpy==1.20
# Breaks: opencv requires numpy==1.18

Conflicts are inevitable. Each project needs:

• Specific Python version
• Specific package versions
• Isolated from system Python

Virtual Environments

Virtual environments are essential for reproducible research. Each project gets its own isolated Python installation.

Conda: Package and Environment Management

Installation

# Download Miniconda (minimal) or Anaconda (full)
# miniconda.anaconda.com

# After installation, verify:
conda --version
conda info

# Update conda itself
conda update -n base conda

Create Course Environment

# Create environment with Python 3.11
conda create -n ee541 python=3.11

# Activate environment
conda activate ee541

# Your prompt changes:
(ee541) $ 

# Deactivate when done
conda deactivate

Why Conda for Deep Learning

Binary package management

• Precompiled CUDA libraries
• Optimized BLAS/LAPACK
• No compilation required

Cross-platform

• Same commands on Windows/Mac/Linux
• Handles system dependencies

Channel system

• conda-forge: Community packages
• pytorch: Official PyTorch builds
• nvidia: CUDA toolkit

Environment files

• Share exact environment
• environment.yml for reproducibility

Conda handles both Python packages and system libraries, crucial for deep learning frameworks that depend on CUDA.

Essential Package Installation

# Activate your environment first
conda activate ee541

# Core scientific stack
conda install numpy scipy matplotlib pandas

# Jupyter for notebooks
conda install jupyter ipykernel

# Register kernel for Jupyter
python -m ipykernel install --user --name ee541 --display-name "Python (ee541)"

# PyTorch - SELECT BASED ON YOUR SYSTEM
# CPU only
conda install pytorch torchvision torchaudio cpuonly -c pytorch

# CUDA 11.8 (NVIDIA GPU)
conda install pytorch torchvision torchaudio pytorch-cuda=11.8 -c pytorch -c nvidia

# Mac M1/M2/M3 (Metal Performance Shaders)
conda install pytorch torchvision torchaudio -c pytorch

# Additional ML tools
conda install scikit-learn
conda install -c conda-forge tensorboard

GPU Configuration Check

• NVIDIA: Check CUDA version with nvidia-smi
• AMD: ROCm support limited, use CPU fallback
• Mac (MPS): Automatic detection in PyTorch 1.12+

# Standard device selection
import torch

if torch.cuda.is_available():
    device = torch.device("cuda")
elif torch.backends.mps.is_available():
    device = torch.device("mps")
else:
    device = torch.device("cpu")

print(f"Using device: {device}")

PyTorch installation varies by system. The course will primarily use CPU for initial weeks, GPU for CNNs.

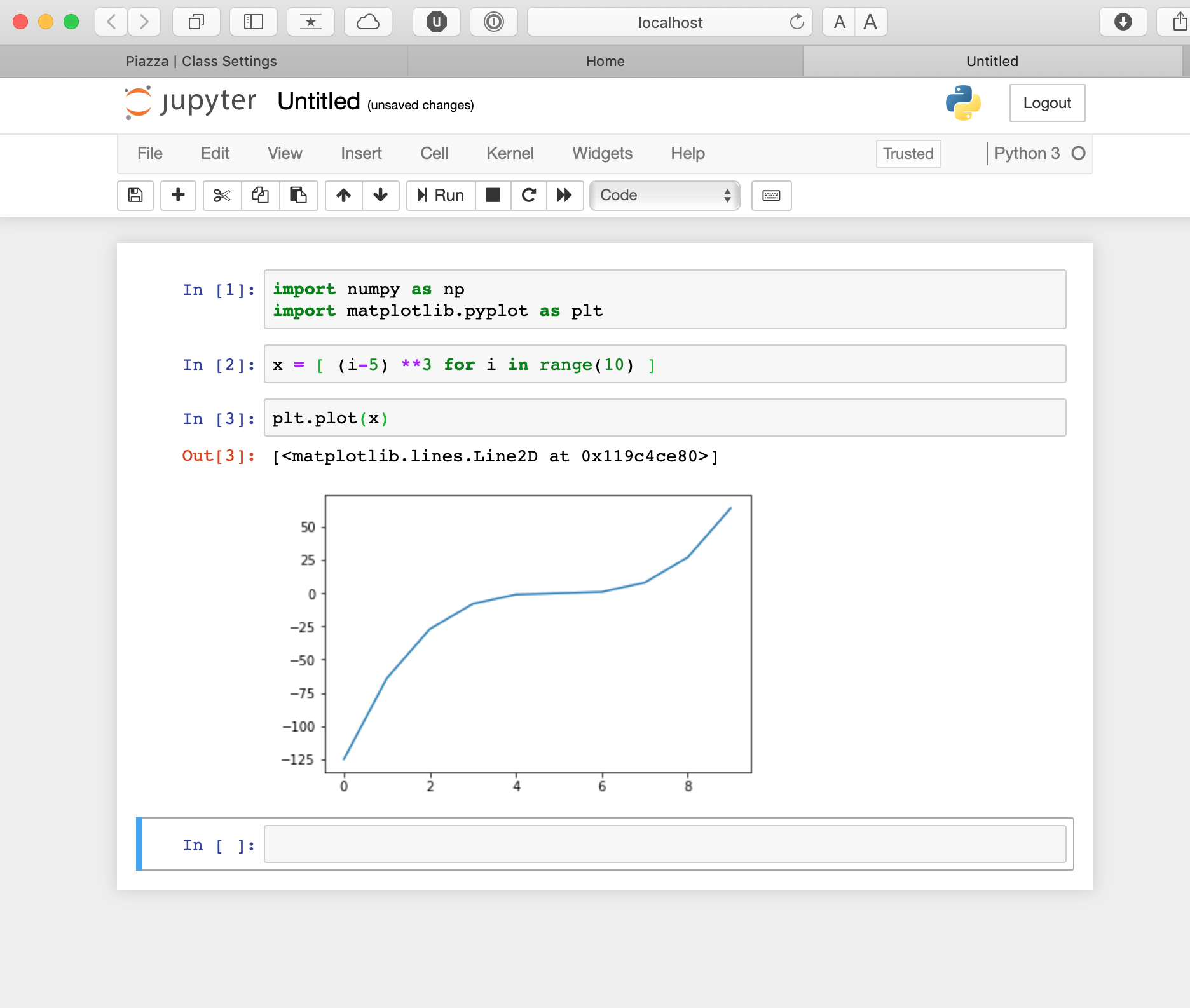
Jupyter Notebooks: Interactive Development

Starting Jupyter

# From terminal with environment active
(ee541) $ jupyter notebook

# Opens browser at localhost:8888
# Navigate to your work directory

Notebook Structure

• Cells: Code or Markdown
• Kernel: Python process executing code
• State: Variables persist between cells

Key Shortcuts

• Shift+Enter: Run cell, move to next
• Ctrl+Enter: Run cell, stay
• Esc: Command mode
• Enter: Edit mode
• A/B: Insert cell above/below

Jupyter Notebook Interface

Notebooks are ideal for experimentation and learning. We’ll use them for homework but scripts for final projects.

Real-World Example: Trading Algorithm

Jupyter Project Example

This shows a real project combining data loading, analysis, and algorithm implementation - the same workflow used in research and industry.

Project Management

Version Control

git init
git add .
git commit -m "Initial commit"

# But exclude:
# .gitignore contents:
*.pyc
__pycache__/
.ipynb_checkpoints/
data/
*.pt
*.pth

Reproducibility

# Save environment
conda env export > environment.yml

# Recreate elsewhere
conda env create -f environment.yml

# Save pip requirements
pip freeze > requirements.txt

Good organization from the start saves time later. Keep data separate from code, use version control for code only.

Verifying Your Environment

import sys
import platform

print(f"Python: {sys.version}")
print(f"Platform: {platform.platform()}")

packages = {
    'numpy': None,
    'torch': None,
    'torchvision': None,
    'matplotlib': None,
    'jupyter': None,
    'sklearn': 'scikit-learn'
}

for import_name, pip_name in packages.items():
    try:
        module = __import__(import_name)
        version = getattr(module, '__version__', 'installed')
        print(f"✓ {import_name}: {version}")
        
        # Special check for PyTorch GPU
        if import_name == 'torch':
            import torch
            if torch.cuda.is_available():
                print(f"  GPU: CUDA ({torch.version.cuda})")
                print(f"  Device: {torch.cuda.get_device_name(0)}")
            elif torch.backends.mps.is_available():
                print(f"  GPU: MPS (Mac)")
            else:
                print(f"  GPU: Not available")
                
    except ImportError:
        package = pip_name or import_name
        print(f"✗ {import_name}: Not installed")
        print(f"  Install with: conda install {package}")

Python: 3.11.8 | packaged by conda-forge | (main, Feb 16 2024, 20:49:36) [Clang 16.0.6 ]
Platform: macOS-26.2-arm64-arm-64bit
✓ numpy: 1.26.4
✓ torch: 2.5.1
  GPU: MPS (Mac)
✓ torchvision: 0.20.1
✓ matplotlib: 3.10.6
✓ jupyter: installed
✓ sklearn: 1.6.1

Environment Management Commands

Conda Essentials

# List environments
conda env list

# Create from file
conda env create -f environment.yml

# Clone environment
conda create --name ee541_backup --clone ee541

# Remove environment
conda env remove -n ee541

# Update all packages
conda update --all

# Clean cache (free space)
conda clean --all

Package Management

# Search for package
conda search pytorch

# Install specific version
conda install pytorch=2.0.1

# List installed packages
conda list

# Check for updates
conda update --dry-run --all

# Channel priority
conda config --add channels conda-forge
conda config --set channel_priority strict

These commands cover 90% of required operations. Keep this slide as a reference.

PyTorch Demo

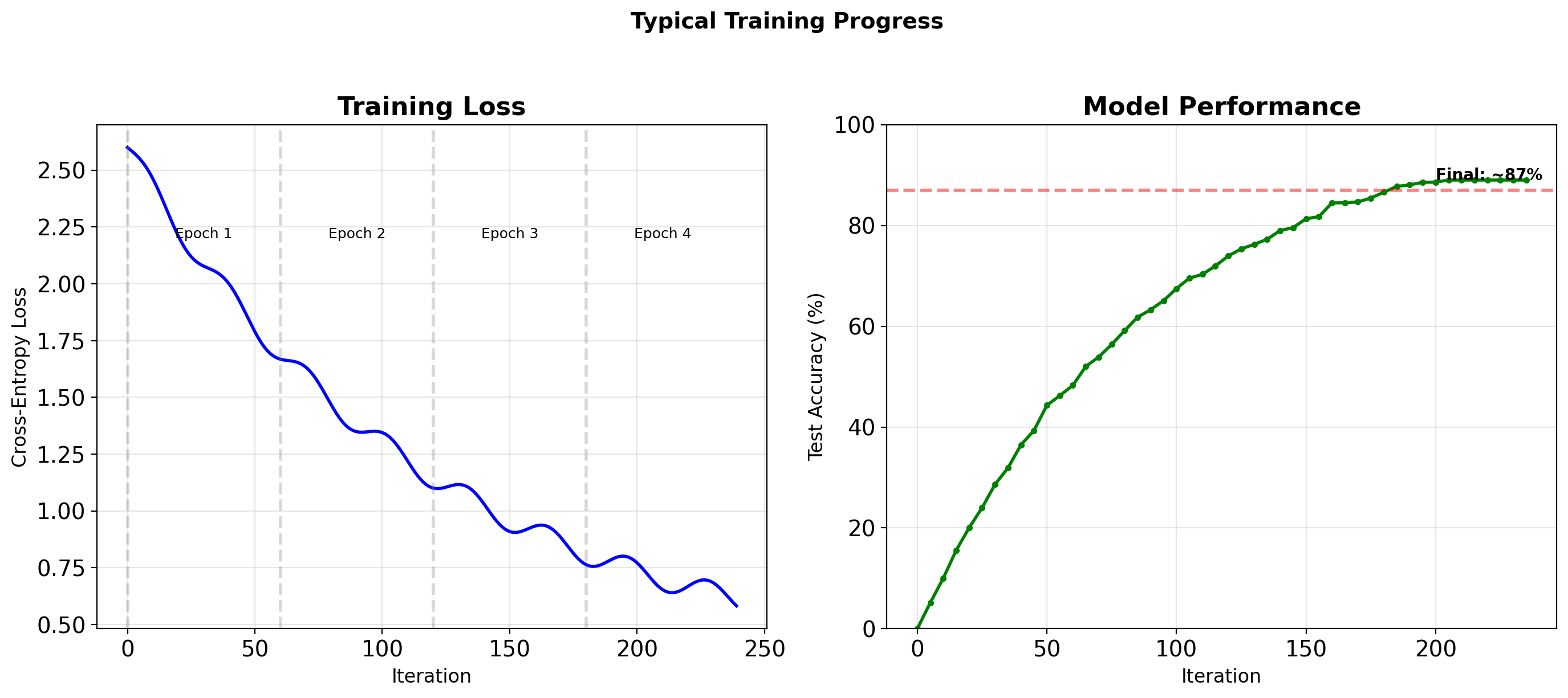
Fashion-MNIST: 87% Accuracy in Four Epochs

What We’re Building

Task: Classify clothing items into 10 categories

Architecture: Simple 2-layer network

• Input: 28×28 grayscale images (784 pixels)
• Hidden: 128 neurons with ReLU
• Output: 10 classes (softmax)

Training: 4 epochs, Adam optimizer

Files:

• 1-fashion-mnist.ipynb: Dataset exploration
• 2-minimal-pytorch.ipynb: Core training loop
• 3-feature-visualization.ipynb: TensorBoard monitoring

T-shirt

Trouser

Pullover

Dress

Coat

Sandal

Shirt

Sneaker

Bag

Boot

Fashion-MNIST is harder than digits - real clothing items with texture and shape variation. Good first test of neural networks.

Core Training Loop Structure

# Minimal.ipynb - Key components

# 1. Data Loading
train_loader = DataLoader(train_set, batch_size=100, shuffle=True)
test_loader = DataLoader(test_set, batch_size=100, shuffle=False)

# 2. Model Definition
class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.hidden = nn.Linear(784, 128)
        self.output = nn.Linear(128, 10)
    
    def forward(self, x):
        x = F.relu(self.hidden(x))
        return self.output(x)

# 3. Training Loop
for epoch in range(num_epochs):
    for images, labels in train_loader:
        # Forward pass
        outputs = model(images.view(-1, 784))
        loss = loss_func(outputs, labels)
        
        # Backward pass
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

Training Performance Benchmarks

Complete training in ~5 minutes on CPU, <1 minute on GPU

This is the standard PyTorch pattern used throughout the course. Notice the clear separation of data, model, and training.

Training Dynamics

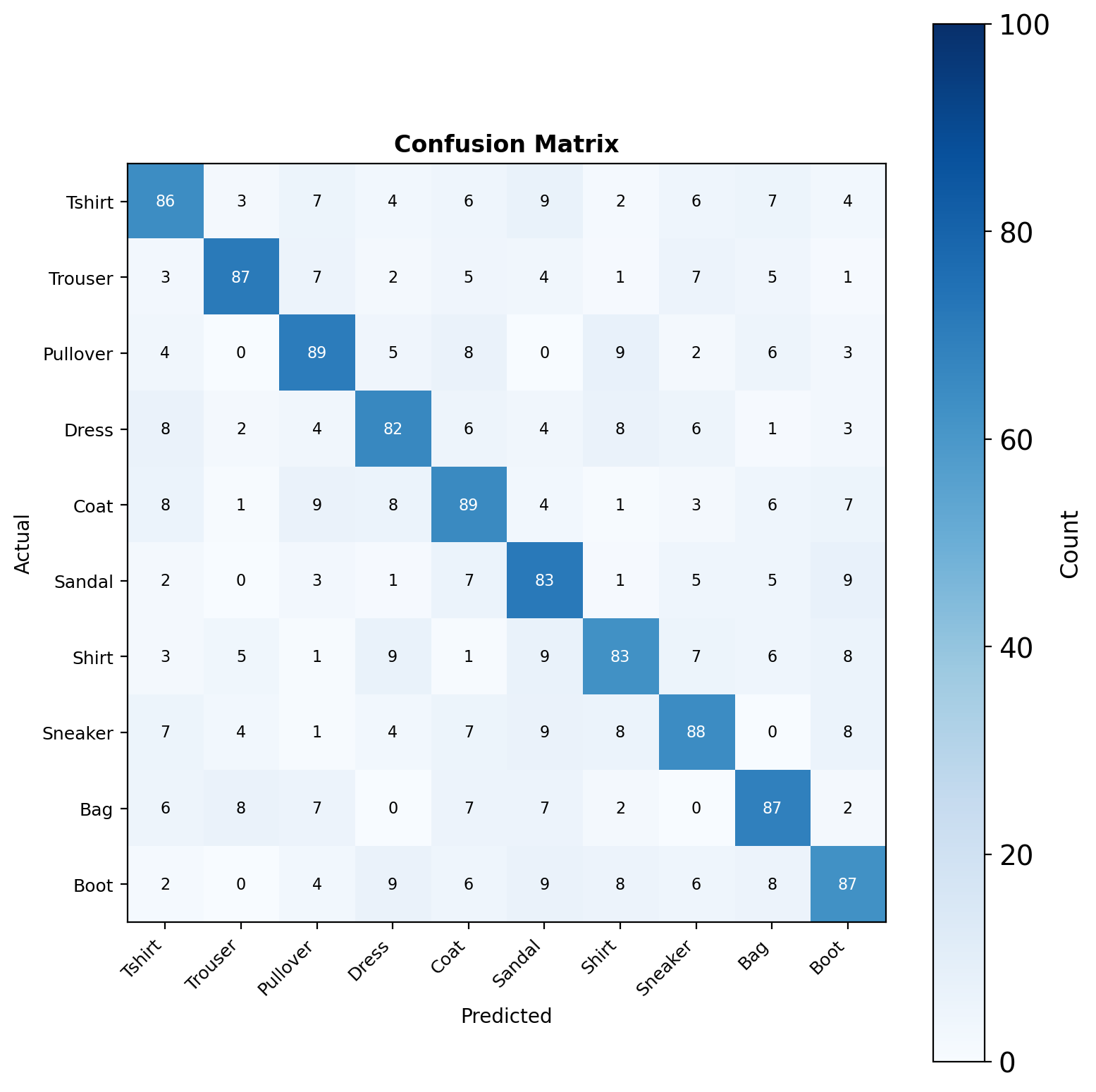
Observations:

• Rapid initial learning (first epoch)
• Diminishing returns with more training
• Test accuracy plateaus around 87% for this simple model

Notice the characteristic learning curve - fast initial progress then slower refinement. This pattern appears across all neural network training.

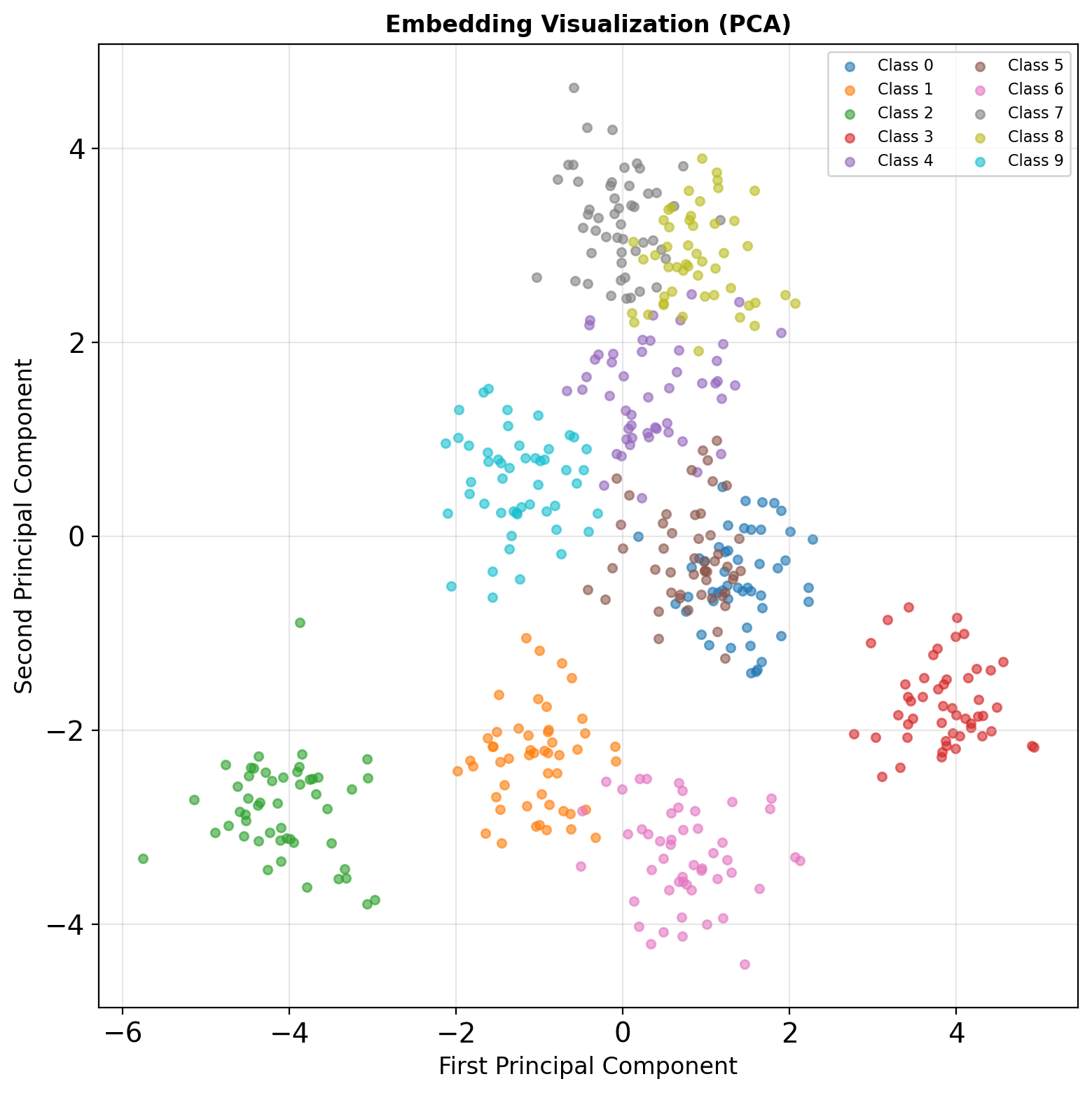
TensorBoard Visualization

Launch TensorBoard

# From terminal
tensorboard --logdir runs
# Navigate to http://localhost:6006

Available Visualizations

• Scalars: Loss, accuracy over time
• Images: Sample predictions
• Graph: Network architecture
• Embeddings: Feature space (PCA/t-SNE)
• Histograms: Weight distributions

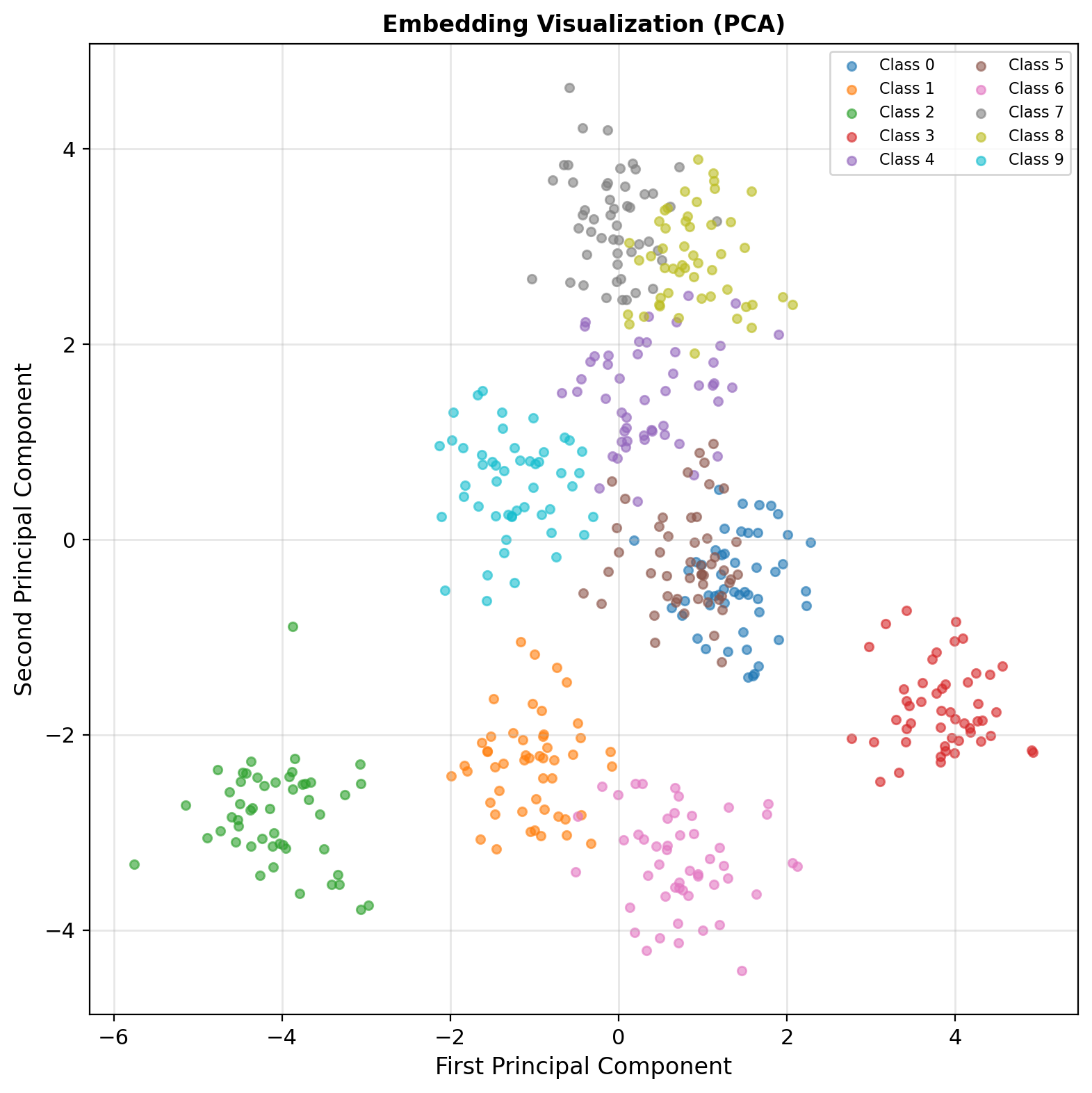
Embedding Insight: Classes form distinct clusters in feature space

TensorBoard provides real-time monitoring. The embedding visualization shows that the network learns to separate classes in feature space.

Model Architecture Inspection

A simple 2-layer network has over 100K parameters. Most are in the first layer connecting all pixels to hidden units.

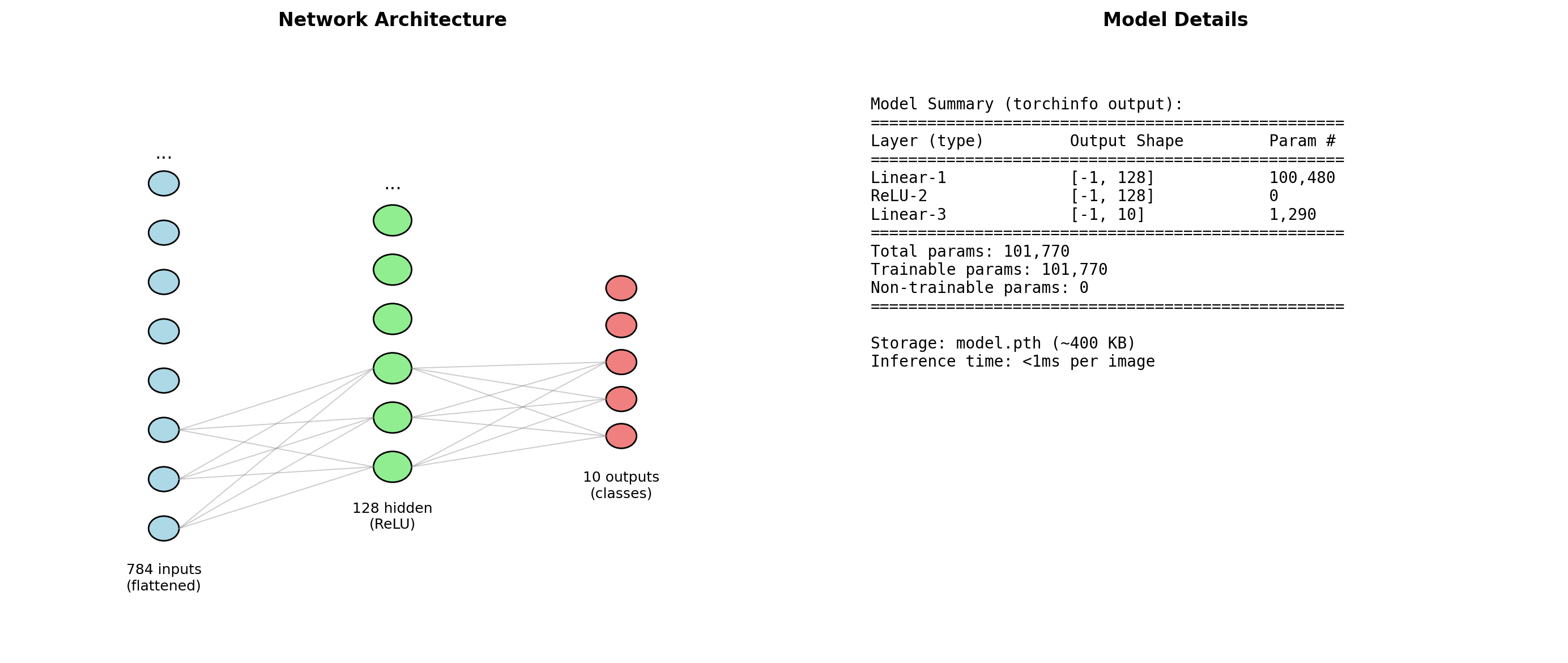
87% Accuracy Achieved with Simple Architecture

Implementation Results

• Model: 2-layer MLP with 128 hidden units
• Performance: 87% test accuracy after 4 epochs
• Training time: ~2 minutes on CPU
• Bottom line: Simple architectures work well for Fashion-MNIST

Not Addressed (Future Topics)

• Overfitting analysis: No train/val split comparison
• Hyperparameter tuning: Fixed learning rate, no grid search
• Architecture search: Only tried one configuration
• Regularization: No dropout, weight decay, or data augmentation
• Optimizer exploration: Only tried Adam, not SGD variants or AdamW

Main Files

1-fashion-mnist.ipynb      # Dataset exploration
2-minimal-pytorch.ipynb    # Core training
3-feature-visualization.ipynb  # TensorBoard

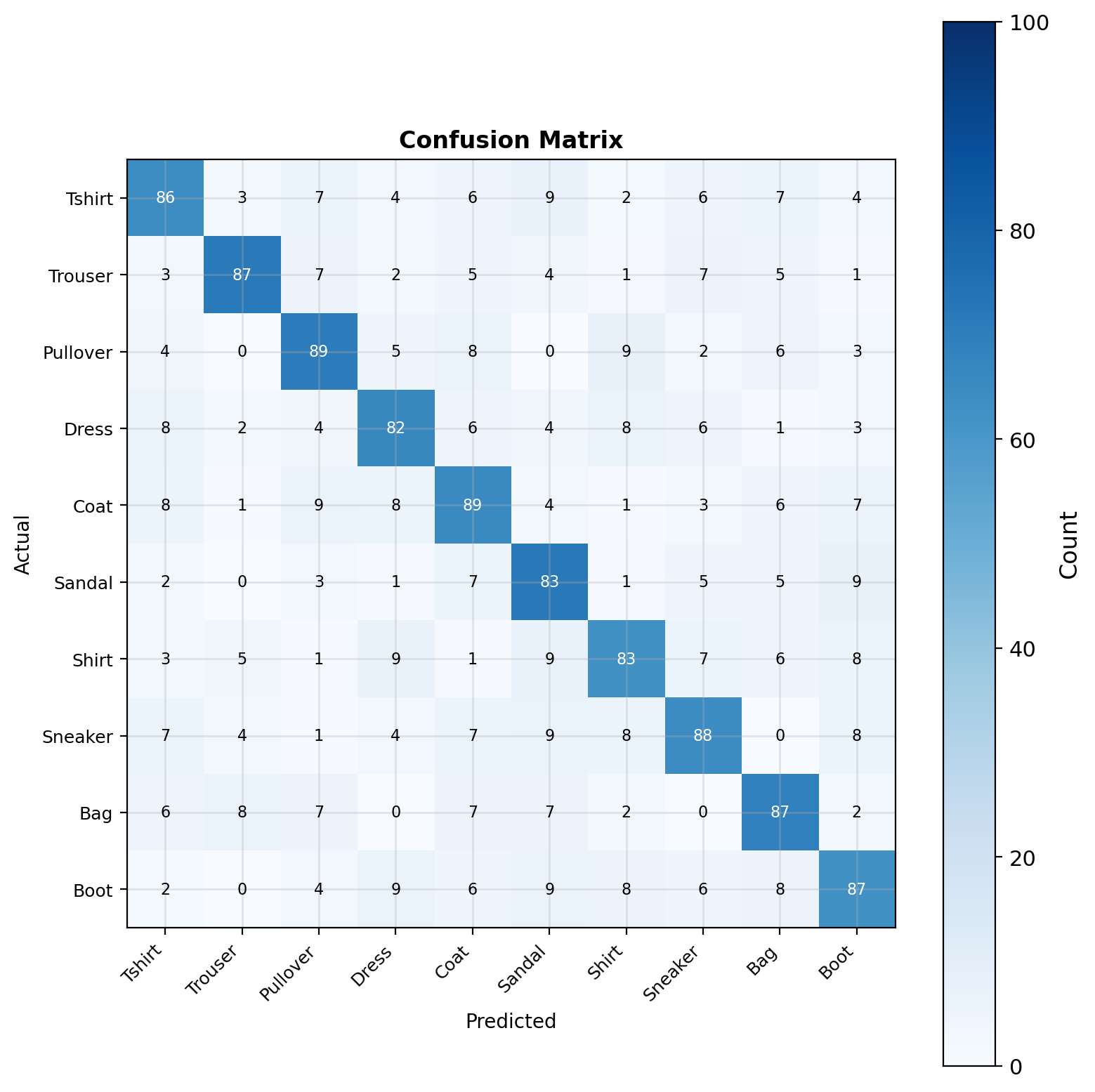
Common Confusions: Shirt ↔︎ T-shirt, Pullover ↔︎ Coat

Python and NumPy for Neural Networks

Next week: Array operations and automatic differentiation

This simple example contains all the elements of modern deep learning. We’ll build on this foundation throughout the course.