Python Fundamentals
EE 541 - Unit 2
Spring 2026
Outline
Python Internals
- Everything is an object with type and refcount
- Variables as labels, not containers
- Dynamic typing costs
- List over-allocation, dict hash tables
- Mutable defaults trap
- First-class functions, LEGB scope
- Closures and captured state
- Operator overloading via dunder methods
Scientific Computing
- Why Python is slow; how NumPy fixes it
- Contiguous memory, vectorization
- Broadcasting, views vs copies
- Generator architecture and reproducibility
- Monte Carlo integration
- BLAS/LAPACK wrappers, sparse matrices
- Matplotlib object hierarchy
Why Python?
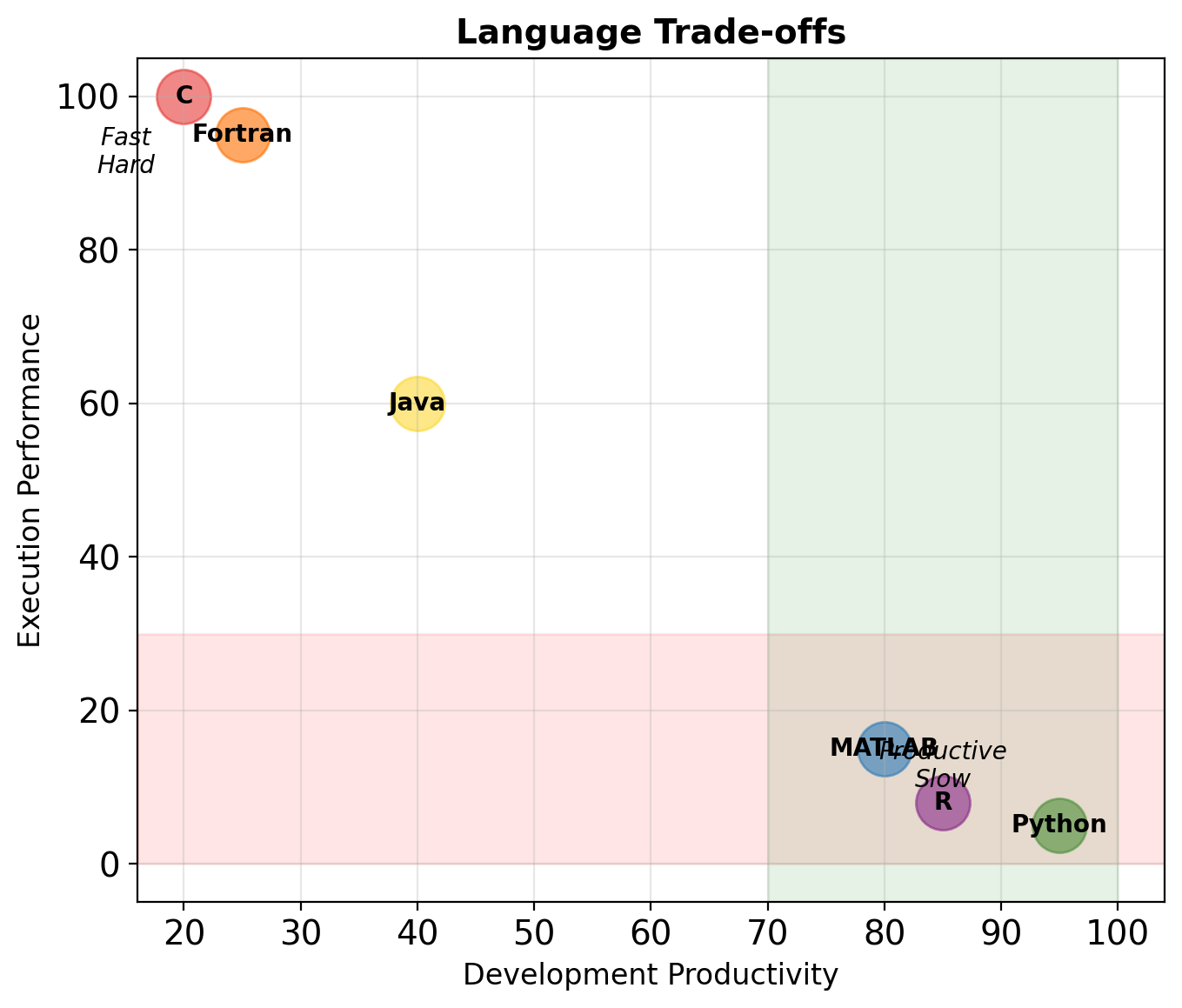
Why Python for Scientific Computing?
A Paradox
Python is 10-100× slower than C/C++ for raw computation, yet dominates scientific computing. Why?
Design Philosophy
- Readability over performance: Code is read more than written
- Dynamic over static: Flexibility for exploration
- Extensive standard library: Reduces external dependencies
- Glue language: Binds fast libraries (NumPy, SciPy use C/Fortran)
The Two-Language Problem
Traditional approach: prototype in MATLAB/Python, rewrite in C++ for production
Python’s approach: Python for control flow, C for computation
Python’s Object Model
Everything in Python is an object:
Every Object Contains:
- Reference count: How many variables point to it
- Type pointer: What kind of object it is
- Value/Data: The actual content
- Additional metadata: Size, flags, etc.
Consequences:
- Integer
5takes 28 bytes (vs 4 in C) - Every operation involves indirection
- Type checking happens at runtime
- Memory scattered across heap
This overhead is why NumPy exists — it stores raw C arrays with a thin Python wrapper.
import sys
# Simple integer
x = 42
print(f"Integer 42:")
print(f" Size: {sys.getsizeof(x)} bytes")
print(f" ID: {id(x):#x}")
print(f" Type: {type(x)}")
# List of integers
lst = [1, 2, 3, 4, 5]
print(f"\nList [1,2,3,4,5]:")
print(f" List object: {sys.getsizeof(lst)} bytes")
print(f" Plus 5 integers: {5 * sys.getsizeof(1)} bytes")
print(f" Total: ~{sys.getsizeof(lst) + 5*28} bytes")
# C equivalent would be 20 bytes (5 × 4)Integer 42:
Size: 28 bytes
ID: 0x1046734d0
Type: <class 'int'>
List [1,2,3,4,5]:
List object: 104 bytes
Plus 5 integers: 140 bytes
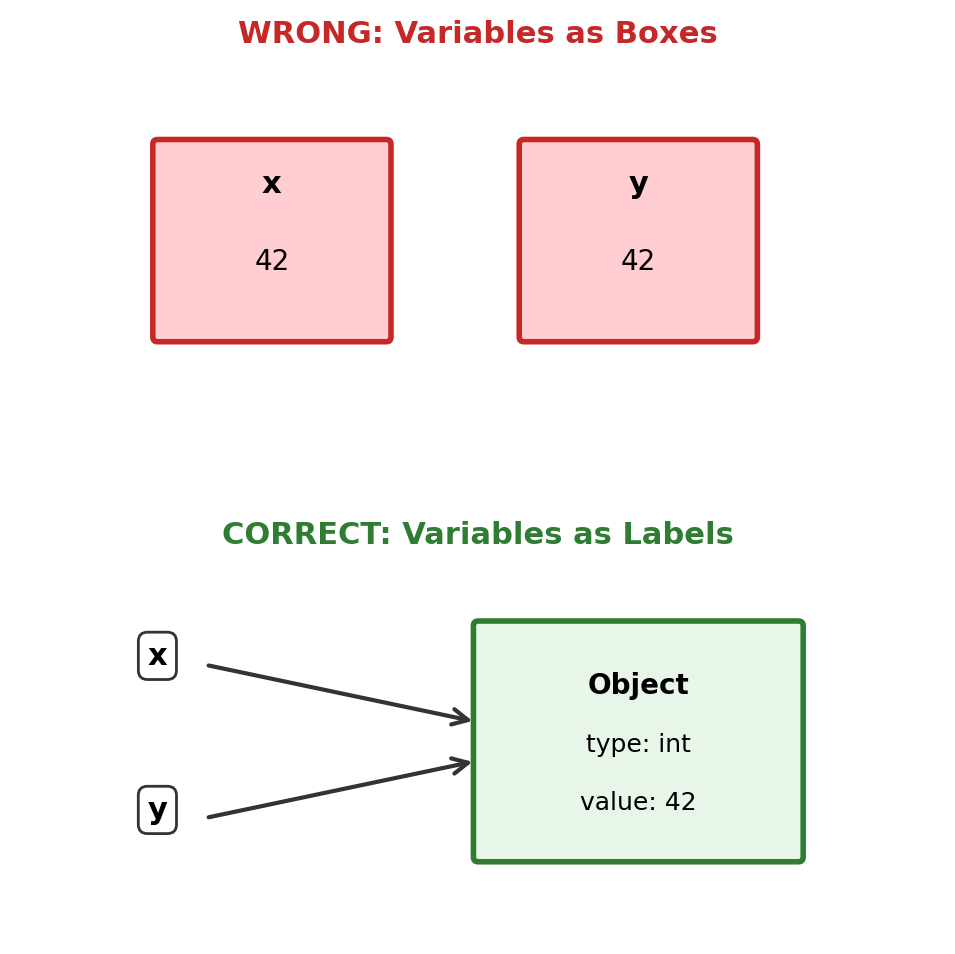
Total: ~244 bytesVariables Are Not Boxes
Variables are names bound to objects, not storage locations.
x = [1, 2, 3] # x refers to a list object
y = x # y refers to THE SAME object
y.append(4) # Modifying through y
print(f"x = {x}") # x sees the change!
# To create a copy:
z = x.copy() # or x[:] or list(x)
z.append(5)
print(f"x = {x}, z = {z}") # x unchangedx = [1, 2, 3, 4]
x = [1, 2, 3, 4], z = [1, 2, 3, 4, 5]Assignment creates a reference, not a copy.
Dynamic Typing: Cost and Benefit
Python determines types at runtime, not compile time.
Static Typing (C/Java)
Compiler knows:
- Exact memory layout
- Which CPU instruction to use
- No runtime checks needed
Dynamic Typing (Python)
Runtime must:
- Look up type of
a - Look up type of
b
- Find correct
__add__method - Handle type mismatches
- Create new object for result
Performance Impact
import timeit
import operator
# Python function call overhead
def python_add(a, b):
return a + b
# Direct operator
op_add = operator.add
a, b = 5, 10
n = 1000000
t1 = timeit.timeit(lambda: a + b, number=n)
t2 = timeit.timeit(lambda: op_add(a, b), number=n)
t3 = timeit.timeit(lambda: python_add(a, b), number=n)
print(f"Direct +: {t1:.3f}s")
print(f"operator.add: {t2:.3f}s ({t2/t1:.1f}x slower)")
print(f"Function: {t3:.3f}s ({t3/t1:.1f}x slower)")Direct +: 0.019s
operator.add: 0.024s (1.3x slower)
Function: 0.033s (1.7x slower)Control Flow: Iterator Protocol
Every for loop in Python uses the iterator protocol, not index-based access.
What Really Happens
Translates to:
iterator = iter(sequence)
while True:
try:
item = next(iterator)
process(item)
except StopIteration:
breakThis Enables:
- Lazy evaluation (generators)
- Infinite sequences
- Custom iteration behavior
- Memory efficiency
# Create a custom iterator
class Fibonacci:
def __init__(self, max_n):
self.max_n = max_n
self.n = 0
self.current = 0
self.next_val = 1
def __iter__(self):
return self
def __next__(self):
if self.n >= self.max_n:
raise StopIteration
result = self.current
self.current, self.next_val = \
self.next_val, self.current + self.next_val
self.n += 1
return result
# Use like any sequence
for f in Fibonacci(10):
print(f, end=' ')
print()
# This is why range() is memory efficient
print(f"\nrange(1000000): {sys.getsizeof(range(1000000))} bytes")0 1 1 2 3 5 8 13 21 34
range(1000000): 48 bytesFunctions: More Than Subroutines
Python functions are objects with attributes, not just code blocks.
Functions Are Objects
- Have attributes (
__name__,__doc__) - Can be assigned to variables
- Can be passed as arguments
- Can be returned from functions
- Carry their environment (closures)
This Enables:
- Functional programming patterns
- Decorators for cross-cutting concerns
- Callbacks and event handlers
- Factory functions
Key insight: Functions remember their creation environment.
def make_multiplier(n):
"""Factory function creating closures."""
def multiplier(x):
return x * n # n is captured
# Function is an object we can modify
multiplier.factor = n
multiplier.__name__ = f'times_{n}'
return multiplier
times_2 = make_multiplier(2)
times_10 = make_multiplier(10)
print(f"{times_2.__name__}: {times_2(5)}")
print(f"{times_10.__name__}: {times_10(5)}")
print(f"Factors: {times_2.factor}, {times_10.factor}")
# Inspect closure
import inspect
closure_vars = inspect.getclosurevars(times_2)
print(f"Captured: {closure_vars.nonlocals}")times_2: 10
times_10: 50
Factors: 2, 10
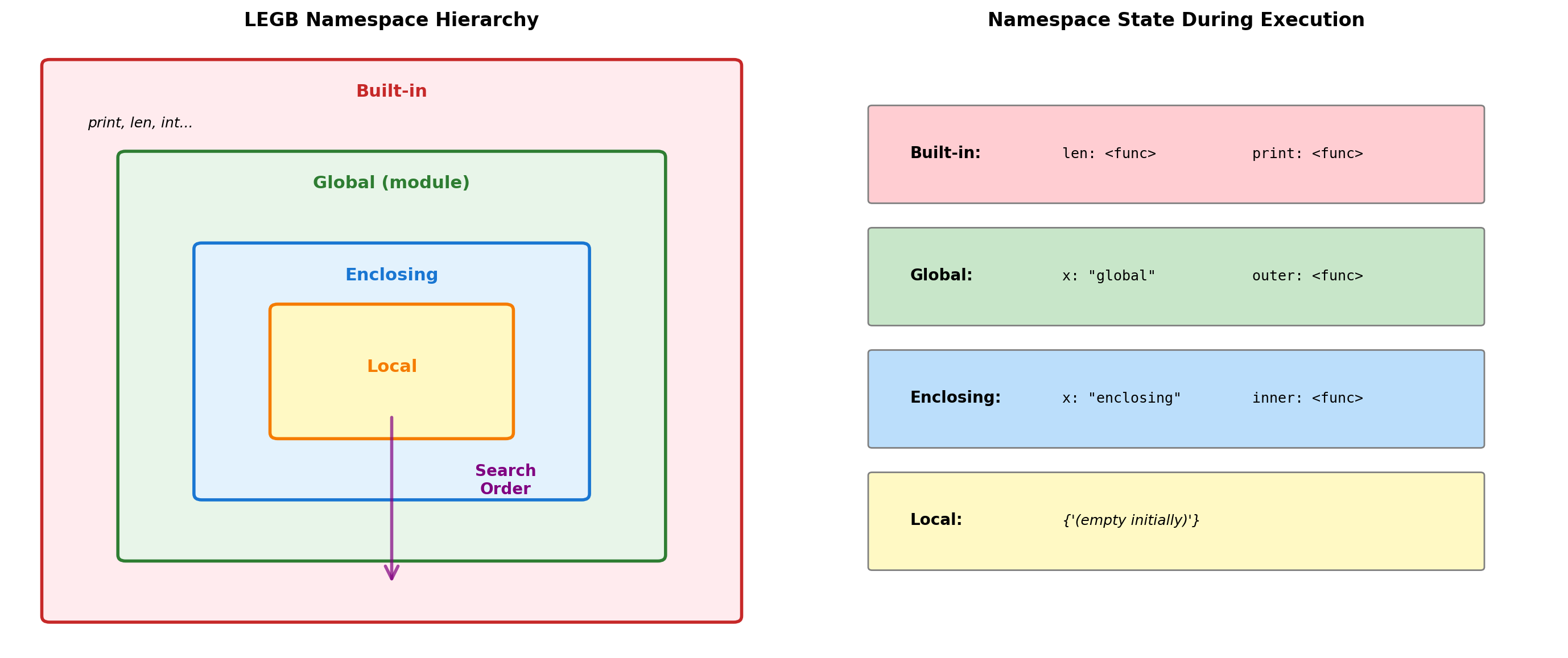
Captured: {'n': 2}Namespace Resolution: The LEGB Rule
Python resolves names through a hierarchy of namespace dictionaries.
x = "global" # Global namespace
def outer():
x = "enclosing" # Enclosing namespace
def inner():
print(f"Reading x: {x}") # LEGB search finds enclosing
def inner_local():
x = "local" # Creates local binding
print(f"Local x: {x}")
inner()
inner_local()
print(f"Enclosing x: {x}")
outer()
print(f"Global x: {x}")
# Namespace modification
def show_namespace_dict():
local_var = 42
print(f"locals(): {locals()}")
print(f"'local_var' in locals(): {'local_var' in locals()}")
show_namespace_dict()Reading x: enclosing
Local x: local
Enclosing x: enclosing
Global x: global
locals(): {'local_var': 42}
'local_var' in locals(): TrueResolution Rules:
- Local: Current function’s namespace
- Enclosing: Outer function(s) namespace
- Global: Module-level namespace
- Built-in: Pre-defined names
Binding Behavior:
- Assignment creates local binding by default
globalkeyword binds to global namespacenonlocalbinds to enclosing namespace- Reading doesn’t create binding
# UnboundLocalError example
count = 0
def increment():
# Python sees assignment, creates local slot
# But referenced before assignment
try:
count += 1 # UnboundLocalError
except UnboundLocalError as e:
print(f"Error: {e}")
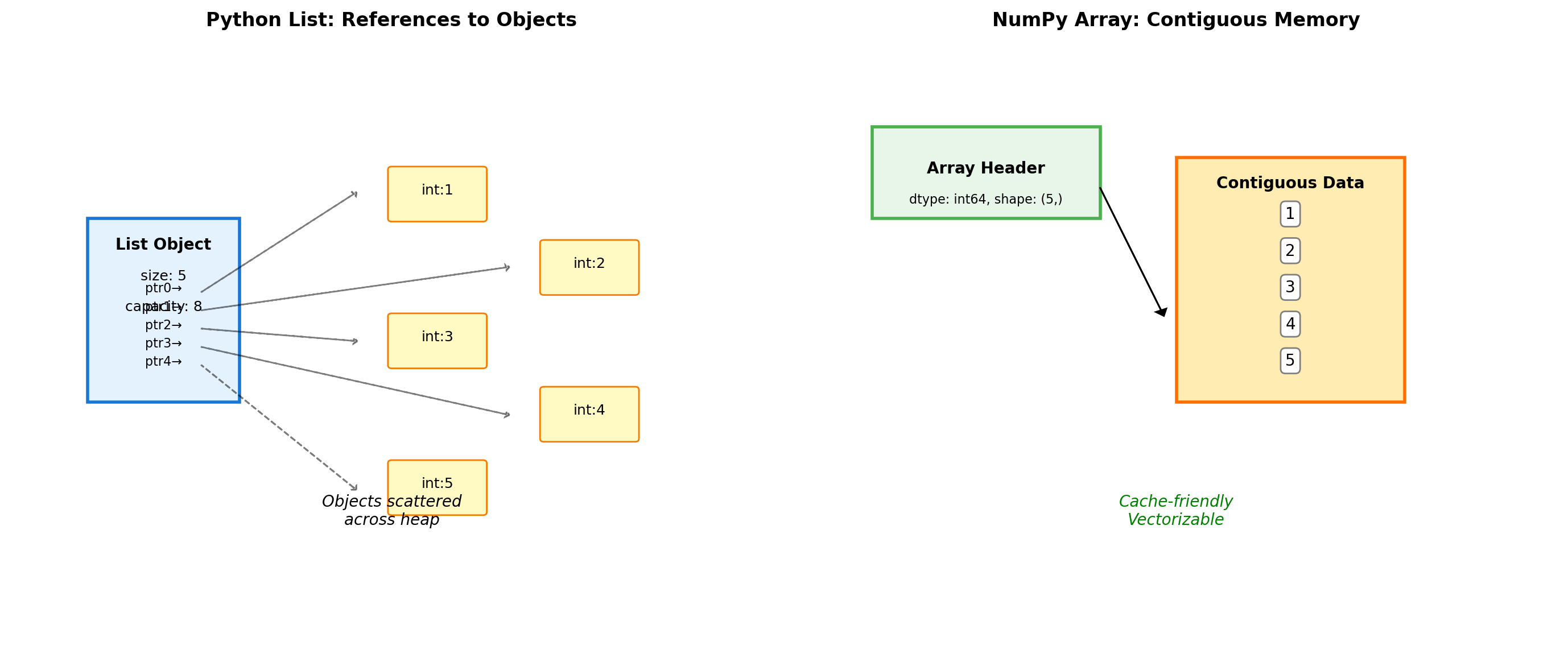
increment()Error: cannot access local variable 'count' where it is not associated with a valueLists vs Arrays: Memory Layout Matters
Python lists and NumPy arrays have different memory layouts.
import numpy as np
# Memory comparison
py_list = [1, 2, 3, 4, 5]
np_array = np.array([1, 2, 3, 4, 5])
print(f"Python list overhead: {sys.getsizeof(py_list)} bytes")
print(f"NumPy array overhead: {sys.getsizeof(np_array)} bytes")
print(f"NumPy data buffer: {np_array.nbytes} bytes")
# Performance impact
import timeit
lst = list(range(1000))
arr = np.arange(1000)
t_list = timeit.timeit(lambda: sum(lst), number=10000)
t_numpy = timeit.timeit(lambda: arr.sum(), number=10000)
print(f"\nSum 1000 elements:")
print(f"Python list: {t_list:.4f}s")
print(f"NumPy array: {t_numpy:.4f}s ({t_list/t_numpy:.1f}x faster)")Python list overhead: 104 bytes
NumPy array overhead: 152 bytes
NumPy data buffer: 40 bytes
Sum 1000 elements:
Python list: 0.0299s
NumPy array: 0.0073s (4.1x faster)Mutable vs Immutable: Design Consequences
Python’s distinction between mutable and immutable types affects program design.
Immutable Types
- int, float, str, tuple
- Cannot be changed after creation
- Safe to use as dict keys
- Thread-safe by default
- Can be cached/interned
Mutable Types
- list, dict, set, most objects
- Can be modified in place
- Cannot be dict keys
- Require synchronization
- Lead to aliasing bugs
# Immutable: operations create new objects
s = "hello"
print(f"Original id: {id(s):#x}")
s = s + " world" # Creates new object
print(f"After +=: {id(s):#x}")
# Mutable: operations modify in place
lst = [1, 2, 3]
original_id = id(lst)
lst.append(4) # Modifies in place
print(f"\nList id before: {original_id:#x}")
print(f"List id after: {id(lst):#x}")
print(f"Same object: {id(lst) == original_id}")
# The danger of mutable defaults
def add_to_list(item, target=[]): # Mutable default argument
target.append(item)
return target
list1 = add_to_list(1)
list2 = add_to_list(2) # Shares same default list
print(f"\nlist1: {list1}")
print(f"list2: {list2}")
print(f"Same object: {list1 is list2}")Original id: 0x110864cb0
After +=: 0x31f32ee30
List id before: 0x31f3d72c0
List id after: 0x31f3d72c0
Same object: True
list1: [1, 2]
list2: [1, 2]
Same object: TrueException Handling: Not Just Error Catching
Exceptions are Python’s control flow mechanism for exceptional cases.
Exceptions Are:
- Part of normal control flow
- Used by iterators (StopIteration)
- Hierarchical (inheritance-based catching)
- Expensive when raised, cheap when not
EAFP vs LBYL
- EAFP: Easier to Ask Forgiveness than Permission
- LBYL: Look Before You Leap
Python prefers EAFP:
import timeit
# EAFP vs LBYL performance
d = {str(i): i for i in range(100)}
def eafp_found():
try:
return d['50']
except KeyError:
return None
def lbyl_found():
if '50' in d:
return d['50']
return None
def eafp_not_found():
try:
return d['200']
except KeyError:
return None
def lbyl_not_found():
if '200' in d:
return d['200']
return None
n = 100000
print("Key exists:")
print(f" EAFP: {timeit.timeit(eafp_found, number=n):.3f}s")
print(f" LBYL: {timeit.timeit(lbyl_found, number=n):.3f}s")
print("Key missing:")
print(f" EAFP: {timeit.timeit(eafp_not_found, number=n):.3f}s")
print(f" LBYL: {timeit.timeit(lbyl_not_found, number=n):.3f}s")Key exists:
EAFP: 0.002s
LBYL: 0.004s
Key missing:
EAFP: 0.009s
LBYL: 0.002sPerformance: Optimization Strategies
Understanding Python’s overhead helps write efficient code.
Optimization Strategies:
- Vectorize with NumPy - Move loops to C
- Use built-in functions - Implemented in C
- Avoid function calls in loops - High overhead
- Cache method lookups -
append = lst.append - Use appropriate data structures - set for membership, deque for queues
# Example: Method lookup caching
data = []
n = 100000
# Slow: lookup append each time
start = timeit.default_timer()
for i in range(n):
data.append(i)
slow_time = timeit.default_timer() - start
# Fast: cache the method
data = []
append = data.append # Cache method lookup
start = timeit.default_timer()
for i in range(n):
append(i)
fast_time = timeit.default_timer() - start
print(f"Normal: {slow_time:.4f}s")
print(f"Cached: {fast_time:.4f}s ({slow_time/fast_time:.2f}x faster)")Normal: 0.0034s
Cached: 0.0039s (0.89x faster)Python Syntax Primer
What is Python?
Python is an interpreted, dynamically-typed, garbage-collected language.
Interpreted vs Compiled
| Compiled (C/C++) | Interpreted (Python) |
|---|---|
| Source → Machine code | Source → Bytecode → VM |
| Compile once, run fast | No compile step visible |
| Platform-specific binary | Platform-independent .pyc |
| Errors at compile time | Errors at runtime |
Python actually compiles to bytecode (.pyc files), then the Python Virtual Machine (PVM) interprets that bytecode. This is similar to Java’s JVM model.
Running Python Code
Three ways to run Python:
Interactive interpreter (REPL)
Script files
Jupyter notebooks
- Interactive cells mixing code, output, markdown
- Popular for exploration and visualization
The python command
When you type python script.py:
- Python reads
script.py(text file) - Lexer/parser converts to AST
- Compiler generates bytecode
- PVM executes bytecode line by line
Script structure:
Python’s Execution Model

Why this matters:
- No separate compile step — edit and run immediately
- Runtime errors only — syntax errors found when line executes
- Slower than native code — bytecode interpretation has overhead
- Dynamic features — can modify code at runtime (
eval,exec)
Comparison:
| C++ | Java | Python | |
|---|---|---|---|
| Compile to | Machine code | JVM bytecode | PVM bytecode |
| Type checking | Compile time | Compile time | Runtime |
| Speed | Fast | Medium | Slow |
| Edit-run cycle | Slow | Medium | Fast |
Variables and Types
Python variables are names bound to objects. No type declarations - the type belongs to the object, not the variable.
| Type | Example |
|---|---|
int |
42, -7 |
float |
3.14, 1e-5 |
str |
"hello" |
bool |
True, False |
None |
None |
Naming conventions:
snake_case- variables, functionsPascalCase- classesUPPER_CASE- constants
Multiple assignment and swap:
Strings and Formatting
Strings are immutable sequences of characters. f-strings (formatted string literals) are the modern way to build strings with embedded values.
Common format specifiers:
| Specifier | Output | Use case |
|---|---|---|
:.2f |
0.94 |
Fixed decimals |
:.2% |
94.23% |
Percentages |
:, |
1,000 |
Thousands separator |
:>10 |
hello |
Right-align, width 10 |
:.2e |
9.42e-01 |
Scientific notation |
Collections Overview
Python provides four core collection types, each with different performance characteristics:
| Type | Syntax | Mutable | Ordered | Duplicates |
|---|---|---|---|---|
| list | [1, 2, 3] |
Yes | Yes | Yes |
| tuple | (1, 2, 3) |
No | Yes | Yes |
| dict | {"a": 1} |
Yes | Yes* | Keys: No |
| set | {1, 2, 3} |
Yes | No | No |
*Dicts preserve insertion order (Python 3.7+)
Choosing the right collection:
- Need to modify elements? → list
- Fixed record (x, y, z)? → tuple
- Lookup by key? → dict
- Need unique values / fast membership? → set
Time complexity:
| Operation | list | dict | set |
|---|---|---|---|
Index x[i] |
O(1) | — | — |
Lookup x in |
O(n) | O(1) | O(1) |
| Append | O(1)* | — | O(1)* |
| Insert at i | O(n) | — | — |
| Delete | O(n) | O(1) | O(1) |
*Amortized — occasional resize is O(n)
Key insight: Use set or dict when you need fast in checks. Lists require scanning every element.
Lists: Mutable Sequences
Lists are ordered, mutable, and heterogeneous (can mix types).
layers = [64, 128, 256]
# Modify in place
layers.append(512) # Add to end
layers.insert(0, 32) # Insert at index
layers.extend([1024]) # Add multiple
print(f"After additions: {layers}")
# Remove elements
layers.pop() # Remove last
layers.remove(128) # Remove by value
print(f"After removals: {layers}")
# Sort and reverse
layers.sort() # In-place sort
print(f"Sorted: {layers}")
layers.reverse() # In-place reverse
print(f"Reversed: {layers}")After additions: [32, 64, 128, 256, 512, 1024]
After removals: [32, 64, 256, 512]
Sorted: [32, 64, 256, 512]
Reversed: [512, 256, 64, 32]List methods summary:
| Method | Effect | Returns |
|---|---|---|
append(x) |
Add to end | None |
extend(iter) |
Add all from iterable | None |
insert(i, x) |
Insert at index | None |
pop(i=-1) |
Remove at index | The element |
remove(x) |
Remove first occurrence | None |
sort() |
Sort in place | None |
reverse() |
Reverse in place | None |
copy() |
Shallow copy | New list |
index(x) |
Find index of x | int |
count(x) |
Count occurrences | int |
Note: Most methods modify the list in place and return None. Don’t write layers = layers.sort() — that sets layers to None.
Tuples: Immutable Sequences
Tuples are fixed-size, immutable sequences. Use them for records, multiple return values, and dict keys.
# Creating tuples
point = (3, 4)
rgb = (255, 128, 0)
single = (42,) # Note the comma!
empty = ()
# Unpacking
x, y = point
r, g, b = rgb
print(f"Point: x={x}, y={y}")
# Unpacking with * (rest)
first, *rest = [1, 2, 3, 4, 5]
print(f"First: {first}, Rest: {rest}")
# Swapping uses tuple packing/unpacking
a, b = 1, 2
a, b = b, a # Swap!
print(f"Swapped: a={a}, b={b}")Point: x=3, y=4
First: 1, Rest: [2, 3, 4, 5]
Swapped: a=2, b=1Why use tuples?
- Immutability as documentation — signals “don’t modify”
- Hashable — can be dict keys or set elements
- Slightly faster — no over-allocation overhead
- Multiple return values
def minmax(data):
"""Return (min, max) tuple."""
return min(data), max(data)
lo, hi = minmax([3, 1, 4, 1, 5, 9])
print(f"Range: {lo} to {hi}")
# Named tuples for clarity
from collections import namedtuple
Point = namedtuple('Point', ['x', 'y'])
p = Point(3, 4)
print(f"Point: {p.x}, {p.y}")
print(f"Distance: {(p.x**2 + p.y**2)**0.5:.2f}")Range: 1 to 9
Point: 3, 4
Distance: 5.00Dictionaries: Key-Value Mapping
Dicts map keys to values with O(1) average lookup. Keys must be hashable (immutable).
config = {
"learning_rate": 0.001,
"epochs": 100,
"batch_size": 32,
}
# Access and modify
print(f"LR: {config['learning_rate']}")
config["dropout"] = 0.5
config["epochs"] = 200
# Safe access with .get()
momentum = config.get("momentum", 0.9)
print(f"Momentum: {momentum}")
# Iteration
print("\nAll settings:")
for key, value in config.items():
print(f" {key}: {value}")LR: 0.001
Momentum: 0.9
All settings:
learning_rate: 0.001
epochs: 200
batch_size: 32
dropout: 0.5Dict methods:
| Method | Returns |
|---|---|
d[key] |
Value (raises KeyError if missing) |
d.get(key, default) |
Value or default |
d.keys() |
View of keys |
d.values() |
View of values |
d.items() |
View of (key, value) pairs |
d.pop(key) |
Remove and return value |
d.update(other) |
Merge another dict |
key in d |
Membership test (O(1)) |
Sets: Unique Elements
Sets store unique elements with O(1) membership testing. Based on hash tables like dicts.
# Creating sets
seen_labels = {0, 1, 2, 1, 0} # Duplicates removed
print(f"Unique labels: {seen_labels}")
# From list (common pattern)
data = [1, 2, 2, 3, 3, 3]
unique = set(data)
print(f"Unique values: {unique}")
print(f"Count: {len(unique)}")
# Membership testing (fast!)
if 2 in seen_labels:
print("Label 2 exists")
# Set operations
a = {1, 2, 3, 4}
b = {3, 4, 5, 6}
print(f"Union: {a | b}")
print(f"Intersection: {a & b}")
print(f"Difference: {a - b}")
print(f"Symmetric diff: {a ^ b}")Unique labels: {0, 1, 2}
Unique values: {1, 2, 3}
Count: 3
Label 2 exists
Union: {1, 2, 3, 4, 5, 6}
Intersection: {3, 4}
Difference: {1, 2}
Symmetric diff: {1, 2, 5, 6}When to use sets:
# Finding duplicates
items = ["cat", "dog", "cat", "bird", "dog"]
seen = set()
duplicates = set()
for item in items:
if item in seen:
duplicates.add(item)
seen.add(item)
print(f"Duplicates: {duplicates}")Duplicates: {'cat', 'dog'}Set vs list for membership:
import timeit
data_list = list(range(10000))
data_set = set(range(10000))
t_list = timeit.timeit(lambda: 9999 in data_list, number=1000)
t_set = timeit.timeit(lambda: 9999 in data_set, number=1000)
print(f"List lookup: {t_list*1000:.2f}ms")
print(f"Set lookup: {t_set*1000:.2f}ms")
print(f"Set is {t_list/t_set:.0f}x faster")List lookup: 57.76ms
Set lookup: 0.03ms
Set is 2051x fasterIndexing and Slicing
Zero-based indexing. Negative indices count from the end. Slicing creates copies.

Slice syntax: [start:stop:step]
start: First index (inclusive), default 0stop: Last index (exclusive), default lenstep: Increment, default 1
data = [10, 20, 30, 40, 50, 60, 70]
print(f"data[2:5] = {data[2:5]}") # [30, 40, 50]
print(f"data[:3] = {data[:3]}") # [10, 20, 30]
print(f"data[4:] = {data[4:]}") # [50, 60, 70]
print(f"data[::2] = {data[::2]}") # [10, 30, 50, 70]
print(f"data[::-1] = {data[::-1]}") # Reversed
print(f"data[1:-1] = {data[1:-1]}") # [20, 30, 40, 50, 60]data[2:5] = [30, 40, 50]
data[:3] = [10, 20, 30]
data[4:] = [50, 60, 70]
data[::2] = [10, 30, 50, 70]
data[::-1] = [70, 60, 50, 40, 30, 20, 10]
data[1:-1] = [20, 30, 40, 50, 60]Slicing creates copies (for lists):
original = [1, 2, 3, 4, 5]
copy = original[:] # Shallow copy
copy[0] = 999
print(f"Original: {original}")
print(f"Copy: {copy}")Original: [1, 2, 3, 4, 5]
Copy: [999, 2, 3, 4, 5]Slice assignment (modifies in place):
data = [1, 2, 3, 4, 5]
data[1:4] = [20, 30] # Replace slice
print(f"After: {data}")
data[2:2] = [100, 200] # Insert at index 2
print(f"After insert: {data}")After: [1, 20, 30, 5]
After insert: [1, 20, 100, 200, 30, 5]Warning: NumPy arrays behave differently — slices are views, not copies.
Conditionals and Boolean Logic
Python uses indentation (not braces) to define blocks. Standard is 4 spaces.
score = 0.85
if score >= 0.9:
grade = "A"
elif score >= 0.8:
grade = "B"
elif score >= 0.7:
grade = "C"
else:
grade = "F"
print(grade)BConditional expression (ternary):
Boolean operators use words, not symbols:
| Python | C/Java equivalent |
|---|---|
and |
&& |
or |
\|\| |
not |
! |
Short-circuit evaluation: and/or stop as soon as result is determined.
# Second part not evaluated if first is False
x = None
if x is not None and x > 0:
print("Positive")
else:
print("None or non-positive")None or non-positiveChained comparisons (Python-specific):
Truthiness and Falsy Values
Python evaluates any object in boolean context. Falsy values evaluate to False; everything else is truthy.
Falsy values (memorize these):
| Type | Falsy value |
|---|---|
| Boolean | False |
| None | None |
| Numeric zero | 0, 0.0, 0j, Decimal(0) |
| Empty sequence | "", [], () |
| Empty mapping | {} |
| Empty set | set() |
Everything else is truthy: non-zero numbers, non-empty strings, non-empty collections, objects.
Idiomatic patterns using truthiness:
data = []
# Instead of: if len(data) > 0:
if data:
print("Has items")
else:
print("Empty")
# Default value pattern
name = ""
display_name = name or "Anonymous"
print(f"Hello, {display_name}")
# Guard clause
result = None
value = result or "default"
print(value)Empty
Hello, Anonymous
defaultCaution with or: Returns first truthy value or last value, not necessarily True/False.
For Loops and Iteration
Python’s for iterates over iterables (sequences, generators, files, etc.), not indices. This is fundamentally different from C-style for (i=0; i<n; i++).
Basic iteration:
range() for numeric sequences:
# range(stop), range(start, stop), range(start, stop, step)
print(list(range(5))) # [0, 1, 2, 3, 4]
print(list(range(2, 6))) # [2, 3, 4, 5]
print(list(range(0, 10, 2))) # [0, 2, 4, 6, 8][0, 1, 2, 3, 4]
[2, 3, 4, 5]
[0, 2, 4, 6, 8]range() is lazy — yields values on demand, doesn’t create a list. range(10**9) uses ~48 bytes, not 8 GB.
enumerate() when you need indices:
zip() for parallel iteration:
names = ["Alice", "Bob", "Carol"]
scores = [85, 92, 78]
for name, score in zip(names, scores):
print(f"{name}: {score}")Alice: 85
Bob: 92
Carol: 78Loop control:
| Statement | Effect |
|---|---|
break |
Exit loop immediately |
continue |
Skip to next iteration |
else |
Runs if loop completes without break |
While Loops
Use while when the number of iterations isn’t known in advance, or for event loops.
# Convergence loop (common in optimization)
loss = 1.0
iteration = 0
tolerance = 0.1
while loss > tolerance:
loss *= 0.5
iteration += 1
print(f"Converged in {iteration} iterations")
print(f"Final loss: {loss:.4f}")Converged in 4 iterations
Final loss: 0.0625Infinite loop with break:
for vs while:
for |
while |
|---|---|
| Iterating over a collection | Unknown iteration count |
| Known iteration count | Waiting for condition |
| Processing each element | Event loops |
Infinite loop (loop variable not updated):
Off-by-one (<= vs <):
The walrus operator (:=, Python 3.8+):
Comprehensions
Comprehensions are concise, readable syntax for creating collections from iteration. They replace common for loop patterns.
General form:
[expression for item in iterable if condition]List comprehension:
# Transform each element
squares = [x**2 for x in range(6)]
print(squares)
# Filter elements
evens = [x for x in range(10) if x % 2 == 0]
print(evens)
# Equivalent explicit loop:
# evens = []
# for x in range(10):
# if x % 2 == 0:
# evens.append(x)[0, 1, 4, 9, 16, 25]
[0, 2, 4, 6, 8]Nested comprehension:
Dict and set comprehensions:
# Dict: {key_expr: value_expr for ...}
words = ["cat", "dog", "elephant"]
lengths = {w: len(w) for w in words}
print(lengths)
# Set: {expr for ...}
remainders = {x % 3 for x in range(10)}
print(remainders){'cat': 3, 'dog': 3, 'elephant': 8}
{0, 1, 2}Generator expression (lazy, memory-efficient):
# Parentheses instead of brackets
gen = (x**2 for x in range(1000000))
print(type(gen))
print(sum(gen)) # Computed on-demand<class 'generator'>
333332833333500000Performance: Comprehensions are ~10-20% faster than equivalent for loops (append is inlined in bytecode).
Defining Functions
Functions are defined with def. The first string literal becomes __doc__ (accessible via help()).
def compute_accuracy(correct, total):
"""Compute classification accuracy."""
return correct / total
print(compute_accuracy(85, 100))0.85Function structure:
- No return type declaration
- No
returnstatement → returnsNone - Functions are objects (can be assigned, passed, returned)
Function Arguments
Positional vs keyword:
def train(model, lr, epochs):
print(f"model={model}, lr={lr}, epochs={epochs}")
train("resnet", 0.01, 100) # Positional
train("resnet", epochs=50, lr=0.001) # Keyword (any order)
train("resnet", 0.01, epochs=200) # Mixedmodel=resnet, lr=0.01, epochs=100
model=resnet, lr=0.001, epochs=50
model=resnet, lr=0.01, epochs=200Variadic arguments:
| Syntax | Captures |
|---|---|
*args |
Extra positional → tuple |
**kwargs |
Extra keyword → dict |
def log_call(name, *args, **kwargs):
print(f"Function: {name}")
print(f" args: {args}")
print(f" kwargs: {kwargs}")
log_call("train", 100, 0.01, lr=0.001, verbose=True)Function: train
args: (100, 0.01)
kwargs: {'lr': 0.001, 'verbose': True}Argument order in signature:
- Regular positional
*args- Keyword-only (after
*) **kwargs
Mutable Default Arguments
Default values are evaluated once at function definition, not per call.
Shared mutable default:
Classes
Classes bundle data (attributes) with behavior (methods).
class Layer:
def __init__(self, in_size, out_size):
self.in_size = in_size
self.out_size = out_size
def num_params(self):
return self.in_size * self.out_size + self.out_size
def __repr__(self):
return f"Layer({self.in_size}, {self.out_size})"
layer = Layer(784, 256)
print(layer)
print(f"Parameters: {layer.num_params():,}")Layer(784, 256)
Parameters: 200,960Special methods (dunder methods):
| Method | Called by |
|---|---|
__init__ |
Layer(...) (constructor) |
__repr__ |
repr(obj), debugger display |
__str__ |
str(obj), print(obj) |
__len__ |
len(obj) |
__getitem__ |
obj[key] |
__call__ |
obj(...) (callable) |
self: Explicit reference to instance (like this in C++/Java, but explicit in signature).
Attributes: Created by assignment to self.name — no declaration needed.
Modules and Imports
Module = Python file. Package = directory with __init__.py.
Import styles:
import math # Entire module
print(math.sqrt(2))
import numpy as np # Alias
from collections import Counter # Specific name
print(Counter("abracadabra"))1.4142135623730951
Counter({'a': 5, 'b': 2, 'r': 2, 'c': 1, 'd': 1})| Style | Access | Namespace |
|---|---|---|
import mod |
mod.func() |
Separate |
import mod as m |
m.func() |
Aliased |
from mod import func |
func() |
Merged |
from mod import * |
All names | Pollutes (avoid) |
Exception Handling
try/except structure:
def safe_divide(a, b):
try:
return a / b
except ZeroDivisionError:
return float('inf')
print(safe_divide(10, 2))
print(safe_divide(10, 0))5.0
infCatching with details:
Full syntax:
try:
risky_operation()
except ValueError as e:
handle_value_error(e)
except (TypeError, KeyError):
handle_other()
else:
# Runs if no exception
success()
finally:
# Always runs (cleanup)
close_resources()Raising exceptions:
Common exceptions:
| Exception | Cause |
|---|---|
ValueError |
Wrong value |
TypeError |
Wrong type |
KeyError |
Missing dict key |
IndexError |
Index out of range |
AttributeError |
Missing attribute |
Built-in Functions
Aggregation:
| Function | Description |
|---|---|
len(x) |
Length/size |
sum(x) |
Sum elements |
min(x), max(x) |
Minimum/maximum |
sorted(x) |
Sorted copy |
reversed(x) |
Reverse iterator |
Type operations:
| Function | Description |
|---|---|
type(x) |
Type of object |
isinstance(x, t) |
Type check |
int(), float(), str() |
Conversion |
list(), tuple(), set() |
Collection conversion |
Boolean:
| Function | Description |
|---|---|
any(x) |
True if any truthy |
all(x) |
True if all truthy |
bool(x) |
Convert to boolean |
Numeric:
| Function | Description |
|---|---|
abs(x) |
Absolute value |
round(x, n) |
Round to n decimals |
pow(x, y) |
x^y (or x ** y) |
divmod(a, b) |
(a // b, a % b) |
Iteration:
| Function | Description |
|---|---|
range(n) |
0, 1, …, n-1 |
enumerate(x) |
(index, value) pairs |
zip(a, b) |
Parallel iteration |
map(f, x) |
Apply f to each |
filter(f, x) |
Keep where f(x) true |
Type Hints
Type hints document expected types. Not enforced at runtime — for documentation and static analysis (mypy).
Syntax (Python 3.10+):
| Type | Meaning |
|---|---|
int, float, str |
Basic types |
list[int] |
List of ints |
dict[str, float] |
Dict with str keys |
tuple[int, str] |
Fixed-length tuple |
int \| None |
Union (or Optional[int]) |
Callable[[int], str] |
Function type |
Any |
Disable type checking |
Checking with mypy:
Benefits: IDE autocompletion, catch type errors before runtime, self-documenting signatures.
Data Structure Internals
Sequence Types: Three Design Choices
Python provides three sequence types with different trade-offs.

Design Consequences:
- Lists allow heterogeneous data but pay indirection cost
- Tuples trade mutability for hashability and memory efficiency
- Strings optimize for text with specialized methods
import sys
# Memory comparison
lst = [1, 2, 3, 4, 5]
tup = (1, 2, 3, 4, 5)
string = "12345"
print("Memory usage:")
print(f" List: {sys.getsizeof(lst)} bytes")
print(f" Tuple: {sys.getsizeof(tup)} bytes")
print(f" String: {sys.getsizeof(string)} bytes")
# Hashability determines dict key eligibility
print("\nCan be dict key:")
for obj, name in [(lst, 'List'), (tup, 'Tuple'), (string, 'String')]:
try:
d = {obj: 'value'}
print(f" {name}: Yes")
except TypeError:
print(f" {name}: No")Memory usage:
List: 104 bytes
Tuple: 80 bytes
String: 54 bytes
Can be dict key:
List: No
Tuple: Yes
String: YesList Internals: Over-allocation Strategy
Lists allocate extra space to amortize the cost of growth.

# Observe allocation behavior
import sys
lst = []
sizes_and_caps = []
for i in range(20):
lst.append(i)
# Size includes list object overhead
total_size = sys.getsizeof(lst)
# Approximate capacity from size
capacity = (total_size - sys.getsizeof([])) // 8
sizes_and_caps.append((len(lst), capacity))
# Show growth points
print("Size → Capacity:")
last_cap = 0
for size, cap in sizes_and_caps:
if cap != last_cap:
print(f" {size:2d} → {cap:2d} (grew by {cap - last_cap})")
last_cap = capSize → Capacity:
1 → 4 (grew by 4)
5 → 8 (grew by 4)
9 → 16 (grew by 8)
17 → 24 (grew by 8)Growth Strategy:
When a list exceeds capacity, Python:
- Calculates new capacity using formula
- Allocates new pointer array
- Copies all existing pointers
- Frees old array
Cost Analysis:
- Append is O(1) amortized
- Individual append can trigger O(n) reallocation
- Trade memory for performance
List Operations: Implementation Details
Different operations have different costs based on internal structure.

# Demonstrating operation costs
import time
def measure_operation(lst, operation, description):
"""Measure single operation time."""
start = time.perf_counter()
operation(lst)
elapsed = time.perf_counter() - start
return elapsed * 1e6 # Convert to microseconds
# Large list for measurable times
n = 100000
test_list = list(range(n))
# Operations
times = {}
times['append'] = measure_operation(test_list.copy(),
lambda l: l.append(999),
"Append")
times['insert_0'] = measure_operation(test_list.copy(),
lambda l: l.insert(0, 999),
"Insert at 0")
times['pop'] = measure_operation(test_list.copy(),
lambda l: l.pop(),
"Pop from end")
times['pop_0'] = measure_operation(test_list.copy(),
lambda l: l.pop(0),
"Pop from start")
print(f"Operation times (n={n}):")
for op, time in times.items():
print(f" {op:12s}: {time:8.2f} μs")Operation times (n=100000):
append : 0.79 μs
insert_0 : 31.33 μs
pop : 0.33 μs
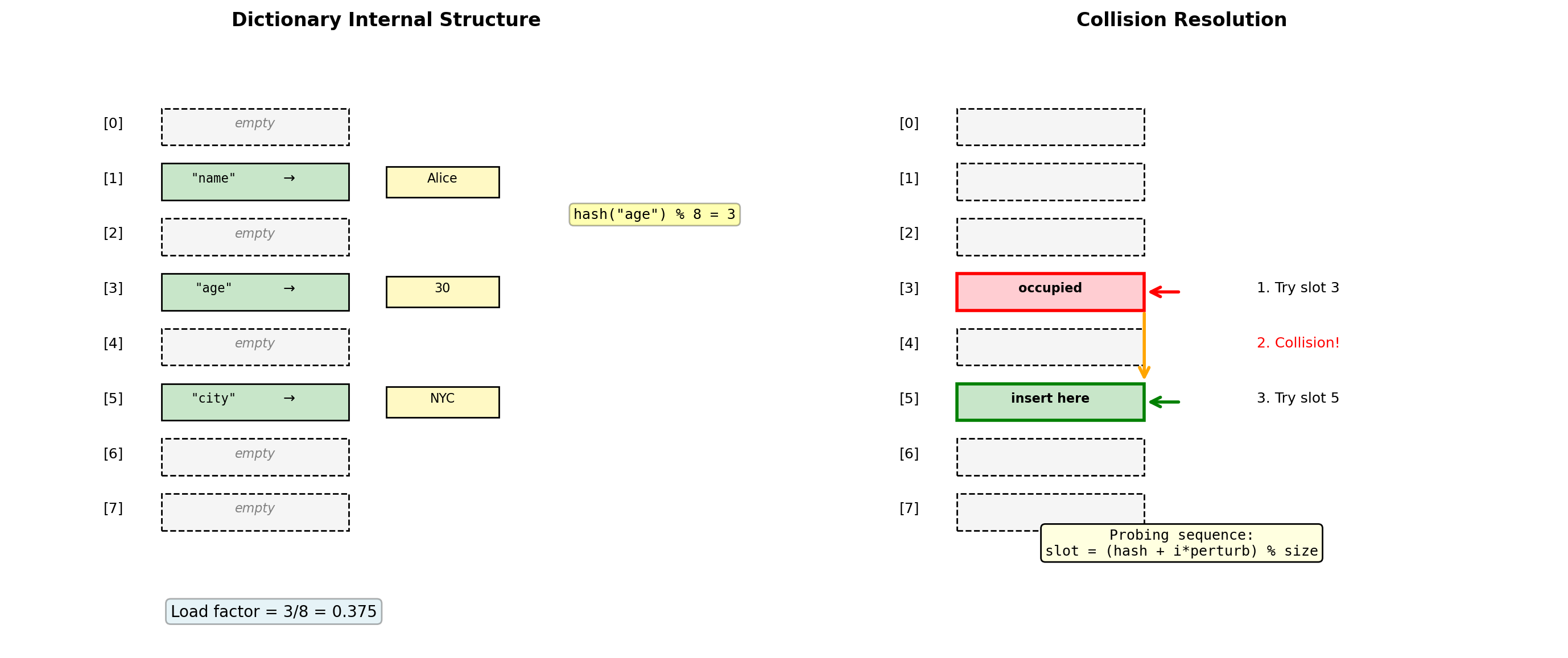
pop_0 : 14.33 μsDictionary Architecture: Open Addressing Hash Table
Dictionaries use open addressing with random probing for collision resolution.
# Dictionary internals
d = {'a': 1, 'b': 2, 'c': 3}
# Show hash values
for key in d:
print(f"hash('{key}') = {hash(key):20d}")
# Dictionary growth
import sys
sizes = []
for i in range(20):
d = {str(j): j for j in range(i)}
sizes.append((i, sys.getsizeof(d)))
print("\nDict size growth:")
last_size = 0
for n, size in sizes:
if size != last_size:
print(f" {n:2d} items: {size:4d} bytes")
last_size = sizehash('a') = -8650723016916319182
hash('b') = 6464835138523459154
hash('c') = 1984612578382285418
Dict size growth:
0 items: 64 bytes
1 items: 184 bytes
6 items: 272 bytes
11 items: 464 bytesDesign Choices:
- Open addressing: No separate chains, better cache locality
- 2/3 load factor: Resize when 2/3 full
- Perturbed probing: Reduces clustering
- Cached hash values: Store hash with key to avoid recomputation
Consequences:
- O(1) average case for all operations
- Order preserved since Python 3.7
- More memory than theoretical minimum
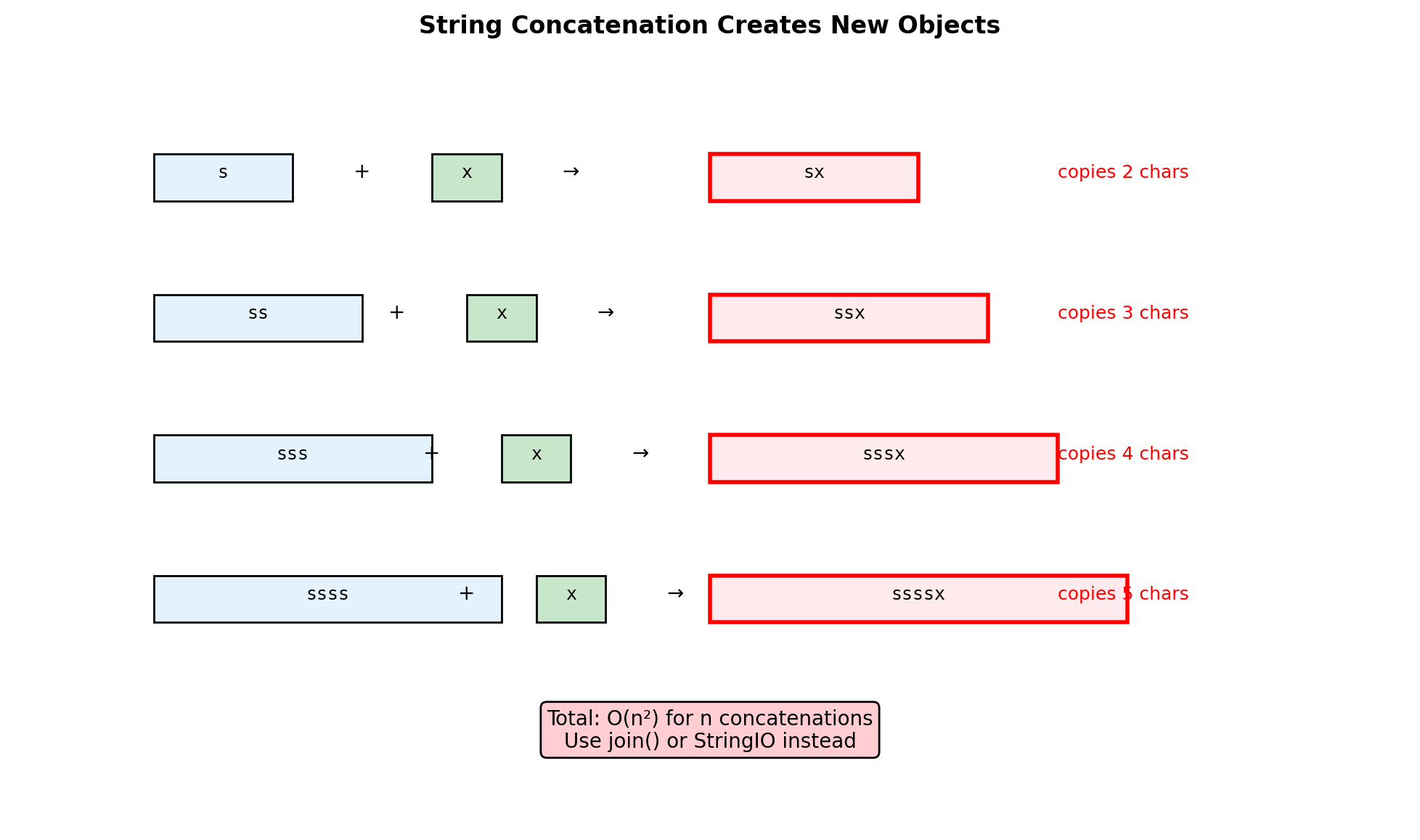
String Building: Algorithmic Complexity
Building strings efficiently requires understanding concatenation costs.
import io
import timeit
n = 1000
chunk = "x" * 10
# Method 1: Repeated concatenation (BAD)
def build_concat():
s = ""
for _ in range(n):
s += chunk # Creates new string each time
return s
# Method 2: Join (GOOD)
def build_join():
parts = []
for _ in range(n):
parts.append(chunk)
return "".join(parts)
# Method 3: StringIO (GOOD)
def build_io():
buffer = io.StringIO()
for _ in range(n):
buffer.write(chunk)
return buffer.getvalue()
# Compare performance
t1 = timeit.timeit(build_concat, number=100)
t2 = timeit.timeit(build_join, number=100)
t3 = timeit.timeit(build_io, number=100)
print(f"Building {n}-chunk string (100 iterations):")
print(f" Concatenation: {t1:.4f}s")
print(f" Join: {t2:.4f}s ({t1/t2:.1f}x faster)")
print(f" StringIO: {t3:.4f}s ({t1/t3:.1f}x faster)")Building 1000-chunk string (100 iterations):
Concatenation: 0.0035s
Join: 0.0017s (2.1x faster)
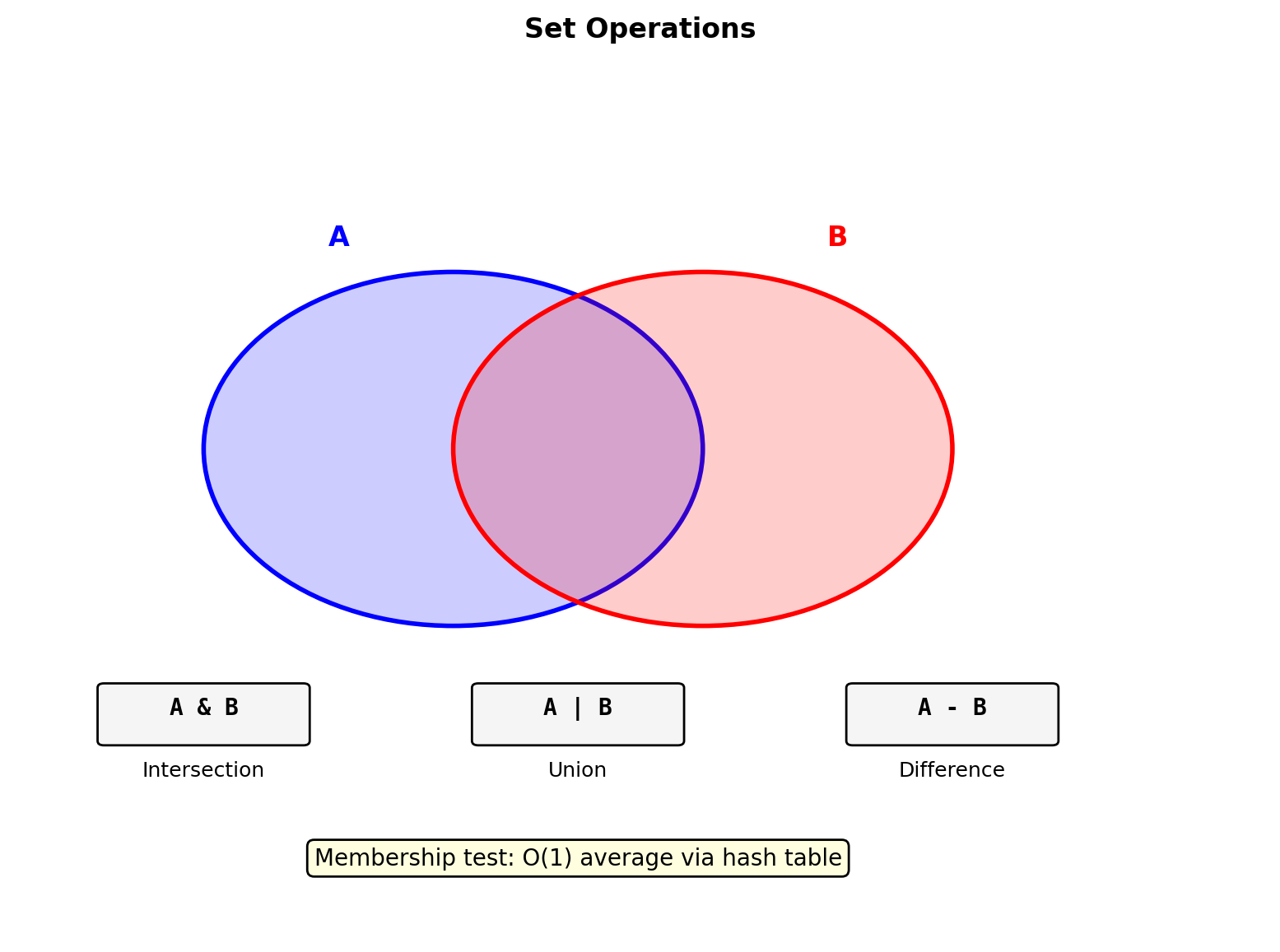
StringIO: 0.0029s (1.2x faster)Collection Internals: Sets and Frozen Sets
Sets use the same hash table technology as dictionaries, optimized for membership testing.
# Set performance demonstration
import random
# Create test data
numbers = list(range(10000))
random.shuffle(numbers)
test_list = numbers[:5000]
test_set = set(test_list)
# Membership testing
lookups = random.sample(range(10000), 100)
import time
# List lookup
start = time.perf_counter()
for x in lookups:
_ = x in test_list
list_time = time.perf_counter() - start
# Set lookup
start = time.perf_counter()
for x in lookups:
_ = x in test_set
set_time = time.perf_counter() - start
print(f"100 lookups in collection of 5000:")
print(f" List: {list_time*1000:.3f} ms")
print(f" Set: {set_time*1000:.3f} ms")
print(f" Speedup: {list_time/set_time:.1f}x")
# Set operations
a = {1, 2, 3, 4, 5}
b = {4, 5, 6, 7, 8}
print(f"\nSet operations:")
print(f" a & b = {a & b}") # Intersection
print(f" a | b = {a | b}") # Union
print(f" a - b = {a - b}") # Difference
print(f" a ^ b = {a ^ b}") # Symmetric difference100 lookups in collection of 5000:
List: 2.265 ms
Set: 0.024 ms
Speedup: 96.0x
Set operations:
a & b = {4, 5}
a | b = {1, 2, 3, 4, 5, 6, 7, 8}
a - b = {1, 2, 3}
a ^ b = {1, 2, 3, 6, 7, 8}Set Implementation:
- Same hash table as dict (no values)
- Average O(1) for add, remove, membership
- Set operations optimized with early termination
- Frozen sets are immutable and hashable
When to use sets:
- Membership testing in loops
- Removing duplicates
- Mathematical set operations
- When order doesn’t matter
Memory overhead:
- Minimum size: 8 slots
- Growth factor: 4x until 50k, then 2x
- ~30% more memory than list of same items
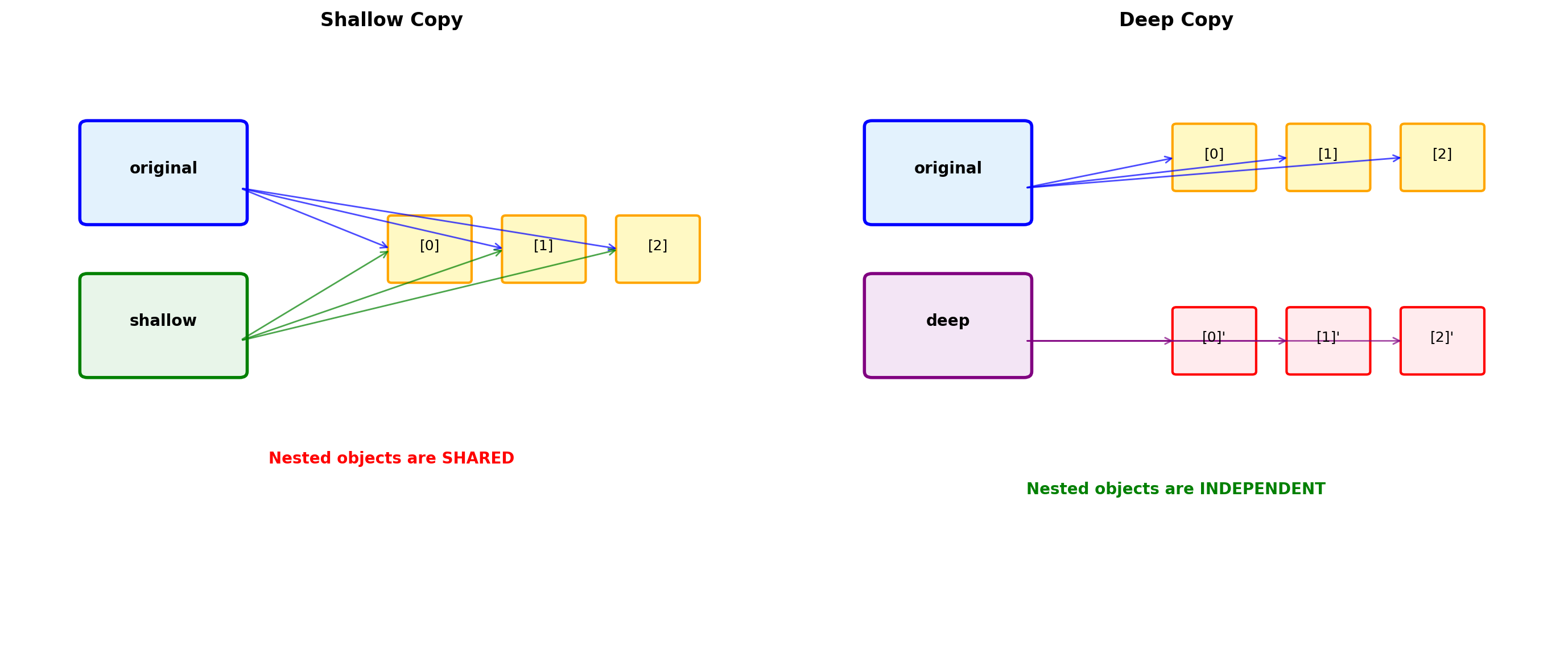
Shallow vs Deep Copying
Python’s default copying behavior can lead to unexpected aliasing.
import copy
# Create nested structure
original = [[1, 2], [3, 4], [5, 6]]
# Different copy methods
reference = original
shallow = original.copy() # or list(original) or original[:]
deep = copy.deepcopy(original)
# Modify nested object
original[0].append(3)
print("After modifying original[0]:")
print(f" original: {original}")
print(f" reference: {reference}") # Changed
print(f" shallow: {shallow}") # Changed!
print(f" deep: {deep}") # Unchanged
# Identity checks
print("\nIdentity comparisons:")
print(f" original is reference: {original is reference}")
print(f" original is shallow: {original is shallow}")
print(f" original[0] is shallow[0]: {original[0] is shallow[0]}") # True!
print(f" original[0] is deep[0]: {original[0] is deep[0]}") # FalseAfter modifying original[0]:
original: [[1, 2, 3], [3, 4], [5, 6]]
reference: [[1, 2, 3], [3, 4], [5, 6]]
shallow: [[1, 2, 3], [3, 4], [5, 6]]
deep: [[1, 2], [3, 4], [5, 6]]
Identity comparisons:
original is reference: True
original is shallow: False
original[0] is shallow[0]: True
original[0] is deep[0]: FalseAbstraction and Design
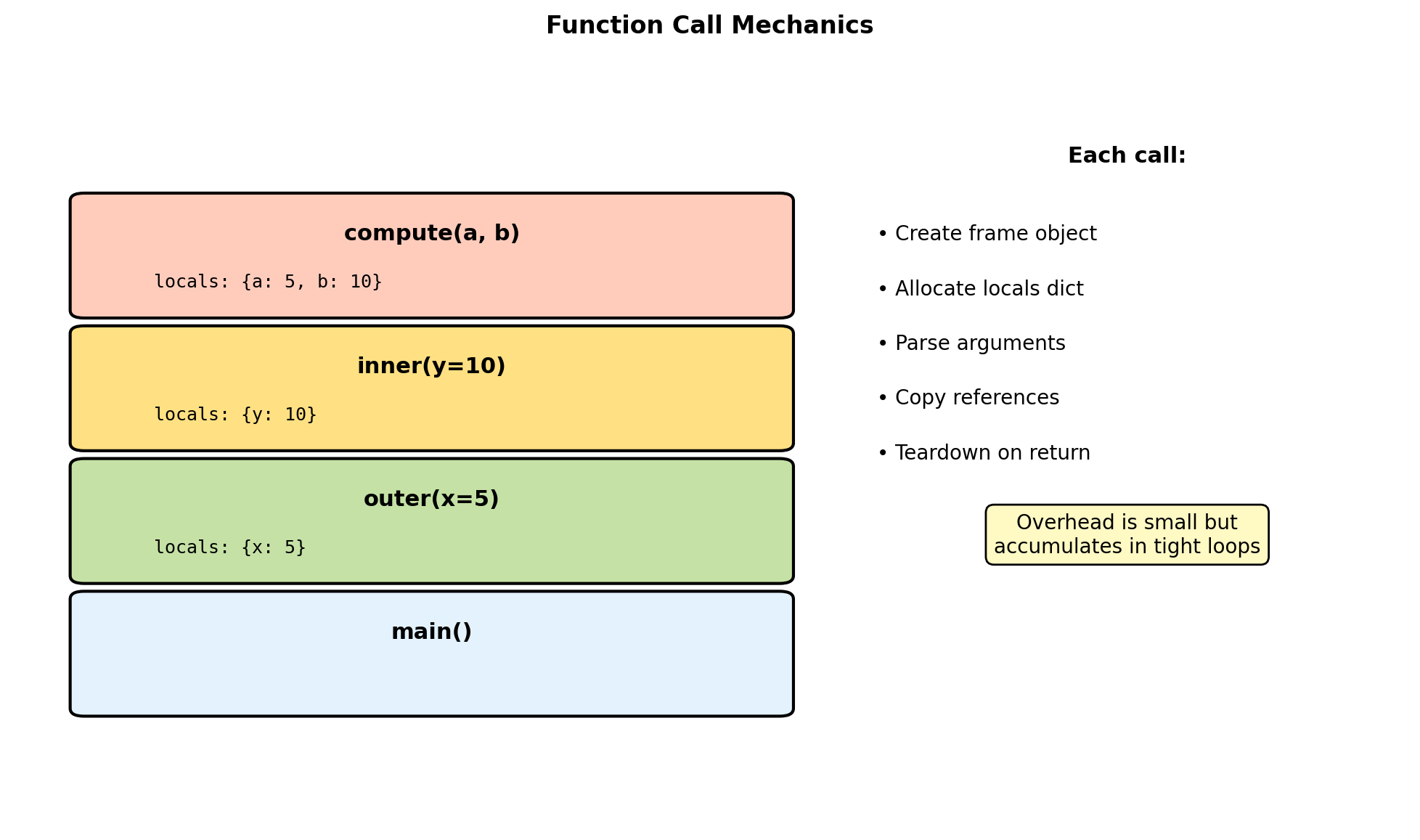
Function Call Overhead
import timeit
def add_function(x, y):
return x + y
add_lambda = lambda x, y: x + y
# Direct operation
def test_inline():
total = 0
for i in range(1000):
total += i + 1
return total
# Function call
def test_function():
total = 0
for i in range(1000):
total += add_function(i, 1)
return total
# Lambda call
def test_lambda():
total = 0
for i in range(1000):
total += add_lambda(i, 1)
return total
n = 10000
t_inline = timeit.timeit(test_inline, number=n)
t_func = timeit.timeit(test_function, number=n)
t_lambda = timeit.timeit(test_lambda, number=n)
print(f"1000 additions, {n} iterations:")
print(f" Inline: {t_inline:.3f}s")
print(f" Function: {t_func:.3f}s ({t_func/t_inline:.1f}x)")
print(f" Lambda: {t_lambda:.3f}s ({t_lambda/t_inline:.1f}x)")1000 additions, 10000 iterations:
Inline: 0.217s
Function: 0.346s (1.6x)
Lambda: 0.342s (1.6x)Call overhead includes:
- Frame object allocation (~100ns)
- Argument parsing and binding (~50ns)
- Namespace setup (~30ns)
- Exception context (~20ns)
Optimization strategies:
- Cache method lookups outside loops
- Use list comprehensions (C loop)
- Vectorize with NumPy
- Consider
@jitfor numerical code
Closures and Captured State
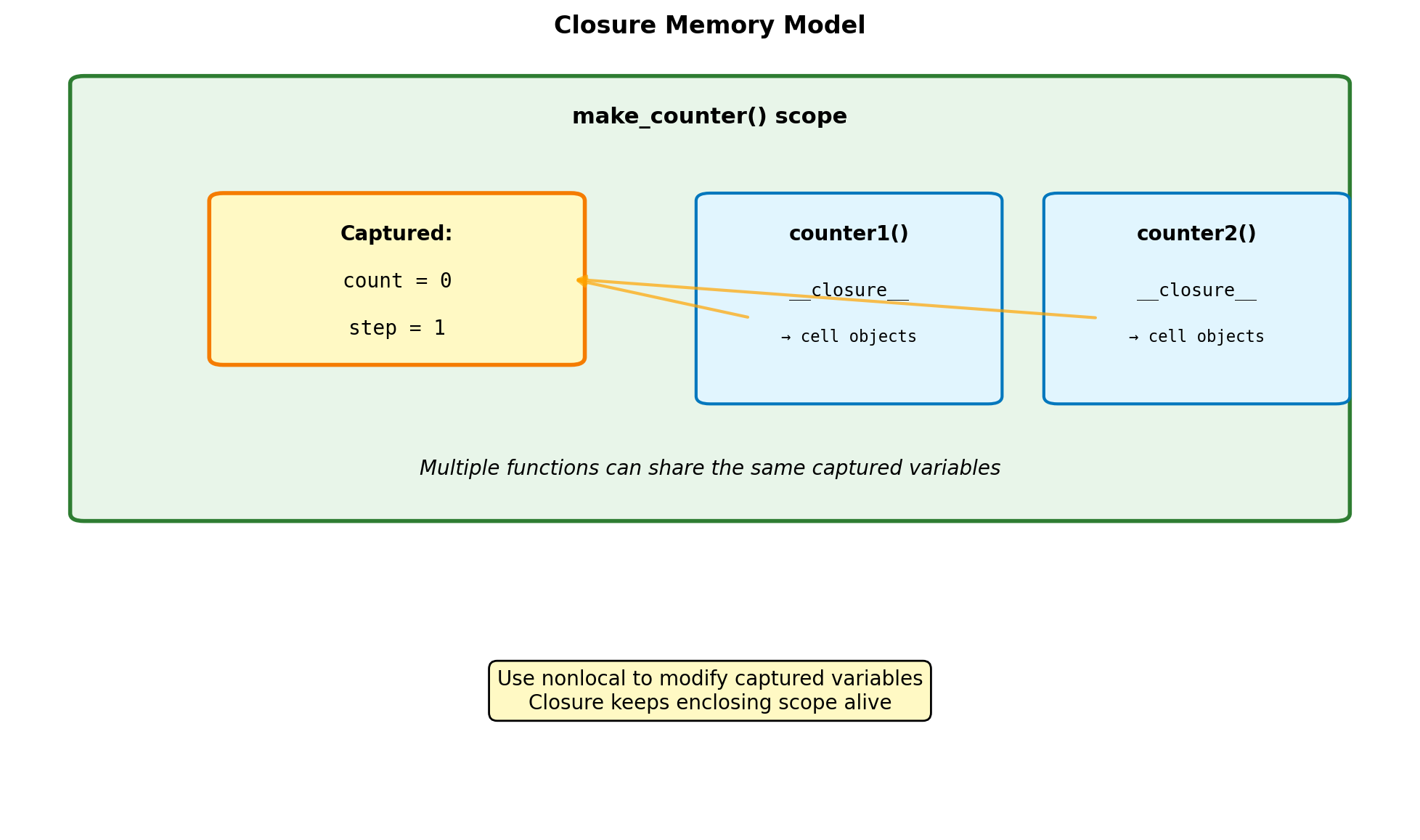
def make_counter(initial=0):
count = initial
def increment(step=1):
nonlocal count
count += step
return count
def get_value():
return count
# Functions share the closure
increment.get = get_value
return increment
# Create closures
counter1 = make_counter()
counter2 = make_counter(100)
print("Separate closures:")
print(f" counter1(): {counter1()}")
print(f" counter1(): {counter1()}")
print(f" counter2(): {counter2()}")
# Inspect closure
import inspect
closure = inspect.getclosurevars(counter1)
print(f"\nClosure variables: {closure.nonlocals}")
# Shared state demonstration
def make_accumulator():
data = []
def add(x):
data.append(x)
return sum(data)
def reset():
data.clear()
add.reset = reset
return add
acc = make_accumulator()
print(f"\nacc(5): {acc(5)}")
print(f"acc(3): {acc(3)}")Separate closures:
counter1(): 1
counter1(): 2
counter2(): 101
Closure variables: {'count': 2}
acc(5): 5
acc(3): 8# Performance impact of closures
import timeit
# Global state
global_counter = 0
def increment_global():
global global_counter
global_counter += 1
return global_counter
# Closure state
def make_closure_counter():
counter = 0
def increment():
nonlocal counter
counter += 1
return counter
return increment
closure_inc = make_closure_counter()
# Class state
class ClassCounter:
def __init__(self):
self.counter = 0
def increment(self):
self.counter += 1
return self.counter
class_counter = ClassCounter()
# Measure
n = 100000
t_global = timeit.timeit(increment_global, number=n)
t_closure = timeit.timeit(closure_inc, number=n)
t_class = timeit.timeit(class_counter.increment, number=n)
print(f"\n{n} increments:")
print(f" Global: {t_global:.3f}s")
print(f" Closure: {t_closure:.3f}s")
print(f" Class: {t_class:.3f}s")
100000 increments:
Global: 0.003s
Closure: 0.003s
Class: 0.003sDecorators: Function Transformation
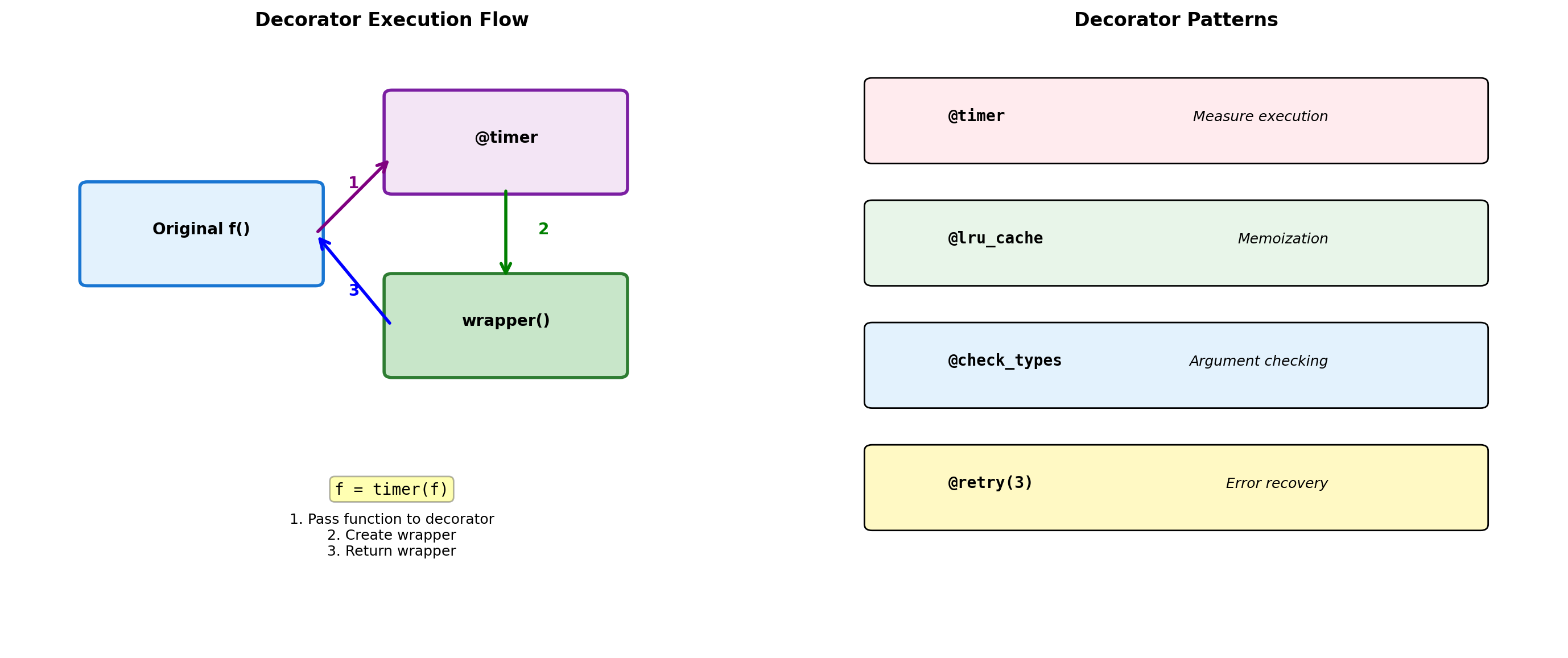
import time
import functools
def timer(func):
"""Decorator to measure execution time."""
@functools.wraps(func)
def wrapper(*args, **kwargs):
start = time.perf_counter()
result = func(*args, **kwargs)
elapsed = time.perf_counter() - start
print(f"{func.__name__}: {elapsed:.4f}s")
return result
return wrapper
def cache(func):
"""Simple memoization decorator."""
memo = {}
@functools.wraps(func)
def wrapper(*args):
if args in memo:
return memo[args]
result = func(*args)
memo[args] = result
return result
wrapper.cache = memo # Expose cache
return wrapper
@timer
@cache
def fibonacci(n):
if n < 2:
return n
return fibonacci(n-1) + fibonacci(n-2)
# First call builds cache
result = fibonacci(10)
print(f"fibonacci(10) = {result}")
# Check cache
print(f"Cache size: {len(fibonacci.cache)}")fibonacci: 0.0000s
fibonacci: 0.0000s
fibonacci: 0.0000s
fibonacci: 0.0000s
fibonacci: 0.0000s
fibonacci: 0.0000s
fibonacci: 0.0000s
fibonacci: 0.0000s
fibonacci: 0.0000s
fibonacci: 0.0000s
fibonacci: 0.0000s
fibonacci: 0.0000s
fibonacci: 0.0001s
fibonacci: 0.0000s
fibonacci: 0.0001s
fibonacci: 0.0000s
fibonacci: 0.0001s
fibonacci: 0.0000s
fibonacci: 0.0001s
fibonacci(10) = 55
Cache size: 11# Parameterized decorator
def validate_range(min_val, max_val):
def decorator(func):
@functools.wraps(func)
def wrapper(x):
if not min_val <= x <= max_val:
raise ValueError(f"{x} not in [{min_val}, {max_val}]")
return func(x)
return wrapper
return decorator
@validate_range(0, 1)
def probability(p):
return f"P = {p}"
print(probability(0.5))
try:
probability(1.5)
except ValueError as e:
print(f"Error: {e}")
# Stack decorators for composition
def logged(func):
@functools.wraps(func)
def wrapper(*args):
print(f"Calling {func.__name__}{args}")
return func(*args)
return wrapper
@logged
@validate_range(-1, 1)
def cosine(x):
import math
return math.cos(math.pi * x)
result = cosine(0.5)
print(f"cos(0.5π) = {result}")P = 0.5
Error: 1.5 not in [0, 1]
Calling cosine(0.5,)
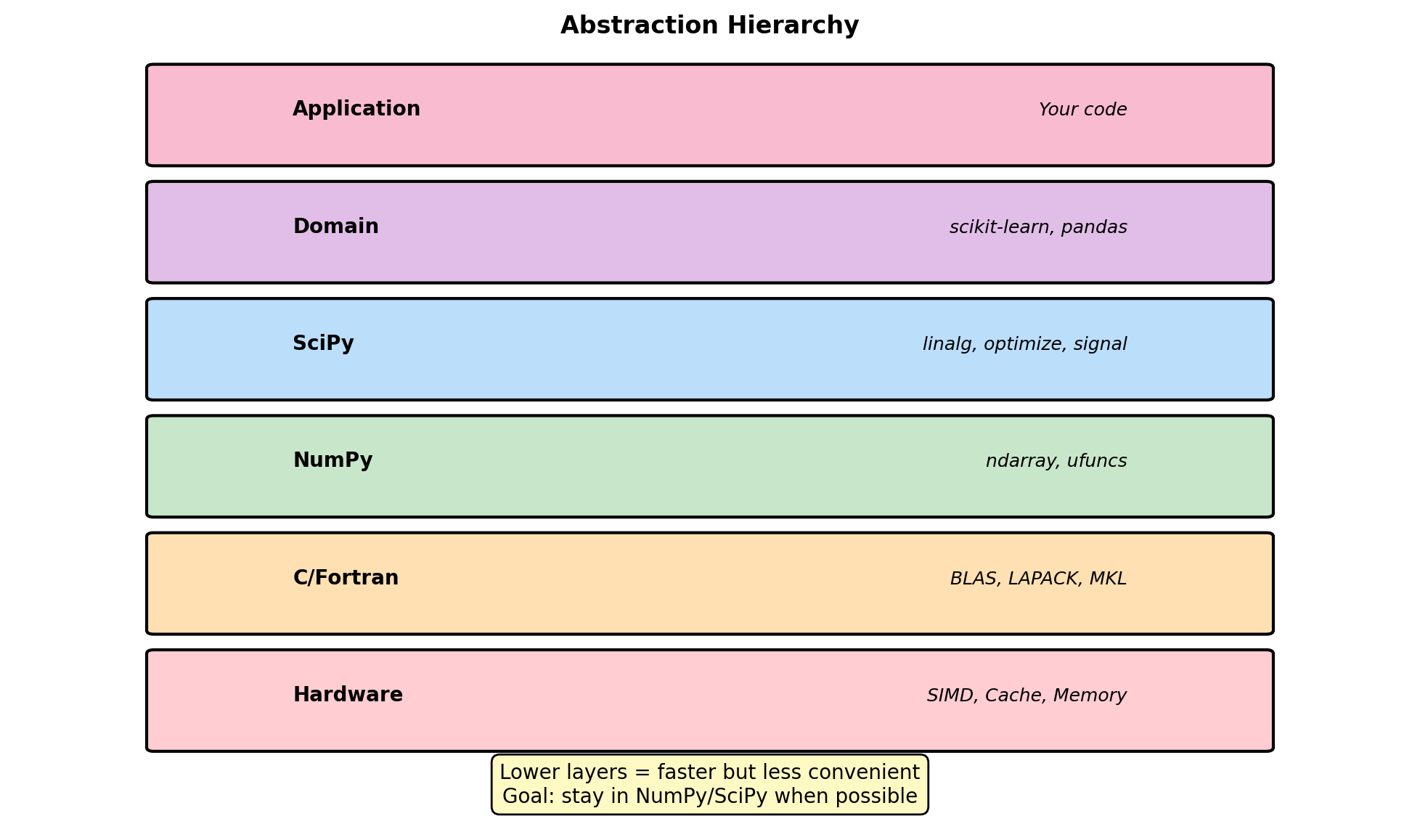
cos(0.5π) = 6.123233995736766e-17Abstraction Layers in Numerical Code
import numpy as np
import timeit
# Three abstraction levels
def python_dot(a, b):
"""Pure Python dot product."""
total = 0
for i in range(len(a)):
total += a[i] * b[i]
return total
def numpy_dot(a, b):
"""NumPy dot product."""
return np.dot(a, b)
# Attempt to import numba (may not be available)
try:
from numba import jit
@jit(nopython=True)
def numba_dot(a, b):
"""JIT-compiled dot product."""
total = 0.0
for i in range(len(a)):
total += a[i] * b[i]
return total
has_numba = True
except ImportError:
has_numba = False
numba_dot = None
# Test different sizes
for size in [10, 100, 1000, 10000]:
list_a = list(range(size))
list_b = list(range(size))
arr_a = np.array(list_a, dtype=float)
arr_b = np.array(list_b, dtype=float)
t_python = timeit.timeit(
lambda: python_dot(list_a, list_b), number=100
)
t_numpy = timeit.timeit(
lambda: numpy_dot(arr_a, arr_b), number=100
)
print(f"Size {size:5d}:")
print(f" Python: {t_python*10:.3f} ms")
print(f" NumPy: {t_numpy*10:.3f} ms ({t_python/t_numpy:.0f}x)")
if has_numba and size <= 1000:
t_numba = timeit.timeit(
lambda: numba_dot(arr_a, arr_b), number=100
)
print(f" Numba: {t_numba*10:.3f} ms ({t_python/t_numba:.0f}x)")Size 10:
Python: 0.000 ms
NumPy: 0.000 ms (1x)
Size 100:
Python: 0.002 ms
NumPy: 0.001 ms (2x)
Size 1000:
Python: 0.026 ms
NumPy: 0.000 ms (55x)
Size 10000:
Python: 0.278 ms
NumPy: 0.002 ms (145x)Abstraction trade-offs:
Each layer adds overhead but provides:
- Higher-level operations
- Better maintainability
- Platform independence
- Automatic optimization
When to drop down a level:
- Inner loops with millions of iterations
- Custom algorithms not in libraries
- Memory-constrained environments
- Real-time requirements
Vectorization threshold:
- NumPy overhead ~1μs
- Break-even around 10-100 elements
- Always profile before optimizing
Generator Patterns for Memory Efficiency
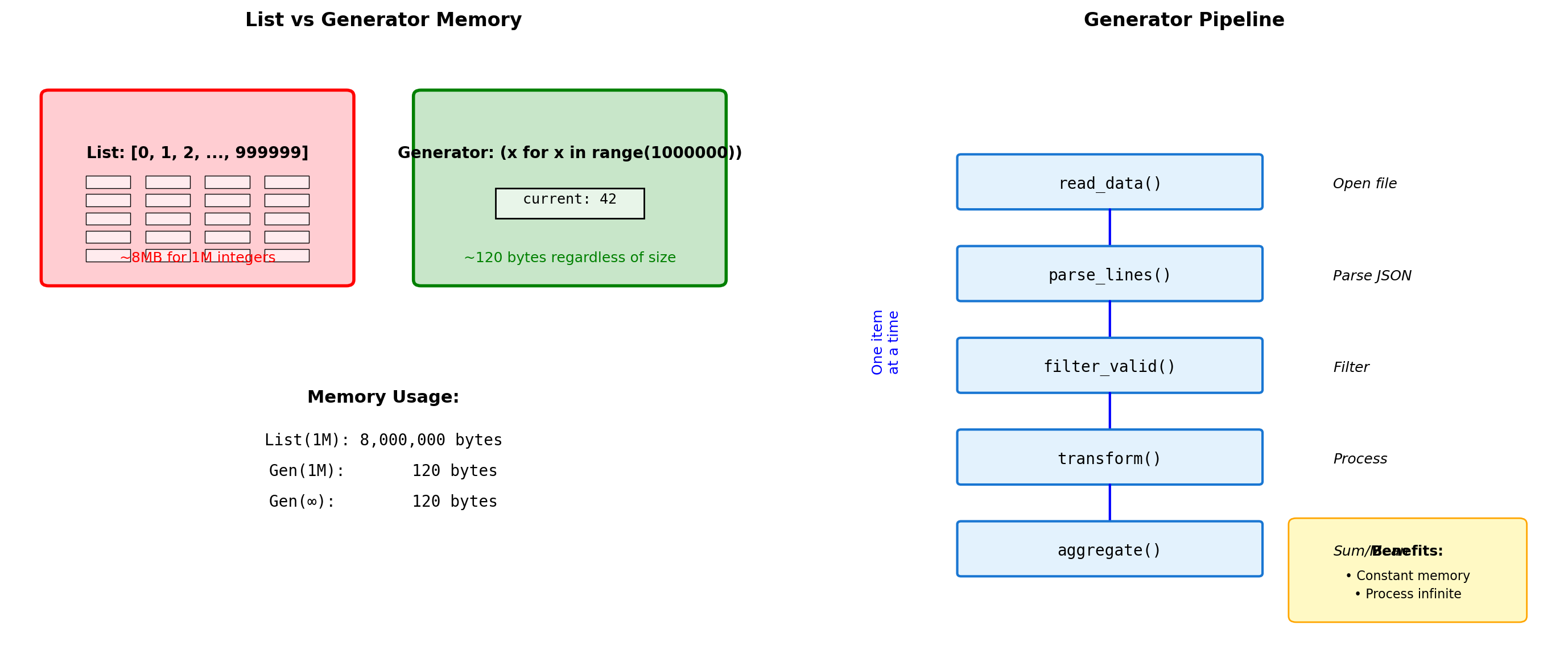
import sys
# Memory comparison
def list_squares(n):
"""Returns list of squares."""
return [x**2 for x in range(n)]
def gen_squares(n):
"""Yields squares one at a time."""
for x in range(n):
yield x**2
# Create both
n = 1000000
squares_list = list_squares(n)
squares_gen = gen_squares(n)
print(f"Memory usage:")
print(f" List: {sys.getsizeof(squares_list):,} bytes")
print(f" Gen: {sys.getsizeof(squares_gen):,} bytes")
# Generator expressions
gen_expr = (x**2 for x in range(n))
print(f" Expr: {sys.getsizeof(gen_expr):,} bytes")
# Pipeline example
def read_numbers(filename):
"""Simulate reading numbers from file."""
for i in range(100):
yield i
def process_pipeline():
"""Chain generators for processing."""
numbers = read_numbers("data.txt")
squared = (x**2 for x in numbers)
filtered = (x for x in squared if x % 2 == 0)
result = sum(filtered) # Only here we consume
return result
result = process_pipeline()
print(f"\nPipeline result: {result}")Memory usage:
List: 8,448,728 bytes
Gen: 208 bytes
Expr: 208 bytes
Pipeline result: 161700# Infinite sequences
def fibonacci():
"""Infinite Fibonacci generator."""
a, b = 0, 1
while True:
yield a
a, b = b, a + b
# Take only what's needed
fib = fibonacci()
first_10 = [next(fib) for _ in range(10)]
print(f"First 10 Fibonacci: {first_10}")
# Generator with state
def running_average():
"""Maintains running average."""
total = 0
count = 0
while True:
value = yield total / count if count else 0
if value is not None:
total += value
count += 1
avg = running_average()
next(avg) # Prime the generator
print(f"\nRunning average:")
for val in [10, 20, 30, 40]:
result = avg.send(val)
print(f" Added {val}, average: {result:.1f}")
# Memory-efficient file processing
def process_large_file(filename):
"""Process file without loading it all."""
with open(filename, 'r') as f:
for line in f: # Generator, not list
if line.strip():
yield line.strip().upper()First 10 Fibonacci: [0, 1, 1, 2, 3, 5, 8, 13, 21, 34]
Running average:
Added 10, average: 10.0
Added 20, average: 15.0
Added 30, average: 20.0
Added 40, average: 25.0Composition vs Inheritance
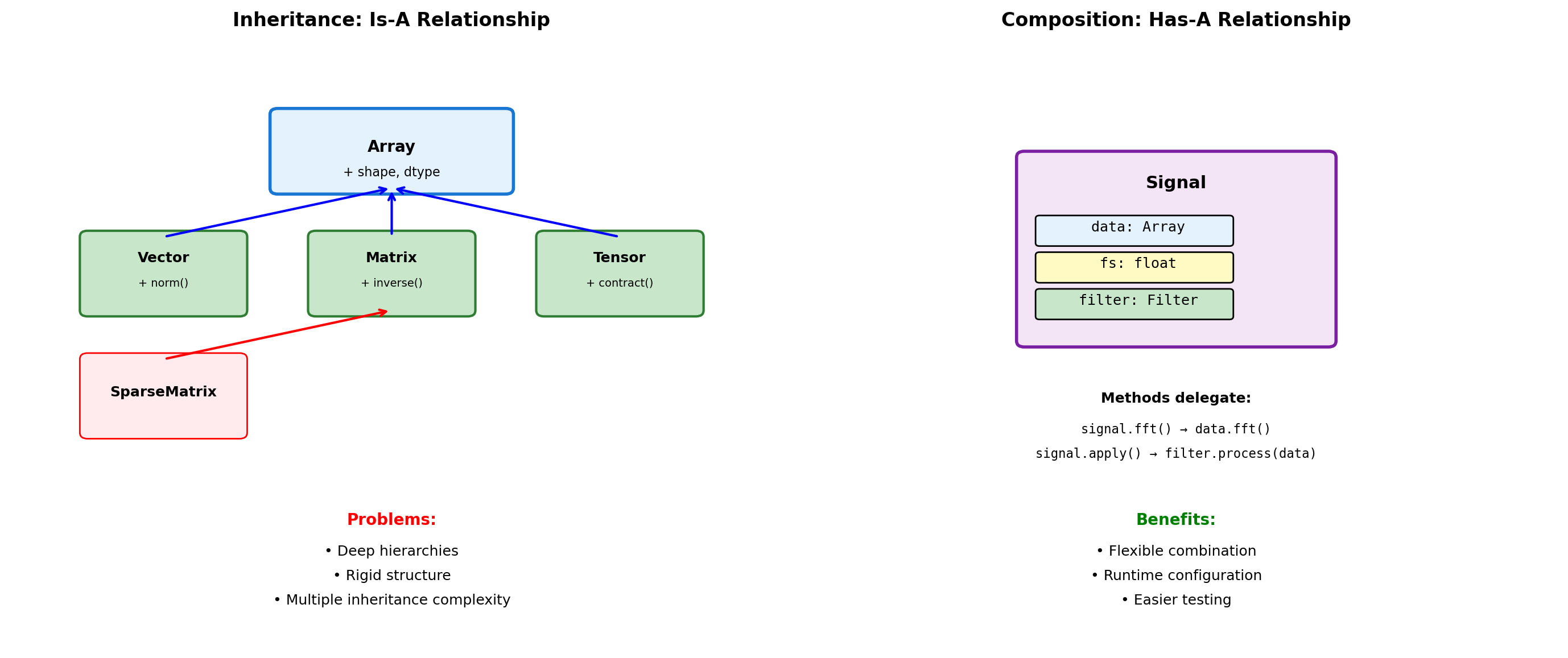
# Inheritance approach
class Vector(list):
"""Vector inherits from list."""
def __init__(self, components):
super().__init__(components)
def magnitude(self):
return sum(x**2 for x in self) ** 0.5
def dot(self, other):
return sum(a*b for a, b in zip(self, other))
# Problems with inheritance
v = Vector([3, 4])
print(f"Vector: {v}")
print(f"Magnitude: {v.magnitude()}")
# But inherits unwanted methods
v.reverse() # Modifies in place!
print(f"After reverse: {v}")
v.append(5) # Now 3D?
print(f"After append: {v}")Vector: [3, 4]
Magnitude: 5.0
After reverse: [4, 3]
After append: [4, 3, 5]# Composition approach
class Signal:
"""Signal uses composition."""
def __init__(self, data, sample_rate):
self._data = np.array(data)
self.fs = sample_rate
self._filter = None
def __len__(self):
return len(self._data)
def __getitem__(self, idx):
return self._data[idx]
@property
def duration(self):
return len(self._data) / self.fs
def fft(self):
"""Delegate to NumPy."""
return np.fft.fft(self._data)
def resample(self, new_rate):
"""Return new Signal."""
ratio = new_rate / self.fs
new_length = int(len(self._data) * ratio)
new_data = np.interp(
np.linspace(0, len(self._data), new_length),
np.arange(len(self._data)),
self._data
)
return Signal(new_data, new_rate)
# Clean interface
sig = Signal([1, 2, 3, 4], sample_rate=100)
print(f"Duration: {sig.duration}s")
print(f"FFT shape: {sig.fft().shape}")Duration: 0.04s
FFT shape: (4,)Classes and Operator Overloading
Object Creation and Initialization
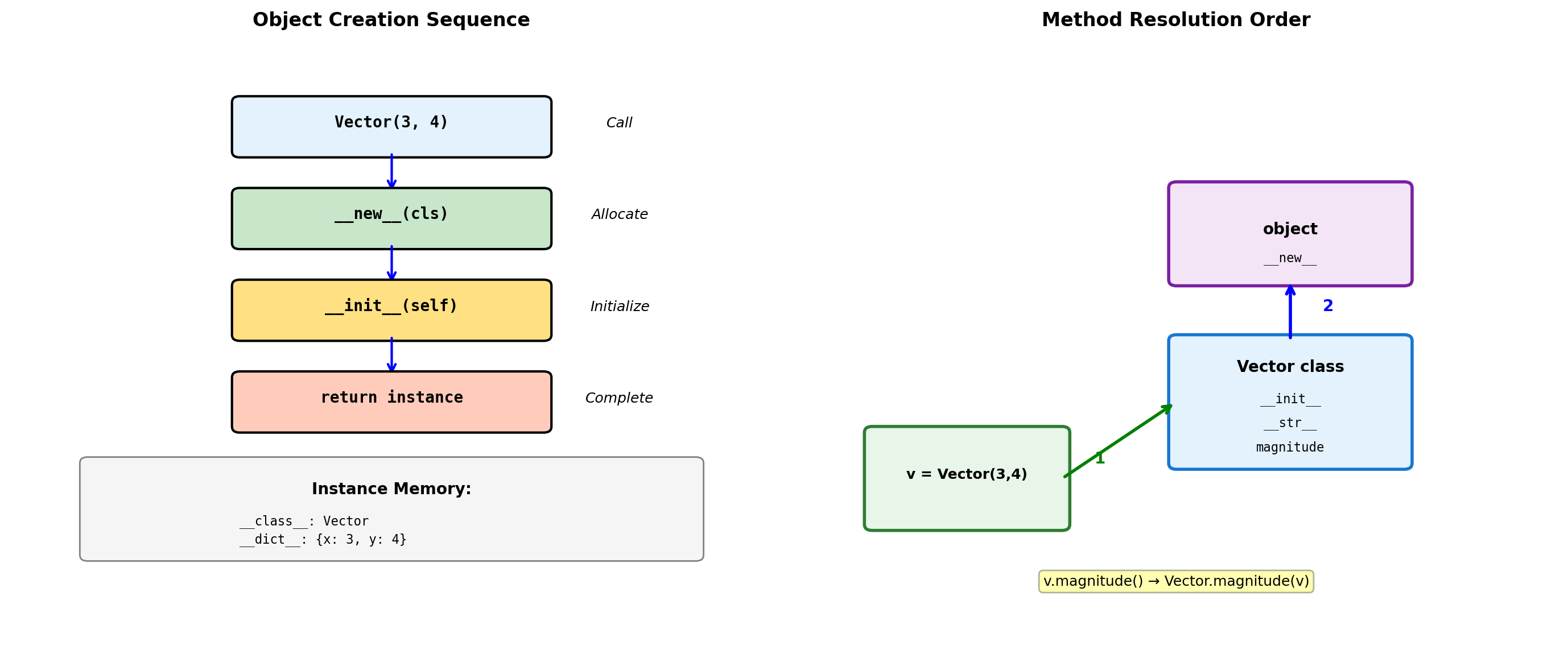
class Vector:
"""2D vector with special methods."""
def __init__(self, x, y):
"""Initialize instance attributes."""
self.x = x
self.y = y
def __repr__(self):
"""Developer representation (for debugging)."""
return f"Vector({self.x}, {self.y})"
def __str__(self):
"""User-friendly string representation."""
return f"<{self.x}, {self.y}>"
def magnitude(self):
"""Compute vector magnitude."""
return (self.x**2 + self.y**2) ** 0.5
# Create instance
v = Vector(3, 4)
# Different string representations
print(f"repr(v): {repr(v)}")
print(f"str(v): {str(v)}")
print(f"Magnitude: {v.magnitude()}")
# Instance internals
print(f"\nInstance dict: {v.__dict__}")
print(f"Class: {v.__class__.__name__}")repr(v): Vector(3, 4)
str(v): <3, 4>
Magnitude: 5.0
Instance dict: {'x': 3, 'y': 4}
Class: Vector# Method resolution demonstration
class Base:
def method(self):
return "Base"
def override_me(self):
return "Base version"
class Derived(Base):
def override_me(self):
return "Derived version"
def method(self):
# Call parent version
parent = super().method()
return f"{parent} → Derived"
d = Derived()
print(f"d.override_me(): {d.override_me()}")
print(f"d.method(): {d.method()}")
# MRO (Method Resolution Order)
print(f"\nMRO: {[cls.__name__ for cls in Derived.__mro__]}")
# Bound vs unbound methods
print(f"\nBound method: {d.method}")
print(f"Unbound: {Derived.method}")
print(f"Same function: {d.method.__func__ is Derived.method}")d.override_me(): Derived version
d.method(): Base → Derived
MRO: ['Derived', 'Base', 'object']
Bound method: <bound method Derived.method of <__main__.Derived object at 0x32fa7f350>>
Unbound: <function Derived.method at 0x3489a3100>
Same function: TrueOperator Overloading for Numerical Types
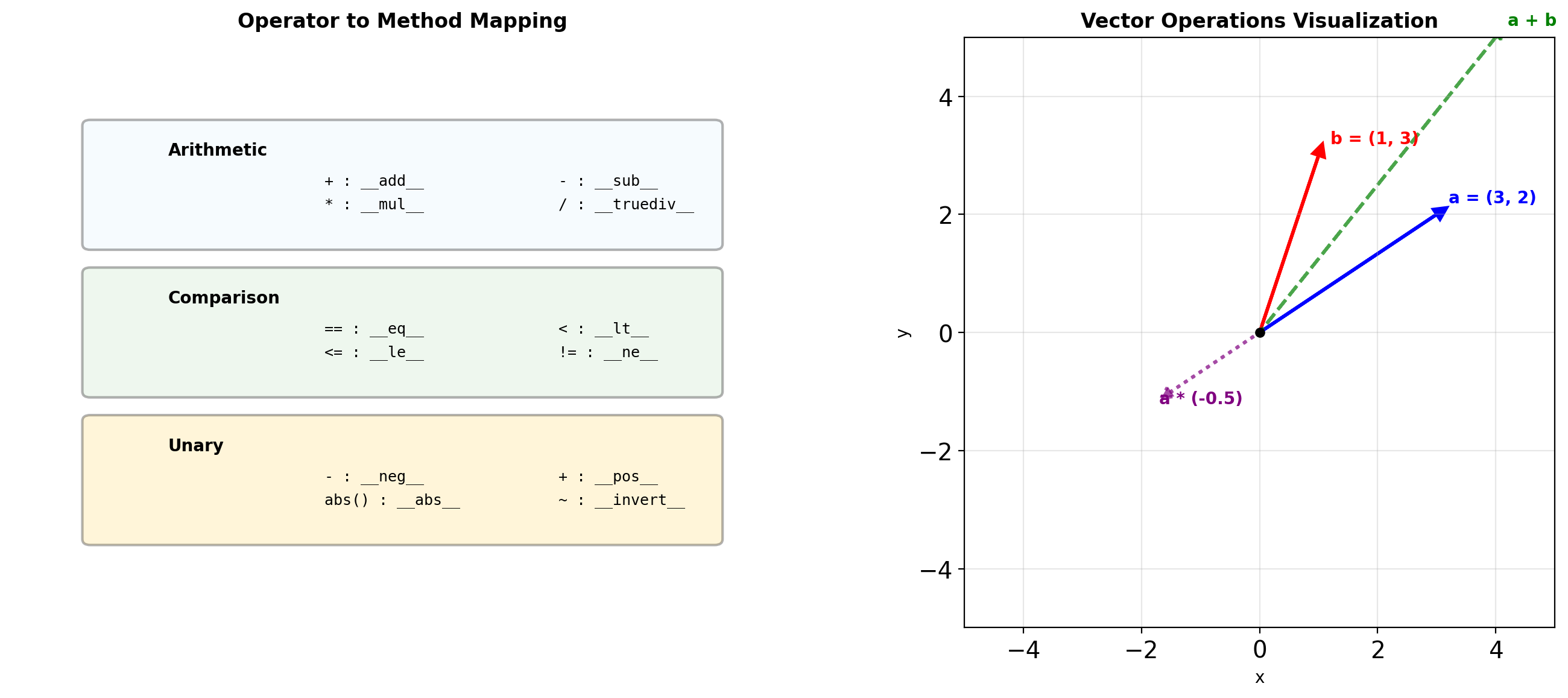
class Vector:
def __init__(self, x, y):
self.x = x
self.y = y
def __repr__(self):
return f"Vector({self.x}, {self.y})"
# Arithmetic operators
def __add__(self, other):
if isinstance(other, Vector):
return Vector(self.x + other.x, self.y + other.y)
return NotImplemented
def __mul__(self, scalar):
if isinstance(scalar, (int, float)):
return Vector(self.x * scalar, self.y * scalar)
return NotImplemented
def __rmul__(self, scalar):
"""Right multiplication: scalar * vector"""
return self.__mul__(scalar)
def __neg__(self):
return Vector(-self.x, -self.y)
def __abs__(self):
return (self.x**2 + self.y**2) ** 0.5
# Comparison operators
def __eq__(self, other):
if not isinstance(other, Vector):
return False
return self.x == other.x and self.y == other.y
def __lt__(self, other):
"""Compare by magnitude."""
return abs(self) < abs(other)
# Usage
a = Vector(3, 4)
b = Vector(1, 2)
print(f"a = {a}")
print(f"b = {b}")
print(f"a + b = {a + b}")
print(f"2 * a = {2 * a}")
print(f"-a = {-a}")
print(f"|a| = {abs(a)}")
print(f"a == b: {a == b}")
print(f"a > b: {a > b}")a = Vector(3, 4)
b = Vector(1, 2)
a + b = Vector(4, 6)
2 * a = Vector(6, 8)
-a = Vector(-3, -4)
|a| = 5.0
a == b: False
a > b: True# In-place operators
class Matrix:
def __init__(self, data):
self.data = np.array(data, dtype=float)
def __repr__(self):
return f"Matrix({self.data.tolist()})"
def __iadd__(self, other):
"""In-place addition: m += other"""
if isinstance(other, Matrix):
self.data += other.data
elif isinstance(other, (int, float)):
self.data += other
else:
return NotImplemented
return self # Must return self
def __matmul__(self, other):
"""Matrix multiplication: m @ other"""
if isinstance(other, Matrix):
return Matrix(self.data @ other.data)
return NotImplemented
def __getitem__(self, key):
"""Indexing: m[i, j]"""
return self.data[key]
def __setitem__(self, key, value):
"""Assignment: m[i, j] = value"""
self.data[key] = value
# Usage
m1 = Matrix([[1, 2], [3, 4]])
m2 = Matrix([[5, 6], [7, 8]])
print(f"m1 = {m1}")
print(f"m2 = {m2}")
print(f"m1 @ m2 = {m1 @ m2}")
print(f"m1[0, 1] = {m1[0, 1]}")
m1 += 10
print(f"After m1 += 10: {m1}")m1 = Matrix([[1.0, 2.0], [3.0, 4.0]])
m2 = Matrix([[5.0, 6.0], [7.0, 8.0]])
m1 @ m2 = Matrix([[19.0, 22.0], [43.0, 50.0]])
m1[0, 1] = 2.0
After m1 += 10: Matrix([[11.0, 12.0], [13.0, 14.0]])Properties and Descriptors
class Temperature:
"""Temperature with Celsius/Fahrenheit properties."""
def __init__(self, celsius=0):
self._celsius = celsius
@property
def celsius(self):
"""Getter for Celsius."""
return self._celsius
@celsius.setter
def celsius(self, value):
"""Setter with validation."""
if value < -273.15:
raise ValueError(f"Temperature below absolute zero")
self._celsius = value
@property
def fahrenheit(self):
"""Computed Fahrenheit property."""
return self._celsius * 9/5 + 32
@fahrenheit.setter
def fahrenheit(self, value):
"""Set via Fahrenheit."""
self.celsius = (value - 32) * 5/9
@property
def kelvin(self):
"""Read-only Kelvin property."""
return self._celsius + 273.15
# Usage
temp = Temperature(25)
print(f"Celsius: {temp.celsius}°C")
print(f"Fahrenheit: {temp.fahrenheit}°F")
print(f"Kelvin: {temp.kelvin}K")
temp.fahrenheit = 86
print(f"\nAfter setting 86°F:")
print(f"Celsius: {temp.celsius}°C")
try:
temp.celsius = -300
except ValueError as e:
print(f"\nValidation error: {e}")Celsius: 25°C
Fahrenheit: 77.0°F
Kelvin: 298.15K
After setting 86°F:
Celsius: 30.0°C
Validation error: Temperature below absolute zeroWhen to use properties:
- Computed values derived from other attributes
- Validation on attribute assignment
- Converting between representations (e.g., Celsius/Fahrenheit)
- Read-only attributes that shouldn’t be modified
Property mechanics:
- Getter: Called on
obj.attraccess - Setter: Called on
obj.attr = valueassignment - Deleter: Called on
del obj.attr - Properties are descriptors under the hood
Class vs Instance Attributes
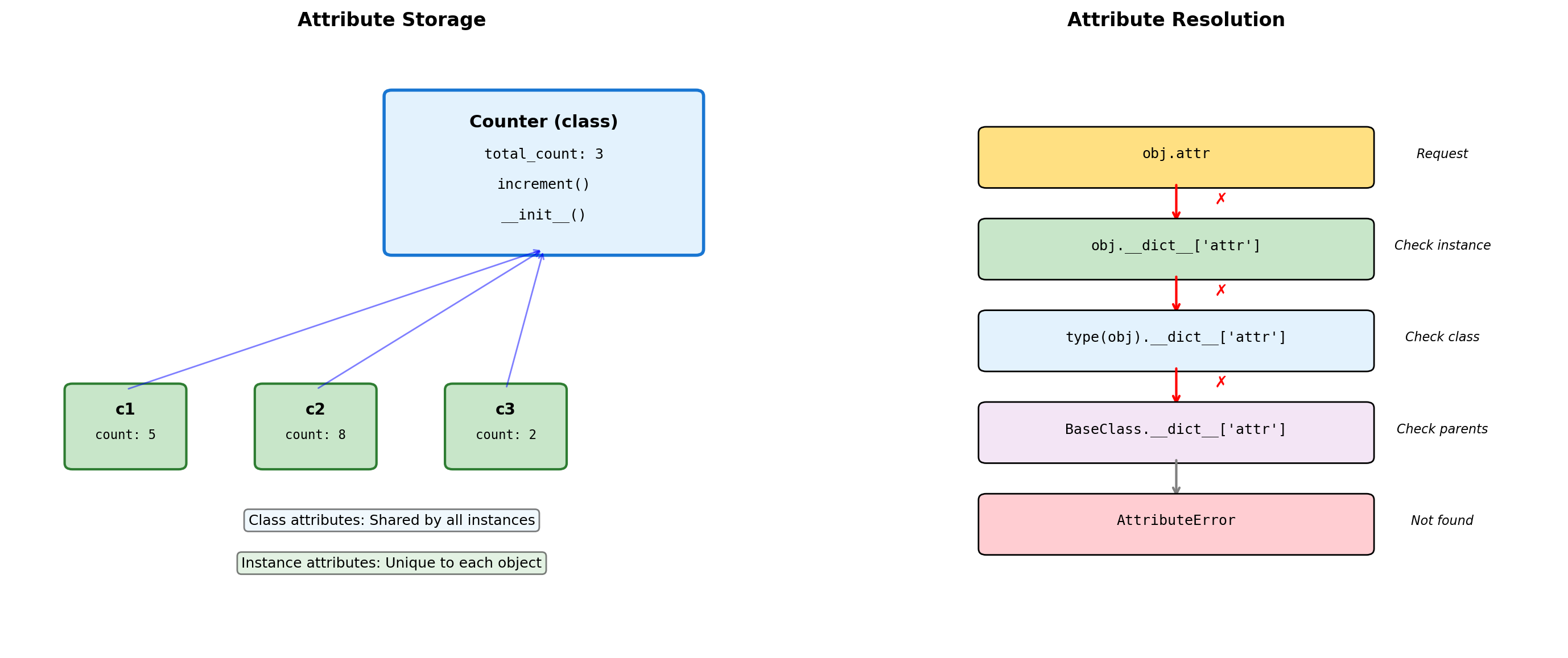
class Counter:
"""Demonstrates class vs instance attributes."""
# Class attribute (shared)
total_instances = 0
default_step = 1
def __init__(self, initial=0):
# Instance attributes (unique)
self.count = initial
Counter.total_instances += 1
def increment(self, step=None):
# Use class default if not specified
if step is None:
step = self.default_step
self.count += step
@classmethod
def get_total(cls):
"""Class method accesses class attributes."""
return cls.total_instances
@staticmethod
def validate_step(step):
"""Static method - no access to instance or class."""
return step > 0
# Create instances
c1 = Counter()
c2 = Counter(10)
c3 = Counter(20)
print(f"Total instances: {Counter.total_instances}")
print(f"c1.count: {c1.count}")
print(f"c2.count: {c2.count}")
# Modify class attribute
Counter.default_step = 5
c1.increment()
c2.increment()
print(f"\nAfter increment with step=5:")
print(f"c1.count: {c1.count}")
print(f"c2.count: {c2.count}")
# Instance shadows class attribute
c1.default_step = 10
print(f"\nc1.default_step: {c1.default_step}")
print(f"c2.default_step: {c2.default_step}")Total instances: 3
c1.count: 0
c2.count: 10
After increment with step=5:
c1.count: 5
c2.count: 15
c1.default_step: 10
c2.default_step: 5Class vs instance attributes:
- Class attributes: Shared by all instances, defined at class level
- Instance attributes: Unique to each object, defined in
__init__ - Instance attributes shadow class attributes of the same name
Method types:
- Instance methods:
selfas first argument, access instance state - Class methods (
@classmethod):clsas first argument, access class state - Static methods (
@staticmethod): No implicit argument, utility functions
Common patterns:
- Class-level defaults modified per-instance
- Instance counters via class attributes
- Factory methods via
@classmethod
Abstract Base Classes and Protocols
from abc import ABC, abstractmethod
import math
class Shape(ABC):
"""Abstract base class for shapes."""
@abstractmethod
def area(self):
"""Must be implemented by subclasses."""
pass
@abstractmethod
def perimeter(self):
"""Must be implemented by subclasses."""
pass
def describe(self):
"""Concrete method using abstract methods."""
return f"Area: {self.area():.2f}, Perimeter: {self.perimeter():.2f}"
class Circle(Shape):
def __init__(self, radius):
self.radius = radius
def area(self):
return math.pi * self.radius ** 2
def perimeter(self):
return 2 * math.pi * self.radius
class Rectangle(Shape):
def __init__(self, width, height):
self.width = width
self.height = height
def area(self):
return self.width * self.height
def perimeter(self):
return 2 * (self.width + self.height)
# Cannot instantiate ABC
try:
shape = Shape() # Error!
except TypeError as e:
print(f"Error: {e}")
# Concrete classes work
circle = Circle(5)
rect = Rectangle(3, 4)
print(f"\nCircle: {circle.describe()}")
print(f"Rectangle: {rect.describe()}")
# Check inheritance
print(f"\nisinstance(circle, Shape): {isinstance(circle, Shape)}")Error: Can't instantiate abstract class Shape with abstract methods area, perimeter
Circle: Area: 78.54, Perimeter: 31.42
Rectangle: Area: 12.00, Perimeter: 14.00
isinstance(circle, Shape): TrueWhen to use ABCs:
- Defining interfaces that must be implemented
- Template Method pattern (concrete methods calling abstract ones)
- Enforcing contracts in a class hierarchy
- When you want
isinstance()checks against the interface
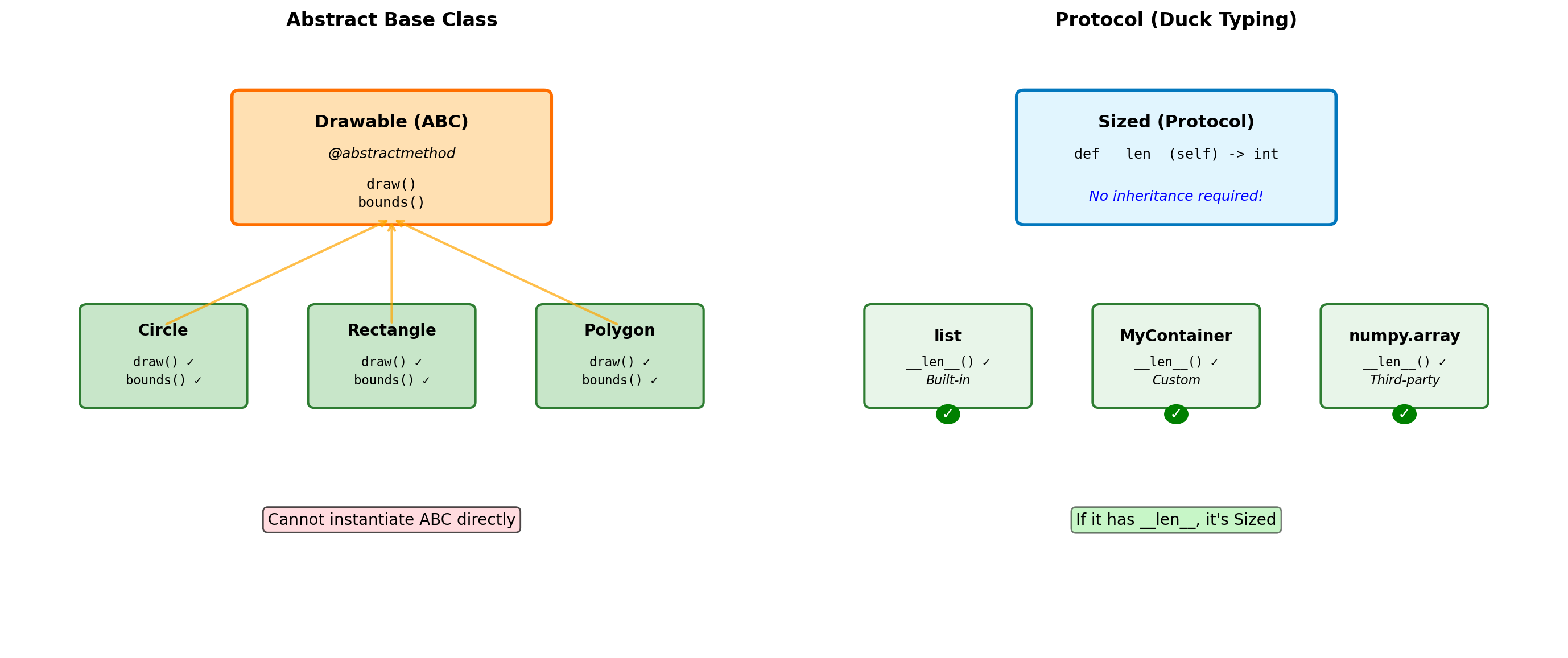
ABC vs Duck Typing:
- ABCs: Explicit contracts, errors at instantiation time
- Duck typing: Implicit contracts, errors at call time
- Python prefers duck typing, but ABCs useful for frameworks
Built-in ABCs (collections.abc):
Iterable,Iterator,SequenceMapping,MutableMappingCallable,Hashable
Dataclasses for Numerical Structures
from dataclasses import dataclass, field
from typing import List
import numpy as np
@dataclass
class DataPoint:
"""Simple data container."""
x: float
y: float
label: str = "unlabeled"
metadata: dict = field(default_factory=dict)
def distance_to(self, other):
"""Euclidean distance."""
return ((self.x - other.x)**2 +
(self.y - other.y)**2) ** 0.5
@dataclass(frozen=True)
class ImmutableVector:
"""Frozen dataclass - hashable."""
x: float
y: float
z: float
def magnitude(self):
return (self.x**2 + self.y**2 + self.z**2) ** 0.5
def __add__(self, other):
"""Return new vector (immutable)."""
return ImmutableVector(
self.x + other.x,
self.y + other.y,
self.z + other.z
)
# Usage
p1 = DataPoint(3, 4)
p2 = DataPoint(6, 8, "target")
print(f"p1: {p1}")
print(f"p2: {p2}")
print(f"Distance: {p1.distance_to(p2):.2f}")
# Frozen vector
v1 = ImmutableVector(1, 2, 3)
v2 = ImmutableVector(4, 5, 6)
v3 = v1 + v2
print(f"\nv1 + v2 = {v3}")
print(f"Hashable: {hash(v1)}")
# Can use as dict key
vector_dict = {v1: "first", v2: "second"}p1: DataPoint(x=3, y=4, label='unlabeled', metadata={})
p2: DataPoint(x=6, y=8, label='target', metadata={})
Distance: 5.00
v1 + v2 = ImmutableVector(x=5, y=7, z=9)
Hashable: 529344067295497451@dataclass(order=True)
class Measurement:
"""Sortable measurement with validation."""
timestamp: float = field(compare=True)
value: float = field(compare=False)
sensor_id: str = field(default="unknown", compare=False)
def __post_init__(self):
"""Validation after initialization."""
if self.value < 0:
raise ValueError(f"Negative value: {self.value}")
if self.timestamp < 0:
raise ValueError(f"Invalid timestamp: {self.timestamp}")
# Sorting by timestamp
measurements = [
Measurement(100.5, 23.4, "A1"),
Measurement(99.2, 25.1, "A2"),
Measurement(101.3, 22.8, "A1"),
]
sorted_measurements = sorted(measurements)
print("Sorted by timestamp:")
for m in sorted_measurements:
print(f" t={m.timestamp}: {m.value}")
# Performance comparison
from dataclasses import dataclass
import sys
@dataclass(slots=True)
class SlottedPoint:
x: float
y: float
@dataclass
class RegularPoint:
x: float
y: float
sp = SlottedPoint(1, 2)
rp = RegularPoint(1, 2)
print(f"\nMemory usage:")
print(f" With slots: {sys.getsizeof(sp)} bytes")
print(f" Regular: {sys.getsizeof(rp) + sys.getsizeof(rp.__dict__)} bytes")Sorted by timestamp:
t=99.2: 25.1
t=100.5: 23.4
t=101.3: 22.8
Memory usage:
With slots: 48 bytes
Regular: 352 bytesNumPy Arrays
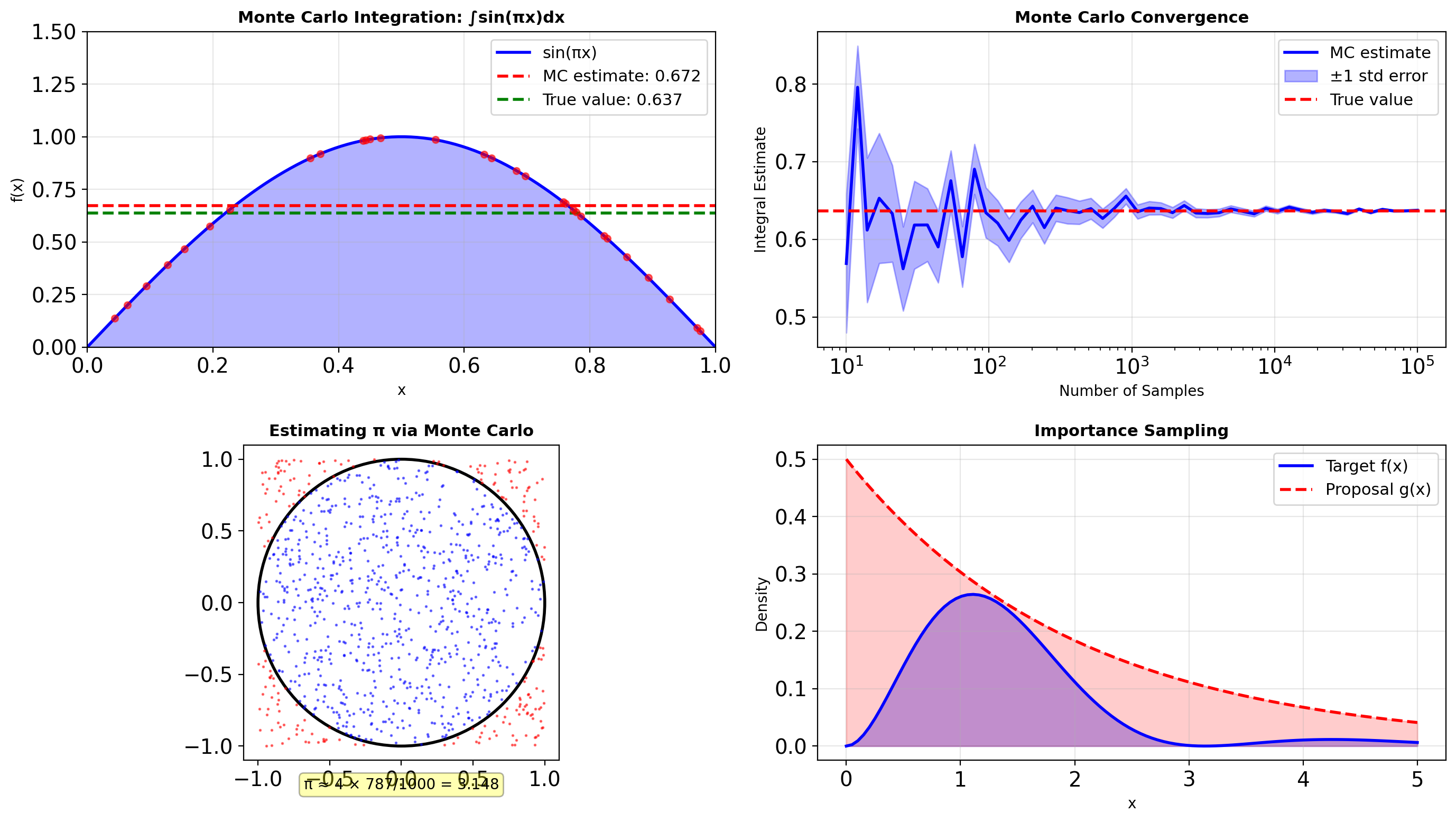
Why NumPy Exists: Python’s Performance Wall
NumPy solves Python’s fundamental limitation: every operation triggers expensive interpreter overhead.
import numpy as np
import timeit
# Demonstrate the performance difference
def python_add(list1, list2):
"""Pure Python element-wise addition."""
result = []
for i in range(len(list1)):
result.append(list1[i] + list2[i])
return result
def numpy_add(arr1, arr2):
"""NumPy vectorized addition."""
return arr1 + arr2
# Test data
size = 100000
py_list1 = list(range(size))
py_list2 = list(range(size, size*2))
np_arr1 = np.array(py_list1)
np_arr2 = np.array(py_list2)
# Benchmark
t_python = timeit.timeit(
lambda: python_add(py_list1, py_list2),
number=10
)
t_numpy = timeit.timeit(
lambda: numpy_add(np_arr1, np_arr2),
number=10
)
print(f"Adding {size:,} numbers (10 iterations):")
print(f" Python lists: {t_python:.3f}s")
print(f" NumPy arrays: {t_numpy:.3f}s")
print(f" Speedup: {t_python/t_numpy:.0f}x")
# Show function call overhead
python_ops = size * 4 # loop, 2 indexes, 1 addition per iteration
numpy_ops = 1 # single function call
print(f"\nPython operations: {python_ops:,}")
print(f"NumPy operations: {numpy_ops}")
print(f"Overhead reduction: {python_ops/numpy_ops:.0f}x")Adding 100,000 numbers (10 iterations):
Python lists: 0.024s
NumPy arrays: 0.000s
Speedup: 61x
Python operations: 400,000
NumPy operations: 1
Overhead reduction: 400000xThe NumPy Solution:
- Homogeneous data - All elements same type, enabling compact storage
- Contiguous memory - Cache-friendly access patterns
- Vectorized operations - Single Python call processes entire arrays
- C implementation - Inner loops run at machine speed
Cost of flexibility:
- Python lists can mix types, NumPy arrays cannot
- Dynamic resizing is expensive in NumPy
- Small arrays may be slower due to overhead
When NumPy wins:
- Numerical computations on large datasets
- Element-wise operations
- Mathematical functions (sin, cos, exp)
- Linear algebra operations
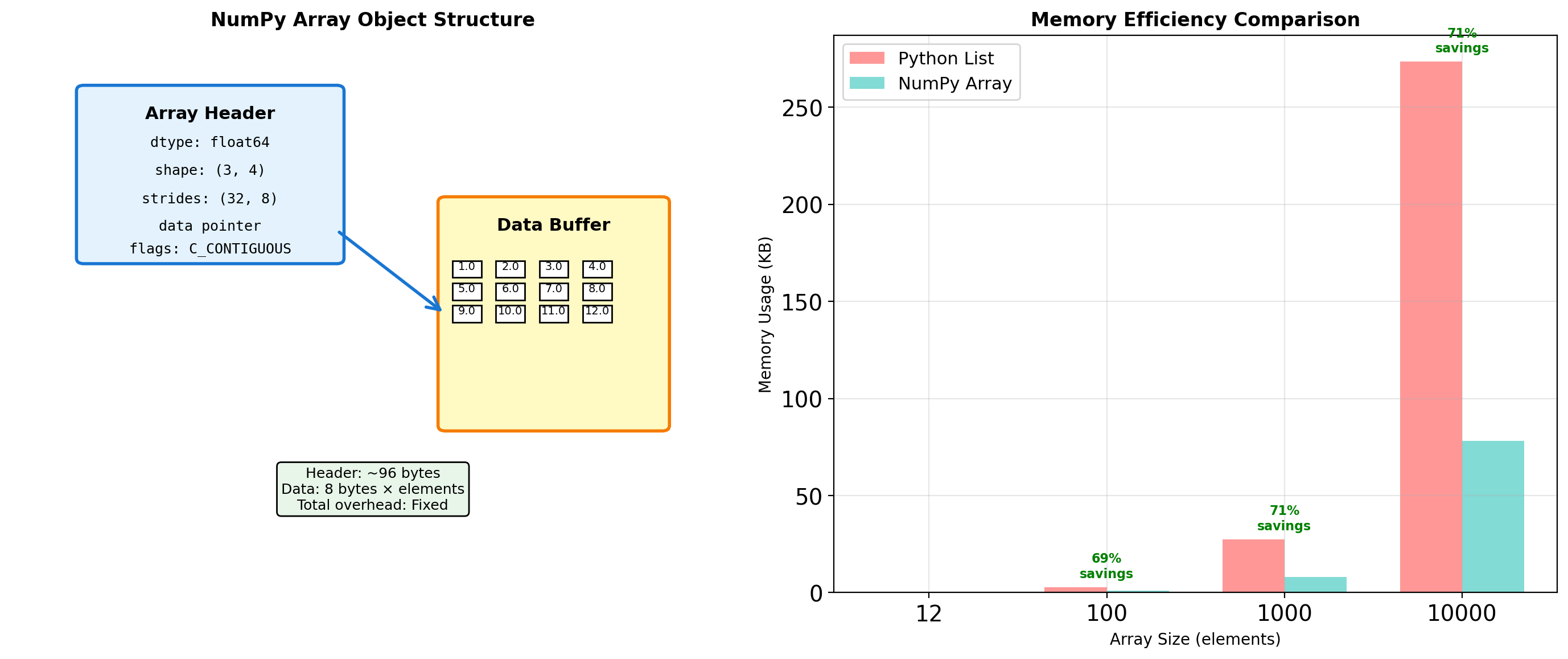
Array Object Internals: More Than Just Data
NumPy arrays are sophisticated objects that separate metadata from data, enabling powerful features like views and broadcasting.
import numpy as np
import sys
# Examine array internals
arr = np.arange(12, dtype=np.float64).reshape(3, 4)
print("Array structure analysis:")
print(f" Array object size: {sys.getsizeof(arr)} bytes")
print(f" Data buffer size: {arr.nbytes} bytes")
print(f" Shape: {arr.shape}")
print(f" Strides: {arr.strides}") # Bytes to next element in each dimension
print(f" Data type: {arr.dtype}")
print(f" Item size: {arr.itemsize} bytes")
# Memory layout inspection
print(f"\nMemory layout:")
print(f" C-contiguous: {arr.flags['C_CONTIGUOUS']}")
print(f" F-contiguous: {arr.flags['F_CONTIGUOUS']}")
print(f" Owns data: {arr.flags['OWNDATA']}")
# Compare with Python list
py_list = arr.tolist()
print(f"\nMemory comparison for 12 elements:")
print(f" NumPy array: {sys.getsizeof(arr) + arr.nbytes} bytes total")
print(f" Python list: {sys.getsizeof(py_list)} bytes (list)")
# Calculate Python list element overhead
element_overhead = sum(sys.getsizeof(x) for row in py_list for x in row)
print(f" Python objects: {element_overhead} bytes (elements)")
print(f" Python total: {sys.getsizeof(py_list) + element_overhead} bytes")
# Show memory addressing
print(f"\nMemory addressing:")
print(f" Base address: {arr.__array_interface__['data'][0]:#x}")
print(f" Element [0,0] offset: 0 bytes")
print(f" Element [0,1] offset: {arr.strides[1]} bytes")
print(f" Element [1,0] offset: {arr.strides[0]} bytes")
# Demonstrate stride calculation
row, col = 1, 2
offset = row * arr.strides[0] + col * arr.strides[1]
print(f" Element [1,2] offset: {offset} bytes → value {arr[1,2]}")Array structure analysis:
Array object size: 128 bytes
Data buffer size: 96 bytes
Shape: (3, 4)
Strides: (32, 8)
Data type: float64
Item size: 8 bytes
Memory layout:
C-contiguous: True
F-contiguous: False
Owns data: False
Memory comparison for 12 elements:
NumPy array: 224 bytes total
Python list: 80 bytes (list)
Python objects: 288 bytes (elements)
Python total: 368 bytes
Memory addressing:
Base address: 0x1225bbe60
Element [0,0] offset: 0 bytes
Element [0,1] offset: 8 bytes
Element [1,0] offset: 32 bytes
Element [1,2] offset: 48 bytes → value 6.0Array metadata enables:
- Reshaping without copying - Same data, different view
- Slicing creates views - No memory duplication
- Broadcasting - Operations on different-shaped arrays
- Memory mapping - Work with files larger than RAM
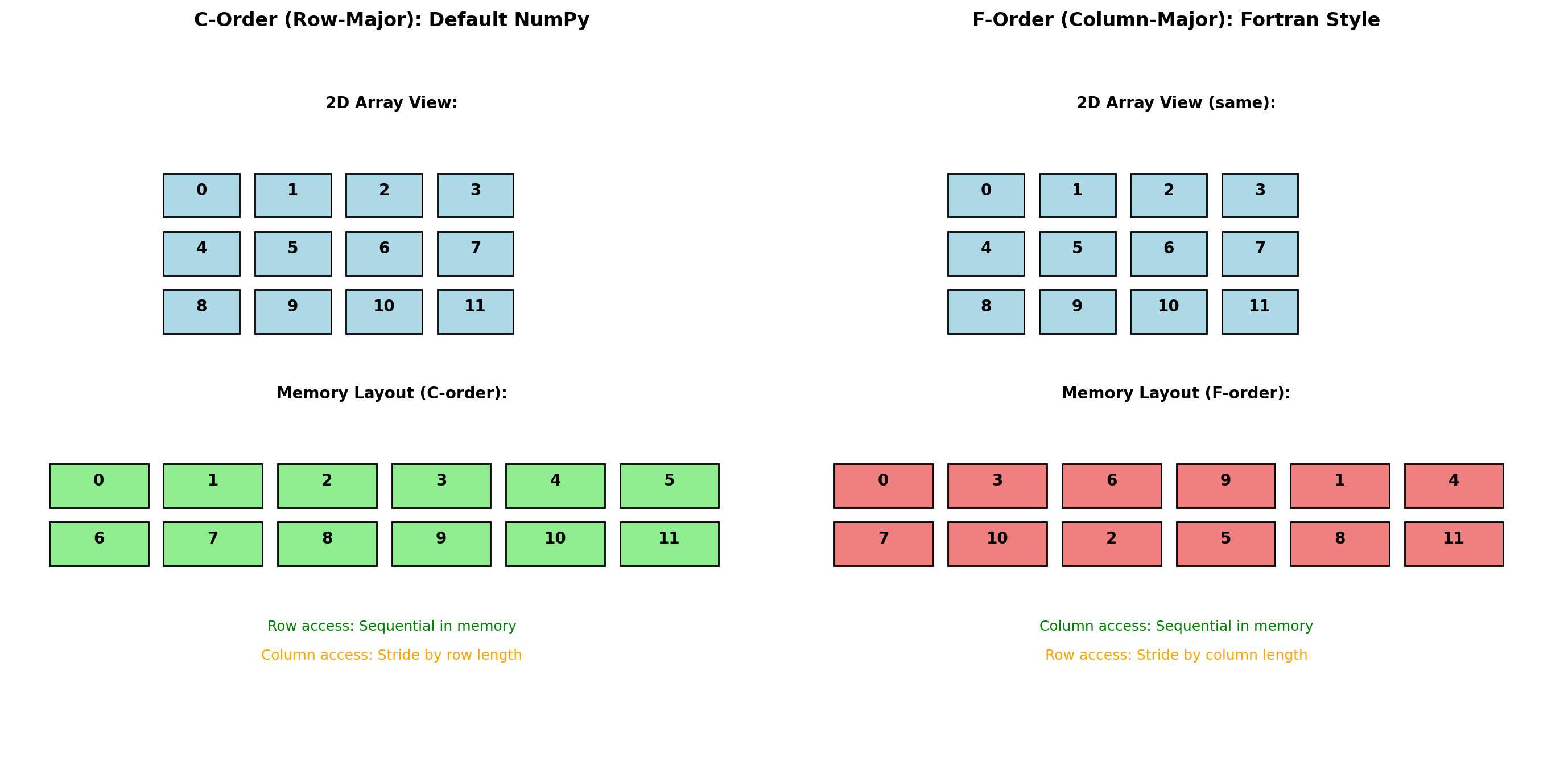
Memory Layout: Row-Major vs Column-Major
Array element ordering in memory affects performance significantly due to CPU cache behavior.
import numpy as np
import timeit
# Create arrays with different memory layouts
size = 1000
c_array = np.random.rand(size, size) # C-order (default)
f_array = np.asfortranarray(c_array) # F-order copy
print("Memory layout comparison:")
print(f"C-order shape: {c_array.shape}, strides: {c_array.strides}")
print(f"F-order shape: {f_array.shape}, strides: {f_array.strides}")
print(f"C-order flags: C={c_array.flags.c_contiguous}, F={c_array.flags.f_contiguous}")
print(f"F-order flags: C={f_array.flags.c_contiguous}, F={f_array.flags.f_contiguous}")
# Row access performance (C-order wins)
def sum_rows(arr):
return [np.sum(arr[i, :]) for i in range(100)]
# Column access performance (F-order wins)
def sum_cols(arr):
return [np.sum(arr[:, j]) for j in range(100)]
t_c_rows = timeit.timeit(lambda: sum_rows(c_array), number=100)
t_f_rows = timeit.timeit(lambda: sum_rows(f_array), number=100)
t_c_cols = timeit.timeit(lambda: sum_cols(c_array), number=100)
t_f_cols = timeit.timeit(lambda: sum_cols(f_array), number=100)
print(f"\nRow access performance (100 iterations):")
print(f" C-order: {t_c_rows:.3f}s")
print(f" F-order: {t_f_rows:.3f}s ({t_f_rows/t_c_rows:.1f}x slower)")
print(f"\nColumn access performance (100 iterations):")
print(f" C-order: {t_c_cols:.3f}s")
print(f" F-order: {t_f_cols:.3f}s ({t_c_cols/t_f_cols:.1f}x faster)")Memory layout comparison:
C-order shape: (1000, 1000), strides: (8000, 8)
F-order shape: (1000, 1000), strides: (8, 8000)
C-order flags: C=True, F=False
F-order flags: C=False, F=True
Row access performance (100 iterations):
C-order: 0.015s
F-order: 0.017s (1.2x slower)
Column access performance (100 iterations):
C-order: 0.017s
F-order: 0.015s (1.1x faster)Memory layout matters because:
- CPU cache lines - Fetch 64-byte chunks from RAM
- Spatial locality - Adjacent memory access is faster
- Prefetching - CPU predicts sequential access patterns
C-order (row-major):
- Default in NumPy, C, Python
- Rows stored contiguously
- Better for row operations
F-order (column-major):
- Default in Fortran, MATLAB, R
- Columns stored contiguously
- Better for column operations
- Required by some BLAS routines
Performance implications:
- Cache misses can cause 100× slowdowns
- Matrix algorithms should match layout
- Transpose operations may change layout
Views vs Copies: Memory Management Semantics
NumPy operations can either create views (sharing data) or copies (duplicating data). Understanding the difference prevents bugs and optimizes memory usage.
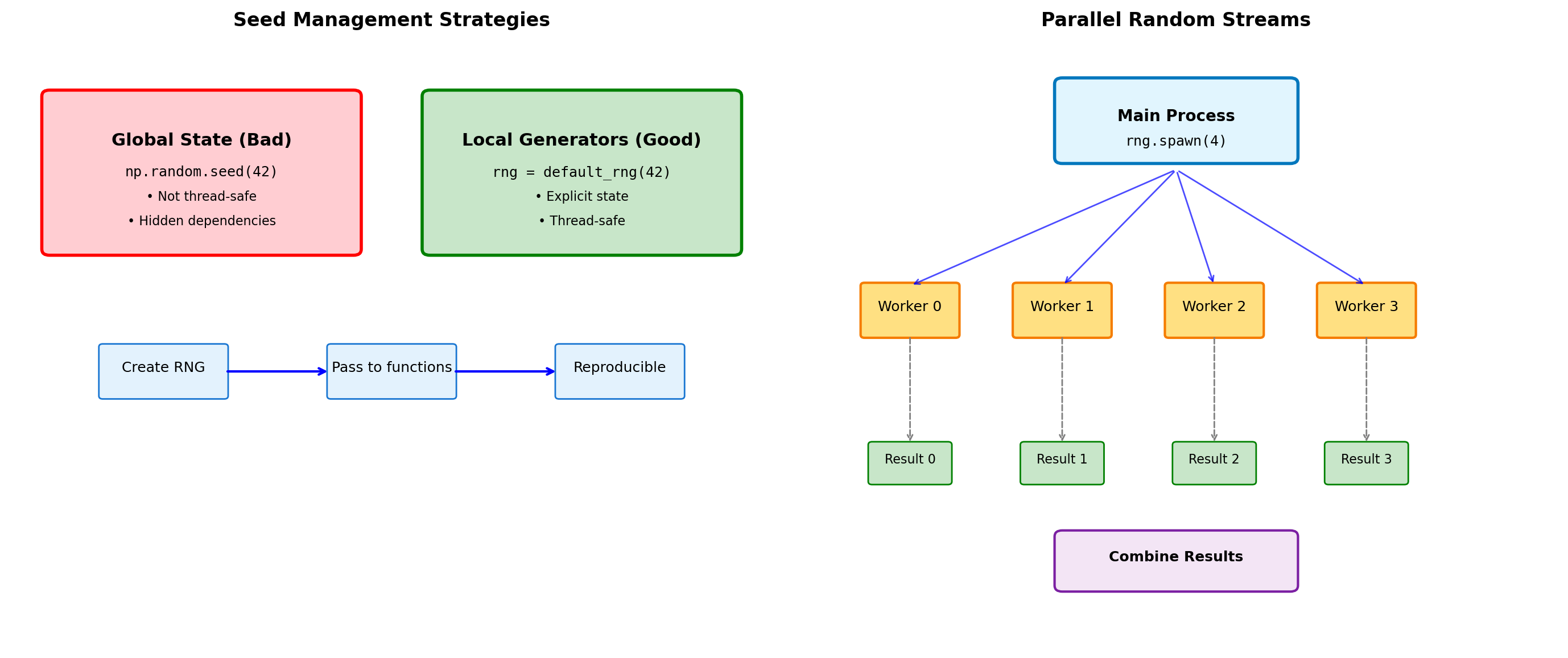
import numpy as np
# Create original array
original = np.arange(12).reshape(3, 4)
print("Original array:")
print(original)
# View operations (share data)
view_reshaped = original.reshape(4, 3)
view_slice = original[1:, :]
view_transpose = original.T
print(f"\nView operations (share data):")
print(f" original.base is None: {original.base is None}")
print(f" view_reshaped.base is original: {view_reshaped.base is original}")
print(f" view_slice.base is original: {view_slice.base is original}")
print(f" view_transpose.base is original: {view_transpose.base is original}")
# Test sharing - modify through view
original[0, 0] = 999
print(f"\nAfter setting original[0,0] = 999:")
print(f" original[0,0] = {original[0,0]}")
print(f" view_reshaped[0,0] = {view_reshaped[0,0]}") # Same memory!
# Copy operations (independent data)
copy_array = original.copy()
copy_flatten = original.flatten() # Unlike ravel(), always copies
print(f"\nCopy operations (independent data):")
print(f" copy_array.base is None: {copy_array.base is None}")
print(f" copy_flatten.base is None: {copy_flatten.base is None}")
# Test independence
original[1, 1] = 888
print(f"\nAfter setting original[1,1] = 888:")
print(f" original[1,1] = {original[1,1]}")
print(f" copy_array[1,1] = {copy_array[1,1]}") # Independent!
# Memory usage comparison
import sys
print(f"\nMemory usage:")
print(f" Original: {original.nbytes} bytes")
print(f" View: {view_reshaped.nbytes} bytes data (shares with original)")
print(f" Copy: {copy_array.nbytes} bytes (independent)")
print(f" Total with view: ~{original.nbytes} bytes")
print(f" Total with copy: ~{original.nbytes + copy_array.nbytes} bytes")
# Dangerous view scenario
def demonstrate_view_trap():
"""Common mistake with views."""
data = np.arange(10)
subset = data[::2] # Every other element (view)
# Modify original
data.fill(0)
return subset # Returns modified data!
result = demonstrate_view_trap()
print(f"\nView trap result: {result}") # All zeros, not original values!Original array:
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]
View operations (share data):
original.base is None: False
view_reshaped.base is original: False
view_slice.base is original: False
view_transpose.base is original: False
After setting original[0,0] = 999:
original[0,0] = 999
view_reshaped[0,0] = 999
Copy operations (independent data):
copy_array.base is None: True
copy_flatten.base is None: True
After setting original[1,1] = 888:
original[1,1] = 888
copy_array[1,1] = 5
Memory usage:
Original: 96 bytes
View: 96 bytes data (shares with original)
Copy: 96 bytes (independent)
Total with view: ~96 bytes
Total with copy: ~192 bytes
View trap result: [0 0 0 0 0]View operations (share data):
- Slicing:
arr[start:stop] - Reshaping:
arr.reshape() - Transposing:
arr.T - Index arrays with step:
arr[::2]
Copy operations (new data):
- Explicit copy:
arr.copy() - Fancy indexing:
arr[[1,3,5]] - Boolean indexing:
arr[arr > 0] - Some functions:
flatten(),ravel()(conditionally)
Broadcasting: Operations on Different-Shaped Arrays
Broadcasting enables operations between arrays of different shapes without explicit loops or memory duplication.
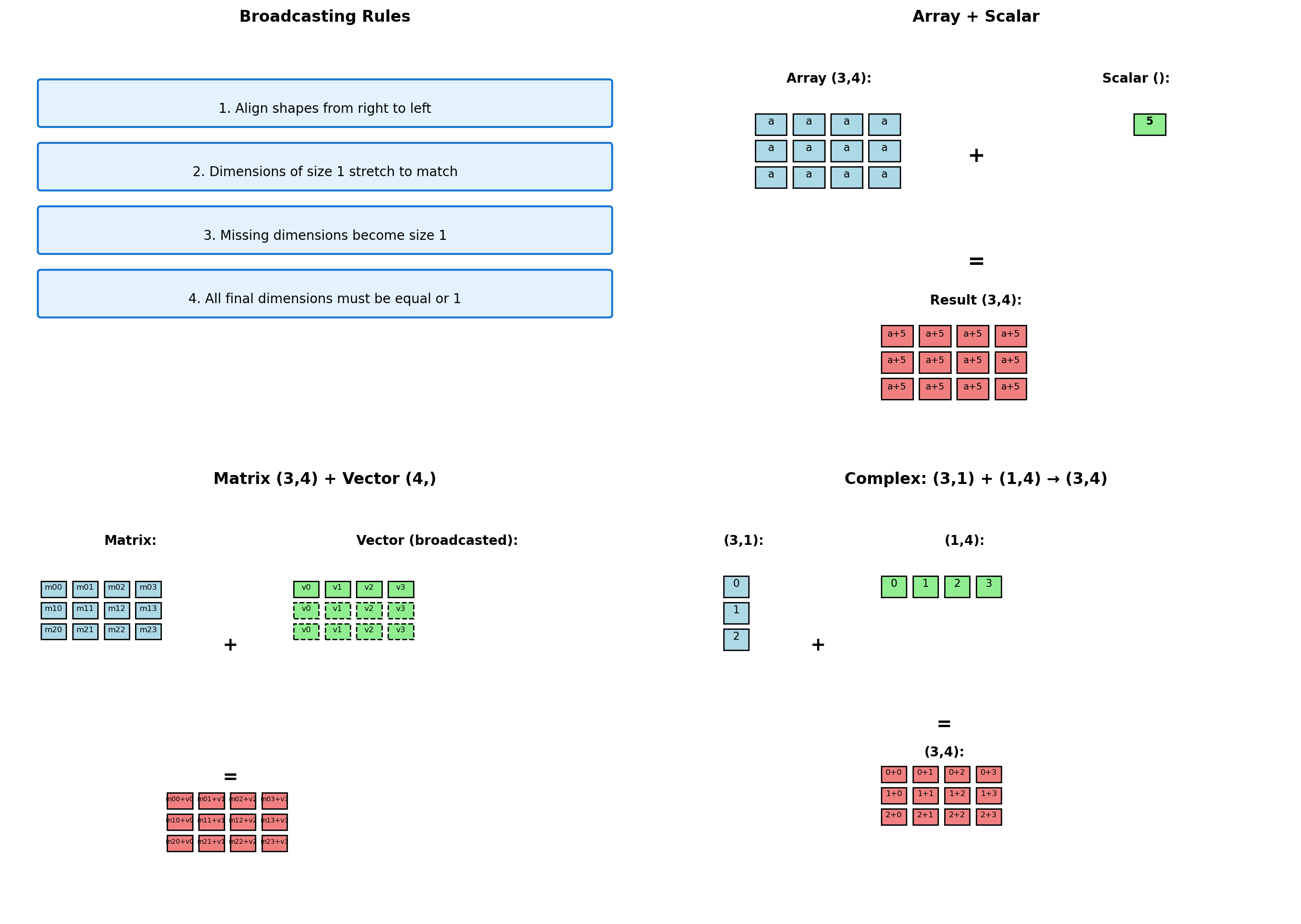
import numpy as np
# Broadcasting examples with shape analysis
def show_broadcast(a, b, operation_name):
"""Demonstrate broadcasting between two arrays."""
print(f"\n{operation_name}:")
print(f" Array A shape: {a.shape}")
# Handle scalar case
if np.isscalar(b):
print(f" Array B: scalar ({b})")
b_bytes = 8 # Approximate scalar size
else:
print(f" Array B shape: {b.shape}")
b_bytes = b.nbytes
try:
result = a + b
print(f" Result shape: {result.shape}")
print(f" Memory usage: A={a.nbytes}B, B={b_bytes}B, Result={result.nbytes}B")
return result
except ValueError as e:
print(f" Error: {e}")
return None
# Example 1: Scalar broadcasting
a1 = np.array([[1, 2, 3], [4, 5, 6]])
b1 = 10
result1 = show_broadcast(a1, b1, "Matrix + Scalar")
# Example 2: Vector to matrix
a2 = np.array([[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12]])
b2 = np.array([100, 200, 300, 400])
result2 = show_broadcast(a2, b2, "Matrix + Row Vector")
# Example 3: Column vector to matrix
a3 = a2 # Same matrix
b3 = np.array([[10], [20], [30]]) # Column vector
result3 = show_broadcast(a3, b3, "Matrix + Column Vector")
# Example 4: Two vectors creating matrix
a4 = np.array([[1], [2], [3]]) # (3,1)
b4 = np.array([10, 20, 30, 40]) # (4,)
result4 = show_broadcast(a4, b4, "Column Vector + Row Vector")
# Example 5: Incompatible shapes
a5 = np.array([[1, 2, 3], [4, 5, 6]]) # (2,3)
b5 = np.array([1, 2]) # (2,)
result5 = show_broadcast(a5, b5, "Incompatible Shapes")
# Memory efficiency demonstration
print(f"\nMemory efficiency:")
large_matrix = np.random.rand(1000, 1000)
small_vector = np.random.rand(1000)
# Without broadcasting (manual)
manual_result = np.zeros_like(large_matrix)
for i in range(1000):
manual_result[i, :] = large_matrix[i, :] + small_vector
# With broadcasting
broadcast_result = large_matrix + small_vector
print(f" Large matrix: {large_matrix.nbytes / 1024**2:.1f} MB")
print(f" Small vector: {small_vector.nbytes / 1024:.1f} KB")
print(f" Broadcasting creates no intermediate arrays")
print(f" Manual approach would need temporary: {manual_result.nbytes / 1024**2:.1f} MB")
# Performance comparison
import timeit
t_manual = timeit.timeit(lambda: np.array([large_matrix[i, :] + small_vector for i in range(10)]), number=100)
t_broadcast = timeit.timeit(lambda: large_matrix[:10, :] + small_vector, number=100)
print(f"\nPerformance (10 rows, 100 iterations):")
print(f" Manual loop: {t_manual:.3f}s")
print(f" Broadcasting: {t_broadcast:.3f}s ({t_manual/t_broadcast:.0f}x faster)")
Matrix + Scalar:
Array A shape: (2, 3)
Array B: scalar (10)
Result shape: (2, 3)
Memory usage: A=48B, B=8B, Result=48B
Matrix + Row Vector:
Array A shape: (3, 4)
Array B shape: (4,)
Result shape: (3, 4)
Memory usage: A=96B, B=32B, Result=96B
Matrix + Column Vector:
Array A shape: (3, 4)
Array B shape: (3, 1)
Result shape: (3, 4)
Memory usage: A=96B, B=24B, Result=96B
Column Vector + Row Vector:
Array A shape: (3, 1)
Array B shape: (4,)
Result shape: (3, 4)
Memory usage: A=24B, B=32B, Result=96B
Incompatible Shapes:
Array A shape: (2, 3)
Array B shape: (2,)
Error: operands could not be broadcast together with shapes (2,3) (2,)
Memory efficiency:
Large matrix: 7.6 MB
Small vector: 7.8 KB
Broadcasting creates no intermediate arrays
Manual approach would need temporary: 7.6 MB
Performance (10 rows, 100 iterations):
Manual loop: 0.001s
Broadcasting: 0.000s (2x faster)Broadcasting advantages:
- Memory efficient - No intermediate arrays created
- Faster than loops - Vectorized C operations
- Clean syntax - Mathematical notation preserved
- Automatic optimization - NumPy handles alignment
Common broadcasting patterns:
- Matrix operations with row/column vectors
- Applying functions across dimensions
- Statistical operations (normalization, standardization)
- Image processing (filters, transformations)
Vectorization: Moving Loops from Python to C
Vectorization replaces Python loops with single operations on entire arrays, dramatically improving performance.
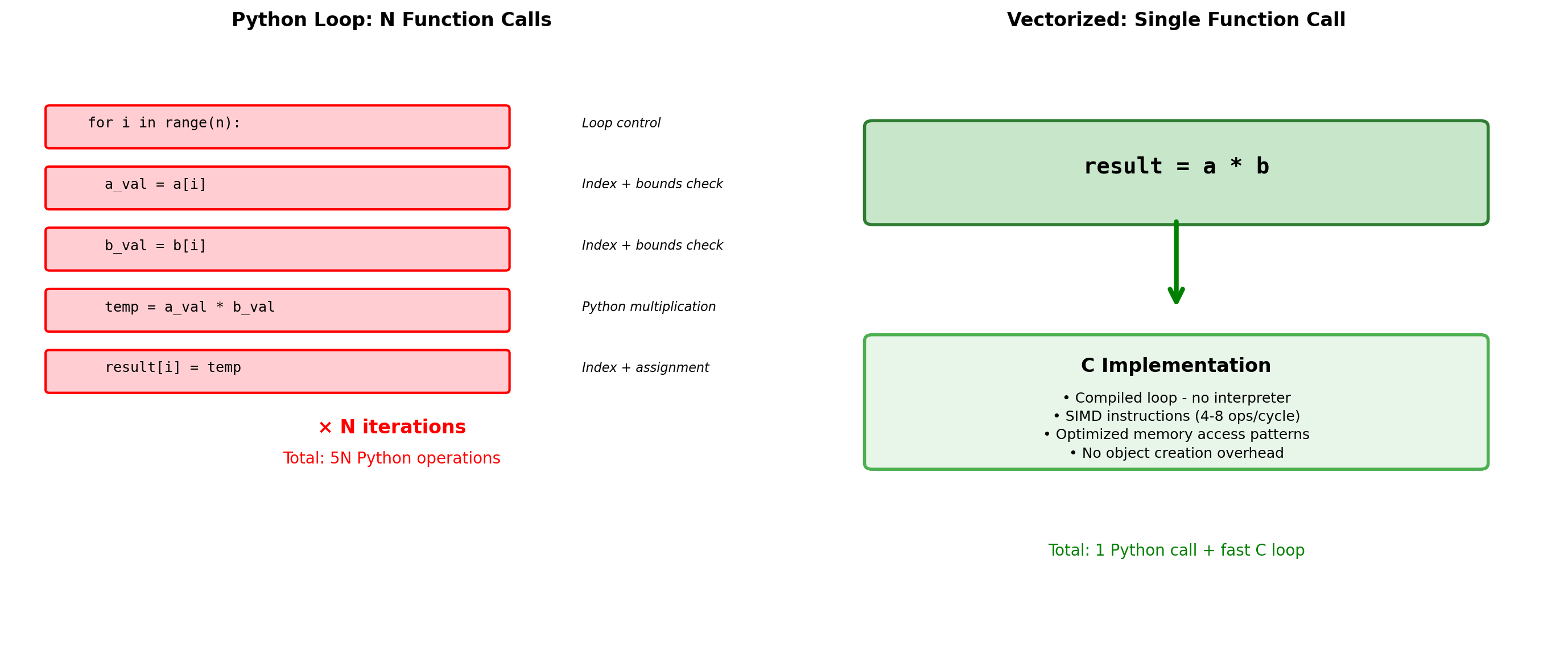
import numpy as np
import timeit
# Demonstrate vectorization impact
def element_wise_python(a, b):
"""Element-wise operations in Python."""
result = []
for i in range(len(a)):
result.append(a[i] * b[i] + 1.0)
return result
def element_wise_vectorized(a, b):
"""Vectorized operations."""
return a * b + 1.0
def mathematical_function_python(x):
"""Complex math in Python loop."""
result = []
for val in x:
result.append(val**2 + np.sin(val) + np.exp(-val))
return result
def mathematical_function_vectorized(x):
"""Complex math vectorized."""
return x**2 + np.sin(x) + np.exp(-x)
# Performance comparison
sizes = [100, 1000, 10000, 100000]
print("Vectorization performance scaling:")
print("Size | Python | NumPy | Speedup")
print("-" * 40)
for size in sizes:
# Create test data
a_list = [float(i) for i in range(size)]
b_list = [float(i+1) for i in range(size)]
a_array = np.array(a_list)
b_array = np.array(b_list)
# Reduce iterations for larger arrays
iterations = max(1, 1000 // size)
# Time Python version
t_python = timeit.timeit(
lambda: element_wise_python(a_list, b_list),
number=iterations
)
# Time NumPy version
t_numpy = timeit.timeit(
lambda: element_wise_vectorized(a_array, b_array),
number=iterations
)
speedup = t_python / t_numpy if t_numpy > 0 else float('inf')
print(f"{size:5d} | {t_python:.4f} | {t_numpy:.4f} | {speedup:5.0f}x")
# Complex mathematical operations
print(f"\nComplex mathematical functions (size 10,000):")
x_list = [i * 0.01 for i in range(10000)]
x_array = np.array(x_list)
t_math_python = timeit.timeit(
lambda: mathematical_function_python(x_list),
number=10
)
t_math_numpy = timeit.timeit(
lambda: mathematical_function_vectorized(x_array),
number=10
)
print(f" Python loop: {t_math_python:.3f}s")
print(f" Vectorized: {t_math_numpy:.3f}s")
print(f" Speedup: {t_math_python/t_math_numpy:.0f}x")
# Memory allocation overhead
def analyze_memory_pattern():
"""Show memory allocation in vectorized operations."""
x = np.arange(1000000)
# Multiple operations - intermediate arrays
result1 = x * 2 # Creates intermediate array
result2 = result1 + 1 # Creates another intermediate
result3 = result2 ** 2 # Creates final result
# Combined operation - fewer intermediates
result_combined = (x * 2 + 1) ** 2
return len([result1, result2, result3, result_combined])
print(f"\nMemory efficiency:")
print(f" Intermediate arrays created in vectorized operations")
print(f" Combine operations when possible: (x * 2 + 1) ** 2")
print(f" vs separate: temp1 = x * 2; temp2 = temp1 + 1; result = temp2 ** 2")
# Function overhead demonstration
def tiny_function(x):
return x + 1
x = np.arange(100000)
# Apply function element-wise (slow)
t_apply = timeit.timeit(
lambda: np.array([tiny_function(val) for val in x]),
number=10
)
# Vectorized equivalent (fast)
t_vector = timeit.timeit(
lambda: x + 1,
number=10
)
print(f"\nFunction call overhead (100,000 elements):")
print(f" Element-wise function: {t_apply:.3f}s")
print(f" Vectorized operation: {t_vector:.3f}s")
print(f" Overhead cost: {t_apply/t_vector:.0f}x slower")Vectorization performance scaling:
Size | Python | NumPy | Speedup
----------------------------------------
100 | 0.0000 | 0.0000 | 2x
1000 | 0.0000 | 0.0000 | 7x
10000 | 0.0003 | 0.0000 | 6x
100000 | 0.0027 | 0.0014 | 2x
Complex mathematical functions (size 10,000):
Python loop: 0.071s
Vectorized: 0.001s
Speedup: 92x
Memory efficiency:
Intermediate arrays created in vectorized operations
Combine operations when possible: (x * 2 + 1) ** 2
vs separate: temp1 = x * 2; temp2 = temp1 + 1; result = temp2 ** 2
Function call overhead (100,000 elements):
Element-wise function: 0.073s
Vectorized operation: 0.000s
Overhead cost: 467x slowerVectorization principles:
- Eliminate explicit loops - Let NumPy handle iteration in C
- Use array operations -
+,*,**work element-wise - Leverage NumPy functions -
np.sin(),np.exp()are vectorized - Minimize intermediate arrays - Combine operations when possible
- Avoid Python functions in loops - Function call overhead dominates
Advanced Indexing and Fancy Indexing
NumPy provides sophisticated indexing mechanisms that go beyond basic slicing, enabling powerful data selection and manipulation.
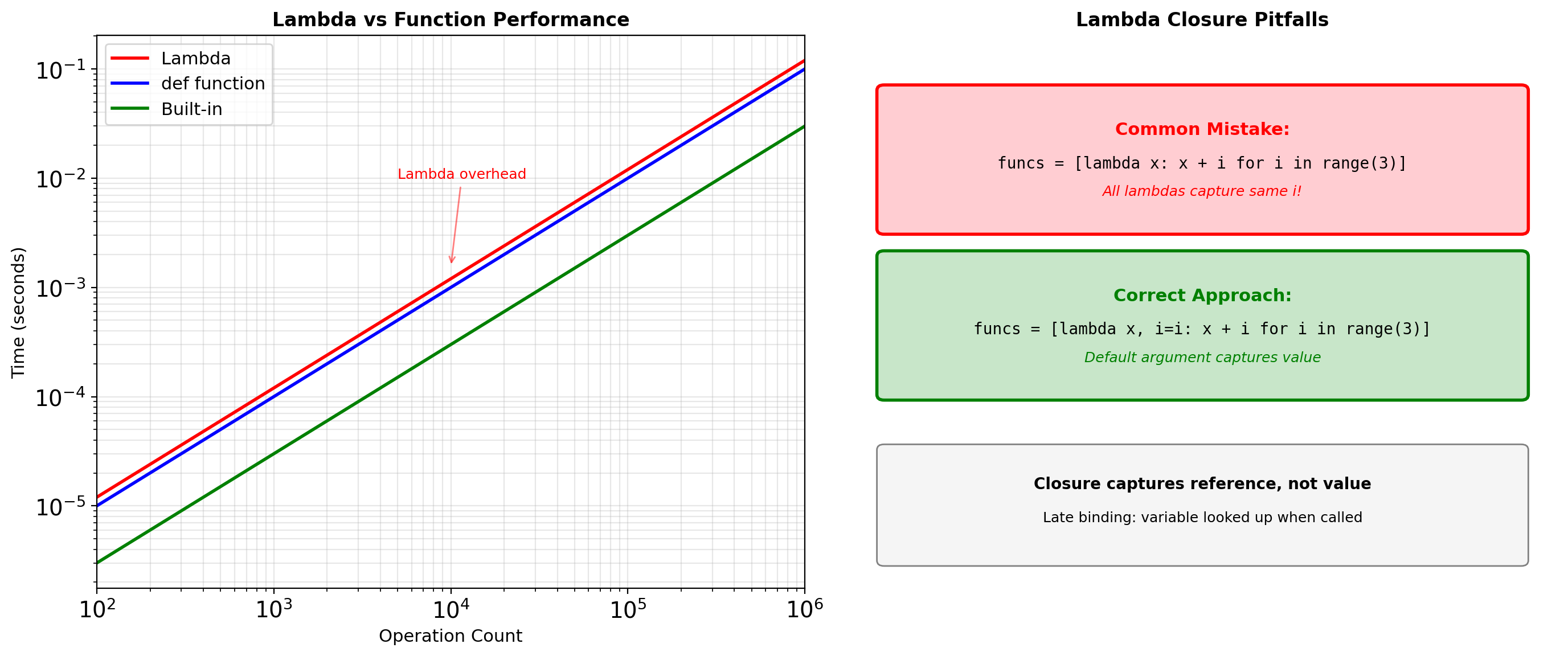
import numpy as np
import timeit
# Advanced indexing demonstration
data = np.arange(20).reshape(4, 5)
print("Original array:")
print(data)
# Boolean indexing
print("\nBoolean indexing (data > 10):")
mask = data > 10
print(f"Mask shape: {mask.shape}")
print(f"Result: {data[mask]}") # Returns 1D array
print(f"Result shape: {data[mask].shape}")
# Fancy indexing with lists
print("\nFancy indexing with row selection:")
row_indices = [0, 2, 3]
selected_rows = data[row_indices]
print(f"Selected rows {row_indices}:")
print(selected_rows)
# 2D fancy indexing
print("\nFancy indexing for specific elements:")
rows = [0, 1, 2]
cols = [1, 3, 4]
elements = data[rows, cols] # Selects (0,1), (1,3), (2,4)
print(f"Elements at (0,1), (1,3), (2,4): {elements}")
# Mixed indexing
print("\nMixed indexing (slice + fancy):")
mixed = data[:, [1, 3]] # All rows, columns 1 and 3
print(mixed)
# Where function for conditional selection
print("\nUsing np.where for conditional operations:")
result = np.where(data > 10, data, 0) # Replace values ≤10 with 0
print("Values > 10 kept, others become 0:")
print(result)
# Performance analysis
def compare_indexing_performance():
"""Compare different indexing approaches."""
size = 100000
arr = np.random.randint(0, 100, size)
# Boolean indexing
t_boolean = timeit.timeit(
lambda: arr[arr > 50],
number=100
)
# Fancy indexing
indices = np.where(arr > 50)[0]
t_fancy = timeit.timeit(
lambda: arr[indices],
number=100
)
# Basic slicing (for comparison)
t_slice = timeit.timeit(
lambda: arr[10000:20000],
number=100
)
return t_boolean, t_fancy, t_slice
t_bool, t_fancy, t_slice = compare_indexing_performance()
print(f"\nIndexing performance (100,000 elements, 100 iterations):")
print(f" Basic slicing: {t_slice:.3f}s (creates view)")
print(f" Boolean indexing: {t_bool:.3f}s ({t_bool/t_slice:.0f}x slower)")
print(f" Fancy indexing: {t_fancy:.3f}s ({t_fancy/t_slice:.0f}x slower)")
# Memory implications
large_array = np.random.rand(10000, 1000)
bool_mask = large_array > 0.5
print(f"\nMemory implications:")
print(f" Original array: {large_array.nbytes / 1024**2:.1f} MB")
print(f" Boolean mask: {bool_mask.nbytes / 1024**2:.1f} MB")
print(f" Boolean result: {large_array[bool_mask].nbytes / 1024**2:.1f} MB")
# Advanced boolean operations
print(f"\nComplex boolean operations:")
arr = np.random.randint(0, 20, (5, 5))
print("Array:")
print(arr)
# Multiple conditions
complex_mask = (arr > 5) & (arr < 15) # Element-wise AND
print(f"\nElements between 5 and 15: {arr[complex_mask]}")
# Any/all operations
print(f"Any element > 15: {np.any(arr > 15)}")
print(f"All elements > 0: {np.all(arr > 0)}")
# Axis-specific operations
print(f"Rows with any element > 15: {np.any(arr > 15, axis=1)}")
print(f"Columns with all elements > 5: {np.all(arr > 5, axis=0)}")Original array:
[[ 0 1 2 3 4]
[ 5 6 7 8 9]
[10 11 12 13 14]
[15 16 17 18 19]]
Boolean indexing (data > 10):
Mask shape: (4, 5)
Result: [11 12 13 14 15 16 17 18 19]
Result shape: (9,)
Fancy indexing with row selection:
Selected rows [0, 2, 3]:
[[ 0 1 2 3 4]
[10 11 12 13 14]
[15 16 17 18 19]]
Fancy indexing for specific elements:
Elements at (0,1), (1,3), (2,4): [ 1 8 14]
Mixed indexing (slice + fancy):
[[ 1 3]
[ 6 8]
[11 13]
[16 18]]
Using np.where for conditional operations:
Values > 10 kept, others become 0:
[[ 0 0 0 0 0]
[ 0 0 0 0 0]
[ 0 11 12 13 14]
[15 16 17 18 19]]
Indexing performance (100,000 elements, 100 iterations):
Basic slicing: 0.000s (creates view)
Boolean indexing: 0.026s (2750x slower)
Fancy indexing: 0.003s (266x slower)
Memory implications:
Original array: 76.3 MB
Boolean mask: 9.5 MB
Boolean result: 38.1 MB
Complex boolean operations:
Array:
[[ 2 5 13 12 19]
[18 10 19 7 10]
[ 3 11 13 11 19]
[ 7 7 17 3 13]
[17 10 5 9 5]]
Elements between 5 and 15: [13 12 10 7 10 11 13 11 7 7 13 10 9]
Any element > 15: True
All elements > 0: True
Rows with any element > 15: [ True True True True True]
Columns with all elements > 5: [False False False False False]Indexing creates views vs copies:
- Basic slicing: Creates views (shares memory)
- Boolean indexing: Always creates copies
- Fancy indexing: Always creates copies
- Views are faster but copies are safer
Array Creation Methods
NumPy provides multiple ways to create arrays, each optimized for different use cases.
| Method | Use case | Example |
|---|---|---|
np.array() |
From existing data | np.array([1, 2, 3]) |
np.zeros() |
Initialize to zero | np.zeros((3, 4)) |
np.ones() |
Initialize to one | np.ones((2, 3)) |
np.full() |
Initialize to value | np.full((2, 2), 7) |
np.empty() |
Uninitialized (fast) | np.empty((100, 100)) |
np.eye() |
Identity matrix | np.eye(4) |
np.diag() |
Diagonal matrix | np.diag([1, 2, 3]) |
| Method | Use case | Example |
|---|---|---|
np.arange() |
Integer sequence | np.arange(0, 10, 2) |
np.linspace() |
N evenly spaced | np.linspace(0, 1, 50) |
np.logspace() |
Log-spaced | np.logspace(0, 3, 4) |
np.meshgrid() |
Coordinate grids | np.meshgrid(x, y) |
rng.random() |
Uniform random | rng.random((3, 3)) |
rng.normal() |
Gaussian random | rng.normal(0, 1, (100,)) |
rng.integers() |
Random integers | rng.integers(0, 10, 5) |
import numpy as np
rng = np.random.default_rng(42)
# Common patterns
zeros = np.zeros((2, 3))
sequence = np.linspace(0, 1, 5)
grid_x, grid_y = np.meshgrid(np.arange(3), np.arange(2))
random_data = rng.normal(0, 1, (2, 3))
print(f"zeros:\n{zeros}")
print(f"linspace: {sequence}")
print(f"random:\n{random_data}")zeros:
[[0. 0. 0.]
[0. 0. 0.]]
linspace: [0. 0.25 0.5 0.75 1. ]
random:
[[ 0.30471708 -1.03998411 0.7504512 ]
[ 0.94056472 -1.95103519 -1.30217951]]Universal Functions (Ufuncs)
Universal functions operate element-wise on arrays. They are the building blocks of vectorized computation.
Arithmetic:
| Operation | Function | Example |
|---|---|---|
| Add | +, np.add |
a + b |
| Subtract | -, np.subtract |
a - b |
| Multiply | *, np.multiply |
a * b |
| Divide | /, np.divide |
a / b |
| Power | **, np.power |
a ** 2 |
| Modulo | %, np.mod |
a % 2 |
Comparison (returns boolean array):
| Operation | Function |
|---|---|
| Equal | ==, np.equal |
| Not equal | !=, np.not_equal |
| Less than | <, np.less |
| Greater than | >, np.greater |
Mathematical:
| Function | Description |
|---|---|
np.sin, np.cos, np.tan |
Trigonometric |
np.arcsin, np.arccos |
Inverse trig |
np.exp, np.log, np.log10 |
Exponential/log |
np.sqrt, np.square |
Root/power |
np.abs, np.sign |
Absolute/sign |
np.floor, np.ceil, np.round |
Rounding |
Key property: All ufuncs support broadcasting.
Array Manipulation
Reshaping:
import numpy as np
arr = np.arange(12)
# Reshape (view when possible)
matrix = arr.reshape(3, 4)
print(f"reshape(3, 4):\n{matrix}")
# -1 infers dimension
auto = arr.reshape(2, -1)
print(f"reshape(2, -1):\n{auto}")
# Flatten (copy) vs ravel (view)
flat = matrix.flatten() # always copy
rav = matrix.ravel() # view if possiblereshape(3, 4):
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]
reshape(2, -1):
[[ 0 1 2 3 4 5]
[ 6 7 8 9 10 11]]Combining arrays:
a = np.array([[1, 2], [3, 4]])
b = np.array([[5, 6], [7, 8]])
# Stack vertically
v = np.vstack([a, b])
print(f"vstack:\n{v}")
# Stack horizontally
h = np.hstack([a, b])
print(f"hstack:\n{h}")
# Concatenate along axis
c = np.concatenate([a, b], axis=0)vstack:
[[1 2]
[3 4]
[5 6]
[7 8]]
hstack:
[[1 2 5 6]
[3 4 7 8]]Transpose: arr.T or np.transpose(arr) - swaps axes (creates view)
Reductions and Aggregations
Reduction operations collapse an array along one or more axes.
import numpy as np
arr = np.array([[1, 2, 3],
[4, 5, 6]])
print(f"Array:\n{arr}")
print(f"sum(): {arr.sum()}") # All elements
print(f"sum(axis=0): {arr.sum(axis=0)}") # Column sums
print(f"sum(axis=1): {arr.sum(axis=1)}") # Row sumsArray:
[[1 2 3]
[4 5 6]]
sum(): 21
sum(axis=0): [5 7 9]
sum(axis=1): [ 6 15]Common reductions:
| Function | Description |
|---|---|
sum, prod |
Sum, product |
mean, std, var |
Statistics |
min, max |
Extrema |
argmin, argmax |
Index of extrema |
any, all |
Boolean reductions |
cumsum, cumprod |
Cumulative |
Axis convention: axis=0 operates along rows (collapses rows), axis=1 operates along columns.
# Practical example: normalize each row to sum to 1
data = np.array([[1, 2, 3], [4, 5, 6]], dtype=float)
row_sums = data.sum(axis=1, keepdims=True) # keepdims preserves shape for broadcasting
normalized = data / row_sums
print(f"Normalized rows:\n{normalized}")
print(f"Row sums verify: {normalized.sum(axis=1)}")Normalized rows:
[[0.16666667 0.33333333 0.5 ]
[0.26666667 0.33333333 0.4 ]]
Row sums verify: [1. 1.]Linear Algebra Essentials
NumPy provides fundamental linear algebra operations. For advanced needs, use scipy.linalg.
Matrix multiplication:
import numpy as np
A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])
x = np.array([1, 2])
# Matrix-matrix: @ operator (Python 3.5+)
print(f"A @ B:\n{A @ B}")
# Matrix-vector
print(f"A @ x: {A @ x}")
# Element-wise (NOT matrix multiply)
print(f"A * B:\n{A * B}")A @ B:
[[19 22]
[43 50]]
A @ x: [ 5 11]
A * B:
[[ 5 12]
[21 32]]Common operations:
| Function | Description |
|---|---|
A @ B |
Matrix multiply |
np.dot(A, B) |
Dot product |
np.linalg.inv(A) |
Inverse |
np.linalg.det(A) |
Determinant |
np.linalg.eig(A) |
Eigenvalues/vectors |
np.linalg.svd(A) |
SVD decomposition |
np.linalg.solve(A, b) |
Solve Ax = b |
np.linalg.norm(x) |
Vector/matrix norm |
Data Types and Memory
NumPy arrays have fixed data types. Choosing the right dtype affects memory, precision, and performance.
Common dtypes:
| Type | Description | Bytes |
|---|---|---|
float64 |
Default float | 8 |
float32 |
Single precision | 4 |
int64 |
Default integer | 8 |
int32 |
32-bit integer | 4 |
bool |
Boolean | 1 |
complex128 |
Complex | 16 |
Memory calculation:
nbytes = itemsize × size
import numpy as np
# Memory impact of dtype choice
n = 1_000_000
f64 = np.zeros(n, dtype=np.float64)
f32 = np.zeros(n, dtype=np.float32)
print(f"float64: {f64.nbytes / 1e6:.1f} MB")
print(f"float32: {f32.nbytes / 1e6:.1f} MB")
# Type conversion
arr = np.array([1.7, 2.3, 3.9])
print(f"float: {arr}")
print(f"as int: {arr.astype(np.int32)}")float64: 8.0 MB
float32: 4.0 MB
float: [1.7 2.3 3.9]
as int: [1 2 3]Precision warning: float32 has ~7 significant digits. For numerical algorithms (gradient descent, matrix decompositions), use float64 unless memory-constrained.
Random Numbers and Stochastic Methods
Pseudorandom Number Generation
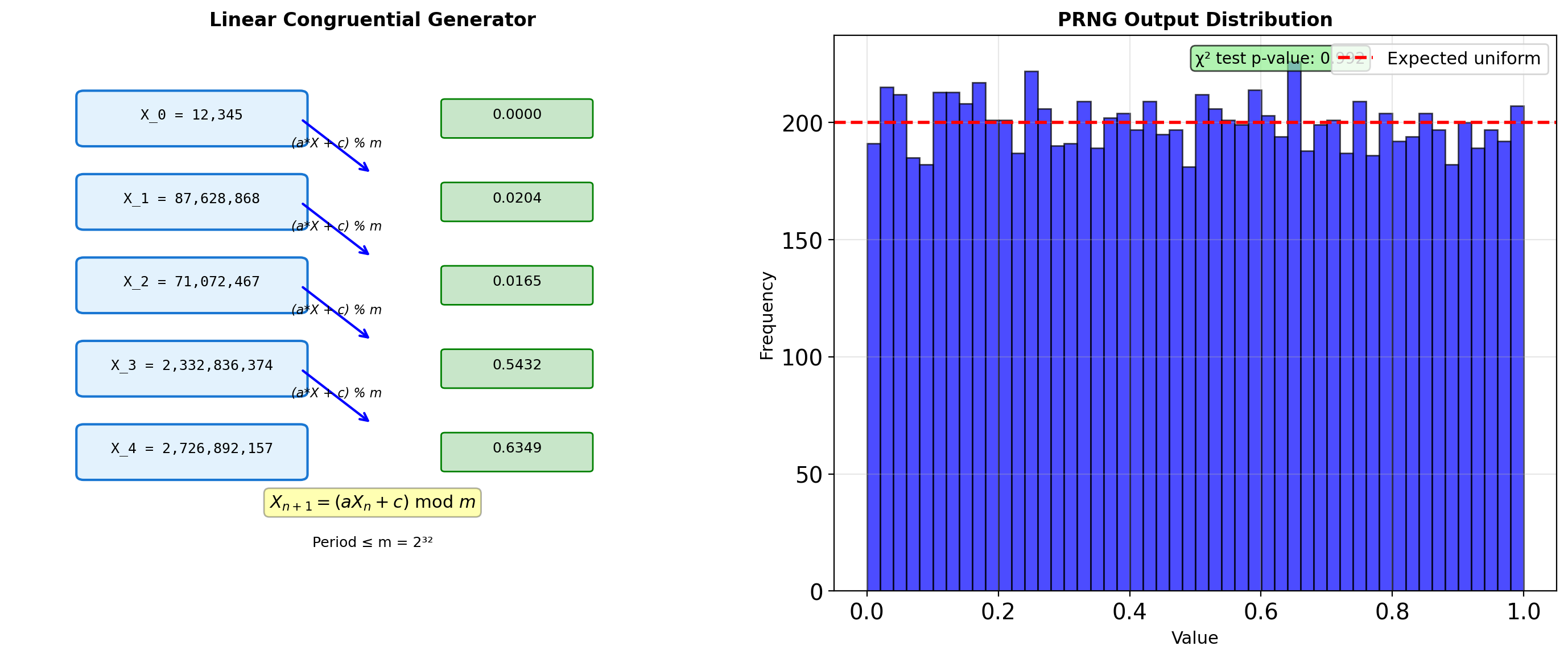
LCG (Linear Congruential Generator):
\[X_{n+1} = (aX_n + c) \mod m\]
- Simple, fast, but limited period (≤ m)
- Used historically; now superseded
Modern generator properties:
- Period: MT19937 has period 2^19937-1
- Quality: Pass TestU01 BigCrush (160 statistical tests)
- Speed: PCG64 is faster than MT19937
- State size: PCG64 uses 128 bits vs MT’s 19937 bits
PRNG output is deterministic given the seed — this enables reproducibility.
# Modern generators comparison
import numpy as np
import time
# Different PRNG algorithms
generators = {
'PCG64': np.random.PCG64,
'MT19937': np.random.MT19937, # Mersenne Twister
'Philox': np.random.Philox,
'SFC64': np.random.SFC64,
}
print("Generator properties:")
for name, gen_class in generators.items():
gen = np.random.Generator(gen_class(seed=42))
# Generate samples for timing
start = time.perf_counter()
samples = gen.random(1000000)
elapsed = time.perf_counter() - start
print(f"\n{name}:")
print(f" Time for 1M: {elapsed:.3f}s")
print(f" Mean: {samples.mean():.6f}")
print(f" Std: {samples.std():.6f}")
# State size comparison
mt = np.random.MT19937(seed=42)
pcg = np.random.PCG64(seed=42)
print(f"\nState size:")
print(f" MT19937: {len(mt.state['state']['key'])} × 32 bits")
print(f" PCG64: 2 × 64 bits")Generator properties:
PCG64:
Time for 1M: 0.004s
Mean: 0.500026
Std: 0.288635
MT19937:
Time for 1M: 0.003s
Mean: 0.499778
Std: 0.288707
Philox:
Time for 1M: 0.004s
Mean: 0.499806
Std: 0.288525
SFC64:
Time for 1M: 0.003s
Mean: 0.499989
Std: 0.288734
State size:
MT19937: 624 × 32 bits
PCG64: 2 × 64 bitsNumPy Random Architecture
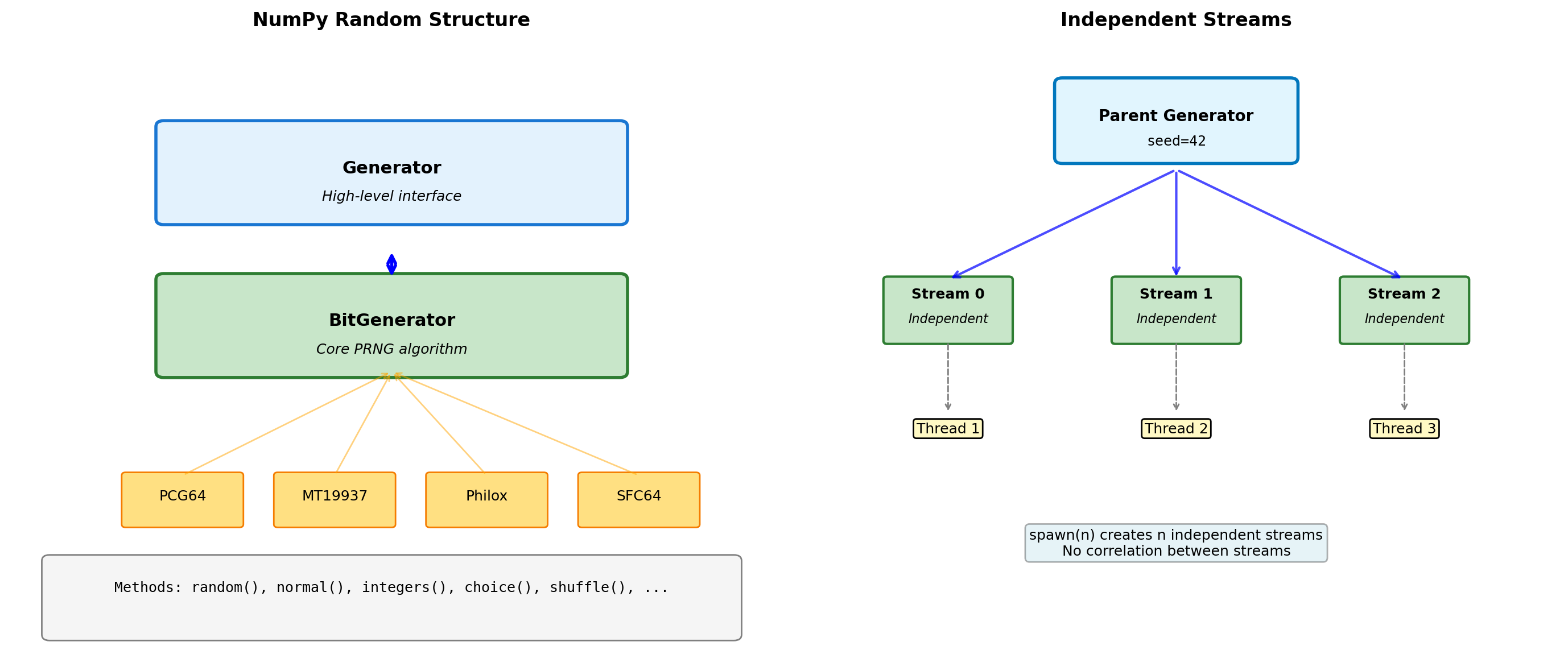
import numpy as np
# Modern NumPy random (v1.17+)
rng = np.random.default_rng(seed=42)
# Basic generation
print("Uniform [0, 1):", rng.random(5))
print("Integers [0, 10):", rng.integers(0, 10, size=5))
print("Normal(0, 1):", rng.normal(0, 1, size=5))
# Generator state management
initial_state = rng.bit_generator.state
# Generate some numbers
vals1 = rng.random(3)
print(f"\nFirst draw: {vals1}")
# Restore state
rng.bit_generator.state = initial_state
vals2 = rng.random(3)
print(f"After restore: {vals2}")
print(f"Same values: {np.array_equal(vals1, vals2)}")
# Spawn independent streams
parent_rng = np.random.default_rng(seed=42)
child_rngs = parent_rng.spawn(3)
print("\nIndependent streams:")
for i, child in enumerate(child_rngs):
print(f" Stream {i}: {child.random(3)}")Uniform [0, 1): [0.77395605 0.43887844 0.85859792 0.69736803 0.09417735]
Integers [0, 10): [5 9 7 7 7]
Normal(0, 1): [-0.01680116 -0.85304393 0.87939797 0.77779194 0.0660307 ]
First draw: [0.82276161 0.4434142 0.22723872]
After restore: [0.82276161 0.4434142 0.22723872]
Same values: True
Independent streams:
Stream 0: [0.91674416 0.91098667 0.8765925 ]
Stream 1: [0.46749078 0.0464489 0.59551001]
Stream 2: [0.0712392 0.71015972 0.07180046]# Performance: vectorized vs loop
import time
rng = np.random.default_rng(seed=42)
n = 1000000
# Vectorized generation
start = time.perf_counter()
vec_samples = rng.normal(0, 1, size=n)
vec_time = time.perf_counter() - start
# Loop generation
start = time.perf_counter()
loop_samples = [rng.normal(0, 1) for _ in range(n)]
loop_time = time.perf_counter() - start
print(f"Generation of {n:,} normals:")
print(f" Vectorized: {vec_time:.3f}s")
print(f" Loop: {loop_time:.3f}s")
print(f" Speedup: {loop_time/vec_time:.1f}x")
# Memory layout matters
print(f"\nMemory layout:")
print(f" Vectorized: {vec_samples.flags['C_CONTIGUOUS']}")
print(f" Array strides: {vec_samples.strides}")
# Custom distribution via inverse transform
def exponential_inverse_transform(rng, rate, size):
"""Generate exponential via inverse CDF."""
u = rng.random(size)
return -np.log(1 - u) / rate
custom_exp = exponential_inverse_transform(rng, rate=2.0, size=1000)
numpy_exp = rng.exponential(scale=0.5, size=1000)
print(f"\nCustom vs NumPy exponential:")
print(f" Custom mean: {custom_exp.mean():.3f}")
print(f" NumPy mean: {numpy_exp.mean():.3f}")
print(f" Theoretical: {0.5:.3f}")Generation of 1,000,000 normals:
Vectorized: 0.005s
Loop: 0.329s
Speedup: 71.0x
Memory layout:
Vectorized: True
Array strides: (8,)
Custom vs NumPy exponential:
Custom mean: 0.507
NumPy mean: 0.497
Theoretical: 0.500Distribution Sampling
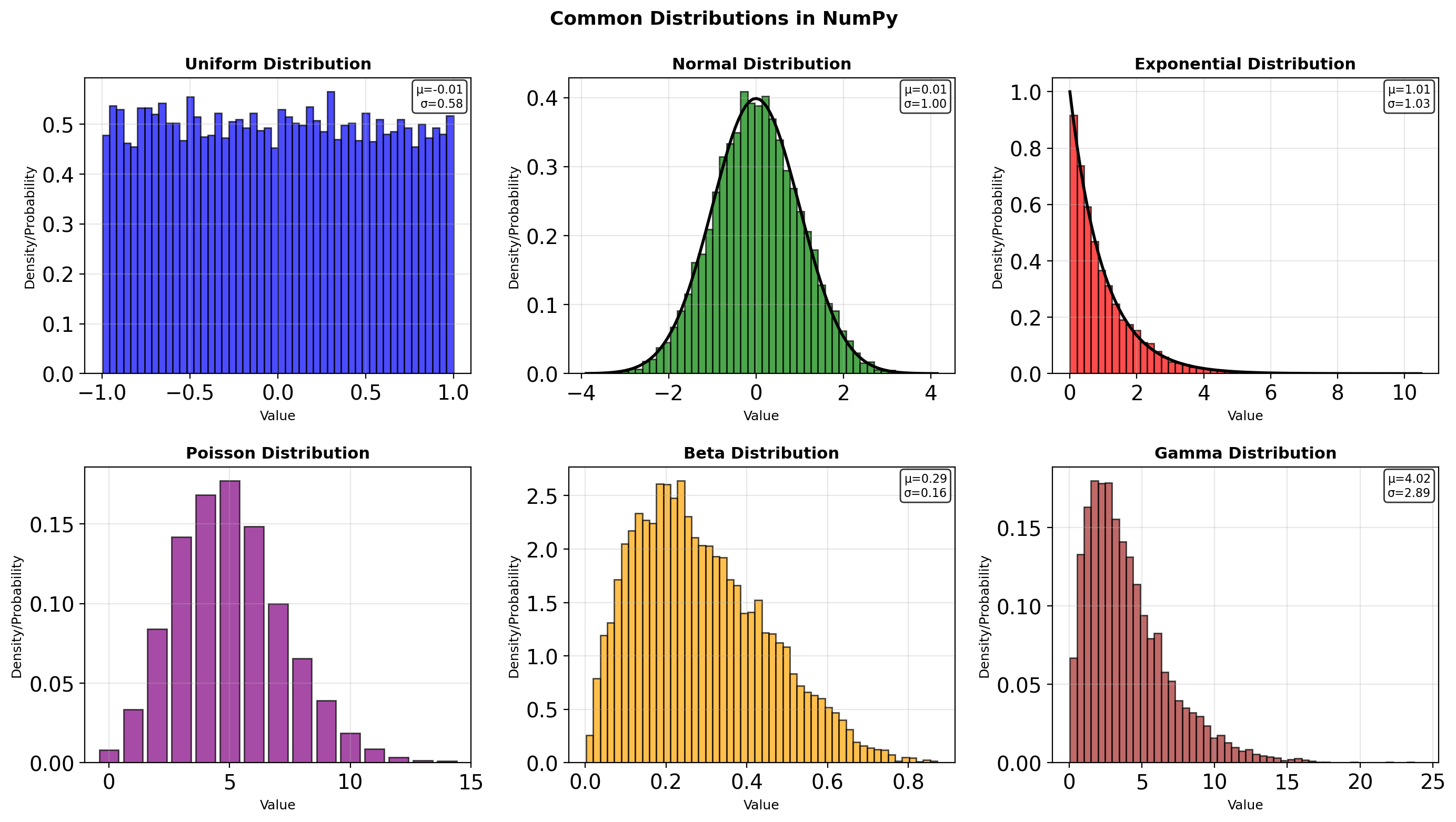
import numpy as np
from scipy import stats
rng = np.random.default_rng(seed=42)
# Sampling from various distributions
n = 1000
# Continuous distributions
uniform = rng.uniform(low=0, high=10, size=n)
normal = rng.normal(loc=100, scale=15, size=n)
exponential = rng.exponential(scale=2.0, size=n)
gamma = rng.gamma(shape=2, scale=2, size=n)
# Discrete distributions
poisson = rng.poisson(lam=3, size=n)
binomial = rng.binomial(n=10, p=0.3, size=n)
print("Sample statistics:")
print(f"Uniform[0,10]: μ={uniform.mean():.2f}, σ={uniform.std():.2f}")
print(f"Normal(100,15): μ={normal.mean():.2f}, σ={normal.std():.2f}")
print(f"Exponential(2): μ={exponential.mean():.2f}, σ={exponential.std():.2f}")
print(f"Poisson(3): μ={poisson.mean():.2f}, σ={poisson.std():.2f}")
# Multivariate distributions
mean = [0, 0]
cov = [[1, 0.5], [0.5, 1]]
multivariate = rng.multivariate_normal(mean, cov, size=1000)
print(f"\nMultivariate normal:")
print(f" Shape: {multivariate.shape}")
print(f" Correlation: {np.corrcoef(multivariate.T)[0,1]:.3f}")Sample statistics:
Uniform[0,10]: μ=4.97, σ=2.91
Normal(100,15): μ=98.83, σ=15.21
Exponential(2): μ=1.97, σ=1.96
Poisson(3): μ=2.97, σ=1.75
Multivariate normal:
Shape: (1000, 2)
Correlation: 0.459# Transformation methods
rng = np.random.default_rng(seed=42)
# Box-Muller transform for normal
def box_muller(rng, size):
"""Generate normal(0,1) from uniform."""
u1 = rng.random(size)
u2 = rng.random(size)
z0 = np.sqrt(-2 * np.log(u1)) * np.cos(2 * np.pi * u2)
z1 = np.sqrt(-2 * np.log(u1)) * np.sin(2 * np.pi * u2)
return z0, z1
z0, z1 = box_muller(rng, 5000)
print(f"Box-Muller normal:")
print(f" Mean: {z0.mean():.3f}, {z1.mean():.3f}")
print(f" Std: {z0.std():.3f}, {z1.std():.3f}")
# Rejection sampling for arbitrary distribution
def rejection_sample(pdf, bounds, rng, n_samples):
"""Sample from arbitrary PDF via rejection."""
samples = []
low, high = bounds
# Find maximum of PDF for efficiency
x_test = np.linspace(low, high, 1000)
max_pdf = np.max([pdf(x) for x in x_test])
while len(samples) < n_samples:
x = rng.uniform(low, high)
y = rng.uniform(0, max_pdf)
if y <= pdf(x):
samples.append(x)
return np.array(samples)
# Sample from beta-like distribution
pdf = lambda x: 2 * x if 0 <= x <= 1 else 0
samples = rejection_sample(pdf, (0, 1), rng, 1000)
print(f"\nRejection sampling:")
print(f" Mean: {samples.mean():.3f} (theory: 0.667)")Box-Muller normal:
Mean: -0.005, 0.000
Std: 1.002, 1.005
Rejection sampling:
Mean: 0.666 (theory: 0.667)Monte Carlo Integration
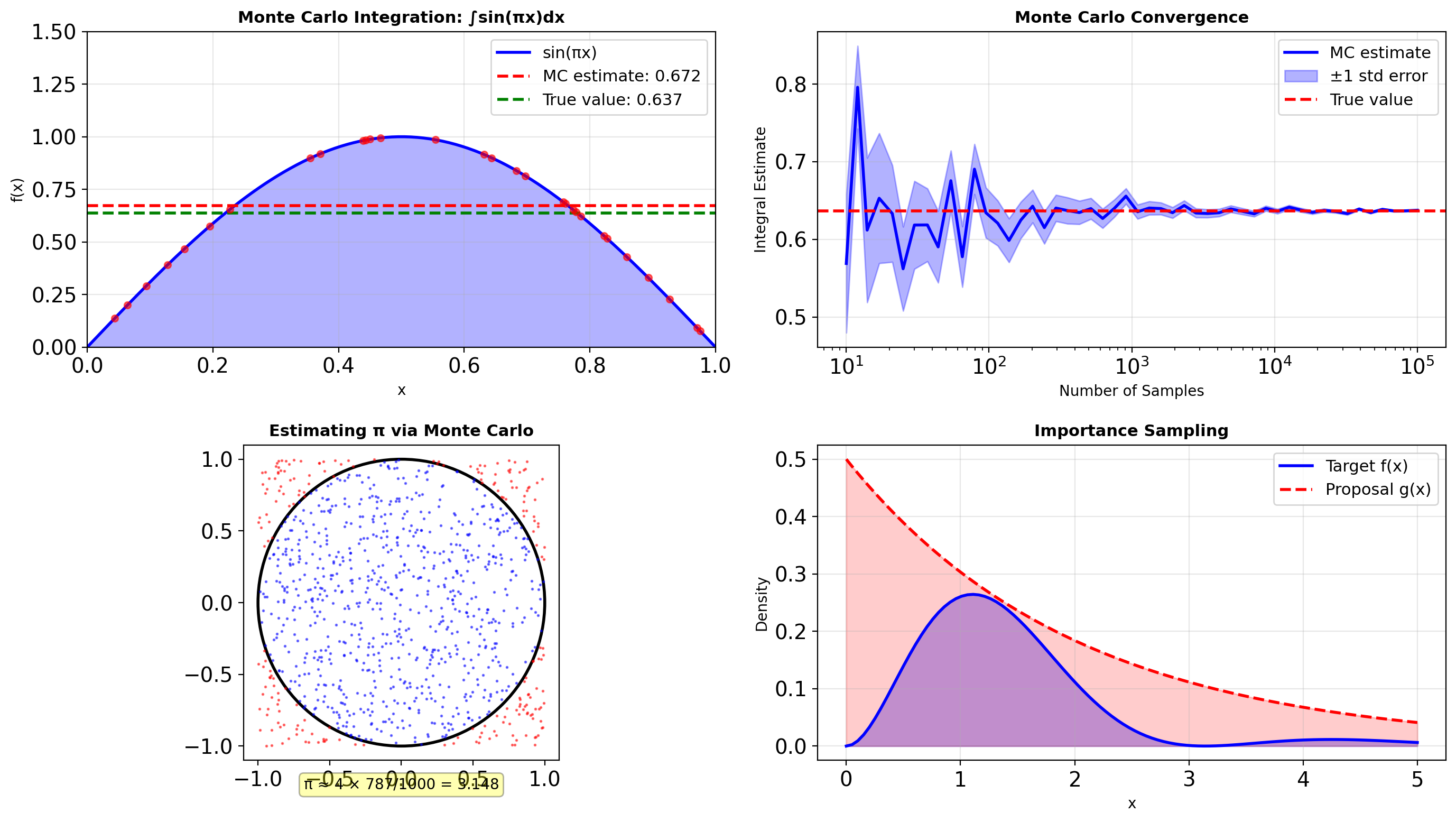
import numpy as np
def monte_carlo_integrate(func, bounds, n_samples, rng=None):
"""Basic Monte Carlo integration."""
if rng is None:
rng = np.random.default_rng()
a, b = bounds
# Sample uniformly in domain
x = rng.uniform(a, b, n_samples)
# Evaluate function
y = func(x)
# MC estimate: (b-a) * mean(f)
integral = (b - a) * np.mean(y)
std_error = (b - a) * np.std(y) / np.sqrt(n_samples)
return integral, std_error
# Example: ∫₀¹ sin(πx) dx = 2/π
rng = np.random.default_rng(seed=42)
for n in [100, 1000, 10000, 100000]:
integral, error = monte_carlo_integrate(
lambda x: np.sin(np.pi * x),
bounds=(0, 1),
n_samples=n,
rng=rng
)
true_value = 2/np.pi
print(f"n={n:6d}: {integral:.5f} ± {error:.5f} (true: {true_value:.5f})")
# Multidimensional integration
def monte_carlo_nd(func, bounds, n_samples, rng=None):
"""N-dimensional Monte Carlo integration."""
if rng is None:
rng = np.random.default_rng()
ndim = len(bounds)
volume = np.prod([b - a for a, b in bounds])
# Sample in hypercube
samples = np.zeros((n_samples, ndim))
for i, (a, b) in enumerate(bounds):
samples[:, i] = rng.uniform(a, b, n_samples)
# Evaluate function
values = np.array([func(*s) for s in samples])
integral = volume * np.mean(values)
std_error = volume * np.std(values) / np.sqrt(n_samples)
return integral, std_error
# 2D example: ∫∫ exp(-(x²+y²)) dx dy over unit square
def gaussian_2d(x, y):
return np.exp(-(x**2 + y**2))
integral_2d, error_2d = monte_carlo_nd(
gaussian_2d,
bounds=[(0, 1), (0, 1)],
n_samples=10000,
rng=rng
)
print(f"\n2D integral: {integral_2d:.5f} ± {error_2d:.5f}")n= 100: 0.67226 ± 0.02825 (true: 0.63662)
n= 1000: 0.63032 ± 0.00972 (true: 0.63662)
n= 10000: 0.63801 ± 0.00308 (true: 0.63662)
n=100000: 0.63706 ± 0.00097 (true: 0.63662)
2D integral: 0.55976 ± 0.00217# Variance reduction: stratified sampling
def stratified_monte_carlo(func, bounds, n_strata, samples_per_stratum, rng=None):
"""Stratified Monte Carlo for variance reduction."""
if rng is None:
rng = np.random.default_rng()
a, b = bounds
stratum_width = (b - a) / n_strata
estimates = []
for i in range(n_strata):
# Sample within stratum
stratum_a = a + i * stratum_width
stratum_b = a + (i + 1) * stratum_width
x = rng.uniform(stratum_a, stratum_b, samples_per_stratum)
y = func(x)
# Stratum estimate
estimates.append(np.mean(y))
# Combine strata
integral = (b - a) * np.mean(estimates)
std_error = (b - a) * np.std(estimates) / np.sqrt(n_strata)
return integral, std_error
# Compare standard vs stratified
n_total = 10000
# Standard MC
standard_int, standard_err = monte_carlo_integrate(
lambda x: np.sin(np.pi * x),
bounds=(0, 1),
n_samples=n_total,
rng=rng
)
# Stratified MC
n_strata = 100
stratified_int, stratified_err = stratified_monte_carlo(
lambda x: np.sin(np.pi * x),
bounds=(0, 1),
n_strata=n_strata,
samples_per_stratum=n_total // n_strata,
rng=rng
)
print(f"Variance reduction comparison ({n_total} samples):")
print(f" Standard: {standard_int:.5f} ± {standard_err:.5f}")
print(f" Stratified: {stratified_int:.5f} ± {stratified_err:.5f}")
print(f" Error reduction: {standard_err/stratified_err:.2f}x")Variance reduction comparison (10000 samples):
Standard: 0.63776 ± 0.00306
Stratified: 0.63655 ± 0.03078
Error reduction: 0.10xRandom Walks and Stochastic Processes
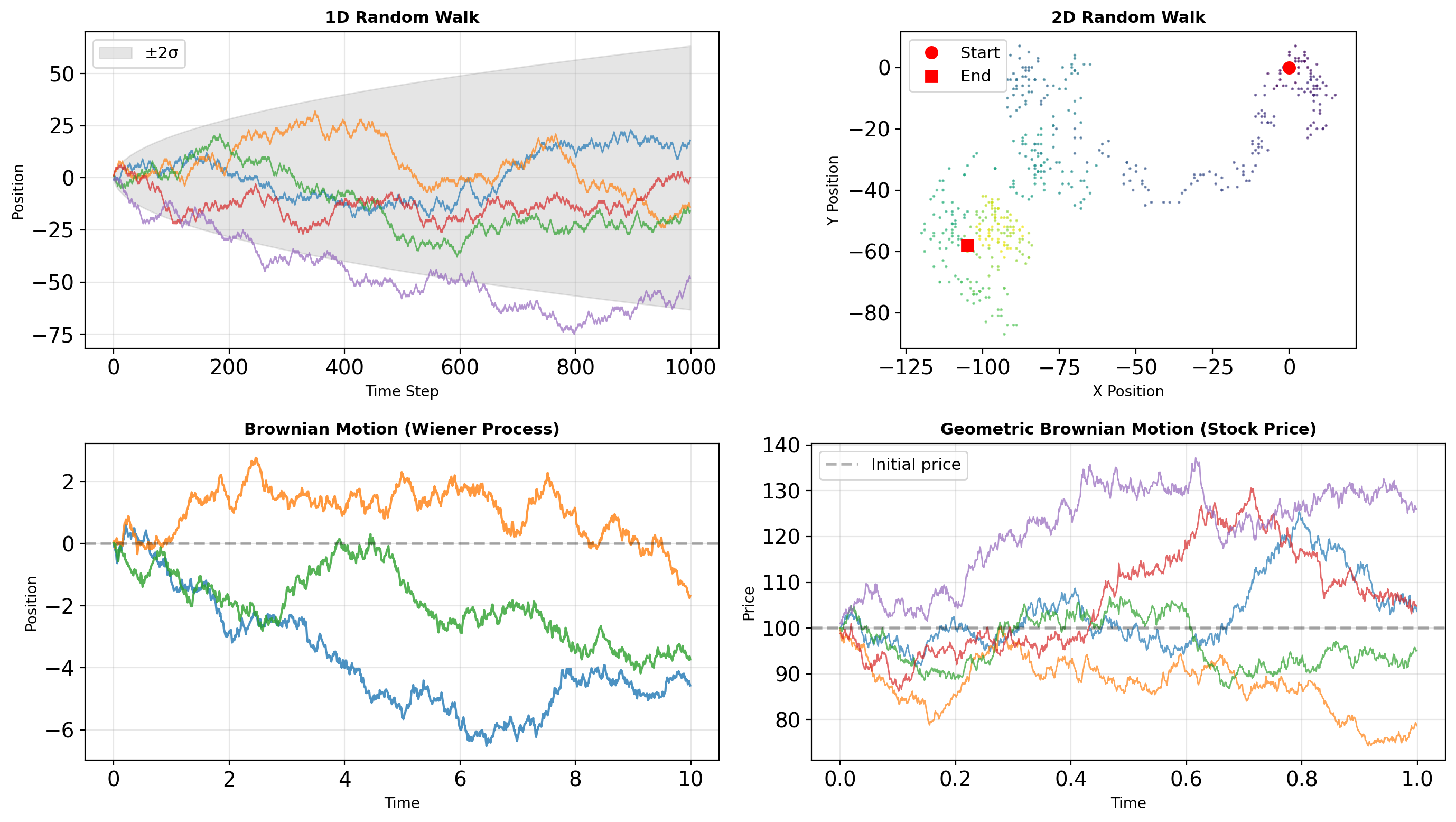
import numpy as np
class RandomWalk:
"""1D and 2D random walk simulator."""
def __init__(self, seed=None):
self.rng = np.random.default_rng(seed)
def walk_1d(self, n_steps, p_up=0.5):
"""1D random walk with bias."""
steps = self.rng.choice(
[-1, 1],
size=n_steps,
p=[1-p_up, p_up]
)
return np.cumsum(steps)
def walk_2d(self, n_steps):
"""2D random walk on lattice."""
# Possible moves: up, down, left, right
moves = np.array([[0, 1], [0, -1], [-1, 0], [1, 0]])
choices = self.rng.integers(0, 4, size=n_steps)
steps = moves[choices]
path = np.cumsum(steps, axis=0)
return path[:, 0], path[:, 1]
def first_passage_time(self, barrier, max_steps=10000):
"""Time to first reach barrier."""
position = 0
for step in range(max_steps):
position += self.rng.choice([-1, 1])
if abs(position) >= barrier:
return step + 1
return None
# Analyze random walk properties
walker = RandomWalk(seed=42)
# First passage times
barriers = [10, 20, 50]
n_trials = 1000
for barrier in barriers:
times = []
for _ in range(n_trials):
t = walker.first_passage_time(barrier)
if t is not None:
times.append(t)
mean_time = np.mean(times)
theoretical = barrier ** 2 # E[T] = n² for symmetric walk
print(f"Barrier ±{barrier}:")
print(f" Mean time: {mean_time:.1f}")
print(f" Theory: {theoretical:.1f}")
print(f" Success rate: {len(times)/n_trials:.1%}")Barrier ±10:
Mean time: 99.2
Theory: 100.0
Success rate: 100.0%
Barrier ±20:
Mean time: 405.9
Theory: 400.0
Success rate: 100.0%
Barrier ±50:
Mean time: 2384.1
Theory: 2500.0
Success rate: 99.3%# Stochastic differential equations
def euler_maruyama(sde_drift, sde_diffusion, x0, t_span, dt, rng=None):
"""Solve SDE using Euler-Maruyama method."""
if rng is None:
rng = np.random.default_rng()
t = np.arange(t_span[0], t_span[1], dt)
n = len(t)
x = np.zeros(n)
x[0] = x0
# Generate all random increments at once
dW = rng.normal(0, np.sqrt(dt), n-1)
for i in range(n-1):
drift = sde_drift(x[i], t[i])
diffusion = sde_diffusion(x[i], t[i])
x[i+1] = x[i] + drift*dt + diffusion*dW[i]
return t, x
# Ornstein-Uhlenbeck process (mean-reverting)
def ou_drift(x, t, theta=1.0, mu=0.0):
return theta * (mu - x)
def ou_diffusion(x, t, sigma=0.3):
return sigma
rng = np.random.default_rng(seed=42)
# Simulate multiple paths
print("Ornstein-Uhlenbeck process:")
for x0 in [2.0, 0.0, -2.0]:
t, x = euler_maruyama(
ou_drift, ou_diffusion,
x0=x0, t_span=(0, 10), dt=0.01,
rng=rng
)
print(f" Start: {x0:+.1f}, End: {x[-1]:+.2f}, Mean: {x[len(x)//2:].mean():+.2f}")
# Geometric Brownian Motion
def gbm_drift(S, t, mu=0.05):
return mu * S
def gbm_diffusion(S, t, sigma=0.2):
return sigma * S
t, S = euler_maruyama(
gbm_drift, gbm_diffusion,
x0=100, t_span=(0, 1), dt=0.001,
rng=rng
)
print(f"\nGBM Stock simulation:")
print(f" Initial: ${S[0]:.2f}")
print(f" Final: ${S[-1]:.2f}")
print(f" Return: {(S[-1]/S[0] - 1)*100:.1f}%")Ornstein-Uhlenbeck process:
Start: +2.0, End: +0.05, Mean: -0.15
Start: +0.0, End: -0.57, Mean: -0.38
Start: -2.0, End: +0.19, Mean: +0.13
GBM Stock simulation:
Initial: $100.00
Final: $104.77
Return: 4.8%Reproducibility and Parallel Streams
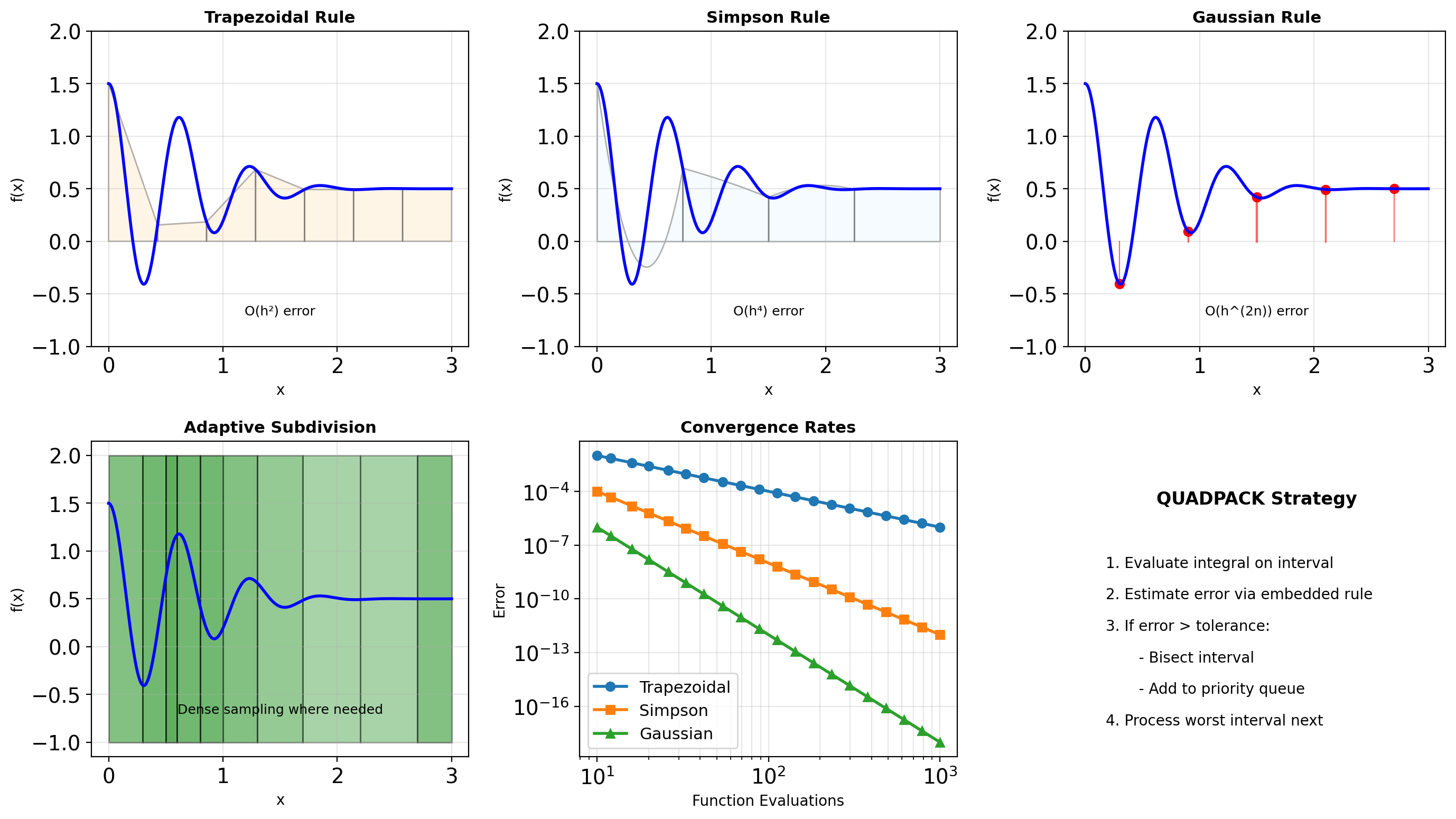
import numpy as np
from concurrent.futures import ProcessPoolExecutor
import multiprocessing as mp
def monte_carlo_pi(n_samples, seed):
"""Estimate π using Monte Carlo."""
rng = np.random.default_rng(seed)
# Generate points in unit square
x = rng.random(n_samples)
y = rng.random(n_samples)
# Count points inside circle
inside = (x**2 + y**2) <= 1
pi_estimate = 4 * inside.sum() / n_samples
return pi_estimate
# Serial execution
rng_main = np.random.default_rng(seed=42)
n_trials = 4
n_samples = 1000000
print("Serial execution:")
serial_results = []
for i in range(n_trials):
# Use different seed for each trial
seed = rng_main.integers(0, 2**32)
result = monte_carlo_pi(n_samples, seed)
serial_results.append(result)
print(f" Trial {i}: π ≈ {result:.5f}")
print(f" Mean: {np.mean(serial_results):.5f}")
print(f" Std: {np.std(serial_results):.5f}")
# Parallel execution with spawned generators
def parallel_monte_carlo():
"""Parallel MC with independent streams."""
parent_rng = np.random.default_rng(seed=42)
# Spawn independent streams
n_workers = mp.cpu_count()
child_seeds = parent_rng.spawn(n_workers)
# Create tasks with independent seeds
tasks = []
for i in range(n_workers):
# Extract seed value from SeedSequence
seed_value = child_seeds[i].generate_state(1)[0]
tasks.append((n_samples, seed_value))
return tasks
# Note: ProcessPoolExecutor not shown due to execution environment
print(f"\nParallel setup for {mp.cpu_count()} cores created")Serial execution:
Trial 0: π ≈ 3.14089
Trial 1: π ≈ 3.14045
Trial 2: π ≈ 3.14242
Trial 3: π ≈ 3.14100
Mean: 3.14119
Std: 0.00074
Parallel setup for 16 cores createdReproducibility patterns:
# Use explicit generators (not global state)
rng = np.random.default_rng(seed=42)
# Pass rng to functions explicitly
def simulate(n, rng):
return rng.normal(0, 1, n)
# Save/restore state for checkpoints
state = rng.bit_generator.state
# ... do work ...
rng.bit_generator.state = state # restore
# Use spawn() for parallel work
children = rng.spawn(4) # 4 independent streamsAvoid:
np.random.seed()— global state, not thread-safe- Creating
default_rng()without seed inside loops
Same seed + same code = identical results.
Functional Programming Patterns
Lambda Functions: Anonymous Functions in Python
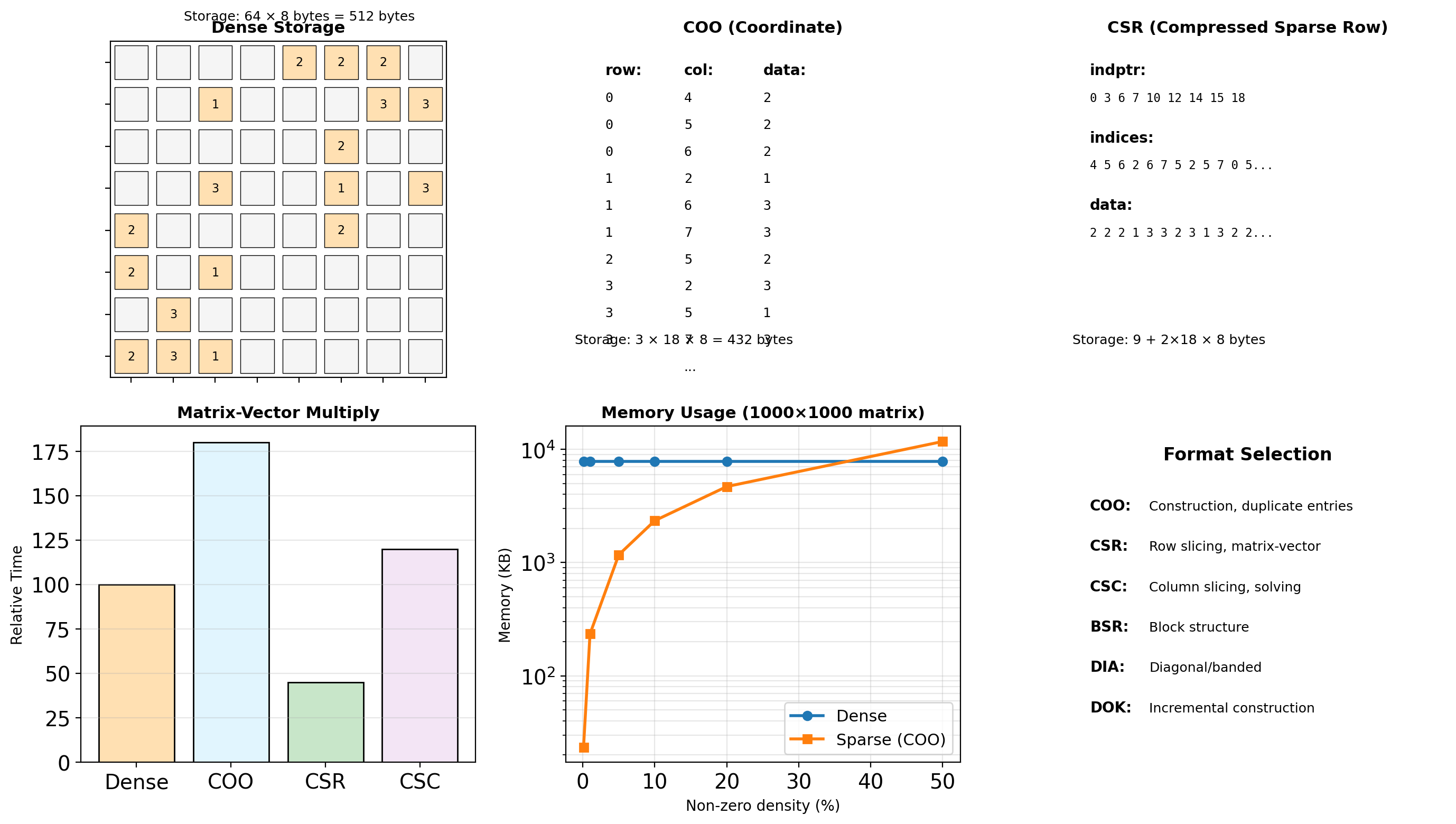
# Lambda basics
square = lambda x: x**2
add = lambda x, y: x + y
magnitude = lambda v: sum(x**2 for x in v) ** 0.5
print(f"square(5) = {square(5)}")
print(f"add(3, 4) = {add(3, 4)}")
print(f"magnitude([3, 4]) = {magnitude([3, 4])}")
# Lambda limitations - no statements
try:
# This won't work - assignment is a statement
bad_lambda = lambda x: (y := x + 1, y * 2)
except SyntaxError as e:
print(f"\nSyntax error in lambda")
# Workaround using expression forms
result = (lambda x: (x + 1) * 2)(5)
print(f"Workaround result: {result}")
# Lambda with conditional expression
abs_val = lambda x: x if x >= 0 else -x
sign = lambda x: 1 if x > 0 else (-1 if x < 0 else 0)
print(f"\nabs_val(-5) = {abs_val(-5)}")
print(f"sign(-5) = {sign(-5)}")
print(f"sign(0) = {sign(0)}")
print(f"sign(5) = {sign(5)}")square(5) = 25
add(3, 4) = 7
magnitude([3, 4]) = 5.0
Workaround result: 12
abs_val(-5) = 5
sign(-5) = -1
sign(0) = 0
sign(5) = 1# Lambdas in data processing
import numpy as np
# Sorting with custom key
points = [(3, 4), (1, 2), (5, 1), (2, 3)]
# Sort by distance from origin
by_distance = sorted(points, key=lambda p: (p[0]**2 + p[1]**2)**0.5)
print(f"By distance: {by_distance}")
# Sort by second coordinate
by_y = sorted(points, key=lambda p: p[1])
print(f"By y-coord: {by_y}")
# Complex sorting - primary and secondary keys
data = [('Alice', 85), ('Bob', 92), ('Charlie', 85), ('David', 78)]
sorted_data = sorted(data, key=lambda x: (-x[1], x[0]))
print(f"\nBy score desc, then name:")
for name, score in sorted_data:
print(f" {name}: {score}")
# Lambda in numerical operations
vectors = np.array([[1, 2], [3, 4], [5, 6]])
# Apply transformation
transform = lambda v: v / np.linalg.norm(v)
normalized = np.apply_along_axis(transform, 1, vectors)
print(f"\nNormalized vectors:")
print(normalized)By distance: [(1, 2), (2, 3), (3, 4), (5, 1)]
By y-coord: [(5, 1), (1, 2), (2, 3), (3, 4)]
By score desc, then name:
Bob: 92
Alice: 85
Charlie: 85
David: 78
Normalized vectors:
[[0.4472136 0.89442719]
[0.6 0.8 ]
[0.6401844 0.76822128]]Lambda Performance and Pitfalls

# Closure pitfall demonstration
print("Closure problem:")
funcs_bad = []
for i in range(3):
funcs_bad.append(lambda x: x + i)
# All functions use final value of i
for j, f in enumerate(funcs_bad):
print(f" func[{j}](10) = {f(10)}") # All return 12!
print("\nFixed with default argument:")
funcs_good = []
for i in range(3):
funcs_good.append(lambda x, i=i: x + i)
for j, f in enumerate(funcs_good):
print(f" func[{j}](10) = {f(10)}") # Correct: 10, 11, 12
# Alternative: use functools.partial
from functools import partial
def add(x, y):
return x + y
print("\nUsing partial:")
funcs_partial = [partial(add, y=i) for i in range(3)]
for j, f in enumerate(funcs_partial):
print(f" func[{j}](10) = {f(10)}")Closure problem:
func[0](10) = 12
func[1](10) = 12
func[2](10) = 12
Fixed with default argument:
func[0](10) = 10
func[1](10) = 11
func[2](10) = 12
Using partial:
func[0](10) = 10
func[1](10) = 11
func[2](10) = 12Closure capture rule:
Closures capture references to variables, not values. The variable is looked up when the function is called, not when it’s defined.
Fixes:
- Default argument:
lambda x, i=i: x + i functools.partial: binds value at creation time- Nested function with local binding
When lambdas are appropriate:
- Short, single-expression functions
- Throwaway functions for
sort,map,filter - Simple callbacks
Prefer named functions when:
- Logic is complex or reusable
- You need docstrings or type hints
- Debugging is important (lambdas have no name)
Map, Filter, Reduce: Functional Transformations
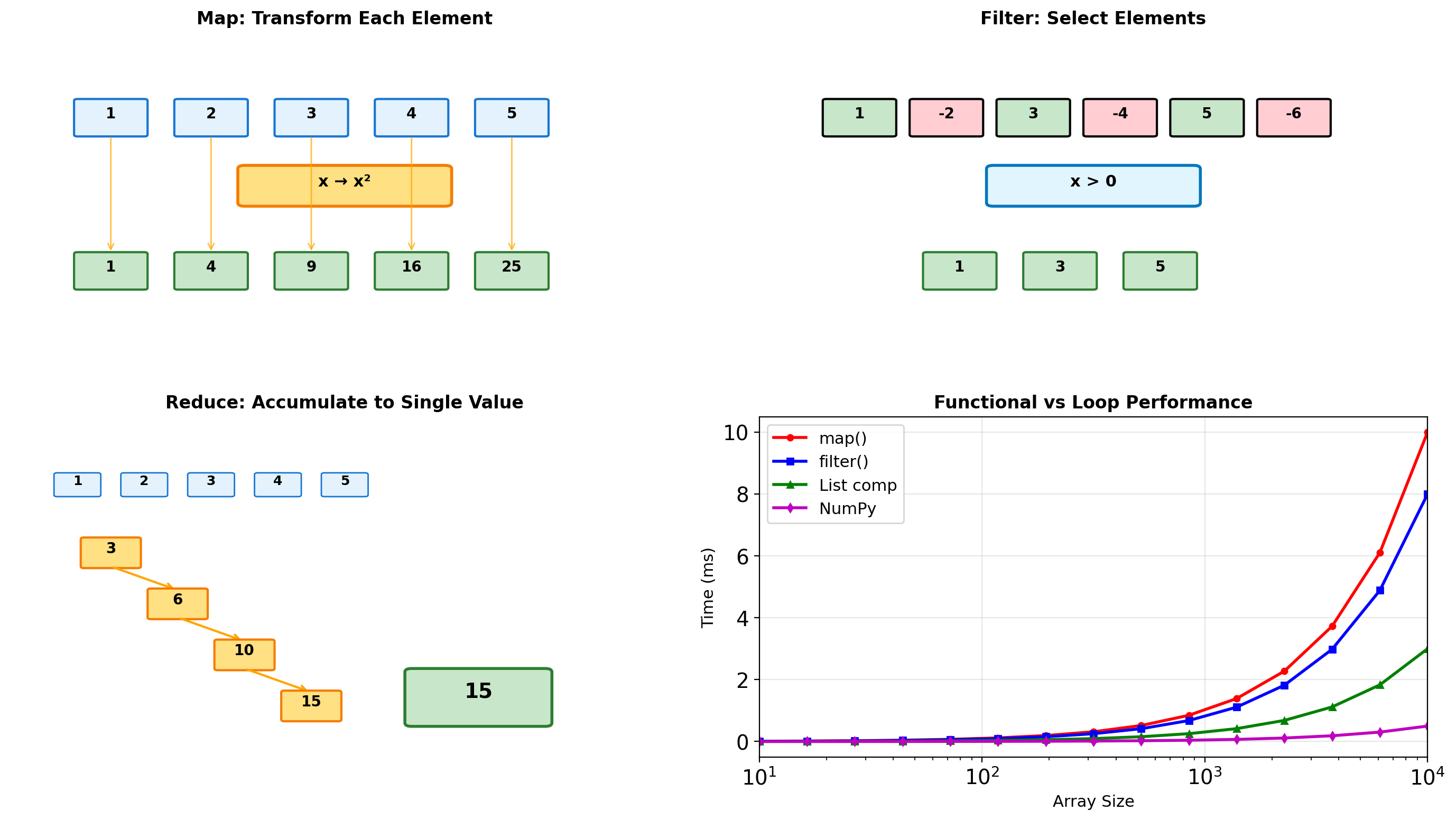
from functools import reduce
import operator
data = [1, 2, 3, 4, 5]
# Map: transform each element
squared = list(map(lambda x: x**2, data))
print(f"Original: {data}")
print(f"Squared: {squared}")
# Filter: select elements
evens = list(filter(lambda x: x % 2 == 0, data))
odds = list(filter(lambda x: x % 2 == 1, data))
print(f"\nEvens: {evens}")
print(f"Odds: {odds}")
# Reduce: accumulate to single value
sum_all = reduce(operator.add, data)
product = reduce(operator.mul, data)
max_val = reduce(lambda a, b: a if a > b else b, data)
print(f"\nSum: {sum_all}")
print(f"Product: {product}")
print(f"Max: {max_val}")
# Combining operations
result = reduce(
operator.add,
filter(
lambda x: x > 10,
map(lambda x: x**2, data)
)
)
print(f"\nSum of squares > 10: {result}")
# Functional pipeline
def pipeline(data, *functions):
"""Apply functions in sequence."""
for func in functions:
data = func(data)
return data
result = pipeline(
range(10),
lambda x: map(lambda n: n**2, x),
lambda x: filter(lambda n: n % 2 == 0, x),
list
)
print(f"\nPipeline result: {result}")Original: [1, 2, 3, 4, 5]
Squared: [1, 4, 9, 16, 25]
Evens: [2, 4]
Odds: [1, 3, 5]
Sum: 15
Product: 120
Max: 5
Sum of squares > 10: 41
Pipeline result: [0, 4, 16, 36, 64]# Performance comparison
import timeit
import numpy as np
data = list(range(1000))
# Map alternatives
t_map = timeit.timeit(
lambda: list(map(lambda x: x**2, data)),
number=1000
)
t_comp = timeit.timeit(
lambda: [x**2 for x in data],
number=1000
)
t_numpy = timeit.timeit(
lambda: np.array(data)**2,
number=1000
)
print(f"Squaring 1000 numbers:")
print(f" map(): {t_map:.3f}s")
print(f" List comp: {t_comp:.3f}s ({t_map/t_comp:.2f}x)")
print(f" NumPy: {t_numpy:.3f}s ({t_map/t_numpy:.1f}x)")
# Memory efficiency
print(f"\nMemory behavior:")
# Map returns iterator (lazy)
mapped = map(lambda x: x**2, range(1000000))
print(f" map object: {sys.getsizeof(mapped)} bytes")
# List comprehension creates full list
comp = [x**2 for x in range(100000)] # Smaller for memory
print(f" List comp (100k): {sys.getsizeof(comp):,} bytes")
# Generator expression (lazy like map)
gen = (x**2 for x in range(1000000))
print(f" Generator expr: {sys.getsizeof(gen)} bytes")
# Practical reduce example
from itertools import accumulate
# Running statistics
values = [3, 1, 4, 1, 5, 9, 2, 6]
running_sum = list(accumulate(values))
running_max = list(accumulate(values, max))
print(f"\nValues: {values}")
print(f"Running sum: {running_sum}")
print(f"Running max: {running_max}")Squaring 1000 numbers:
map(): 0.035s
List comp: 0.020s (1.78x)
NumPy: 0.027s (1.3x)
Memory behavior:
map object: 48 bytes
List comp (100k): 800,984 bytes
Generator expr: 208 bytes
Values: [3, 1, 4, 1, 5, 9, 2, 6]
Running sum: [3, 4, 8, 9, 14, 23, 25, 31]
Running max: [3, 3, 4, 4, 5, 9, 9, 9]Map, Filter, Reduce in Numerical Computing
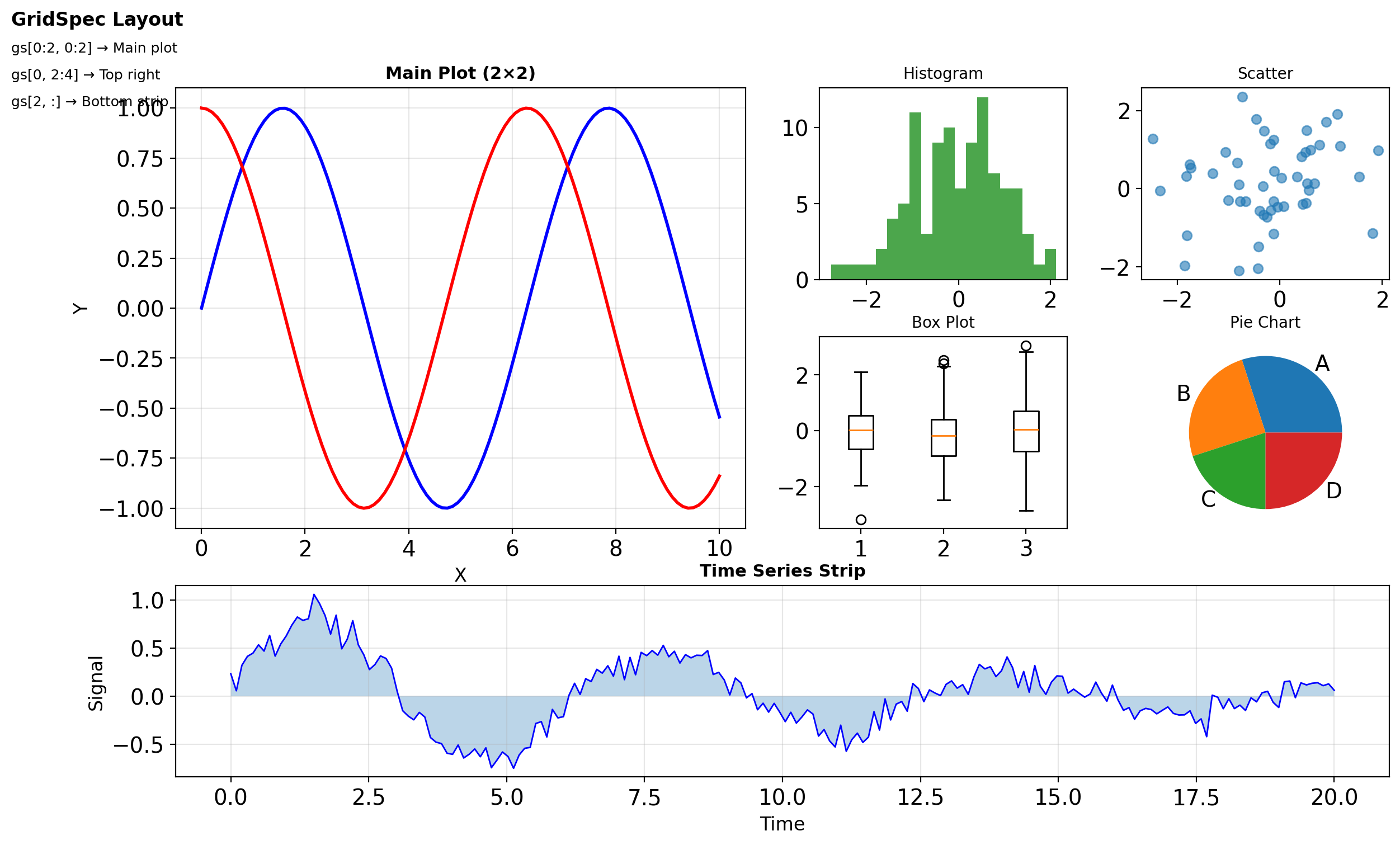
import numpy as np
from functools import reduce
# Signal processing pipeline
def process_signals(signals):
"""Functional signal processing pipeline."""
# Filter: remove invalid signals
valid = filter(lambda s: not np.any(np.isnan(s)), signals)
# Map: normalize each signal
normalized = map(lambda s: (s - s.mean()) / s.std(), valid)
# Map: compute features
features = map(lambda s: {
'energy': np.sum(s**2),
'peak': np.max(np.abs(s)),
'zero_crossings': np.sum(np.diff(np.sign(s)) != 0)
}, normalized)
return list(features)
# Generate test signals
np.random.seed(42)
signals = [
np.sin(np.linspace(0, 2*np.pi, 100)) + 0.1*np.random.randn(100),
np.random.randn(100),
np.array([np.nan] * 100), # Invalid
np.cos(np.linspace(0, 4*np.pi, 100)),
]
results = process_signals(signals)
print("Signal features:")
for i, feat in enumerate(results):
print(f" Signal {i}: energy={feat['energy']:.1f}, "
f"peak={feat['peak']:.2f}, crossings={feat['zero_crossings']}")
# Matrix operations with functional approach
def matrix_pipeline(matrix):
"""Process matrix rows functionally."""
# Filter rows by condition
filtered_rows = filter(
lambda row: np.sum(row) > 0,
matrix
)
# Normalize each row
normalized = map(
lambda row: row / np.linalg.norm(row),
filtered_rows
)
# Reduce to summary statistics
row_list = list(normalized)
if row_list:
mean_row = reduce(
lambda a, b: a + b,
row_list
) / len(row_list)
return mean_row
return None
# Test matrix
matrix = np.random.randn(10, 5)
matrix[2] = -np.abs(matrix[2]) # Make one row negative sum
result = matrix_pipeline(matrix)
print(f"\nMean normalized row: {result}")Signal features:
Signal 0: energy=100.0, peak=1.80, crossings=3
Signal 1: energy=100.0, peak=2.84, crossings=54
Signal 2: energy=100.0, peak=1.42, crossings=4
Mean normalized row: [ 0.01159341 0.05561288 -0.05330941 0.1654067 0.35741119]# Parallel map for expensive operations
from multiprocessing import Pool
import time
def expensive_computation(x):
"""Simulate expensive computation."""
# In real code, this might be optimization, simulation, etc.
result = 0
for i in range(100000):
result += x * np.sin(i) * np.cos(i)
return result / 100000
# Sequential map
data = list(range(10))
start = time.perf_counter()
sequential_results = list(map(expensive_computation, data))
seq_time = time.perf_counter() - start
print(f"Sequential map: {seq_time:.3f}s")
# Parallel map (simplified for demonstration)
# Note: In Jupyter/interactive environments, use:
# from multiprocessing.dummy import Pool # Thread pool
# Or restructure for subprocess pool
def parallel_map(func, data, n_workers=4):
"""Simple parallel map implementation."""
# Simulate parallel execution
# In production, use multiprocessing.Pool
results = []
chunk_size = len(data) // n_workers
for i in range(0, len(data), chunk_size):
chunk = data[i:i+chunk_size]
results.extend(map(func, chunk))
return results
# Lazy evaluation for large datasets
def lazy_pipeline(data_generator):
"""Process infinite/large data streams."""
# Chain of transformations (all lazy)
transformed = map(lambda x: x**2, data_generator)
filtered = filter(lambda x: x % 2 == 0, transformed)
processed = map(lambda x: x // 2, filtered)
# Only compute what's needed
return processed
# Infinite generator
def fibonacci():
a, b = 0, 1
while True:
yield a
a, b = b, a + b
# Process only first 10 values
pipeline = lazy_pipeline(fibonacci())
first_10 = [next(pipeline) for _ in range(10)]
print(f"\nFirst 10 processed Fibonacci: {first_10}")
# Memory comparison
import sys
eager_list = [x**2 for x in range(100000)]
lazy_gen = (x**2 for x in range(100000))
print(f"\nMemory usage:")
print(f" Eager list: {sys.getsizeof(eager_list):,} bytes")
print(f" Lazy generator: {sys.getsizeof(lazy_gen):,} bytes")Sequential map: 1.018s
First 10 processed Fibonacci: [0, 2, 32, 578, 10368, 186050, 3338528, 59907458, 1074995712, 19290015362]
Memory usage:
Eager list: 800,984 bytes
Lazy generator: 208 bytesPartial Functions and Currying
from functools import partial, reduce
import operator
# Partial function application
def power(base, exponent):
return base ** exponent
# Create specialized functions
square = partial(power, exponent=2)
cube = partial(power, exponent=3)
two_to_power = partial(power, base=2) # 2^x
print("Partial functions:")
print(f" square(5) = {square(5)}")
print(f" cube(5) = {cube(5)}")
print(f" 2^10 = {two_to_power(exponent=10)}")
# Partial with multiple arguments
def integrate(func, lower, upper, method='trapezoid', n_points=100):
"""Numerical integration."""
x = np.linspace(lower, upper, n_points)
y = func(x)
if method == 'trapezoid':
return np.trapz(y, x)
elif method == 'simpson':
from scipy.integrate import simpson
return simpson(y, x)
else:
raise ValueError(f"Unknown method: {method}")
# Create specialized integrators
simpson_integrate = partial(integrate, method='simpson')
unit_integrate = partial(integrate, lower=0, upper=1)
precise_integrate = partial(integrate, n_points=1000)
# Use specialized versions
result1 = simpson_integrate(np.sin, 0, np.pi)
result2 = unit_integrate(lambda x: x**2)
result3 = precise_integrate(np.exp, 0, 1)
print(f"\nIntegration results:")
print(f" ∫sin(x)dx [0,π] = {result1:.4f}")
print(f" ∫x²dx [0,1] = {result2:.4f}")
print(f" ∫e^x dx [0,1] = {result3:.4f}")Partial functions:
square(5) = 25
cube(5) = 125
2^10 = 1024
Integration results:
∫sin(x)dx [0,π] = 2.0000
∫x²dx [0,1] = 0.3334
∫e^x dx [0,1] = 1.7183functools.partial use cases:
- Pre-filling arguments for callbacks
- Creating specialized versions of general functions
- Configuration injection (default parameters)
# Common pattern: create specialized functions
from functools import partial
# Pre-configured logger
debug_log = partial(print, "[DEBUG]")
error_log = partial(print, "[ERROR]")
# Pre-configured numerical operations
normalize = partial(np.divide, b=255.0)
clip_unit = partial(np.clip, a_min=0, a_max=1)Currying (sequential application) is less common in Python than in functional languages. Use partial instead — it’s explicit and readable.
Composition pattern:
Decorators for Instrumentation
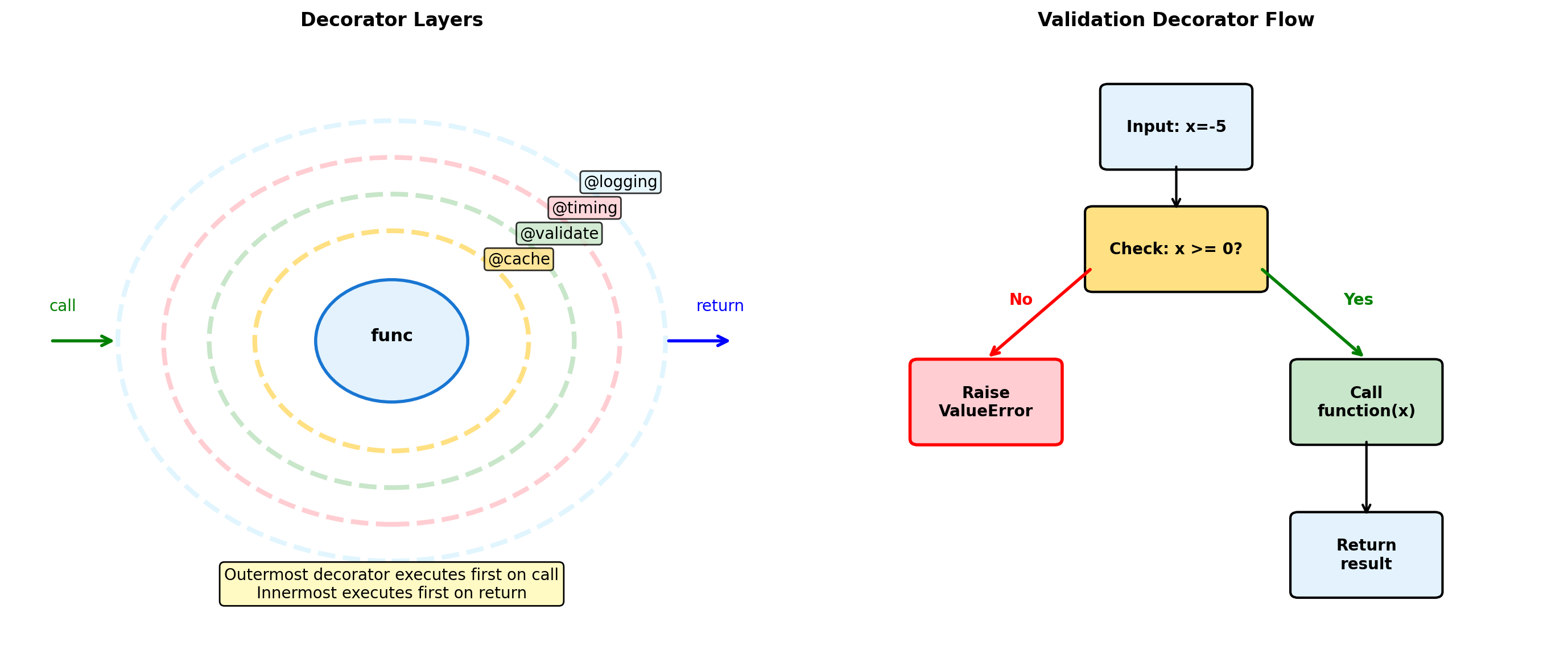
import time
import functools
def timer(func):
"""Simple timing decorator."""
@functools.wraps(func)
def wrapper(*args, **kwargs):
start = time.perf_counter()
result = func(*args, **kwargs)
elapsed = time.perf_counter() - start
print(f"{func.__name__} took {elapsed:.4f}s")
return result
return wrapper
@timer
def compute_sum(n):
"""Sum integers from 0 to n."""
return sum(range(n))
# Use decorated function
result = compute_sum(1000000)
print(f"Result: {result}")
# Decorator with arguments (decorator factory)
def repeat(n_times):
"""Decorator factory: repeat function call."""
def decorator(func):
@functools.wraps(func)
def wrapper(*args, **kwargs):
results = []
for _ in range(n_times):
results.append(func(*args, **kwargs))
return results
return wrapper
return decorator
@repeat(3)
def random_number():
import random
return random.random()
print(f"\nThree random numbers: {random_number()}")compute_sum took 0.0062s
Result: 499999500000
Three random numbers: [0.5372200917948131, 0.49622539930553966, 0.8577245806536437]Decorator pattern:
Use functools.wraps to preserve the original function’s metadata (__name__, __doc__).
Common decorator uses:
- Timing/profiling
- Logging
- Caching (
@functools.lru_cache) - Validation
- Authentication/authorization
Decorator factory (decorator with arguments):
@factory(arg) # factory(arg) returns decorator
def func():
pass
# Equivalent to:
func = factory(arg)(func)Stacking decorators:
SciPy: Compiled Libraries for Numerical Computing
SciPy Architecture: Python Interface to Fortran/C Libraries
SciPy provides Python bindings to decades of optimized numerical code.
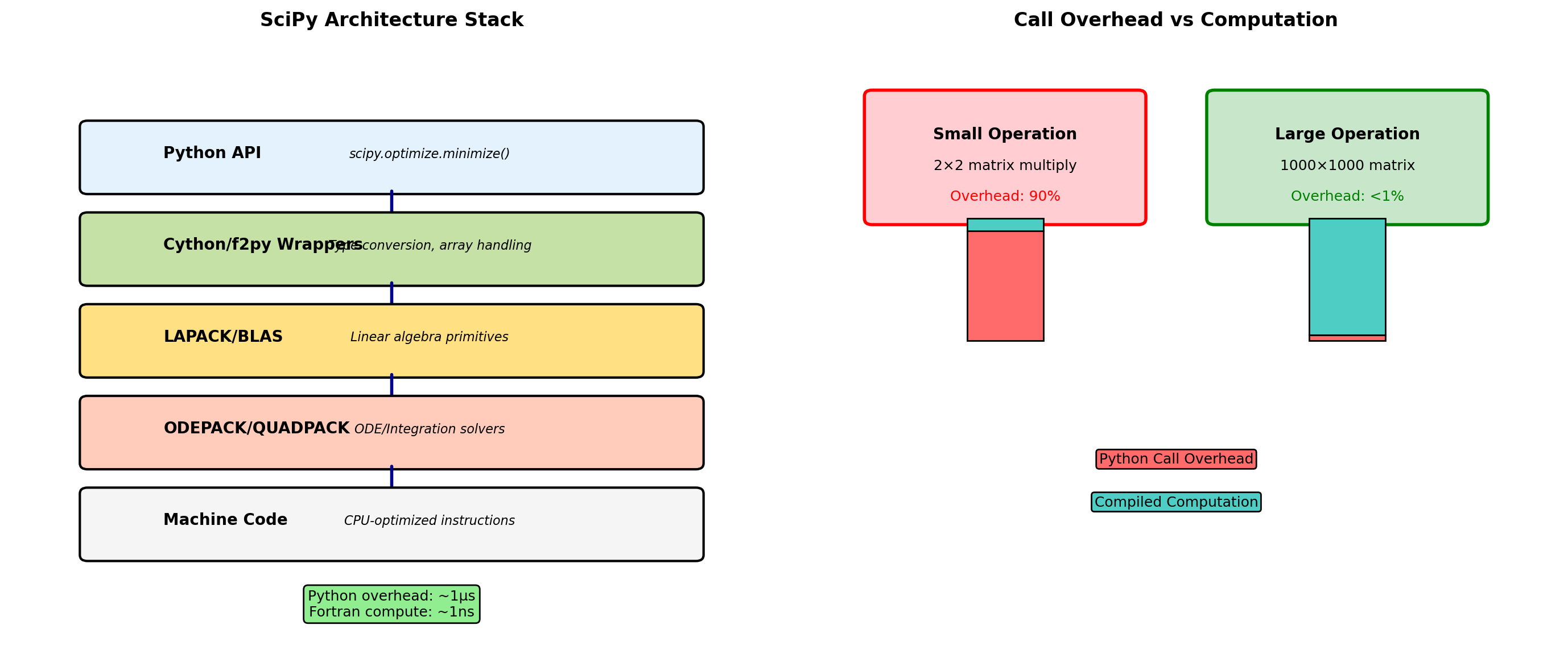
import scipy
import numpy as np
import timeit
# Demonstrate overhead vs computation
def small_operation():
"""Python function call dominates."""
A = np.array([[1, 2], [3, 4]])
return scipy.linalg.inv(A)
def large_operation():
"""Fortran computation dominates."""
A = np.random.randn(1000, 1000)
return scipy.linalg.inv(A)
# Measure call overhead
empty_call = timeit.timeit(lambda: None, number=100000)
print(f"Python function call: {empty_call*10:.2f}μs")
# Small vs large operation efficiency
A_small = np.random.randn(2, 2)
A_large = np.random.randn(100, 100)
t_small = timeit.timeit(
lambda: scipy.linalg.inv(A_small),
number=10000
)
t_large = timeit.timeit(
lambda: scipy.linalg.inv(A_large),
number=100
)
print(f"\n2×2 inversion: {t_small/10:.1f}μs per call")
print(f"100×100 inversion: {t_large*10:.1f}ms per call")
# BLAS level comparison
flops_small = 2**3 # O(n³) for inversion
flops_large = 100**3
print(f"\nFLOPS ratio: {flops_large/flops_small:,.0f}×")
print(f"Time ratio: {(t_large/100)/(t_small/10000):.0f}×")
print(f"Efficiency gain: {(flops_large/flops_small)/((t_large/100)/(t_small/10000)):.1f}×")Python function call: 0.01μs
2×2 inversion: 0.0μs per call
100×100 inversion: 1.0ms per call
FLOPS ratio: 125,000×
Time ratio: 230×
Efficiency gain: 542.3×Design Implications:
Wrapper overhead is constant - Same Python call cost regardless of problem size
Amortization strategy - Process vectors/matrices, not scalars
Library selection hierarchy:
- Intel MKL (commercial, fastest)
- OpenBLAS (open source, competitive)
- Reference BLAS (portable, slow)
Memory layout matters - Fortran order (column-major) vs C order (row-major)
Optimization: Interior Point vs Simplex Methods
Different algorithms excel at different problem structures.
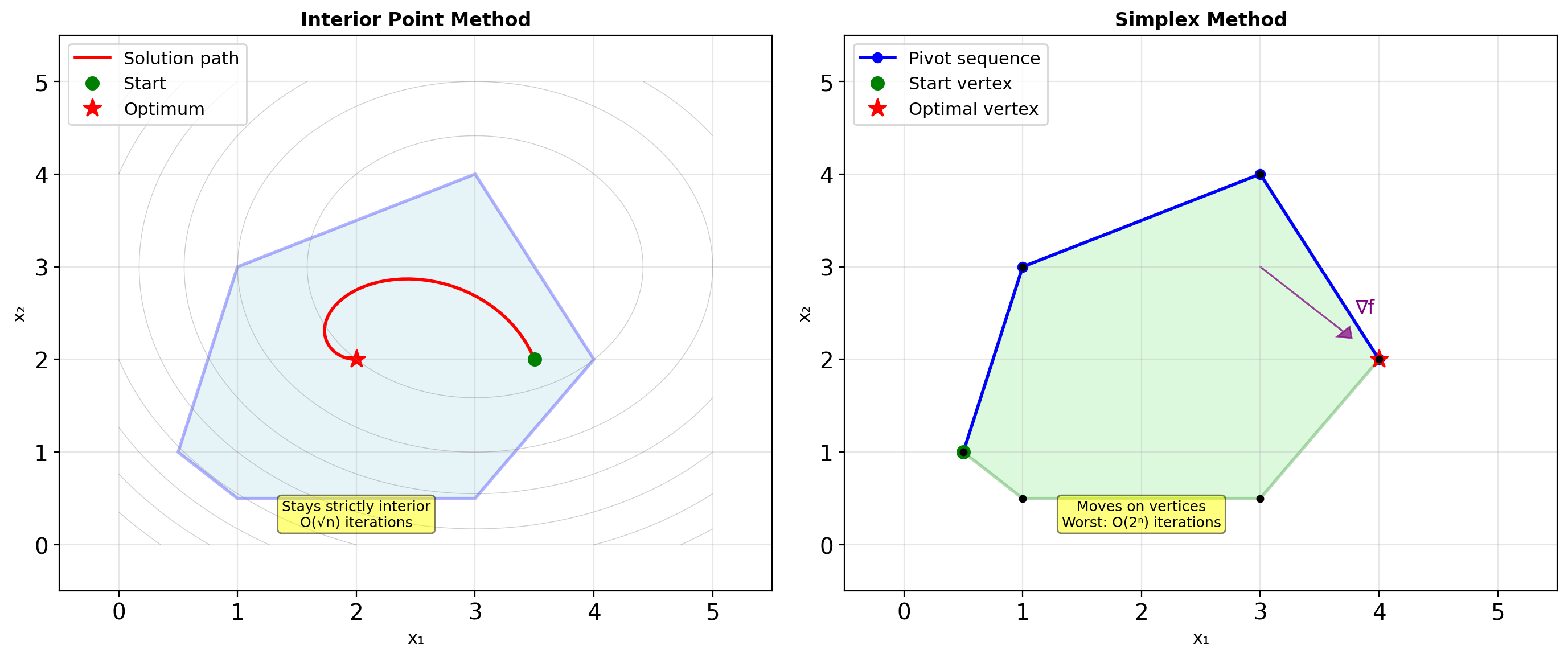
from scipy.optimize import linprog
import numpy as np
# Linear programming problem:
# minimize: -x - 2y
# subject to: x + 2y <= 8
# 2x + y <= 8
# x, y >= 0
c = [-1, -2] # Coefficients (minimize)
A_ub = [[1, 2], [2, 1]] # Inequality constraints
b_ub = [8, 8]
bounds = [(0, None), (0, None)]
# Compare methods
methods = ['interior-point', 'simplex', 'highs']
for method in methods:
result = linprog(c, A_ub=A_ub, b_ub=b_ub,
bounds=bounds, method=method)
print(f"{method:15s}: x={result.x}, "
f"iterations={result.nit}")
# Performance characteristics
n_vars = [10, 100, 1000]
for n in n_vars:
# Random LP problem
c = np.random.randn(n)
A = np.random.randn(n//2, n)
b = np.random.randn(n//2)
import time
# Interior point
start = time.perf_counter()
res_ip = linprog(c, A_ub=A, b_ub=b,
method='interior-point',
options={'disp': False})
time_ip = time.perf_counter() - start
# Simplex
start = time.perf_counter()
res_simplex = linprog(c, A_ub=A, b_ub=b,
method='simplex',
options={'disp': False})
time_simplex = time.perf_counter() - start
print(f"\nn={n:4d} variables:")
print(f" Interior: {time_ip*1000:6.1f}ms")
print(f" Simplex: {time_simplex*1000:6.1f}ms")interior-point : x=[1.6959609 3.15201955], iterations=4
simplex : x=[2.66666667 2.66666667], iterations=2
highs : x=[0. 4.], iterations=2
n= 10 variables:
Interior: 1.1ms
Simplex: 1.1ms
n= 100 variables:
Interior: 16.2ms
Simplex: 20.9ms
n=1000 variables:
Interior: 72.2ms
Simplex: 1038.5msAlgorithm Selection Criteria:
Interior Point:
- Polynomial worst-case: O(n³·⁵)
- Better for large, dense problems
- Generates strictly feasible iterates
- Smooth convergence profile
Simplex:
- Exponential worst-case, excellent average-case
- Superior for sparse problems
- Always at a vertex (basic feasible solution)
- Can exploit problem structure
Modern hybrids (HiGHS):
- Crossover between methods
- Presolver eliminates variables
- Parallel execution paths
Root Finding: Convergence Rates and Stability
Root finding methods trade convergence speed for robustness.
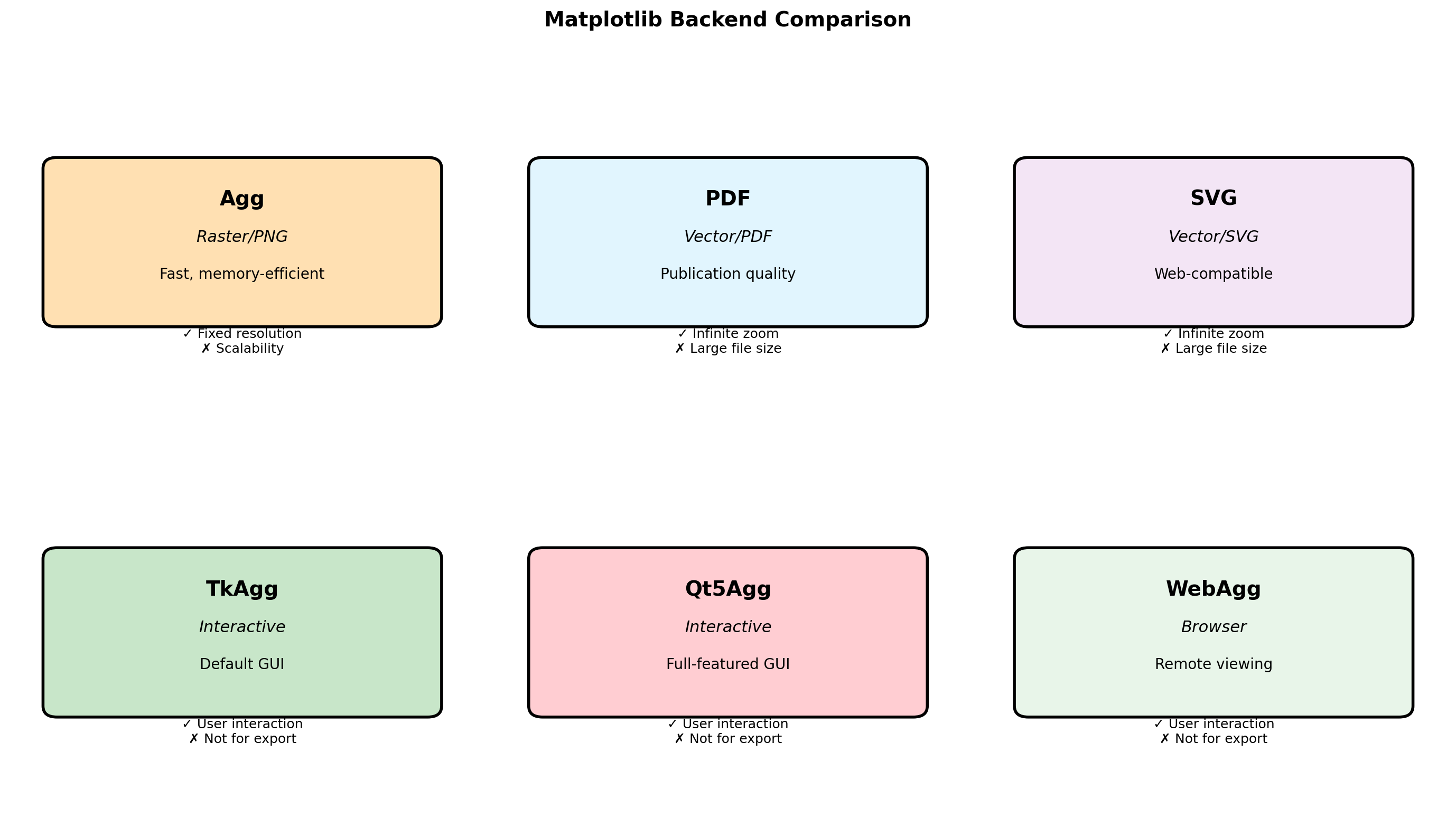
from scipy import optimize
import numpy as np
def f(x):
"""Test function with known root."""
return x**3 - x - 1
def fprime(x):
"""Derivative of f."""
return 3*x**2 - 1
# Compare root finding methods
x0 = 2.0 # Initial guess
bracket = [1, 2] # Known bracket
# Bisection: guaranteed convergence
root_bisect = optimize.bisect(f, *bracket)
print(f"Bisection: {root_bisect:.10f}")
# Brent: combines bisection, secant, inverse quadratic
root_brent = optimize.brentq(f, *bracket)
print(f"Brent: {root_brent:.10f}")
# Newton: fast but needs derivative
root_newton = optimize.newton(f, x0, fprime=fprime)
print(f"Newton: {root_newton:.10f}")
# Performance comparison
import timeit
n = 1000
times = {}
times['bisect'] = timeit.timeit(
lambda: optimize.bisect(f, 1, 2),
number=n
)
times['brent'] = timeit.timeit(
lambda: optimize.brentq(f, 1, 2),
number=n
)
times['newton'] = timeit.timeit(
lambda: optimize.newton(f, 2.0, fprime=fprime),
number=n
)
print(f"\nTime for {n} root findings:")
for method, time in times.items():
print(f" {method:8s}: {time*1000:.1f}ms")Bisection: 1.3247179572
Brent: 1.3247179572
Newton: 1.3247179572
Time for 1000 root findings:
bisect : 20.7ms
brent : 6.0ms
newton : 57.5msMethod Characteristics:
Bisection:
- Requires bracket [a, b] where f(a)·f(b) < 0
- Guaranteed convergence
- Linear rate: log₂(ε₀/ε) iterations
- One function evaluation per iteration
Newton-Raphson:
- Requires derivative
- Quadratic convergence near root
- Can diverge or cycle
- Two evaluations per iteration (f and f’)
Brent’s Method (scipy default):
- Hybrid: bisection + secant + inverse quadratic
- Guaranteed convergence with bracket
- Superlinear convergence in practice
- Adaptive algorithm selection
Numerical Integration: Adaptive Quadrature
Integration routines balance function evaluations against accuracy.
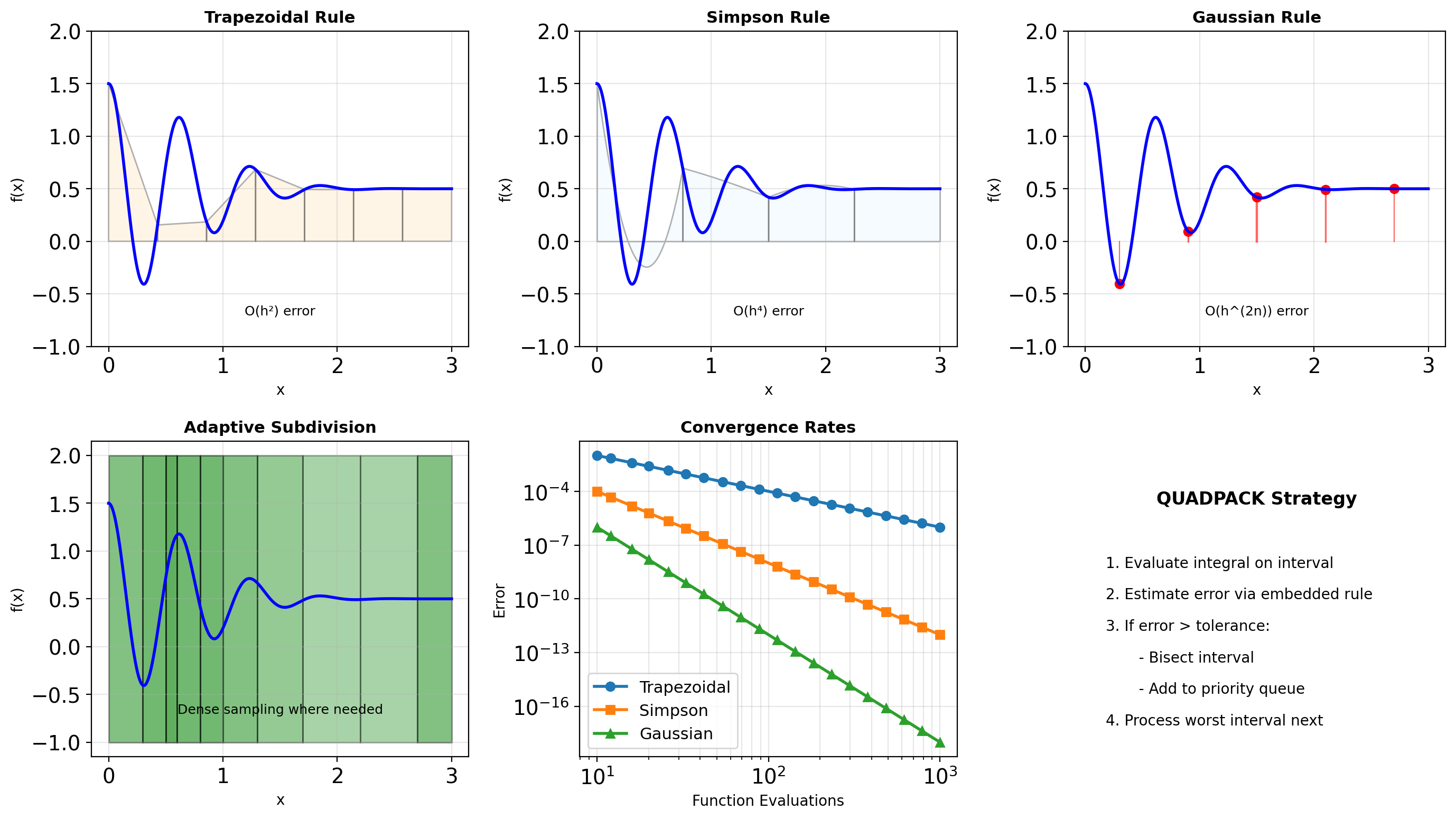
from scipy import integrate
import numpy as np
def oscillatory(x):
"""Challenging integrand."""
return np.exp(-x**2) * np.cos(10*x)
# Basic integration
result, error = integrate.quad(oscillatory, 0, 3)
print(f"quad result: {result:.8f} ± {error:.2e}")
# Show function evaluation count
full_output = integrate.quad(oscillatory, 0, 3,
full_output=True)
result, error, info = full_output
print(f"Function evaluations: {info['neval']}")
# Compare tolerances
tolerances = [1e-3, 1e-6, 1e-9]
for tol in tolerances:
result, error, info = integrate.quad(
oscillatory, 0, 3,
epsabs=tol, full_output=True
)
print(f"tol={tol:.0e}: {info['neval']:3d} evals, "
f"error={error:.2e}")
# Fixed vs adaptive sampling
def fixed_trapezoid(f, a, b, n):
"""Fixed spacing trapezoid rule."""
x = np.linspace(a, b, n)
y = f(x)
return np.trapz(y, x)
n_fixed = 1000
result_fixed = fixed_trapezoid(oscillatory, 0, 3, n_fixed)
result_adaptive, _, info = integrate.quad(
oscillatory, 0, 3, full_output=True
)
print(f"\nFixed {n_fixed} points: {result_fixed:.6f}")
print(f"Adaptive {info['neval']} points: {result_adaptive:.6f}")quad result: -0.00000982 ± 6.48e-15
Function evaluations: 147
tol=1e-03: 63 evals, error=4.38e-06
tol=1e-06: 105 evals, error=9.08e-08
tol=1e-09: 147 evals, error=6.48e-15
Fixed 1000 points: -0.000010
Adaptive 147 points: -0.000010QUADPACK Algorithms (scipy.integrate):
quad (adaptive quadrature):
- Gauss-Kronrod 21-point rule
- Error estimate from embedded 10-point rule
- Bisects intervals exceeding tolerance
- Globally adaptive strategy
Performance Factors:
- Smoothness: Higher derivatives → faster convergence
- Oscillations: Require subdivision
- Singularities: Special handling needed
- Dimensionality: Curse affects all methods
Specialized Routines:
quad_vec: Vectorized integrandsnquad: Multiple integrationdblquad,tplquad: 2D/3D convenienceodeint: ODE integration
Sparse Matrices: Storage Formats
Sparse matrices store only non-zero elements, trading format complexity for memory efficiency.
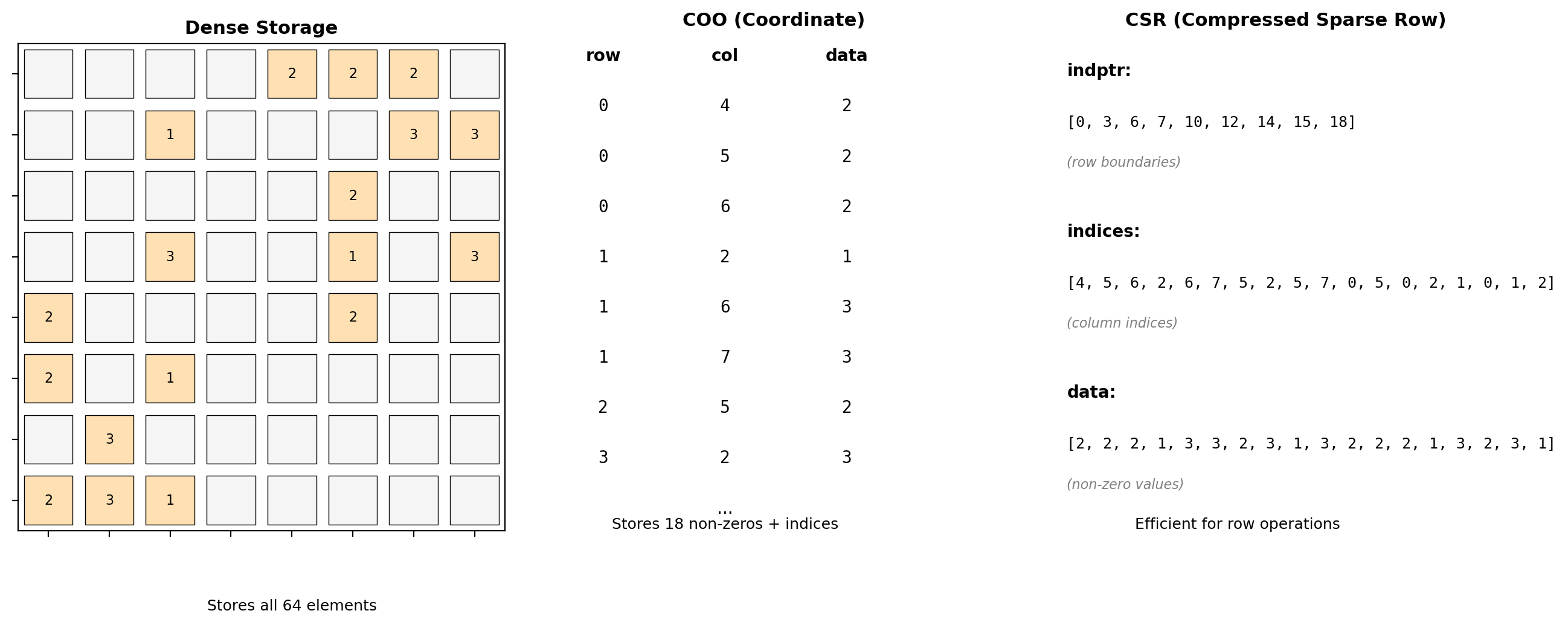
Format Selection
- COO: Best for construction and adding entries
- CSR: Best for row slicing and matrix-vector products
- CSC: Best for column slicing and linear solvers
import scipy.sparse as sp
import numpy as np
# Create sparse matrix
n = 1000
density = 0.01
A_dense = sp.rand(n, n, density=density, format='dense')
A_dense = np.array(A_dense)
# Convert to different formats
A_coo = sp.coo_matrix(A_dense)
A_csr = sp.csr_matrix(A_dense)
A_csc = sp.csc_matrix(A_dense)
# Memory usage
import sys
dense_size = sys.getsizeof(A_dense) / 1024**2
coo_size = (A_coo.data.nbytes +
A_coo.row.nbytes +
A_coo.col.nbytes) / 1024**2
csr_size = (A_csr.data.nbytes +
A_csr.indices.nbytes +
A_csr.indptr.nbytes) / 1024**2
print(f"Matrix {n}×{n}, density {density:.1%}")
print(f"Dense: {dense_size:.2f} MB")
print(f"COO: {coo_size:.2f} MB ({dense_size/coo_size:.1f}× smaller)")
print(f"CSR: {csr_size:.2f} MB ({dense_size/csr_size:.1f}× smaller)")
# Operation performance
v = np.random.randn(n)
import timeit
t_dense = timeit.timeit(lambda: A_dense @ v, number=100)
t_csr = timeit.timeit(lambda: A_csr @ v, number=100)
print(f"\nMatrix-vector multiply (100 iterations):")
print(f"Dense: {t_dense*1000:.1f}ms")
print(f"CSR: {t_csr*1000:.1f}ms ({t_dense/t_csr:.1f}× faster)")
# Format conversion cost
t_to_csr = timeit.timeit(
lambda: sp.csr_matrix(A_dense),
number=10
)
print(f"\nConversion to CSR: {t_to_csr*100:.1f}ms")Matrix 1000×1000, density 1.0%
Dense: 7.63 MB
COO: 0.15 MB (50.0× smaller)
CSR: 0.12 MB (64.5× smaller)
Matrix-vector multiply (100 iterations):
Dense: 7.1ms
CSR: 1.2ms (5.8× faster)
Conversion to CSR: 4.2msStorage Format Trade-offs:
COO (Coordinate):
- Three arrays: (row, col, data)
- No sorting required
- Allows duplicates (summed on conversion)
- Inefficient for arithmetic
CSR/CSC (Compressed Sparse Row/Column):
- Row-wise: (indptr, indices, data)
- Efficient row/column access
- Fast matrix-vector products
- Standard solver format
Performance Implications:
- Dense wins below ~10% density
- Format conversion has significant cost
- Row vs column access patterns matter
- In-place operations often impossible
Data Visualization with Matplotlib
Matplotlib Architecture: Object Hierarchy
Matplotlib uses a hierarchical object model that separates concerns across multiple abstraction levels.
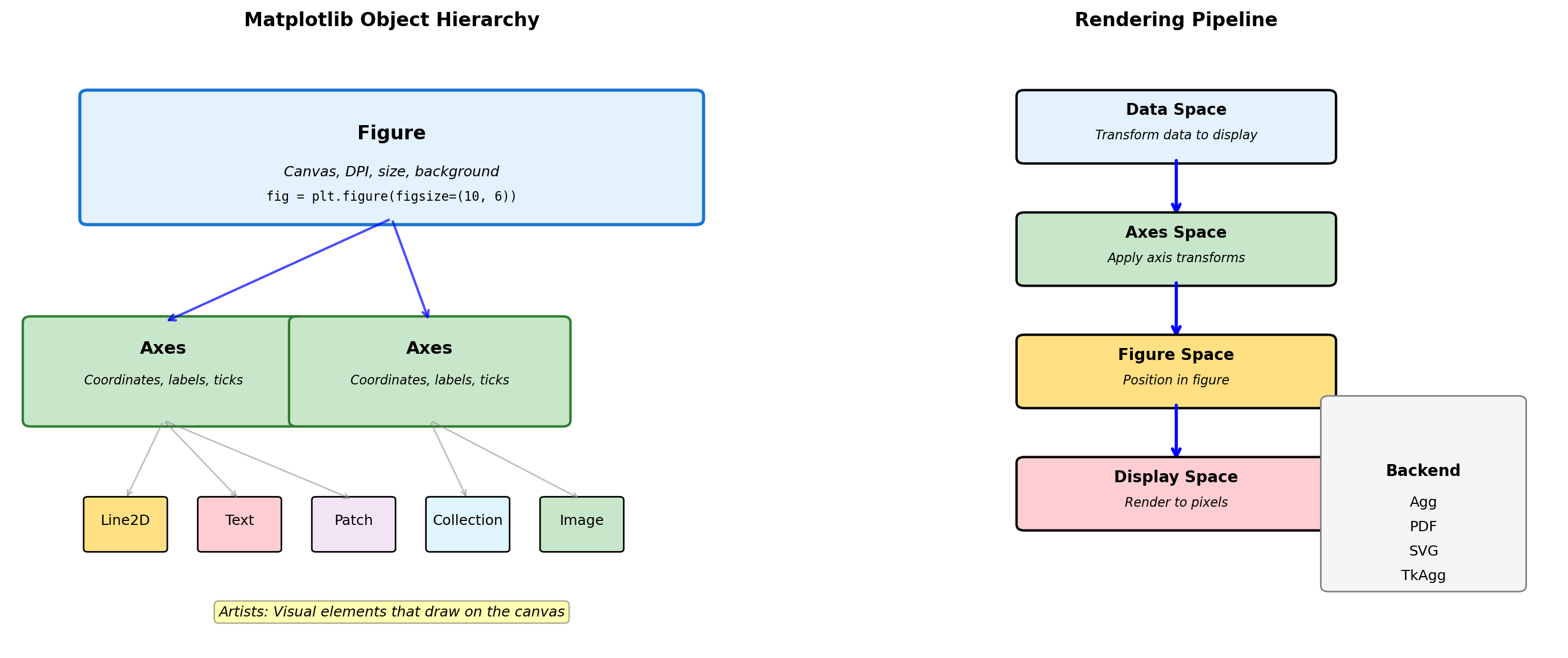
import matplotlib.pyplot as plt
import matplotlib as mpl
# Examine object hierarchy
fig = plt.figure(figsize=(8, 4))
ax1 = fig.add_subplot(121)
ax2 = fig.add_subplot(122)
# Plot creates multiple artists
line, = ax1.plot([1, 2, 3], [1, 4, 2], 'b-')
scatter = ax2.scatter([1, 2, 3], [2, 3, 1])
# Object relationships
print("Figure attributes:")
print(f" Number of axes: {len(fig.axes)}")
print(f" DPI: {fig.dpi}")
print(f" Size: {fig.get_size_inches()} inches")
print("\nAxes ax1 contents:")
print(f" Lines: {len(ax1.lines)}")
print(f" Patches: {len(ax1.patches)}")
print(f" Texts: {len(ax1.texts)}")
print(f" Artists: {len(ax1.get_children())}")
# Access artist properties
print(f"\nLine2D properties:")
print(f" Data: x={line.get_xdata()}, y={line.get_ydata()}")
print(f" Color: {line.get_color()}")
print(f" Linewidth: {line.get_linewidth()}")
print(f" Marker: '{line.get_marker()}'")
# Transform pipeline
data_point = (2, 4)
display_point = ax1.transData.transform(data_point)
figure_point = fig.transFigure.inverted().transform(display_point)
print(f"\nTransform pipeline for {data_point}:")
print(f" Data space: {data_point}")
print(f" Display space: {display_point}")
print(f" Figure space: {figure_point}")
plt.close() # Clean upFigure attributes:
Number of axes: 2
DPI: 100.0
Size: [8. 4.] inches
Axes ax1 contents:
Lines: 1
Patches: 0
Texts: 0
Artists: 11
Line2D properties:
Data: x=[1 2 3], y=[1 4 2]
Color: b
Linewidth: 2.0
Marker: 'None'
Transform pipeline for (2, 4):
Data space: (2, 4)
Display space: [ 663.63636364 1276. ]
Figure space: [0.82954545 3.19 ]Architecture Components:
Figure: Top-level container
- Manages canvas and renderer
- Controls output size and DPI
- Contains one or more Axes
Axes: Plotting area with coordinates
- Data limits and scaling
- Tick locators and formatters
- Contains Artists
Artists: Everything visible
- Primitives: Line2D, Rectangle, Text
- Collections: LineCollection, PathCollection
- Containers: Axis, Legend
Transforms: Coordinate mappings
- Data → Axes → Figure → Display
- Enables zoom, pan, aspect ratio
Backend: Rendering engine
- Interactive: Qt5Agg, TkAgg
- Hardcopy: Agg, PDF, SVG
Plot Types for Scientific Data
Different visualizations optimize for different data characteristics and analysis goals.
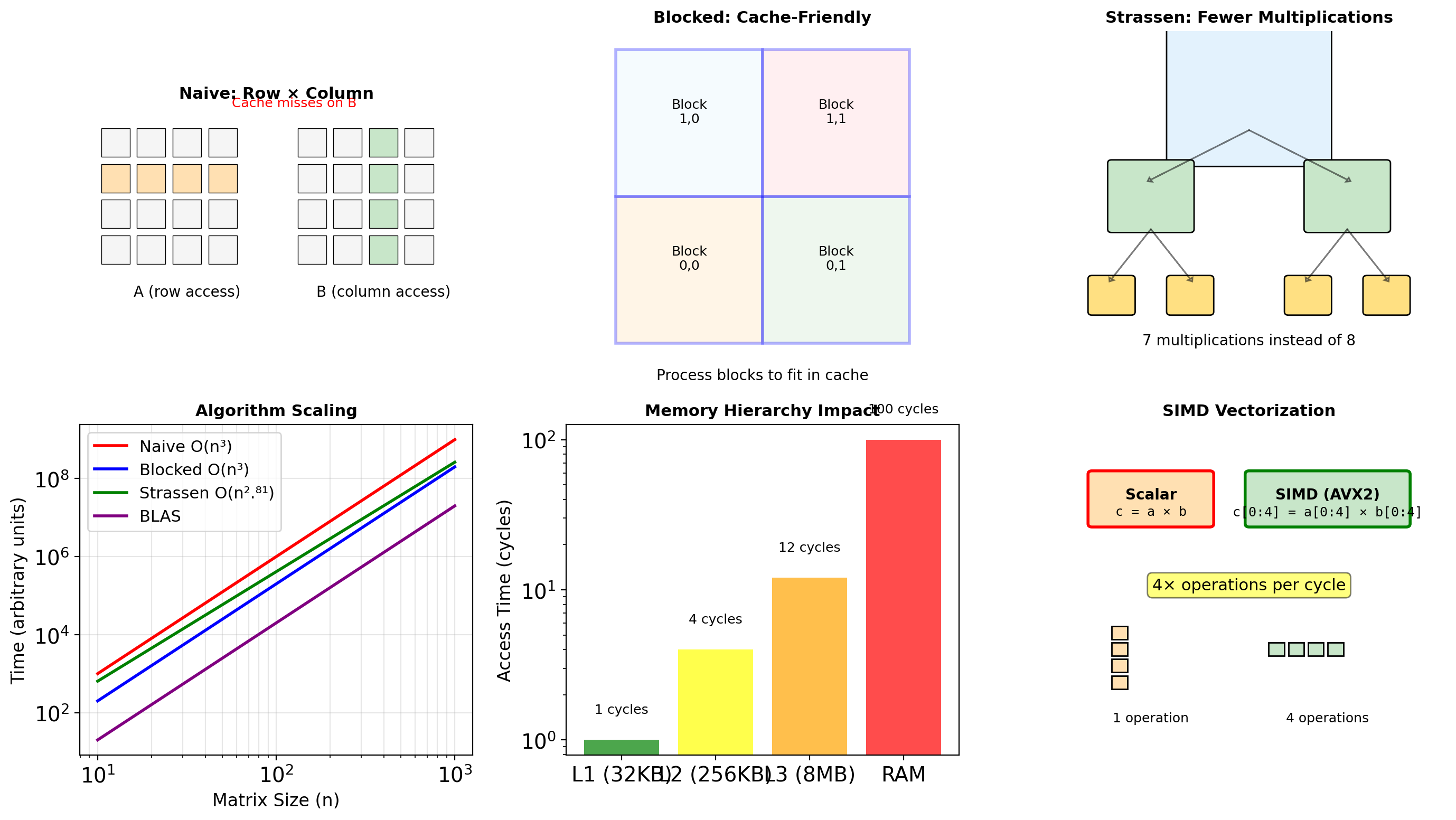
import matplotlib.pyplot as plt
import numpy as np
# Performance comparison for different plot types
data_sizes = [100, 1000, 10000, 100000]
plot_types = {
'line': lambda ax, n: ax.plot(np.arange(n), np.random.randn(n)),
'scatter': lambda ax, n: ax.scatter(np.arange(n), np.random.randn(n)),
'hist': lambda ax, n: ax.hist(np.random.randn(n), bins=50),
'imshow': lambda ax, n: ax.imshow(np.random.randn(int(np.sqrt(n)), int(np.sqrt(n)))),
}
import time
print("Rendering time (ms) for different plot types:")
print(f"{'Size':<10} {'Line':<10} {'Scatter':<10} {'Hist':<10} {'Imshow':<10}")
print("-" * 50)
for size in data_sizes:
times = {}
for plot_type, plot_func in plot_types.items():
fig, ax = plt.subplots()
start = time.perf_counter()
plot_func(ax, size)
fig.canvas.draw()
elapsed = (time.perf_counter() - start) * 1000
times[plot_type] = elapsed
plt.close(fig)
print(f"{size:<10} {times['line']:<10.1f} {times['scatter']:<10.1f} "
f"{times['hist']:<10.1f} {times['imshow']:<10.1f}")
# Memory usage analysis
import sys
fig, ax = plt.subplots()
line, = ax.plot(np.arange(10000), np.random.randn(10000))
scatter = ax.scatter(np.arange(1000), np.random.randn(1000))
print(f"\nMemory usage:")
print(f" Line (10k points): ~{sys.getsizeof(line.get_xydata()) / 1024:.1f} KB")
print(f" Scatter (1k points): ~{sys.getsizeof(scatter.get_offsets()) / 1024:.1f} KB")
plt.close()Rendering time (ms) for different plot types:
Size Line Scatter Hist Imshow
--------------------------------------------------
100 12.0 11.0 21.0 14.4
1000 16.4 11.7 21.4 15.8
10000 66.6 16.2 125.2 14.2
100000 311.6 48.6 23.7 20.0
Memory usage:
Line (10k points): ~156.4 KB
Scatter (1k points): ~0.2 KBPlot Selection Criteria:
Continuous Data:
- Line: Time series, functions
- Fill: Confidence intervals, ranges
- Contour: 2D scalar fields
Discrete Points:
- Scatter: Correlations, outliers
- Hexbin: Large datasets (>10k points)
- Histogram: Distributions
Statistical:
- Box: Quartiles and outliers
- Violin: Distribution shape
- Error bars: Measurement uncertainty
Performance Tips:
- Use
plot()overscatter()for large datasets - Rasterize dense plots:
rasterized=True - Downsample data before plotting
- Use blitting for animations
Subplot Layouts and Composition
Complex figures require careful layout management for effective visualization.
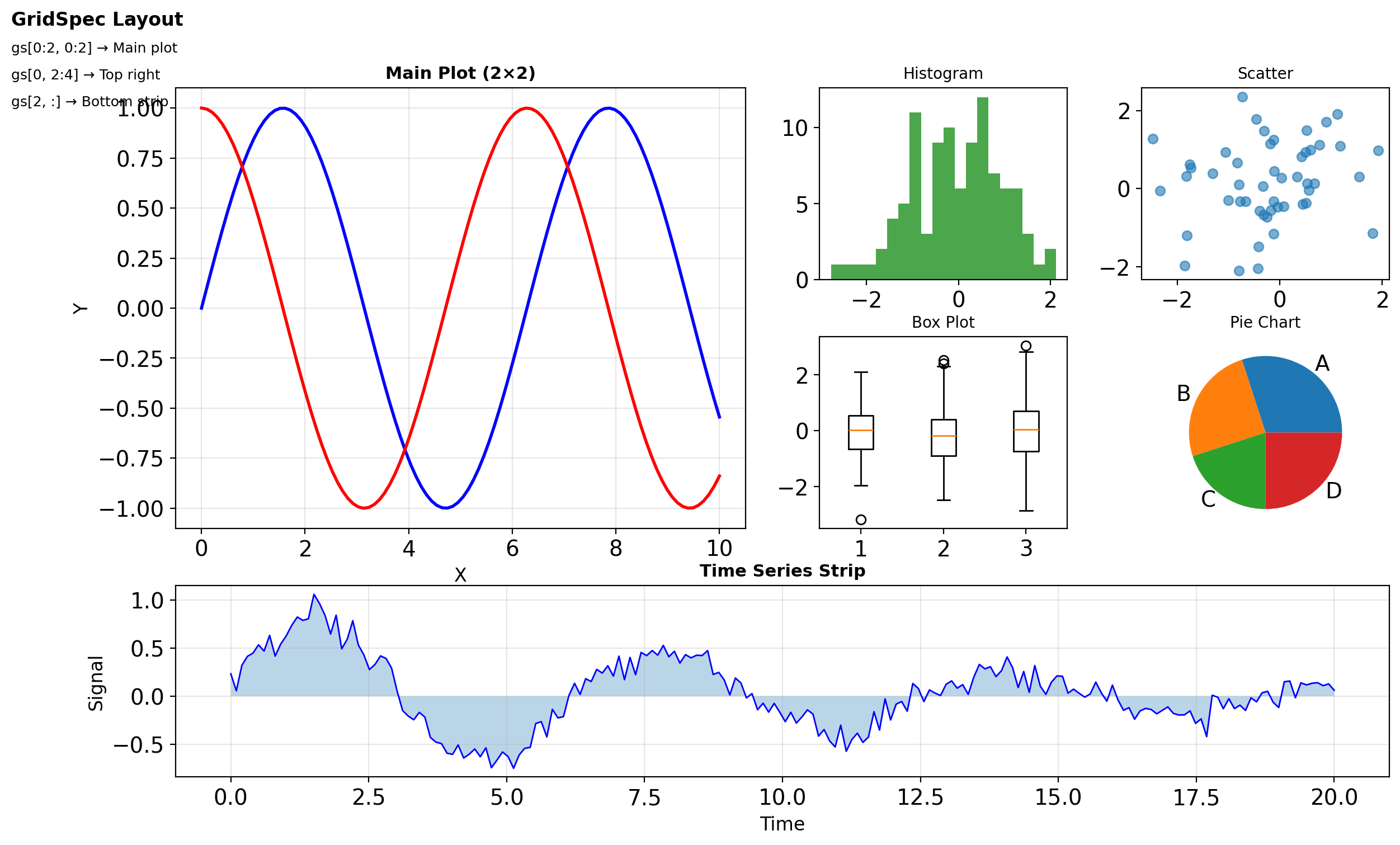
import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec
import numpy as np
# Method 1: Simple grid
fig1, axes = plt.subplots(2, 3, figsize=(9, 6))
print(f"Simple grid: {axes.shape} axes")
# Method 2: GridSpec for complex layouts
fig2 = plt.figure(figsize=(10, 6))
gs = gridspec.GridSpec(3, 3, figure=fig2,
width_ratios=[1, 2, 1],
height_ratios=[1, 2, 1],
hspace=0.3, wspace=0.3)
# Create axes with different spans
ax1 = fig2.add_subplot(gs[0, :]) # Top row, all columns
ax2 = fig2.add_subplot(gs[1:, 0]) # Rows 1-2, first column
ax3 = fig2.add_subplot(gs[1:, 1:]) # Rows 1-2, columns 1-2
print(f"\nGridSpec axes positions:")
print(f" ax1: {ax1.get_position()}")
print(f" ax2: {ax2.get_position()}")
print(f" ax3: {ax3.get_position()}")
# Method 3: Nested layouts
fig3 = plt.figure(figsize=(10, 6))
outer_grid = gridspec.GridSpec(2, 2, figure=fig3)
# Nested grid in first cell
inner_grid = gridspec.GridSpecFromSubplotSpec(
2, 2, subplot_spec=outer_grid[0, 0]
)
# Create nested axes
for i in range(2):
for j in range(2):
ax = fig3.add_subplot(inner_grid[i, j])
ax.text(0.5, 0.5, f'({i},{j})', ha='center')
# Regular axes in other cells
ax_right = fig3.add_subplot(outer_grid[0, 1])
ax_bottom = fig3.add_subplot(outer_grid[1, :])
plt.close('all') # Clean up
# Constrained layout for automatic spacing
fig4, axes = plt.subplots(2, 2, figsize=(8, 6),
constrained_layout=True)
for ax in axes.flat:
ax.plot(np.random.randn(100))
ax.set_title('Auto-spaced')
print("\nConstrained layout automatically adjusts spacing")
plt.close('all')Simple grid: (2, 3) axes
GridSpec axes positions:
ax1: Bbox(x0=0.125, y0=0.7195833333333334, x1=0.9000000000000001, y1=0.88)
ax2: Bbox(x0=0.125, y0=0.10999999999999999, x1=0.28645833333333337, y1=0.6554166666666668)
ax3: Bbox(x0=0.3510416666666667, y0=0.10999999999999999, x1=0.9000000000000001, y1=0.6554166666666668)
Constrained layout automatically adjusts spacing# Shared axes for comparison
fig, axes = plt.subplots(3, 1, figsize=(8, 6),
sharex=True)
x = np.linspace(0, 10, 100)
data = [np.sin(x), np.cos(x), np.sin(x) * np.cos(x)]
labels = ['sin(x)', 'cos(x)', 'sin(x)cos(x)']
for ax, y, label in zip(axes, data, labels):
ax.plot(x, y, linewidth=2)
ax.set_ylabel(label)
ax.grid(True, alpha=0.3)
# Only bottom axis shows x-label
if ax == axes[-1]:
ax.set_xlabel('X')
axes[0].set_title('Shared X-axis', fontweight='bold')
# Measure rendering overhead
import time
layout_times = {}
# Simple layout
start = time.perf_counter()
fig, axes = plt.subplots(3, 3)
fig.canvas.draw()
layout_times['simple'] = time.perf_counter() - start
# Complex GridSpec
start = time.perf_counter()
fig = plt.figure()
gs = gridspec.GridSpec(5, 5)
for i in range(5):
for j in range(5):
ax = fig.add_subplot(gs[i, j])
fig.canvas.draw()
layout_times['complex'] = time.perf_counter() - start
print("\nLayout creation overhead:")
for layout, t in layout_times.items():
print(f" {layout}: {t*1000:.1f}ms")
plt.close('all')
Layout creation overhead:
simple: 78.2ms
complex: 145.9ms3D Visualization
Three-dimensional plots require special consideration for perspective and interaction.
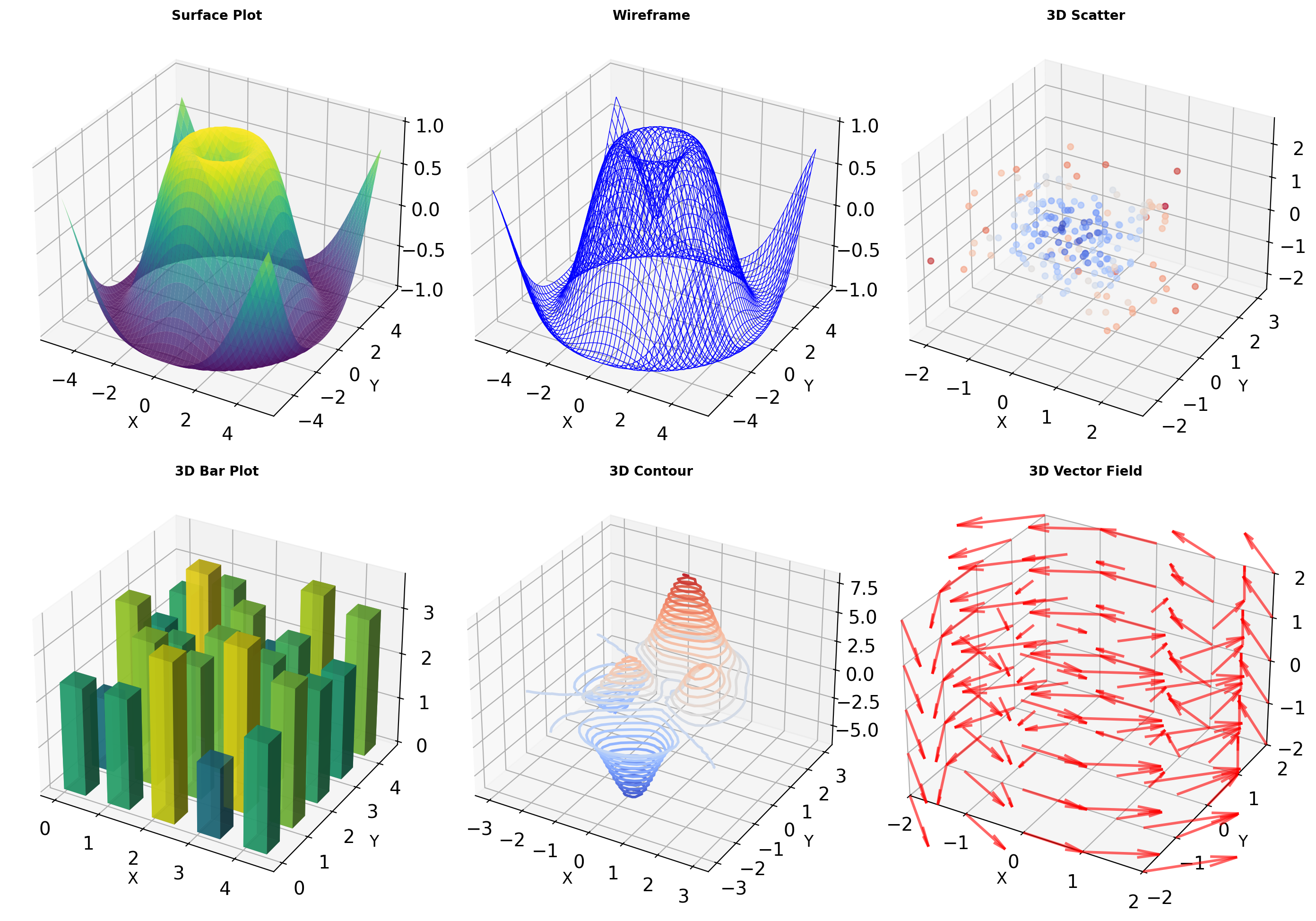
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
import time
# Performance analysis for 3D plots
fig = plt.figure(figsize=(10, 5))
# Compare 2D vs 3D rendering
grid_sizes = [10, 20, 30, 40, 50]
times_2d = []
times_3d = []
for size in grid_sizes:
X = np.linspace(-5, 5, size)
Y = np.linspace(-5, 5, size)
X, Y = np.meshgrid(X, Y)
Z = np.sin(np.sqrt(X**2 + Y**2))
# 2D heatmap
fig2d, ax2d = plt.subplots()
start = time.perf_counter()
ax2d.imshow(Z)
fig2d.canvas.draw()
times_2d.append(time.perf_counter() - start)
plt.close(fig2d)
# 3D surface
fig3d = plt.figure()
ax3d = fig3d.add_subplot(111, projection='3d')
start = time.perf_counter()
ax3d.plot_surface(X, Y, Z)
fig3d.canvas.draw()
times_3d.append(time.perf_counter() - start)
plt.close(fig3d)
print("Rendering time comparison (ms):")
print(f"{'Grid':<10} {'2D Heatmap':<15} {'3D Surface':<15} {'Ratio':<10}")
print("-" * 50)
for i, size in enumerate(grid_sizes):
ratio = times_3d[i] / times_2d[i]
print(f"{size}×{size:<6} {times_2d[i]*1000:<15.1f} "
f"{times_3d[i]*1000:<15.1f} {ratio:<10.1f}x")
# View angle impact
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
# Create surface
X = np.linspace(-5, 5, 30)
Y = np.linspace(-5, 5, 30)
X, Y = np.meshgrid(X, Y)
Z = np.sin(np.sqrt(X**2 + Y**2))
ax.plot_surface(X, Y, Z, cmap='viridis')
# Get view angles
elev = ax.elev
azim = ax.azim
print(f"\nDefault view angles:")
print(f" Elevation: {elev}°")
print(f" Azimuth: {azim}°")
# Programmatic rotation
ax.view_init(elev=30, azim=45)
print(f"Modified view: elev=30°, azim=45°")
plt.close()Rendering time comparison (ms):
Grid 2D Heatmap 3D Surface Ratio
--------------------------------------------------
10×10 14.2 19.5 1.4 x
20×20 16.9 26.7 1.6 x
30×30 14.8 37.2 2.5 x
40×40 16.5 50.9 3.1 x
50×50 13.0 76.1 5.8 x
Default view angles:
Elevation: 30°
Azimuth: -60°
Modified view: elev=30°, azim=45°<Figure size 1000x500 with 0 Axes># 3D plotting optimizations
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
# Optimization strategies
fig = plt.figure(figsize=(8, 4))
# Strategy 1: Reduce resolution
ax1 = fig.add_subplot(121, projection='3d')
X_low = np.linspace(-5, 5, 20) # Low resolution
Y_low = np.linspace(-5, 5, 20)
X_low, Y_low = np.meshgrid(X_low, Y_low)
Z_low = np.sin(np.sqrt(X_low**2 + Y_low**2))
ax1.plot_surface(X_low, Y_low, Z_low,
cmap='viridis', alpha=0.8)
ax1.set_title('Low Resolution (Fast)')
# Strategy 2: Use simpler representations
ax2 = fig.add_subplot(122, projection='3d')
ax2.plot_wireframe(X_low, Y_low, Z_low,
color='blue', linewidth=0.5,
rstride=2, cstride=2) # Skip points
ax2.set_title('Wireframe (Faster)')
# Memory usage
import sys
surf_artist = ax1.collections[0]
wire_artist = ax2.collections[0]
print("\nMemory comparison:")
print(f" Surface plot: ~{len(surf_artist._facecolors)*4/1024:.1f} KB")
print(f" Wireframe: ~{len(wire_artist._segments3d)*24/1024:.1f} KB")
# Z-order sorting overhead
n_triangles = X_low.size * 2 # Approximate
print(f"\nZ-buffer sorting:")
print(f" Triangles to sort: ~{n_triangles}")
print(f" Complexity: O(n log n) = O({n_triangles} log {n_triangles})")
plt.tight_layout()
plt.close()
# Interactive considerations
print("\n3D interaction overhead:")
print(" Mouse rotation: Recomputes projections")
print(" Zoom: Recalculates clipping")
print(" Pan: Updates transform matrices")
Memory comparison:
Surface plot: ~0.0 KB
Wireframe: ~0.5 KB
Z-buffer sorting:
Triangles to sort: ~800
Complexity: O(n log n) = O(800 log 800)
3D interaction overhead:
Mouse rotation: Recomputes projections
Zoom: Recalculates clipping
Pan: Updates transform matricesAnimations for Time Series
Animations visualize temporal evolution but require careful performance optimization.
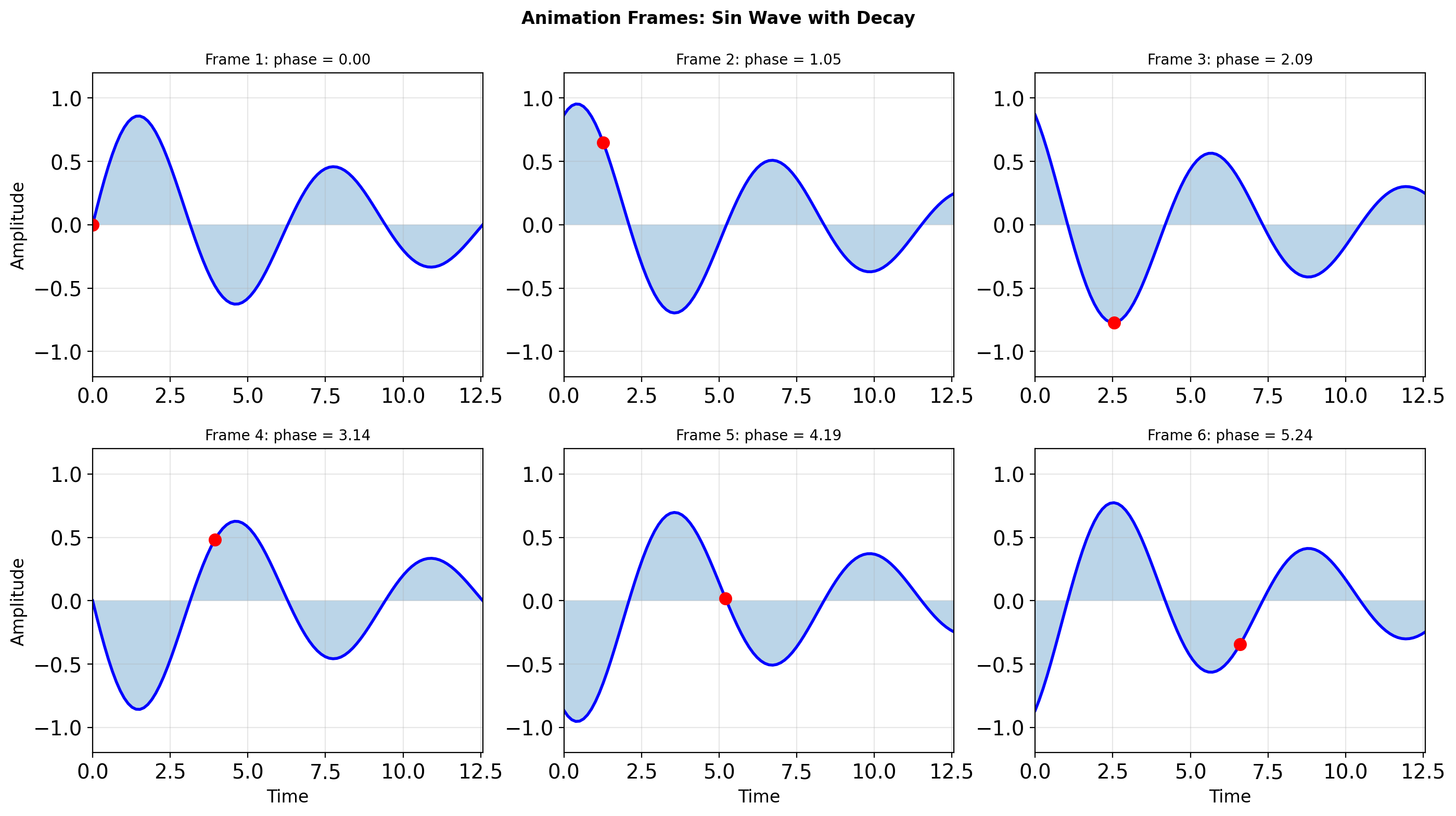
import matplotlib.pyplot as plt
import matplotlib.animation as animation
import numpy as np
# Basic animation structure
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(8, 6))
# Data setup
x = np.linspace(0, 2*np.pi, 100)
line1, = ax1.plot([], [], 'b-', linewidth=2)
line2, = ax2.plot([], [], 'r-', linewidth=2)
ax1.set_xlim(0, 2*np.pi)
ax1.set_ylim(-1.5, 1.5)
ax1.set_title('Animation with Blitting')
ax1.grid(True, alpha=0.3)
ax2.set_xlim(0, 2*np.pi)
ax2.set_ylim(-1.5, 1.5)
ax2.set_title('Accumulated History')
ax2.grid(True, alpha=0.3)
# Animation state
history = []
def init():
"""Initialize animation."""
line1.set_data([], [])
line2.set_data([], [])
return line1, line2
def animate(frame):
"""Animation function called for each frame."""
# Update data
y1 = np.sin(x + frame * 0.1)
line1.set_data(x, y1)
# Accumulate history
if len(history) > 50:
history.pop(0)
history.append(np.sin(2*np.pi * frame / 50))
# Plot history
if history:
line2.set_data(np.linspace(0, 2*np.pi, len(history)),
history)
return line1, line2
# Performance comparison
import time
# Without blitting
start = time.perf_counter()
for i in range(50):
animate(i)
fig.canvas.draw()
no_blit_time = time.perf_counter() - start
print(f"Animation performance (50 frames):")
print(f" Without blitting: {no_blit_time*1000:.1f}ms")
print(f" FPS: {50/no_blit_time:.1f}")
# Memory management
print(f"\nMemory considerations:")
print(f" Line data: {x.nbytes + x.nbytes} bytes per frame")
print(f" History buffer: {len(history) * 8} bytes")
print(f" Canvas cache: ~{fig.canvas.get_width_height()[0] * fig.canvas.get_width_height()[1] * 4} bytes")
plt.close()
# Optimization techniques
print("\nOptimization strategies:")
print(" 1. Use blitting: ~5-10x speedup")
print(" 2. Update only changed artists")
print(" 3. Reduce figure DPI for preview")
print(" 4. Cache static elements")
print(" 5. Use collections for many objects")Animation performance (50 frames):
Without blitting: 539.8ms
FPS: 92.6
Memory considerations:
Line data: 1600 bytes per frame
History buffer: 400 bytes
Canvas cache: ~1920000 bytes
Optimization strategies:
1. Use blitting: ~5-10x speedup
2. Update only changed artists
3. Reduce figure DPI for preview
4. Cache static elements
5. Use collections for many objectsAnimation structure:
# Create figure and line artist
fig, ax = plt.subplots()
line, = ax.plot([], [])
def init():
"""Set up blank frame."""
line.set_data([], [])
return line,
def animate(frame):
"""Update for each frame."""
y = np.sin(x + frame * 0.1)
line.set_data(x, y)
return line,
# Create animation
anim = FuncAnimation(fig, animate, init_func=init,
frames=100, interval=50, blit=True)
# Save to file
anim.save('animation.mp4', writer='ffmpeg', fps=30)Blitting caches the static background and redraws only the changed artists — typically 5-10x faster than full redraws.
blit=True requires:
init()andanimate()return iterables of updated artists- Artists must be on the same axes
- Background must not change between frames
Saving animations:
- MP4:
writer='ffmpeg'(requires ffmpeg installed) - GIF:
writer='pillow' - HTML5:
anim.to_jshtml()for notebooks
Performance Optimization for Large Datasets
Visualizing large datasets requires strategic optimization to maintain interactivity.
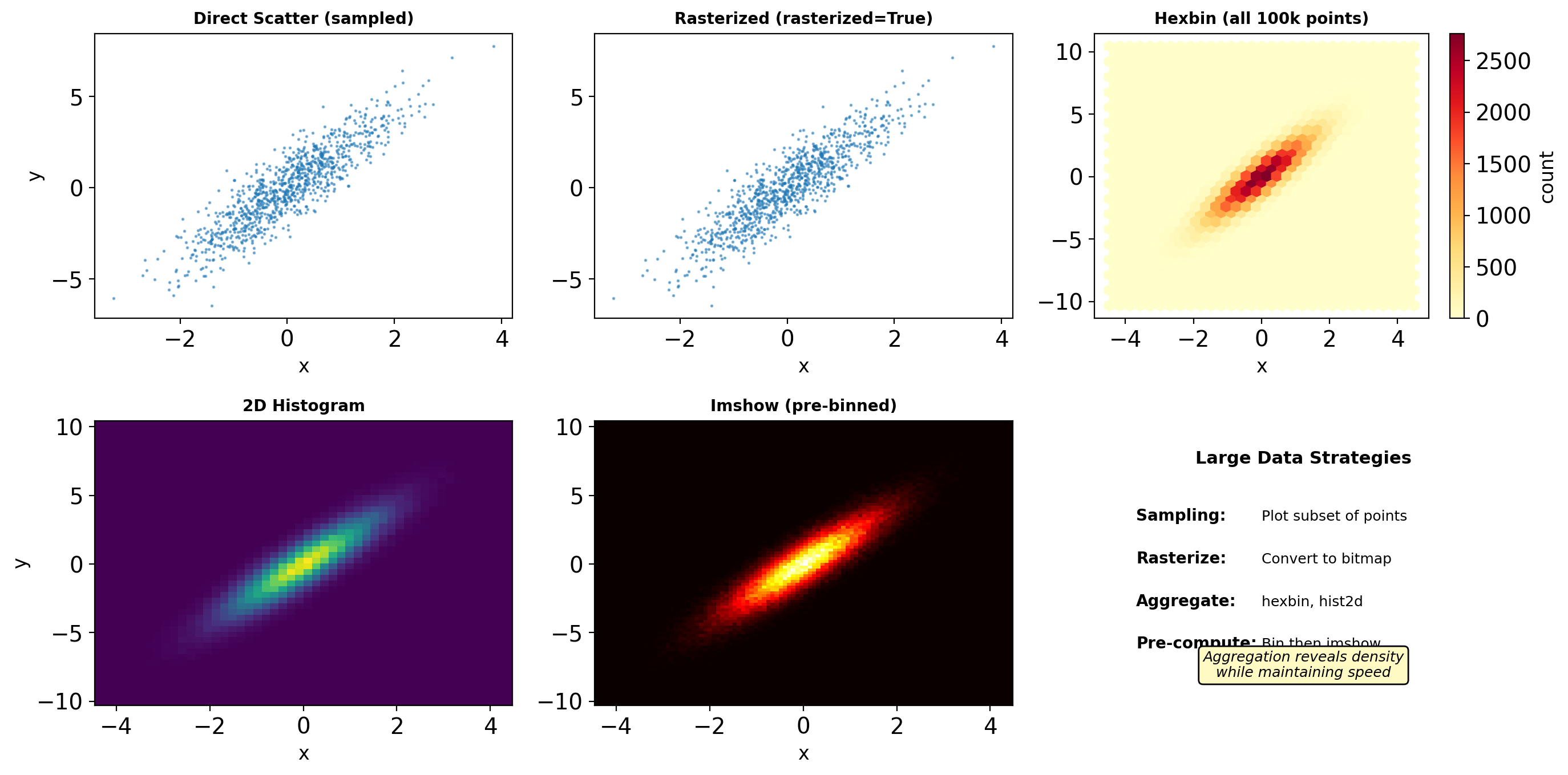
import matplotlib.pyplot as plt
import numpy as np
import time
# Generate large dataset
n_points = 50000
x = np.random.randn(n_points)
y = 2*x + np.random.randn(n_points)
# Benchmark different approaches
results = {}
# 1. Direct scatter (limited to 5k for speed)
fig, ax = plt.subplots()
start = time.perf_counter()
ax.scatter(x[:5000], y[:5000], alpha=0.5, s=1)
fig.canvas.draw()
results['scatter_5k'] = time.perf_counter() - start
plt.close()
# 2. Plot instead of scatter
fig, ax = plt.subplots()
start = time.perf_counter()
ax.plot(x, y, 'o', markersize=1, alpha=0.5)
fig.canvas.draw()
results['plot_50k'] = time.perf_counter() - start
plt.close()
# 3. Hexbin
fig, ax = plt.subplots()
start = time.perf_counter()
ax.hexbin(x, y, gridsize=30)
fig.canvas.draw()
results['hexbin_50k'] = time.perf_counter() - start
plt.close()
# 4. 2D histogram
fig, ax = plt.subplots()
start = time.perf_counter()
ax.hist2d(x, y, bins=50)
fig.canvas.draw()
results['hist2d_50k'] = time.perf_counter() - start
plt.close()
print("Rendering performance:")
for method, time_val in results.items():
print(f" {method:15s}: {time_val*1000:6.1f}ms")
# Memory usage estimation
import sys
# Scatter artist memory
fig, ax = plt.subplots()
scatter = ax.scatter(x[:1000], y[:1000])
scatter_memory = (sys.getsizeof(scatter.get_offsets()) +
sys.getsizeof(scatter.get_facecolors()))
# Line artist memory
line, = ax.plot(x[:1000], y[:1000], 'o')
line_memory = sys.getsizeof(line.get_xydata())
print(f"\nMemory usage (1000 points):")
print(f" Scatter: ~{scatter_memory/1024:.1f} KB")
print(f" Line: ~{line_memory/1024:.1f} KB")
print(f" Ratio: {scatter_memory/line_memory:.1f}x")
plt.close('all')Rendering performance:
scatter_5k : 14.4ms
plot_50k : 15.7ms
hexbin_50k : 21.2ms
hist2d_50k : 17.5ms
Memory usage (1000 points):
Scatter: ~0.3 KB
Line: ~15.8 KB
Ratio: 0.0x# Optimization strategies
class OptimizedPlotter:
"""Strategies for large dataset visualization."""
@staticmethod
def downsample(x, y, max_points=1000):
"""Randomly sample if too many points."""
n = len(x)
if n <= max_points:
return x, y
idx = np.random.choice(n, max_points, replace=False)
return x[idx], y[idx]
@staticmethod
def use_rasterization(ax, x, y):
"""Rasterize dense plots."""
ax.scatter(x, y, alpha=0.5, s=1, rasterized=True)
# Rasterized elements become bitmaps
# Faster zooming/panning
@staticmethod
def aggregate_data(x, y, bins=50):
"""Convert to density representation."""
H, xedges, yedges = np.histogram2d(x, y, bins=bins)
return H, xedges, yedges
@staticmethod
def progressive_rendering(x, y, ax):
"""Render in stages for responsiveness."""
# Quick preview
x_preview, y_preview = OptimizedPlotter.downsample(
x, y, max_points=100
)
line = ax.plot(x_preview, y_preview, 'o',
markersize=2, alpha=0.3)[0]
ax.figure.canvas.draw()
# Full render
line.set_data(x, y)
ax.figure.canvas.draw()
# Level-of-detail (LOD) system
class LODPlot:
"""Adaptive detail based on zoom level."""
def __init__(self, x, y):
self.x_full = x
self.y_full = y
self.create_levels()
def create_levels(self):
"""Create multiple resolution levels."""
self.levels = {}
n = len(self.x_full)
# Full resolution
self.levels[0] = (self.x_full, self.y_full)
# Reduced resolutions
for level in [1, 2, 3]:
step = 2 ** level
self.levels[level] = (
self.x_full[::step],
self.y_full[::step]
)
def get_data(self, zoom_level):
"""Return appropriate resolution."""
if zoom_level > 10:
return self.levels[0] # Full
elif zoom_level > 5:
return self.levels[1] # Half
elif zoom_level > 2:
return self.levels[2] # Quarter
else:
return self.levels[3] # Eighth
# Test LOD system
lod = LODPlot(x, y)
print("\nLOD system points at each level:")
for level in range(4):
x_level, y_level = lod.levels[level]
print(f" Level {level}: {len(x_level)} points")
# Chunked rendering for streaming
def chunked_plot(x, y, ax, chunk_size=5000):
"""Plot data in chunks to maintain responsiveness."""
n_chunks = len(x) // chunk_size + 1
for i in range(n_chunks):
start = i * chunk_size
end = min((i + 1) * chunk_size, len(x))
ax.plot(x[start:end], y[start:end], 'o',
markersize=1, alpha=0.5)
# Allow GUI to update
if i % 5 == 0:
ax.figure.canvas.draw()
plt.pause(0.001)
print("\nOptimization impact:")
print(" Rasterization: 2-5x faster interaction")
print(" Aggregation: 10-100x data reduction")
print(" LOD: Adaptive performance")
LOD system points at each level:
Level 0: 50000 points
Level 1: 25000 points
Level 2: 12500 points
Level 3: 6250 points
Optimization impact:
Rasterization: 2-5x faster interaction
Aggregation: 10-100x data reduction
LOD: Adaptive performanceBackend Selection and Output Formats
Different backends optimize for different use cases: interactivity vs. publication quality.
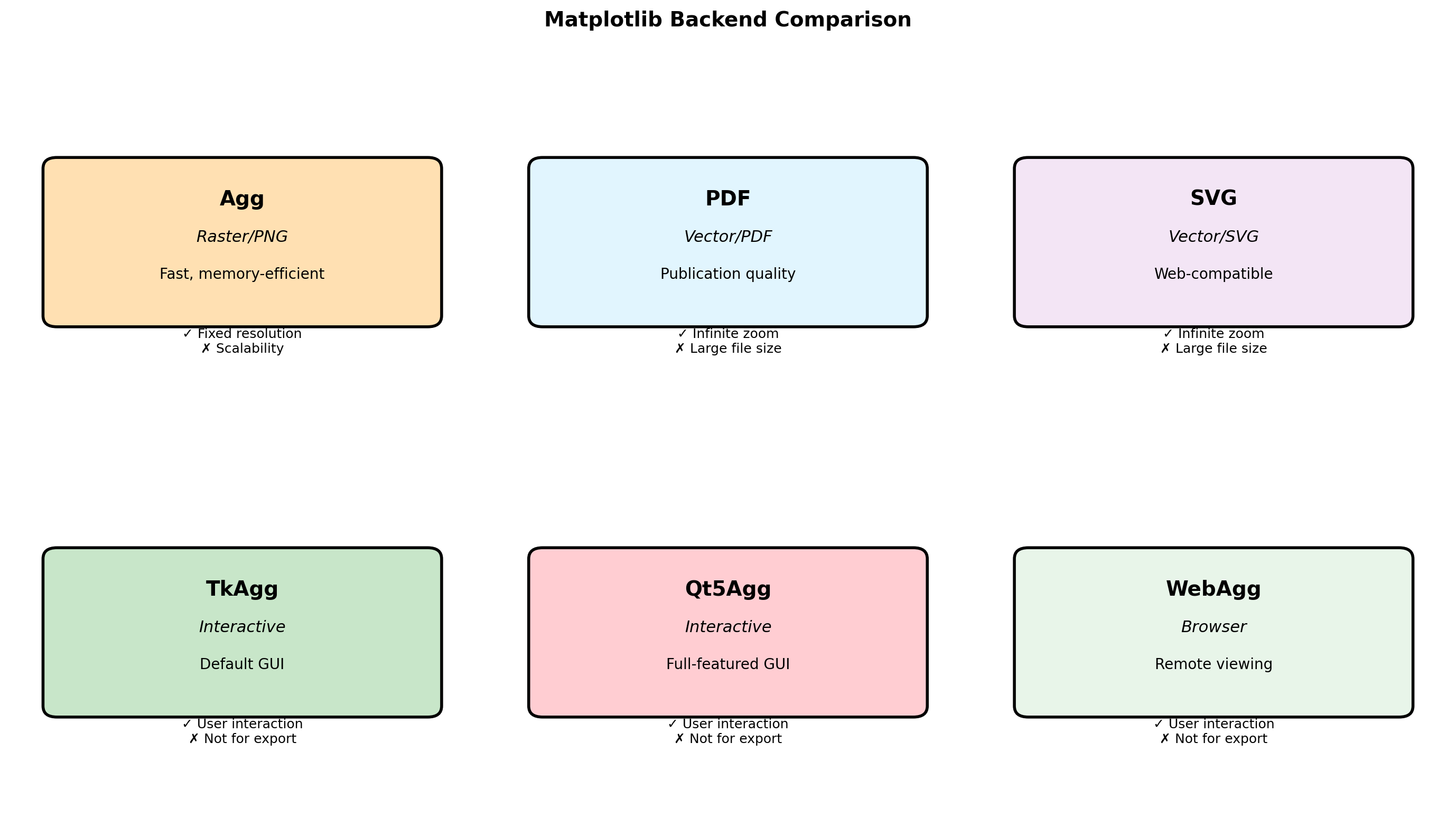
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import os
# Check available backends
print("Available backends:")
for backend in matplotlib.rcsetup.all_backends:
print(f" {backend}")
print(f"\nCurrent backend: {matplotlib.get_backend()}")
# Create test figure
fig, ax = plt.subplots(figsize=(6, 4))
x = np.linspace(0, 10, 1000)
ax.plot(x, np.sin(x), 'b-', linewidth=2)
ax.fill_between(x, 0, np.sin(x), alpha=0.3)
ax.set_title('Test Figure')
ax.grid(True, alpha=0.3)
# Save in different formats
formats = {
'png': {'dpi': 100, 'bbox_inches': 'tight'},
'pdf': {'bbox_inches': 'tight'},
'svg': {'bbox_inches': 'tight'},
'eps': {'bbox_inches': 'tight'},
}
file_sizes = {}
import time
for fmt, kwargs in formats.items():
filename = f'test_figure.{fmt}'
start = time.perf_counter()
fig.savefig(filename, format=fmt, **kwargs)
save_time = time.perf_counter() - start
# Check file size
if os.path.exists(filename):
size = os.path.getsize(filename) / 1024 # KB
file_sizes[fmt] = (size, save_time)
os.remove(filename) # Clean up
print("\nOutput format comparison:")
print(f"{'Format':<10} {'Size (KB)':<12} {'Time (ms)':<10}")
print("-" * 35)
for fmt, (size, save_time) in file_sizes.items():
print(f"{fmt:<10} {size:<12.1f} {save_time*1000:<10.1f}")
plt.close()
# DPI impact on file size
dpis = [72, 100, 150, 200, 300]
sizes = []
times = []
for dpi in dpis:
start = time.perf_counter()
fig.savefig('temp.png', dpi=dpi)
times.append(time.perf_counter() - start)
sizes.append(os.path.getsize('temp.png') / 1024)
os.remove('temp.png')
print("\nDPI impact (PNG):")
print(f"{'DPI':<10} {'Size (KB)':<12} {'Time (ms)':<10}")
print("-" * 35)
for dpi, size, save_time in zip(dpis, sizes, times):
print(f"{dpi:<10} {size:<12.1f} {save_time*1000:<10.1f}")Available backends:
gtk3agg
gtk3cairo
gtk4agg
gtk4cairo
macosx
nbagg
notebook
qtagg
qtcairo
qt5agg
qt5cairo
tkagg
tkcairo
webagg
wx
wxagg
wxcairo
agg
cairo
pdf
pgf
ps
svg
template
Current backend: module://matplotlib_inline.backend_inline
Output format comparison:
Format Size (KB) Time (ms)
-----------------------------------
png 23.4 29.1
pdf 23.2 467.8
svg 68.8 21.5
eps 62.9 21.8
DPI impact (PNG):
DPI Size (KB) Time (ms)
-----------------------------------
72 15.7 12.2
100 23.8 14.9
150 36.7 22.7
200 51.4 33.3
300 82.3 63.2 # Backend-specific optimizations
import matplotlib.pyplot as plt
import numpy as np
# Configure for publication
def setup_publication():
"""Configure matplotlib for publication."""
plt.rcParams.update({
'font.size': 10,
'font.family': 'serif',
'text.usetex': False, # Set True for LaTeX
'axes.linewidth': 1.5,
'axes.labelsize': 11,
'axes.titlesize': 12,
'xtick.labelsize': 10,
'ytick.labelsize': 10,
'legend.fontsize': 10,
'figure.dpi': 100,
'savefig.dpi': 300,
'savefig.bbox': 'tight',
'savefig.pad_inches': 0.1,
})
# Configure for presentation
def setup_presentation():
"""Configure matplotlib for slides."""
plt.rcParams.update({
'font.size': 14,
'font.family': 'sans-serif',
'axes.linewidth': 2,
'axes.labelsize': 16,
'axes.titlesize': 18,
'lines.linewidth': 3,
'lines.markersize': 10,
'xtick.labelsize': 14,
'ytick.labelsize': 14,
'legend.fontsize': 14,
'figure.dpi': 100,
'savefig.dpi': 150,
})
# Backend-specific features
def interactive_features():
"""Features only available in interactive backends."""
fig, ax = plt.subplots()
ax.plot([1, 2, 3], [1, 4, 2])
# Only works with interactive backends
if matplotlib.get_backend().endswith('Agg'):
print("Non-interactive backend - no GUI features")
else:
# These would work in interactive mode
print("Interactive features available:")
print(" - fig.canvas.mpl_connect('button_press_event', callback)")
print(" - plt.ginput(n=3) # Get n mouse clicks")
print(" - plt.waitforbuttonpress()")
plt.close()
interactive_features()
# Format selection guide
print("\nFormat selection guide:")
print(" PNG: Web, general use, fixed resolution")
print(" PDF: LaTeX, publications, vector graphics")
print(" SVG: Web animations, editing, vector")
print(" EPS: Legacy publications, PostScript")
# Memory vs quality tradeoff
print("\nMemory/Quality tradeoffs:")
print(" Rasterized=True: Reduces PDF size for dense plots")
print(" DPI: Higher = better quality, larger files")
print(" Compression: PNG supports lossless compression")Interactive features available:
- fig.canvas.mpl_connect('button_press_event', callback)
- plt.ginput(n=3) # Get n mouse clicks
- plt.waitforbuttonpress()
Format selection guide:
PNG: Web, general use, fixed resolution
PDF: LaTeX, publications, vector graphics
SVG: Web animations, editing, vector
EPS: Legacy publications, PostScript
Memory/Quality tradeoffs:
Rasterized=True: Reduces PDF size for dense plots
DPI: Higher = better quality, larger files
Compression: PNG supports lossless compression