Classification and Logistic Regression
EE 541 - Unit 5
Fall 2025
Outline
1. Decision Theory
- Probabilistic vs deterministic approaches
- Loss functions and Bayes risk
- MAP rule from uniform loss
- Medical diagnosis
- Reject option
- Calibration vs discrimination
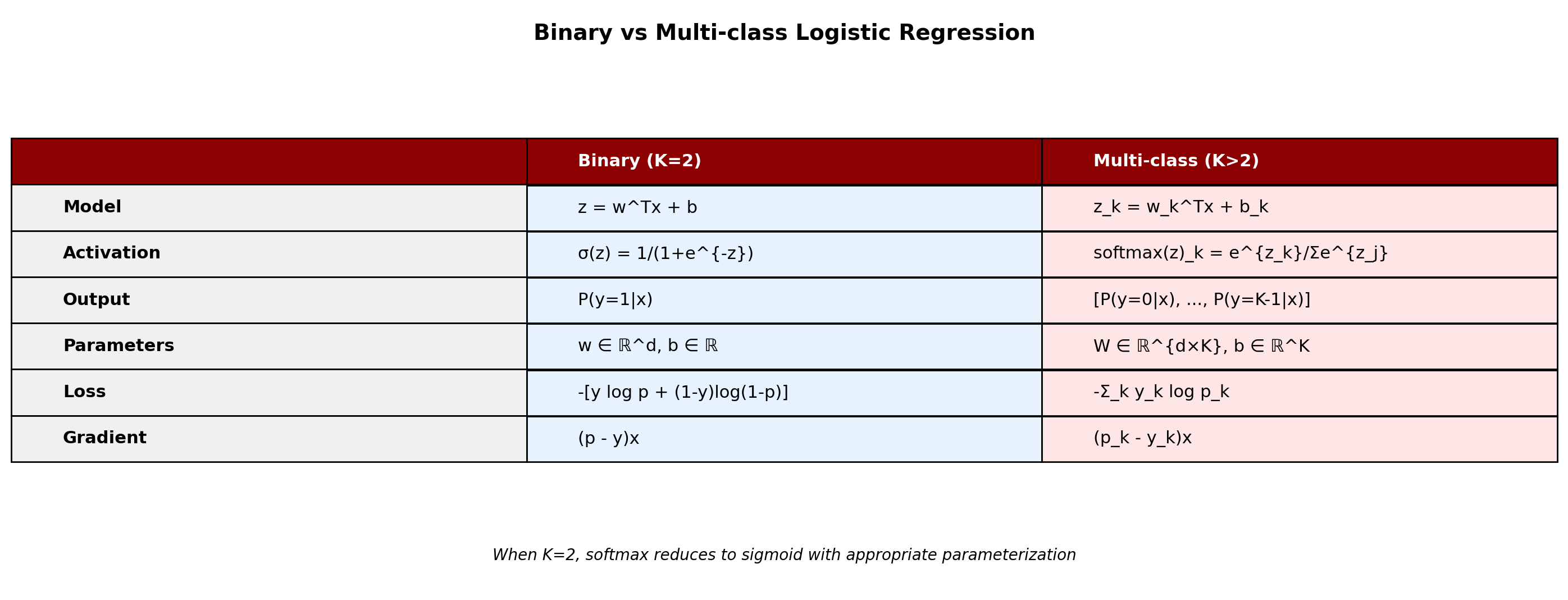
2. Logistic Regression
- Linear models fail for probabilities
- Log-odds transformation
- Sigmoid function properties
- Bernoulli likelihood
- Gradient: \((y - p)\mathbf{x}\)
3. Extensions
- Multi-Class: Softmax
- Regularization: L2/L1 penalties
- Neural Networks: XOR problem
Decision Theory
Binary Classification Problem
Task: Given features \(\mathbf{x} \in \mathbb{R}^d\), predict class \(y \in \{0, 1\}\)
Classical approach: Find decision boundary \[\hat{y} = \begin{cases} 1 & \text{if } f(\mathbf{x}) > 0 \\ 0 & \text{otherwise} \end{cases}\]
Probabilistic approach: Estimate \(P(y=1|\mathbf{x})\) \[\hat{p} = P(y=1|\mathbf{x}) \in [0, 1]\] \[\hat{y} = \mathbb{1}[\hat{p} > \tau]\]
Main challenges:
- How do we model \(P(y|\mathbf{x})\)?
- What loss function captures objective?
- What threshold \(\tau\) minimizes expected cost?
From Probabilities to Decisions
The classification pipeline:
- Model: Estimate \(P(y=1|\mathbf{x})\)
- Training: Learn parameters from data
- Inference: Compute \(p = P(y=1|\mathbf{x}_{\text{new}})\)
- Decision: Choose \(\hat{y} \in \{0, 1\}\)
After obtaining probabilities, how do we decide?
Simple threshold: \[\hat{y} = \begin{cases} 1 & p > 0.5 \\ 0 & p \leq 0.5 \end{cases}\]
But this assumes all errors cost the same
Example: Credit card fraud
- False positive: Block legitimate transaction ($10 cost)
- False negative: Approve fraud ($1000 loss)
Optimal threshold depends on these costs
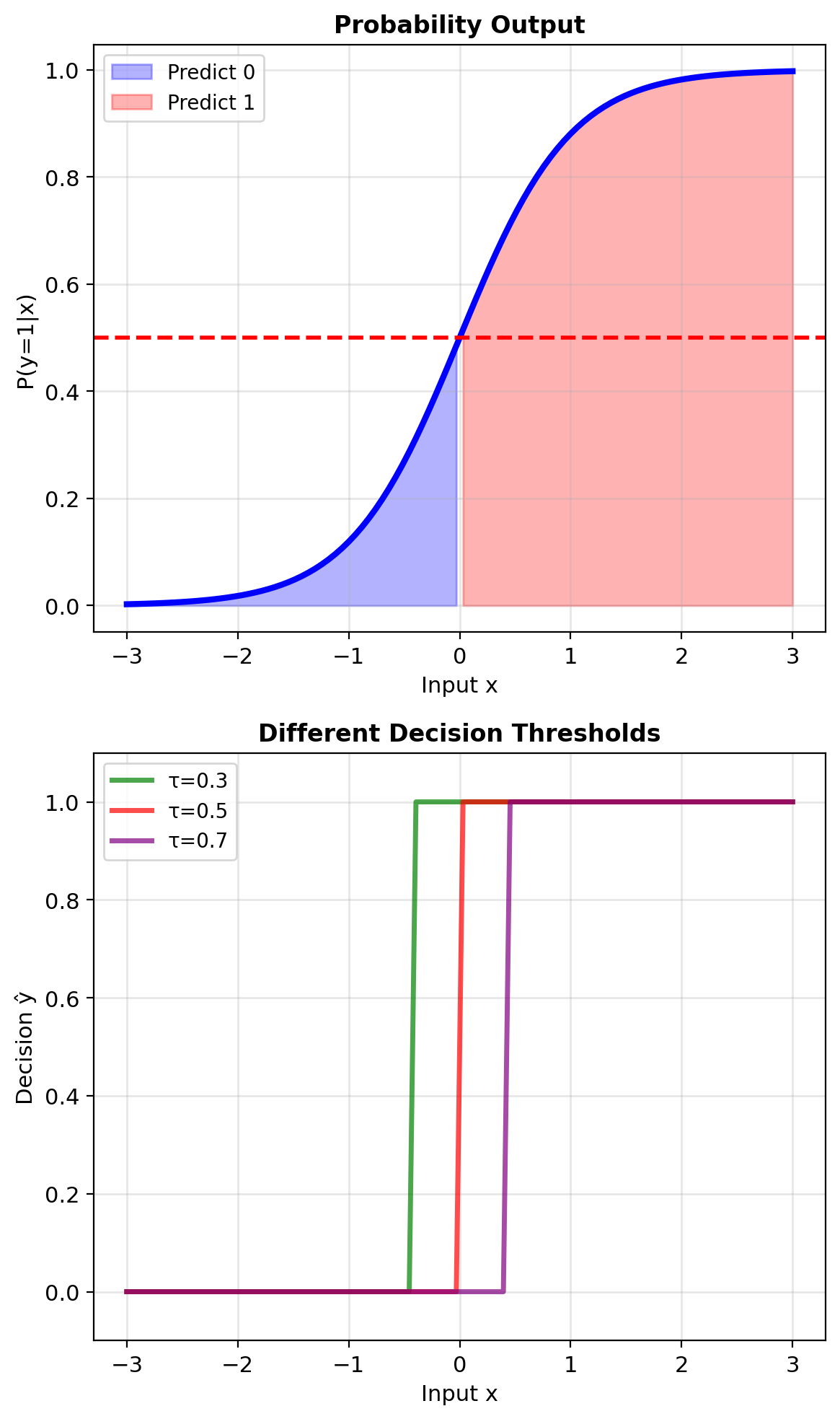
Different thresholds lead to different decisions
Decision Theory – Components of a decision problem
States (observations): \(\Omega = \{\omega_1, \omega_2, \ldots\}\)
- True class labels: \(y \in \{0, 1\}\) or \(\{1, 2, \ldots, K\}\)
Actions: \(\mathcal{A} = \{a_1, a_2, \ldots\}\)
- Predicted labels: \(\hat{y}\)
- Or “reject” option (defer to human)
Decision rule: \(\delta: \mathcal{X} \to \mathcal{A}\)
- Maps observations to actions
Loss function: \(L: \Omega \times \mathcal{A} \to \mathbb{R}\)
- Cost of action \(a\) when true state is \(\omega\)
Objective: Minimize expected loss \[R(\delta) = \mathbb{E}[L(Y, \delta(X))]\]
Bayes risk: Minimum achievable expected loss \[R^* = \inf_\delta R(\delta)\]
Bayesian Decision Theory Foundation
Bayes risk minimization:
Given observation \(\mathbf{x}\), choose action to minimize expected loss:
\[\delta^*(\mathbf{x}) = \arg\min_{a \in \mathcal{A}} \mathbb{E}[L(Y, a) | \mathbf{X} = \mathbf{x}]\]
Expanding the expectation: \[= \arg\min_{a} \sum_{k} L(k, a) \cdot P(Y=k|\mathbf{x})\]
For binary classification with \(y \in \{0, 1\}\): \[\delta^*(\mathbf{x}) = \arg\min_{a \in \{0,1\}} \left[ L(0,a)(1-p) + L(1,a)p \right]\]
where \(p = P(Y=1|\mathbf{x})\)
Optimal decisions depend on:
- Posterior probabilities \(P(Y=k|\mathbf{x})\)
- Loss function \(L(k, a)\)
Bayes rule minimizes expected loss at each point
Uniform Loss Leads to MAP Rule
0-1 Loss (uniform error cost): \[L(y, \hat{y}) = \begin{cases} 0 & \text{if } y = \hat{y} \\ 1 & \text{if } y \neq \hat{y} \end{cases}\]
Expected loss for action \(a\): \[\mathbb{E}[L(Y, a) | \mathbf{x}] = \sum_{k \neq a} P(Y=k|\mathbf{x}) = 1 - P(Y=a|\mathbf{x})\]
Minimizing expected loss: \[\delta^*(\mathbf{x}) = \arg\min_a [1 - P(Y=a|\mathbf{x})] = \arg\max_a P(Y=a|\mathbf{x})\]
This is the MAP rule!
\[\boxed{\delta_{\text{MAP}}(\mathbf{x}) = \arg\max_k P(Y=k|\mathbf{x})}\]
MAP minimizes error probability when all errors cost the same
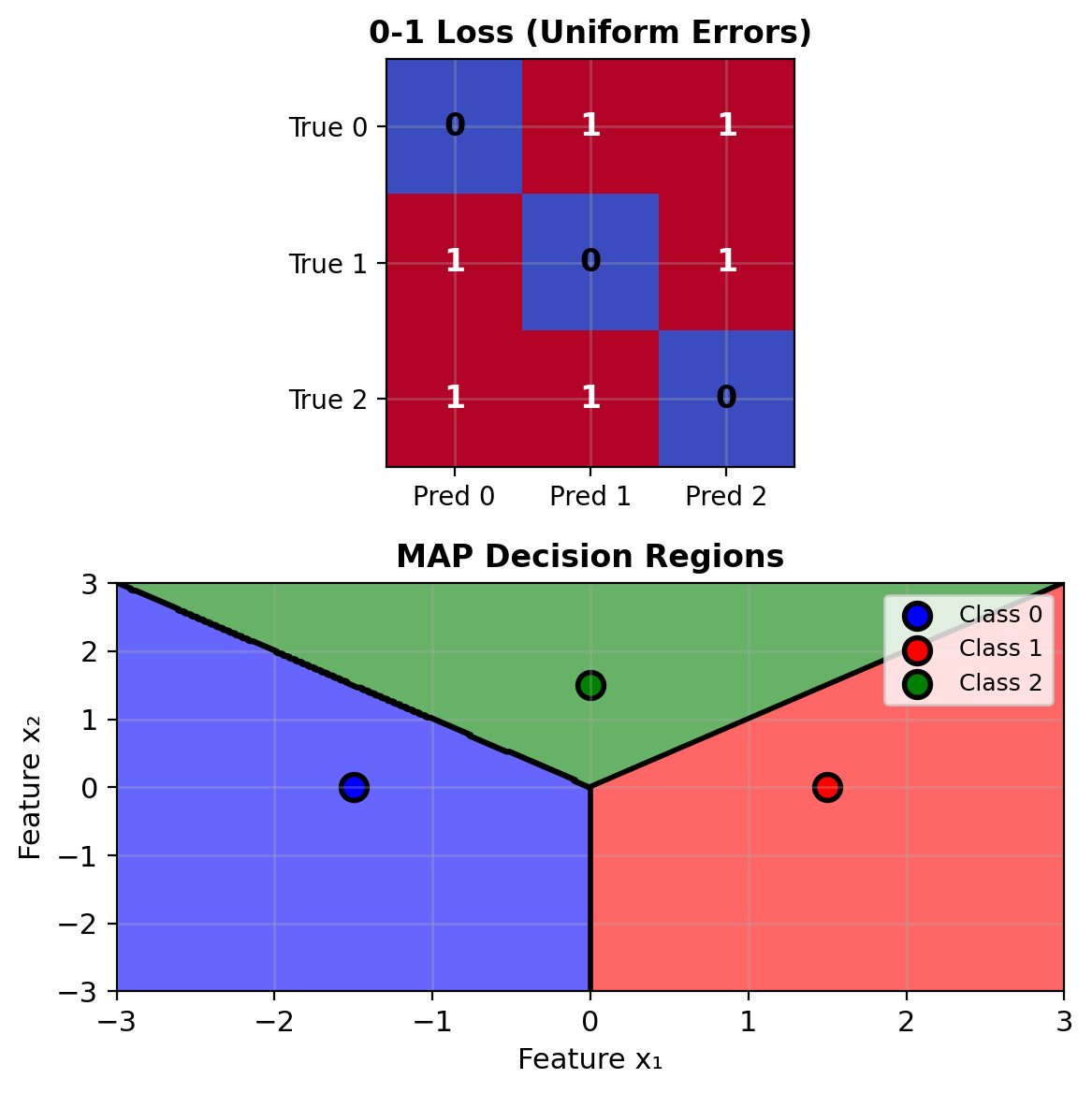
Each region: highest posterior probability wins
Likelihood Ratio Test for Binary Classification
Binary Bayes decision rule:
Choose class 1 if “expected loss of choosing 1” < “expected loss of choosing 0”:
\[L_{01}P(Y=0|\mathbf{x}) < L_{10}P(Y=1|\mathbf{x})\]
where \(L_{ij}\) = loss of predicting \(j\) when true class is \(i\)
Using Bayes theorem: \[P(Y=k|\mathbf{x}) = \frac{p(\mathbf{x}|Y=k)P(Y=k)}{p(\mathbf{x})}\]
Rearranging: \[\frac{p(\mathbf{x}|Y=1)}{p(\mathbf{x}|Y=0)} > \frac{L_{01}P(Y=0)}{L_{10}P(Y=1)}\]
Likelihood Ratio Test: \[\boxed{\Lambda(\mathbf{x}) = \frac{p(\mathbf{x}|Y=1)}{p(\mathbf{x}|Y=0)} \underset{H_0}{\overset{H_1}{\gtrless}} \tau}\]
where threshold \(\tau = \frac{L_{01}P(Y=0)}{L_{10}P(Y=1)}\)
Log-likelihood ratio (more stable): \[\log \Lambda(\mathbf{x}) = \log p(\mathbf{x}|Y=1) - \log p(\mathbf{x}|Y=0)\]

Linear boundary in log-space → stability
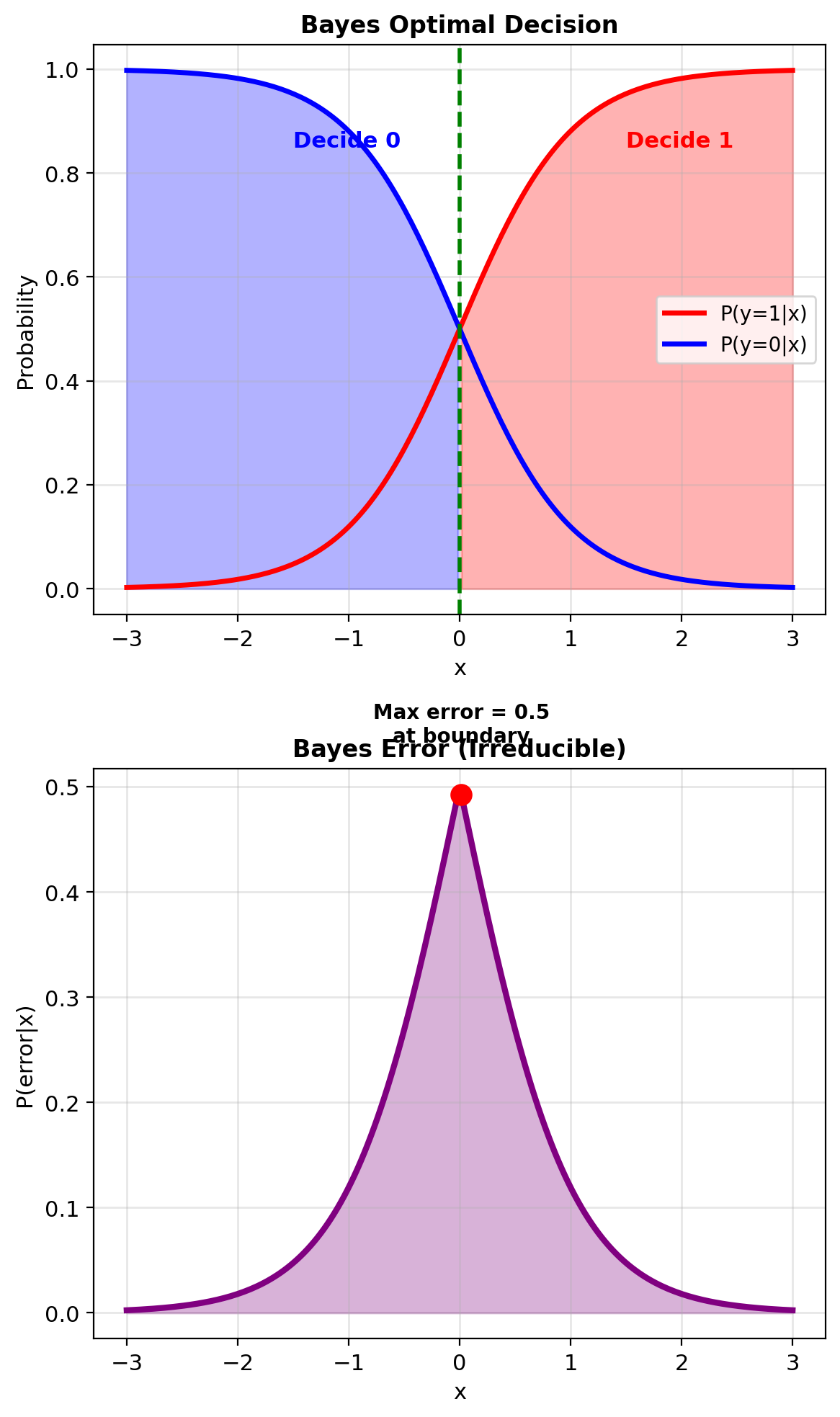
Bayes Optimal Classifier
For 0-1 loss (all errors equal): \[L(y, \hat{y}) = \mathbb{1}[y \neq \hat{y}] = \begin{cases} 0 & y = \hat{y} \\ 1 & y \neq \hat{y} \end{cases}\]
Expected loss for predicting class \(k\): \[\mathbb{E}[L(Y, k)|X=\mathbf{x}] = \sum_{j \neq k} P(Y=j|\mathbf{x})\] \[= 1 - P(Y=k|\mathbf{x})\]
Bayes optimal decision: \[\hat{y}^* = \arg\max_k P(Y=k|\mathbf{x})\]
Choose the most probable class.
Bayes error rate: \[\epsilon^* = \mathbb{E}[1 - \max_k P(Y=k|X)]\]
This is the irreducible error
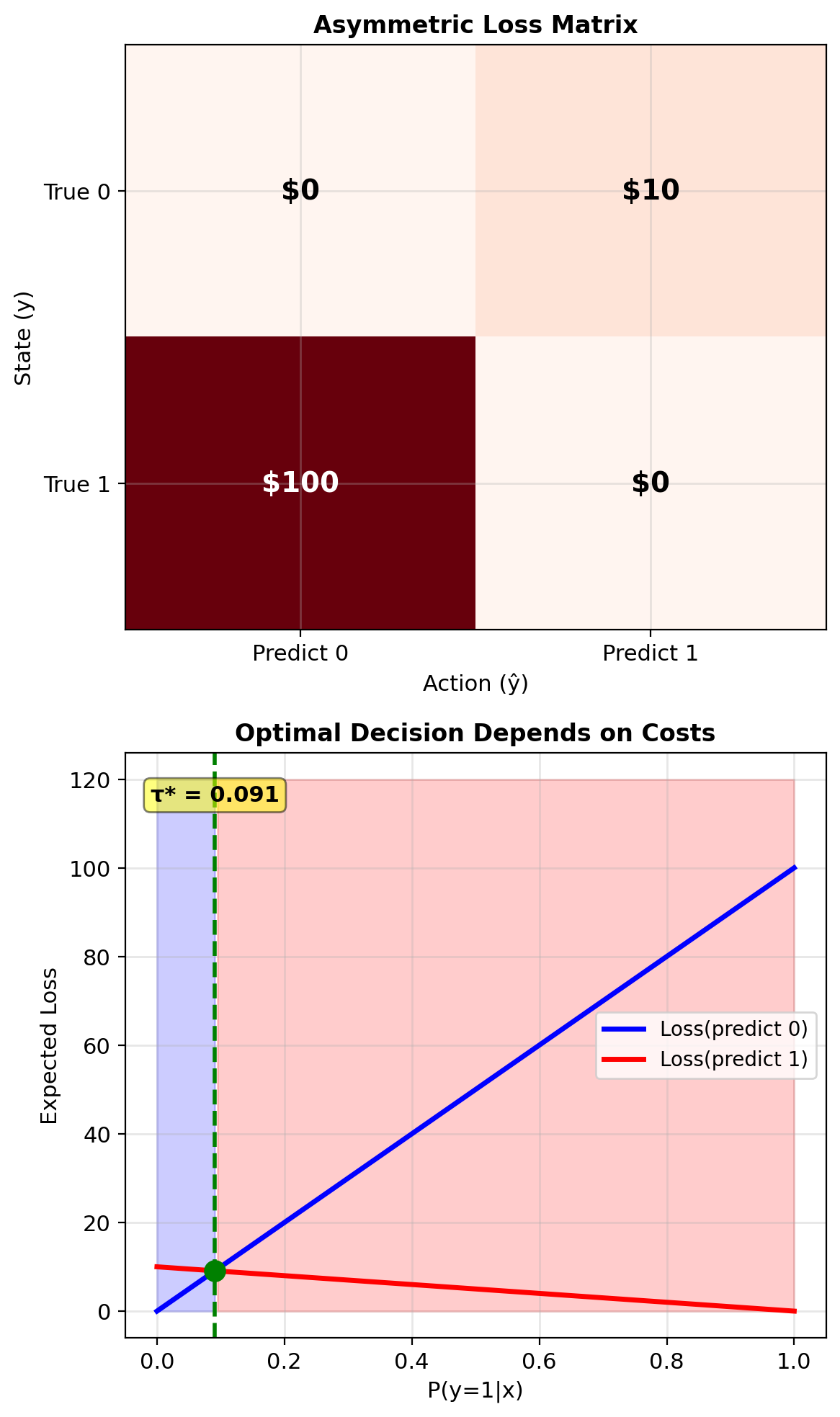
General Loss Functions
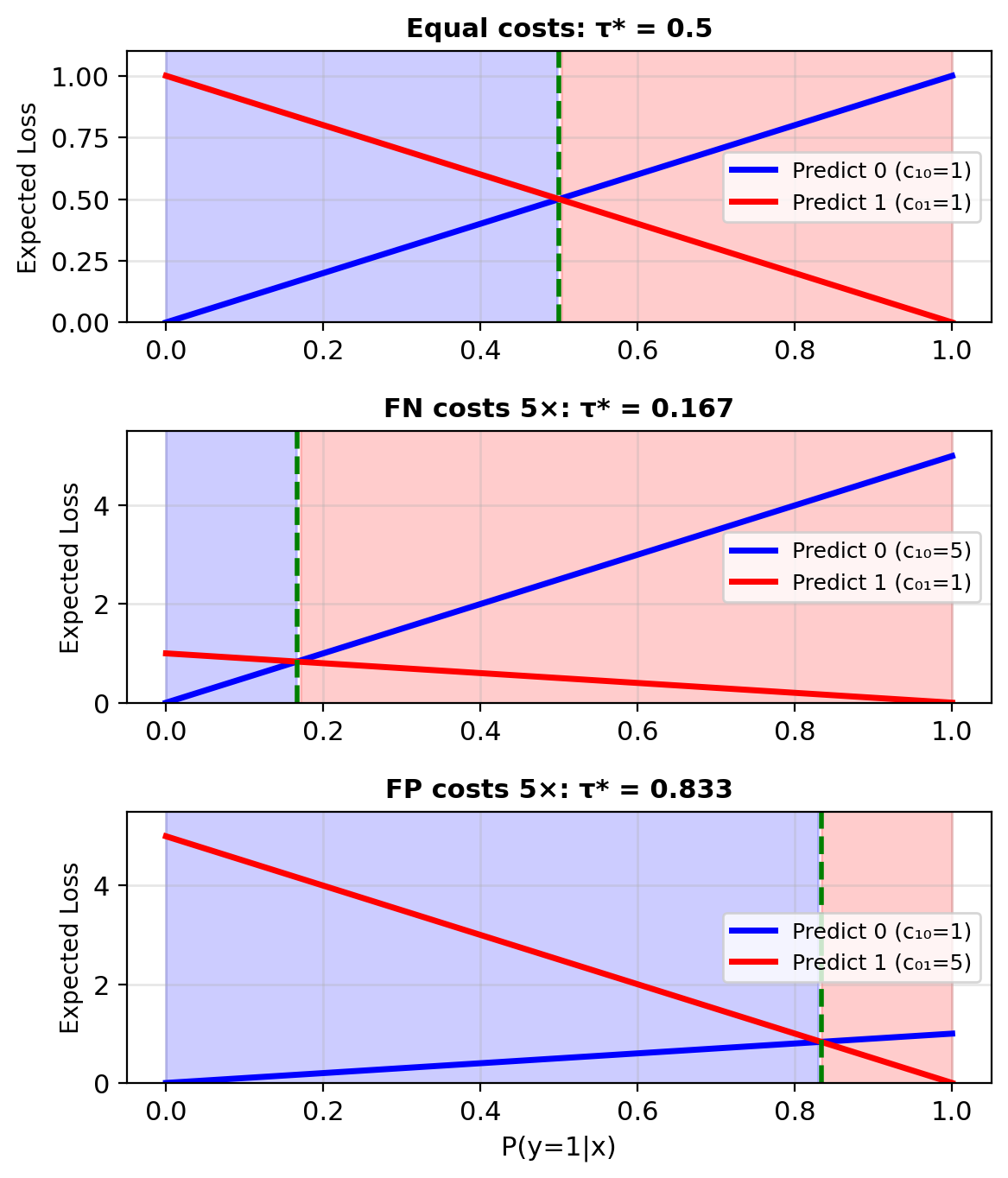
Binary classification with costs:
\[L = \begin{bmatrix} 0 & c_{01} \\ c_{10} & 0 \end{bmatrix}\]
where:
- \(c_{01}\): Cost of false positive (say 1 when true is 0)
- \(c_{10}\): Cost of false negative (say 0 when true is 1)
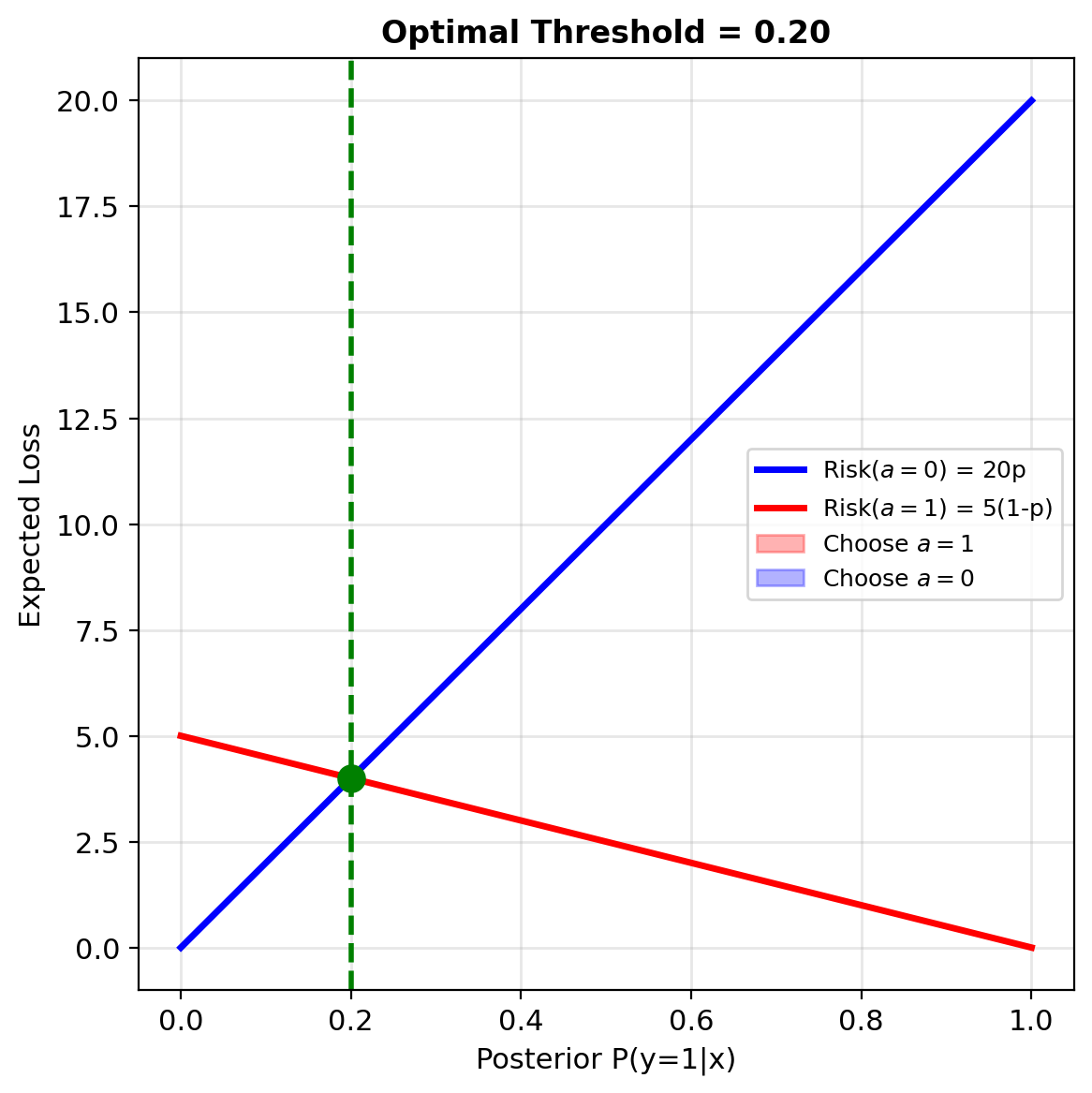
Expected loss of predicting 1: \[R_1(\mathbf{x}) = c_{01} \cdot P(y=0|\mathbf{x})\]
Expected loss of predicting 0: \[R_0(\mathbf{x}) = c_{10} \cdot P(y=1|\mathbf{x})\]
Optimal decision: Predict 1 if \(R_1(\mathbf{x}) < R_0(\mathbf{x})\)
\[c_{01}(1-p) < c_{10} \cdot p\] \[p > \frac{c_{01}}{c_{01} + c_{10}}\]
Optimal threshold: \(\tau^* = \frac{c_{01}}{c_{01} + c_{10}}\)
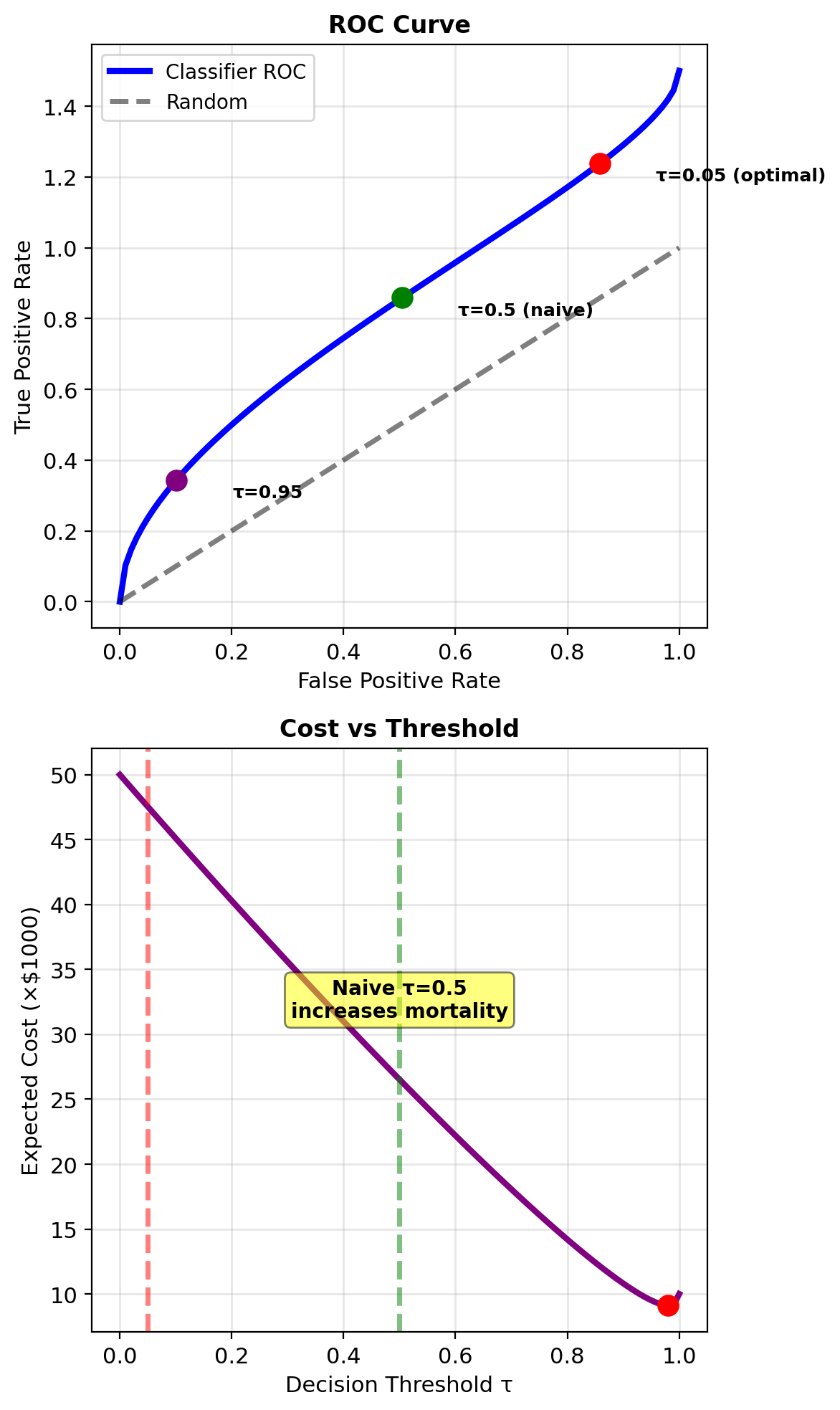
Medical Diagnosis Example
Cancer screening scenario:
- State: Cancer (1) or Healthy (0)
- Action: Treat (1) or Don’t treat (0)
Realistic costs:
- False negative (miss cancer): Death = $1,000,000
- False positive (unnecessary treatment): $50,000
- True positive (treat cancer): $50,000
- True negative (no treatment): $0
Loss matrix: \[L = \begin{bmatrix} 0 & 50,000 \\ 1,000,000 & 50,000 \end{bmatrix}\]
Note: treatment cost even for true positives
Optimal threshold: \[\tau^* = \frac{50,000}{50,000 + 950,000} = 0.05\]
Treat if \(P(\text{cancer}|\text{test}) > 0.05\)
The Reject Option
Three-way decision:
- Predict class 0
- Predict class 1
- Reject (defer to expert)
Extended loss matrix: \[L = \begin{bmatrix} 0 & c_{01} & c_r \\ c_{10} & 0 & c_r \end{bmatrix}\]
where \(c_r\) = cost of rejection (expert review)
Decision regions:
- Predict 0 if \(p < \tau_1\)
- Reject if \(\tau_1 \leq p \leq \tau_2\)
- Predict 1 if \(p > \tau_2\)
Optimal thresholds (for symmetric costs): \[\tau_1 = \frac{c_r}{c_{10}}, \quad \tau_2 = 1 - \frac{c_r}{c_{01}}\]
Reject when model confidence is low
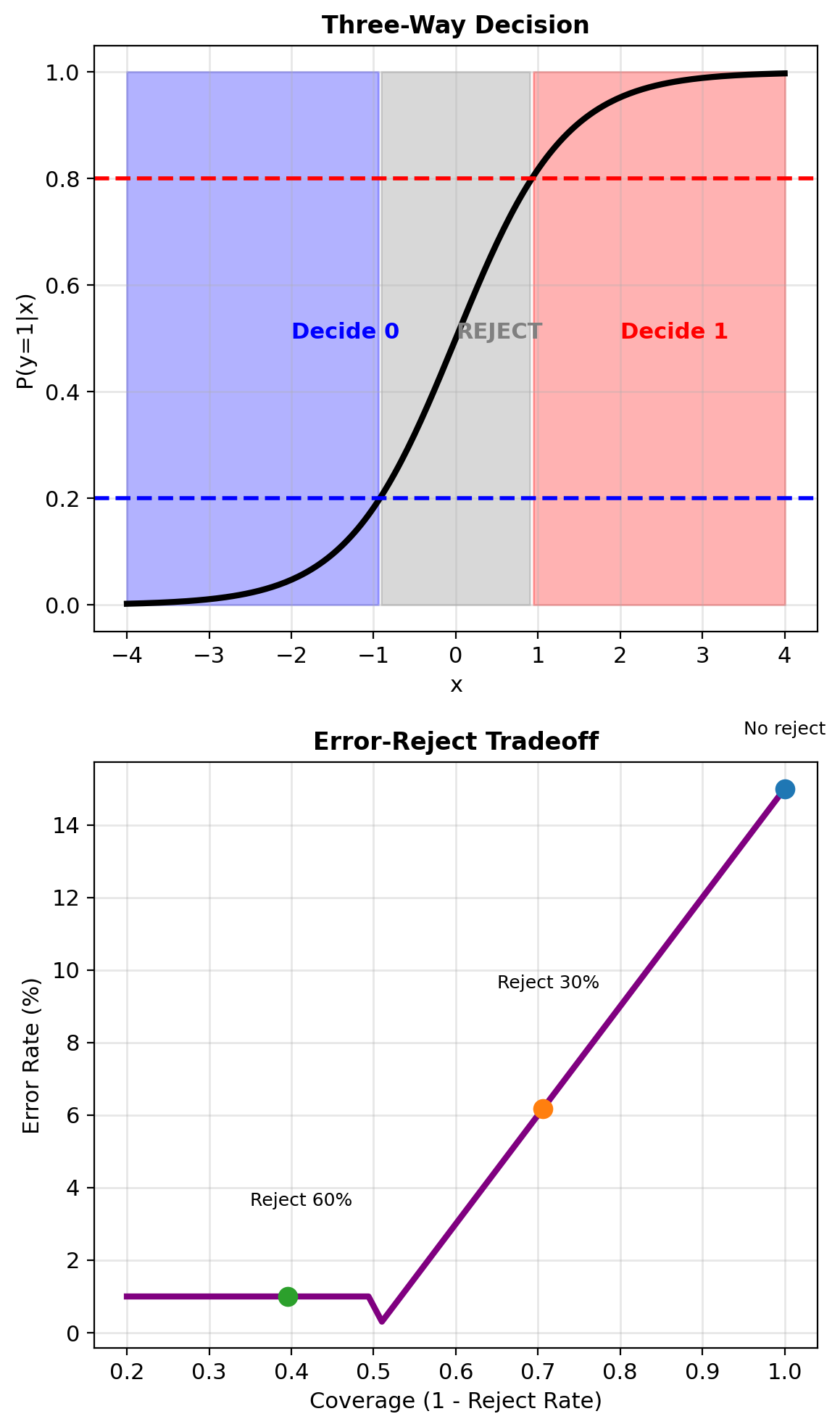
Reject option reduces error on uncertain samples
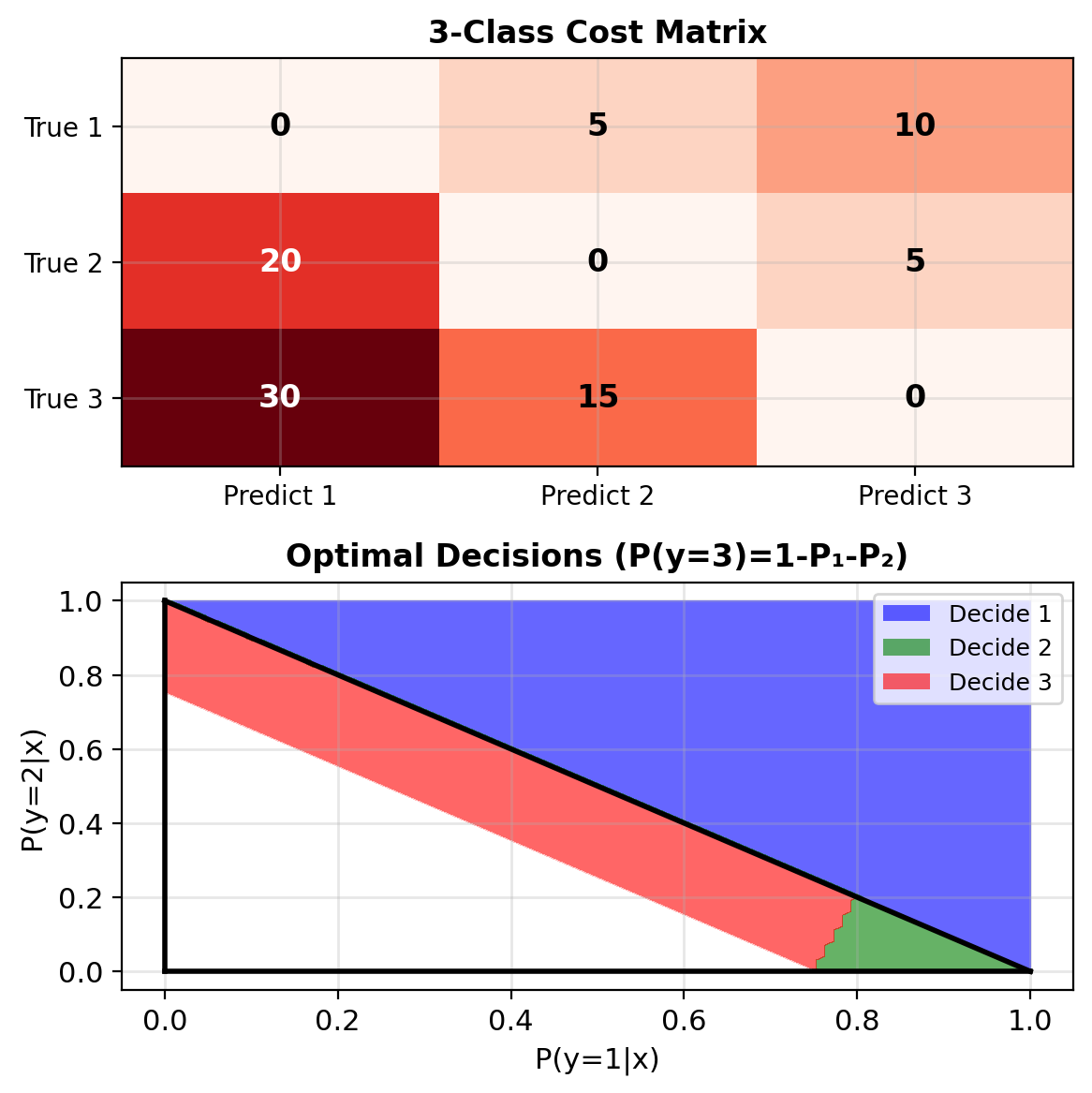
Multi-Class Decisions
K-class cost matrix: \(L \in \mathbb{R}^{K \times K}\)
\[L_{ij} = \text{cost of predicting } j \text{ when true is } i\]
Expected loss for action \(a\): \[R_a(\mathbf{x}) = \sum_{k=1}^K L_{ka} \cdot P(y=k|\mathbf{x})\]
Optimal decision: \[\hat{y}^* = \arg\min_a R_a(\mathbf{x})\]
Example: 3-class with varying costs \[L = \begin{bmatrix} 0 & 5 & 10 \\ 20 & 0 & 5 \\ 30 & 15 & 0 \end{bmatrix}\]
Must compute expected loss for each action
Special case: If \(L_{ij} = 1 - \delta_{ij}\) (0-1 loss), reduces to argmax of posteriors
Hard vs Soft Decisions
Hard decisions: \(\hat{y} \in \{0, 1, ..., K-1\}\)
- Single class prediction
- Required for final action
- Information loss through discretization
Soft decisions: \(\mathbf{p} = [p_0, p_1, ..., p_{K-1}]\)
- Full distribution of outcomes
- Preserves uncertainty information
- Useful for downstream processing
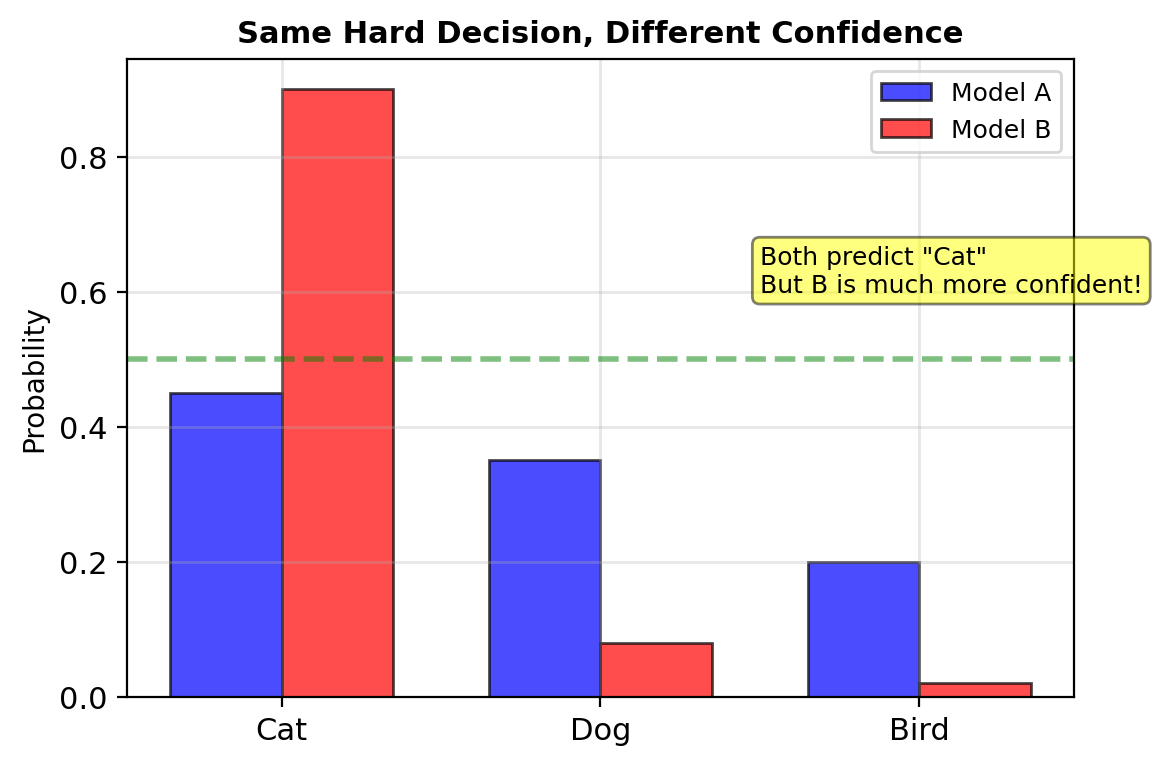
Soft decisions ideal for:
- Cascaded systems: Next stage uses probabilities
- Speech recognition → language model
- Object detection → tracking
- Confidence assessment: Reliability measures
- Medical diagnosis (refer if uncertain)
- Autonomous driving (hand off to human)
- Cost-sensitive decisions: Context-dependent losses
- Fraud detection (amount matters)
- Email filtering (sender importance)
- Ensemble methods: Combining multiple models
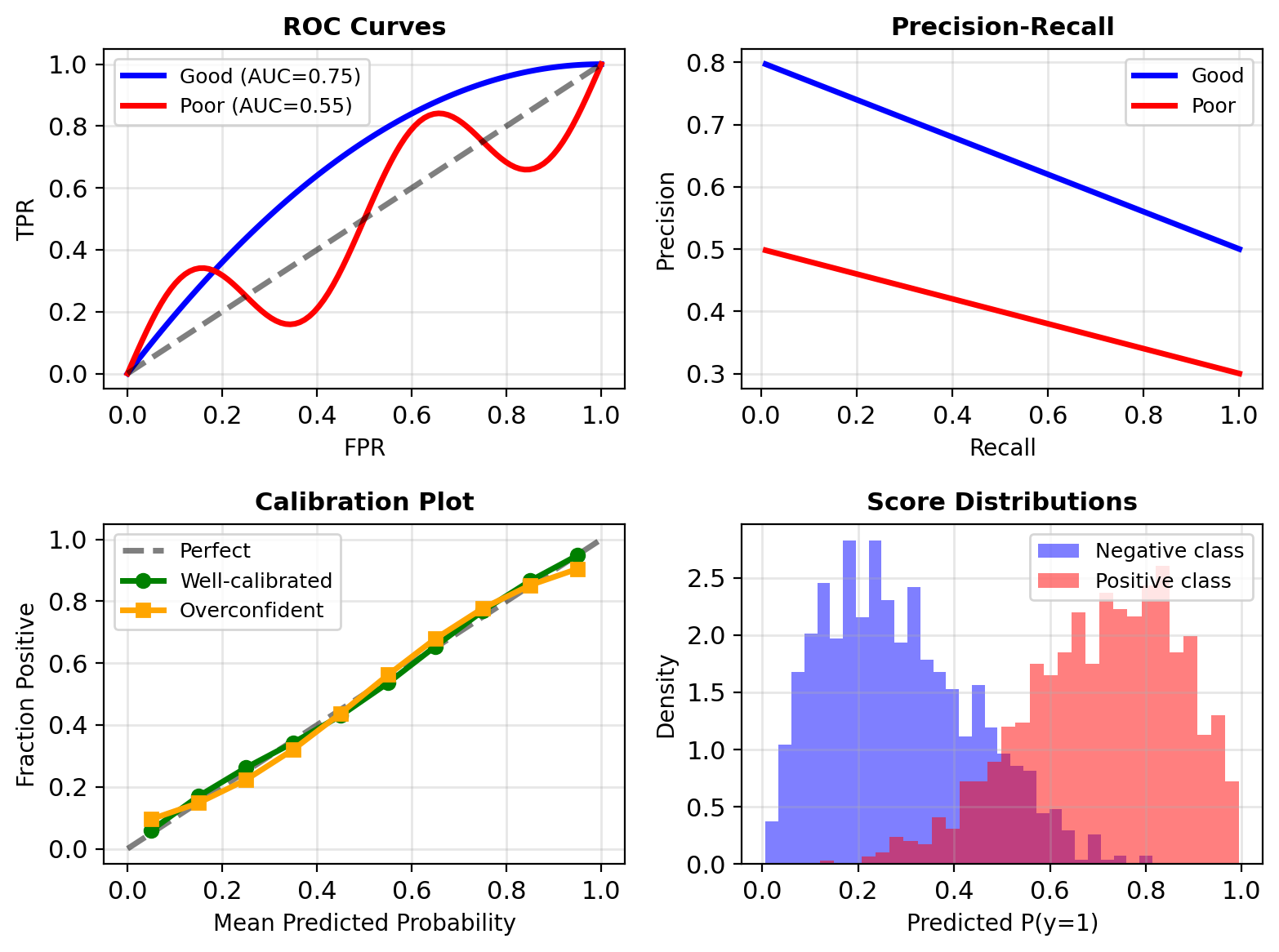
Beyond Accuracy – Evaluating Probabilistic Classifiers
1. Discrimination (ranking ability):
- ROC curve: TPR vs FPR
- AUC: Area under ROC
- Precision-Recall curve
2. Calibration (probability accuracy):
- Do predicted probabilities match frequencies?
- Among all \(\mathbf{x}\) where \(P(y=1|\mathbf{x}) = 0.7\), is the true fraction positive ≈ 70%?
3. Proper scoring rules:
- Log-loss: \(-\sum_i [y_i \log p_i + (1-y_i)\log(1-p_i)]\)
- Brier score: \(\sum_i (y_i - p_i)^2\)
These penalize both discrimination and calibration errors
Note: Good discrimination ≠ Good calibration
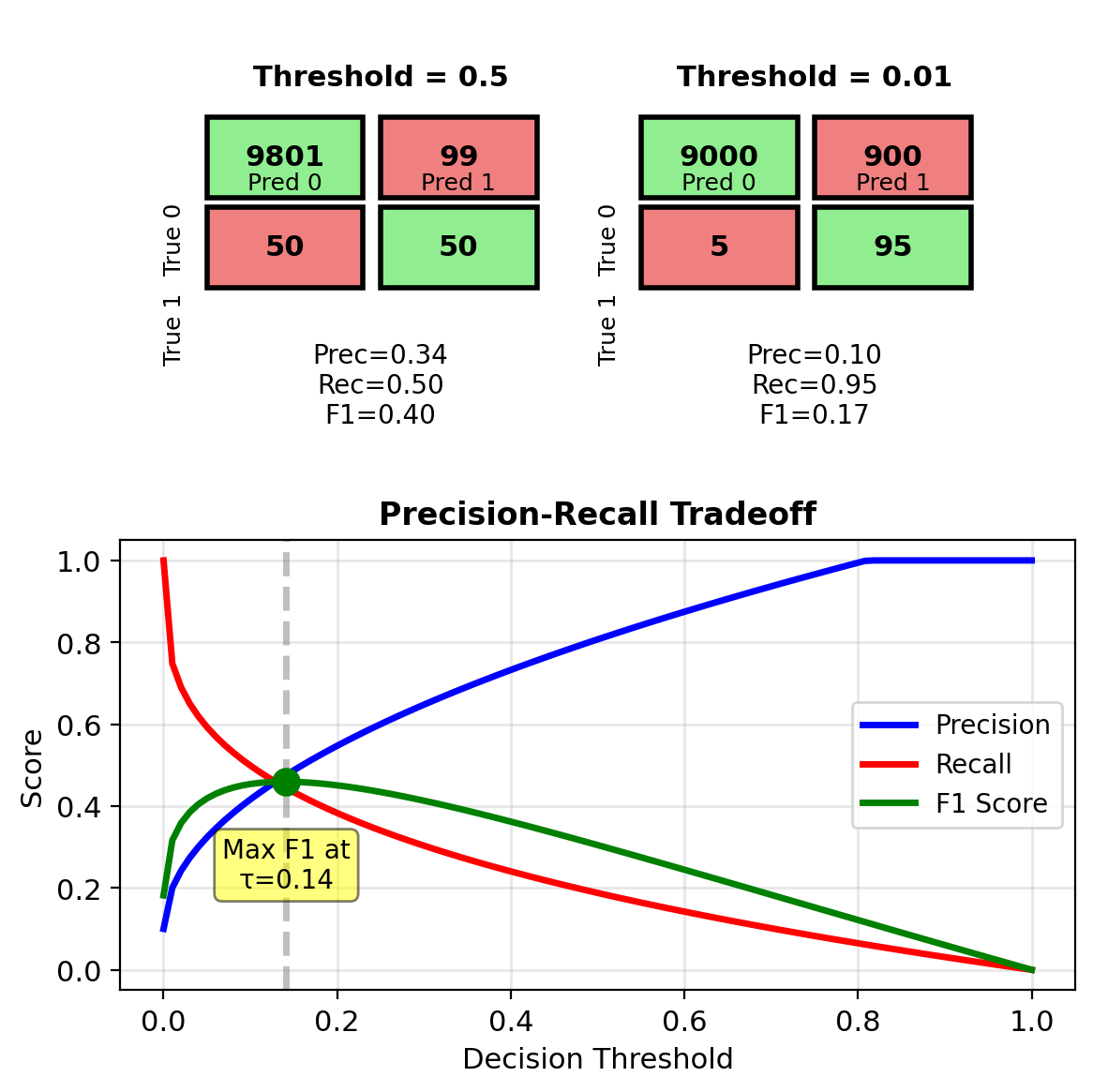
Class Imbalance and Costs
Imbalanced data: 99% negative, 1% positive
Problem with accuracy:
- Trivial classifier (always predict negative): 99% accurate
- Does not detect rare positive cases
Metrics for imbalanced data:
Precision: Of predicted positives, how many correct? \[\text{Precision} = \frac{\text{TP}}{\text{TP} + \text{FP}}\]
Recall (Sensitivity): Of true positives, how many found? \[\text{Recall} = \frac{\text{TP}}{\text{TP} + \text{FN}}\]
F1 Score: Harmonic mean \[F_1 = \frac{2 \cdot \text{Precision} \cdot \text{Recall}}{\text{Precision} + \text{Recall}}\]
Connection to costs: Optimize threshold based on \[\tau^* = \frac{c_{01} \cdot (1-\pi)}{c_{01}(1-\pi) + c_{10} \cdot \pi}\]
where \(\pi\) = class prior P(y=1)
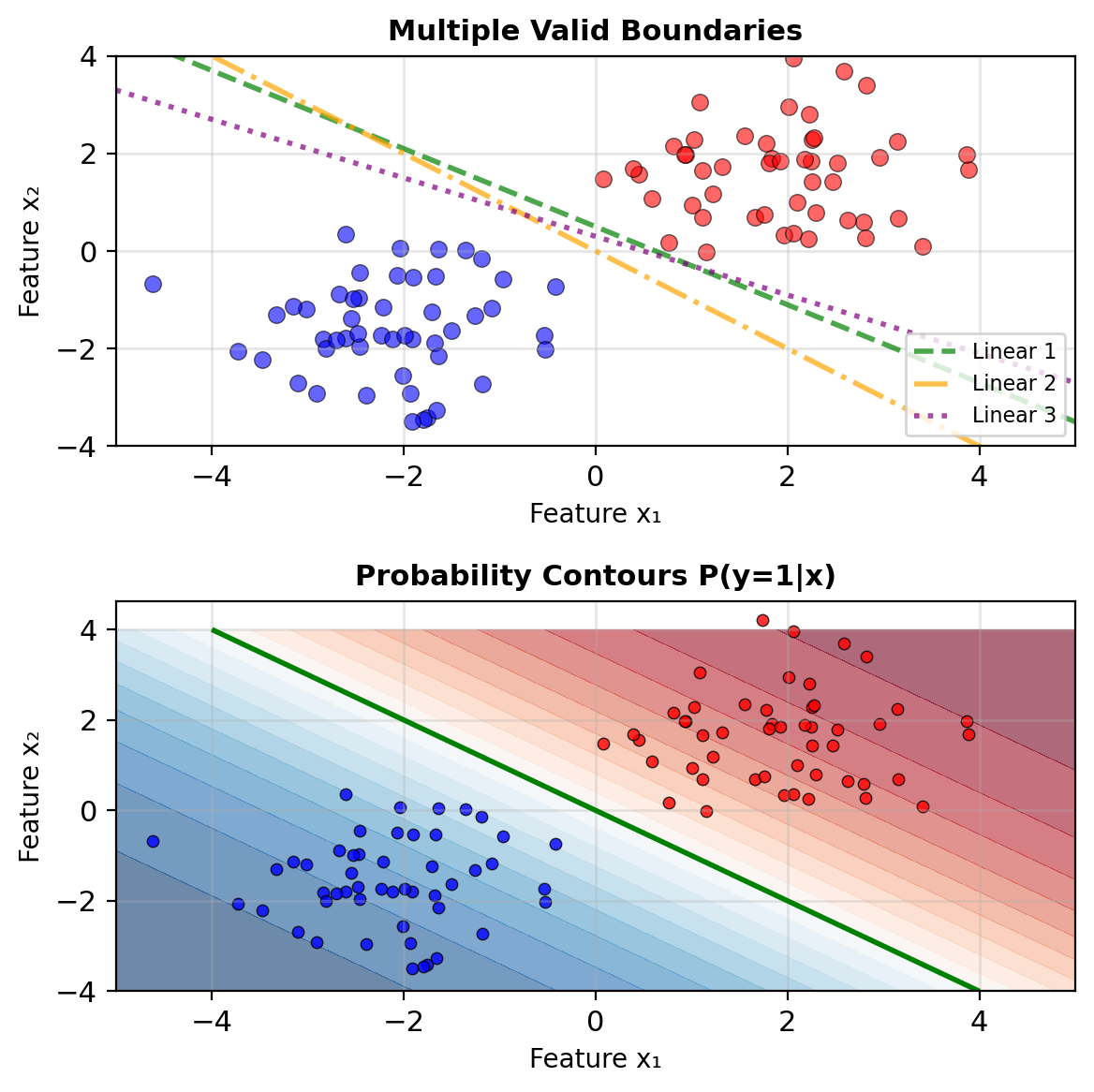
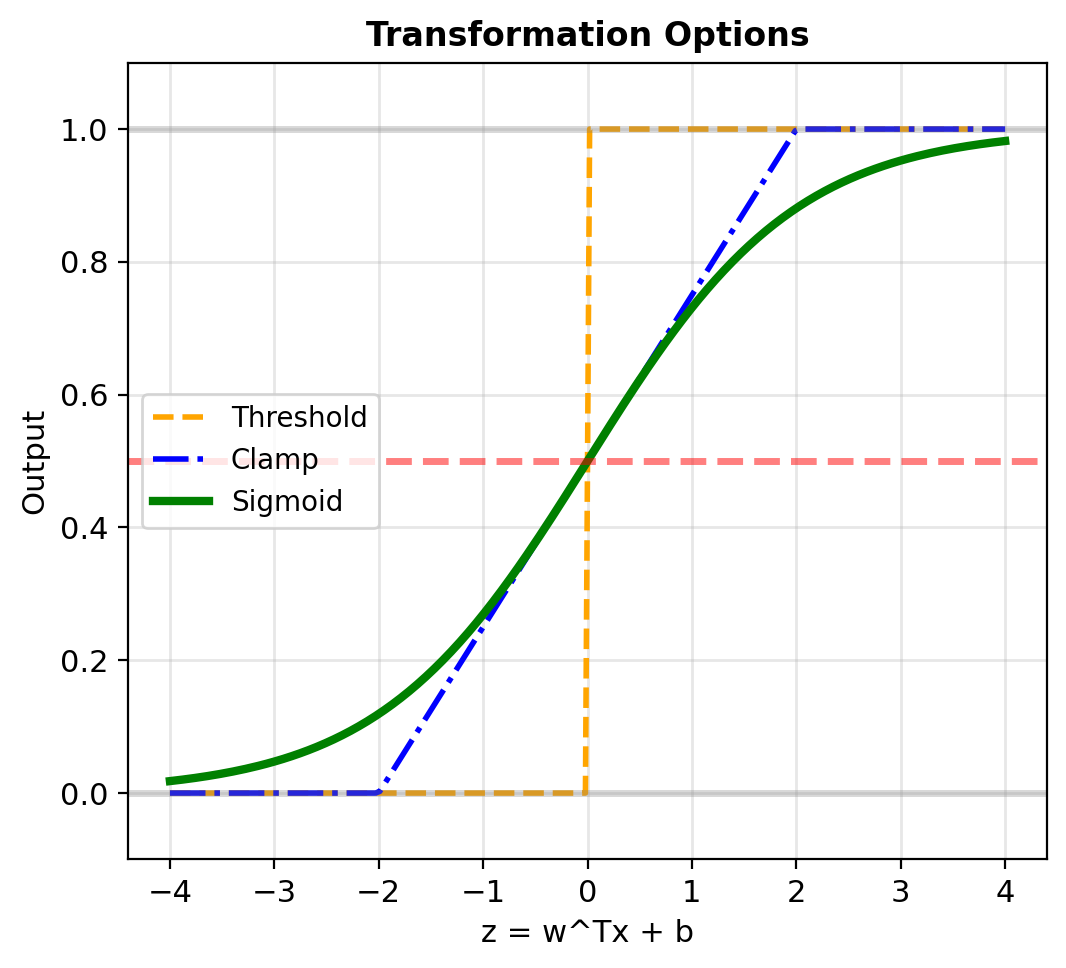
From Linear to Logistic
Why Linear Models Fail
Try modeling probability directly: \[p(\mathbf{x}) = \mathbf{w}^T\mathbf{x} + b\]
With \(w = 0.3\), \(b = 0.5\):
- \(p(x=-2) = -0.1\) (invalid)
- \(p(x=0) = 0.5\)
- \(p(x=2) = 1.1\) (invalid)
Problem: Linear outputs \(\in (-\infty, \infty)\) but probabilities need \(\in [0, 1]\)
Need transformation \(\mathbb{R} \to [0, 1]\) that:
- Outputs valid probabilities
- Preserves linear decision boundaries
- Is differentiable for optimization
Candidates:
- Threshold: \(p = \mathbb{1}[z > 0]\)
- Clamp: \(p = \max(0, \min(1, z))\) – Not differentiable
- Sigmoid: \(p = \frac{1}{1 + e^{-z}}\)
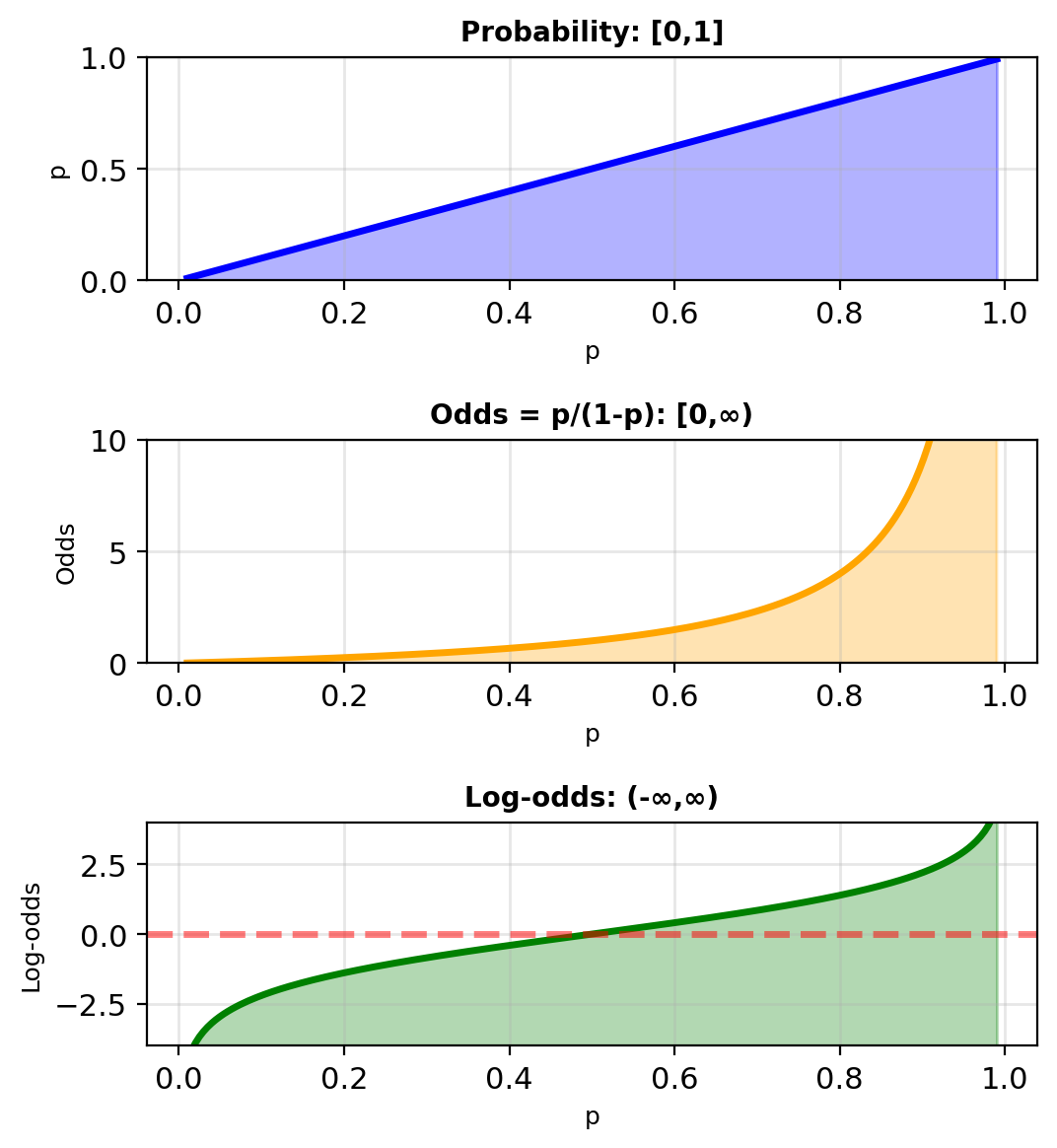
Modeling Log-Odds
Odds: Alternative to probability
\[\text{Odds}(A) = \frac{P(A)}{P(A^C)}\]
For binary outcome
\[\text{Odds} = \frac{p}{1-p} = \frac{P(y=1)}{P(y=0)}\]
Examples:
- \(p = 0.5\): Odds = 1 (1:1, “even odds”)
- \(p = 0.75\): Odds = 3 (3:1 in favor)
- \(p = 0.25\): Odds = 1/3 (1:3 against)
Range: \([0, \infty)\)
Log-odds (logit): \[\text{logit}(p) = \log\left(\frac{p}{1-p}\right)\]
Range: \((-\infty, \infty)\)
The Logistic Model
Model log-odds linearly: \[\log\left(\frac{p(\mathbf{x})}{1-p(\mathbf{x})}\right) = \mathbf{w}^T\mathbf{x} + b\]
Solving for \(p(\mathbf{x})\):
Let \(z = \mathbf{w}^T\mathbf{x} + b\)
\[\frac{p}{1-p} = e^z\]
\[p = (1-p)e^z\]
\[p = e^z - pe^z\]
\[p(1 + e^z) = e^z\]
\[p = \frac{e^z}{1 + e^z} = \frac{1}{1 + e^{-z}}\]
Gives the logistic (sigmoid) function
\[\boxed{p(\mathbf{x}) = \sigma(\mathbf{w}^T\mathbf{x} + b) = \frac{1}{1 + e^{-(\mathbf{w}^T\mathbf{x} + b)}}}\]
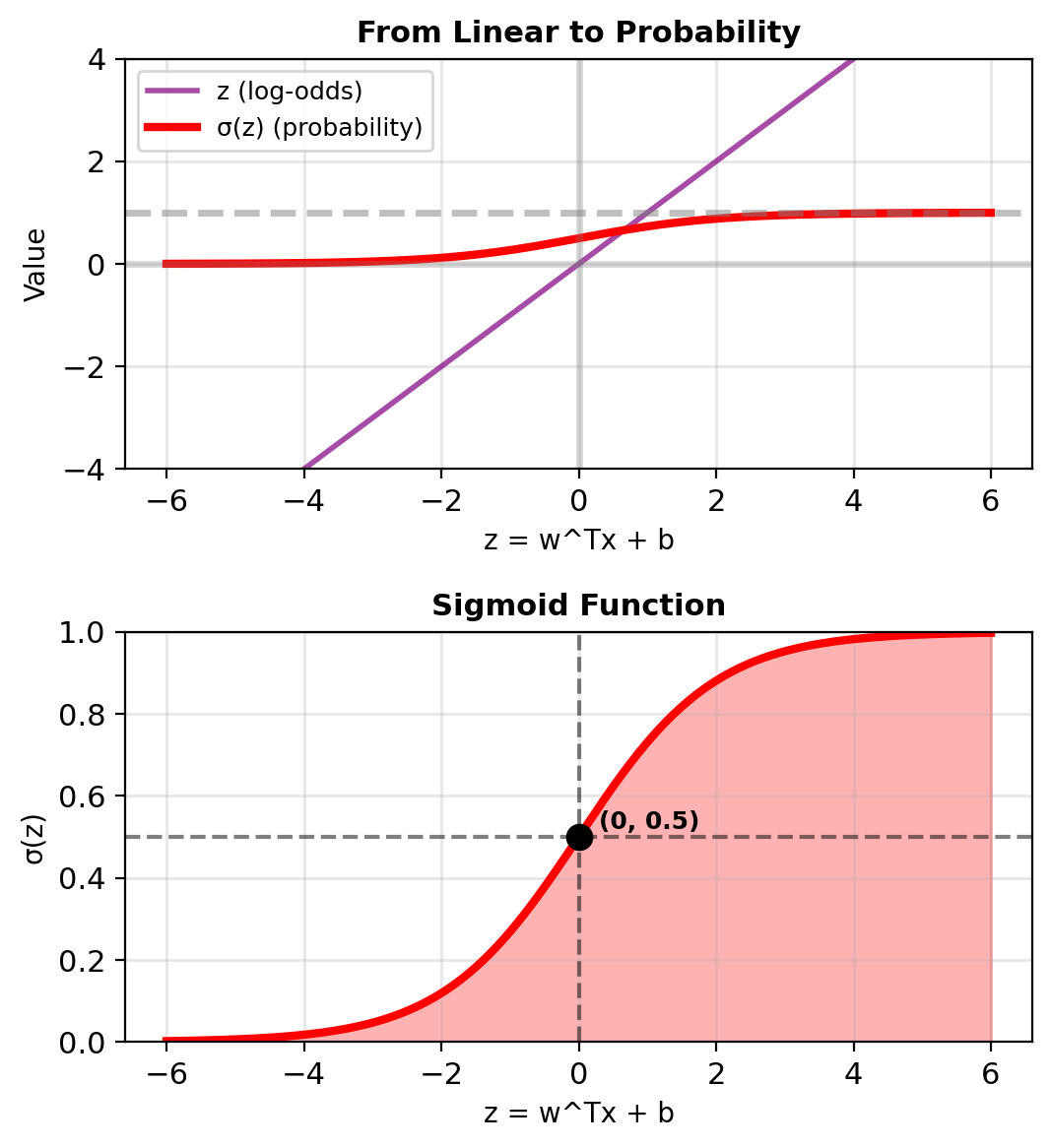
Connection to Linear Regression
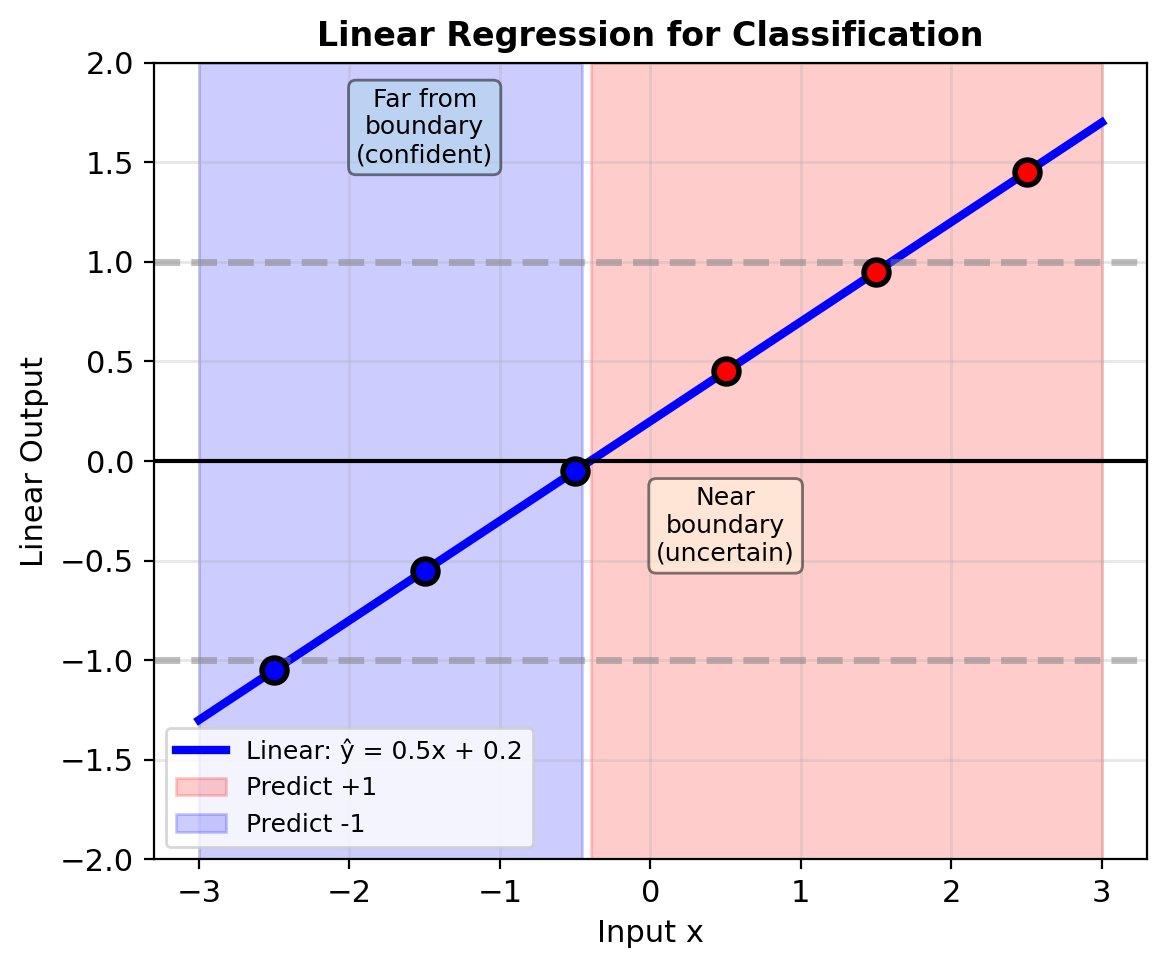
Recall: Linear regression for classification
\[\hat{y} = \mathbf{w}^T\mathbf{x} + b\]
with targets \(y \in \{-1, +1\}\) and hard decision: \[\text{class} = \text{sign}(\hat{y})\]
Linear regression gives:
- Linear decision boundary: \(\mathbf{w}^T\mathbf{x} + b = 0\)
- Distance from boundary: \(|\mathbf{w}^T\mathbf{x} + b|/\|\mathbf{w}\|\)
- Works well when classes are linearly separable
The problem:
- Output \(\hat{y} \in \mathbb{R}\) isn’t a probability
- No confidence measure
- Can’t handle varying misclassification costs
What we need: Convert \(\mathbf{w}^T\mathbf{x} + b\) to probability \(p \in [0,1]\)
Need smooth function: \(\mathbb{R} \to [0, 1]\)
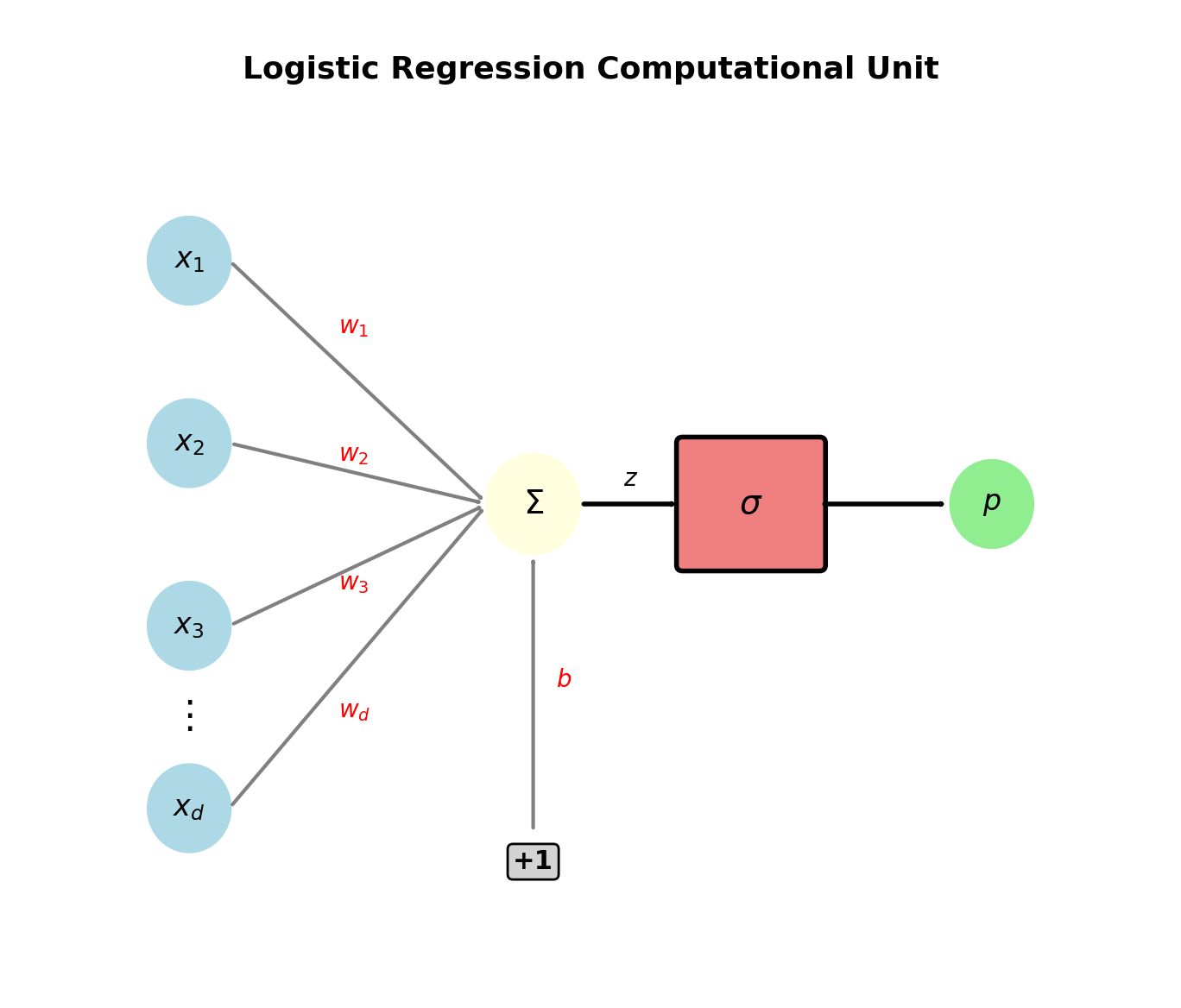
The Sigmoid Unit
Inputs: \(\mathbf{x} = [x_1, x_2, \ldots, x_d]^T\)
Weights: \(\mathbf{w} = [w_1, w_2, \ldots, w_d]^T\)
Bias: \(b\)
Linear combination: \[z = \mathbf{w}^T\mathbf{x} + b = \sum_{j=1}^d w_j x_j + b\]
Activation function: \[p = \sigma(z) = \frac{1}{1 + e^{-z}}\]
Output: \(p = P[\text{class 1}] \in (0, 1)\)
Decision rule: Predict class 1 if \(p > 0.5\)
The Sigmoid Derivative: \(\sigma' = \sigma(1 - \sigma)\)
Start with: \(\sigma(z) = \frac{1}{1 + e^{-z}}\)
Apply chain rule: \[\frac{d\sigma}{dz} = \frac{d}{dz}\left[(1 + e^{-z})^{-1}\right]\]
\[= -1 \cdot (1 + e^{-z})^{-2} \cdot \frac{d}{dz}(1 + e^{-z})\]
\[= -1 \cdot (1 + e^{-z})^{-2} \cdot (-e^{-z})\]
\[= \frac{e^{-z}}{(1 + e^{-z})^2}\]
Rewriting: \[= \frac{1}{1 + e^{-z}} \cdot \frac{e^{-z}}{1 + e^{-z}}\]
\[= \sigma(z) \cdot \frac{e^{-z}}{1 + e^{-z}}\]
And: \[\frac{e^{-z}}{1 + e^{-z}} = \frac{1/e^z}{1/e^z + 1} = \frac{1}{1 + e^z}\]
This equals \(\sigma(-z) = 1 - \sigma(z)\)
Therefore: \[\boxed{\sigma'(z) = \sigma(z)(1 - \sigma(z))}\]
Properties:
- Maximum at \(z = 0\)
- \(\sigma'(0) = 0.25\)
- Symmetric around \(z = 0\)
- Vanishes as \(z \to \pm\infty\)
Computing \(p = \sigma(z)\) first gives derivative as \(p(1-p)\).
Why Log-Odds (Not Other Transformations)?
Other candidates that map \(\mathbb{R} \to [0,1]\):
Probit (cumulative normal): \[p = \Phi(z) = \int_{-\infty}^z \frac{1}{\sqrt{2\pi}}e^{-t^2/2}dt\]
- No closed form
- Derivative involves normal PDF
- Used in econometrics
Complementary log-log: \[p = 1 - e^{-e^z}\]
- Asymmetric
- Good for rare events
- Different tail behavior
Logistic function advantages:
- Natural interpretation: Log-odds are intuitive
- Simple derivative: \(\sigma'(z) = \sigma(z)(1-\sigma(z))\)
- Computational efficiency: Closed form everything
- Information theory: Maximizes entropy given constraints

Model Properties
The sigmoid function \(\sigma(z) = \frac{1}{1 + e^{-z}}\):
Valid probabilities: \(\sigma(z) \in (0, 1)\) always
Smooth and differentiable: \[\sigma'(z) = \sigma(z)(1 - \sigma(z))\]
Linear decision boundary:
- Predict 1 if \(p > 0.5\)
- This occurs when \(\mathbf{w}^T\mathbf{x} + b > 0\)
- Boundary: \(\mathbf{w}^T\mathbf{x} + b = 0\) (hyperplane)
Interpretable coefficients:
- \(w_j\) = change in log-odds per unit \(x_j\)
- \(e^{w_j}\) = odds multiplication factor

From Model to Learning
We have the model: \[P(y=1|\mathbf{x}) = \sigma(\mathbf{w}^T\mathbf{x} + b)\]
Now need to learn parameters \(\mathbf{w}, b\)
Given training data: \(\mathcal{D} = \{(\mathbf{x}_i, y_i)\}_{i=1}^n\)
- \(\mathbf{x}_i \in \mathbb{R}^d\): features
- \(y_i \in \{0, 1\}\): labels
Objective: Maximum likelihood
- Find parameters that maximize \(P(\mathcal{D}|\mathbf{w}, b)\)
- Equivalent to minimizing cross-entropy loss
Maximum Likelihood Principle
Finding best parameters: Maximum Likelihood Estimation
Recall: If uniform prior, MAP is MLE: \[\hat{\mathbf{w}} = \arg\max_{\mathbf{w}} P(\text{data}|\mathbf{w})\]
“Find parameters that make observed data most probable”
Why MLE?
- Consistent: Converges to true value as \(n \to \infty\)
- Efficient: Achieves lowest possible variance
- Invariant: Same under reparameterizations
- Information-theoretic: Minimizes KL divergence
For regression: Gaussian noise → squared loss
For classification:
- Each \(y_i\) follows Bernoulli(\(p_i\))
- Need to model \(p(\mathbf{x}) \in [0,1]\)
Likelihood: \[P(\text{data}|\mathbf{w}) = \prod_{i=1}^n P(y_i|\mathbf{x}_i, \mathbf{w})\]
Bernoulli Model for Binary Data
Suppose each observation \(y_i \in \{0, 1\}\) is Bernoulli (coin flip): \[P(y_i = 1 | \mathbf{x}_i) = p(\mathbf{x}_i)\] \[P(y_i = 0 | \mathbf{x}_i) = 1 - p(\mathbf{x}_i)\]
Therefore: \[P(y_i | \mathbf{x}_i) = p(\mathbf{x}_i)^{y_i} (1-p(\mathbf{x}_i))^{1-y_i}\]
Check:
- If \(y_i = 1\): \(p^1 (1-p)^0 = p\)
- If \(y_i = 0\): \(p^0 (1-p)^1 = 1-p\)
Likelihood for all data (independence assumption): \[\mathcal{L}(\mathbf{w}) = \prod_{i=1}^n p_i^{y_i} (1-p_i)^{1-y_i}\]
where \(p_i = p(\mathbf{x}_i; \mathbf{w})\)
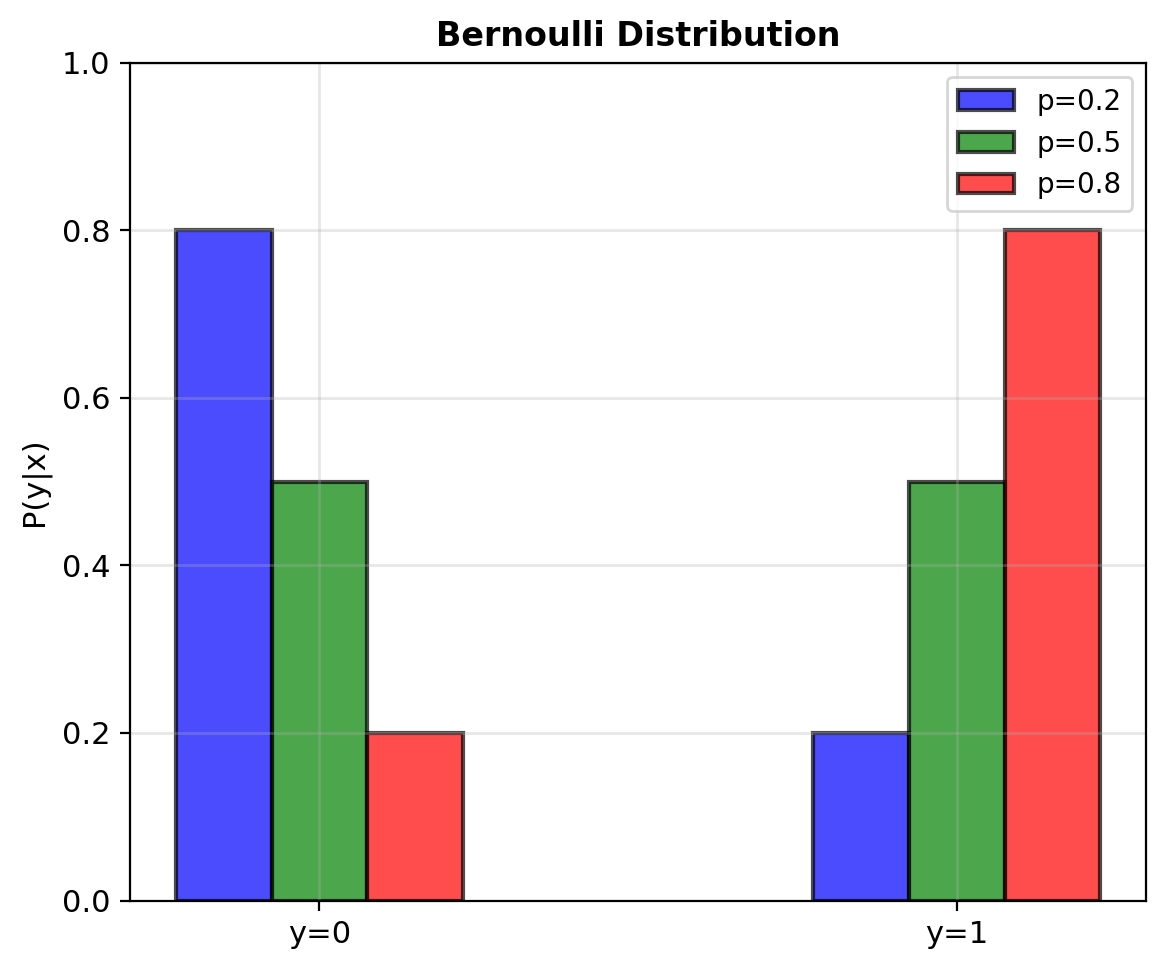
Requirement: Must have \(0 \leq p(\mathbf{x}) \leq 1\)
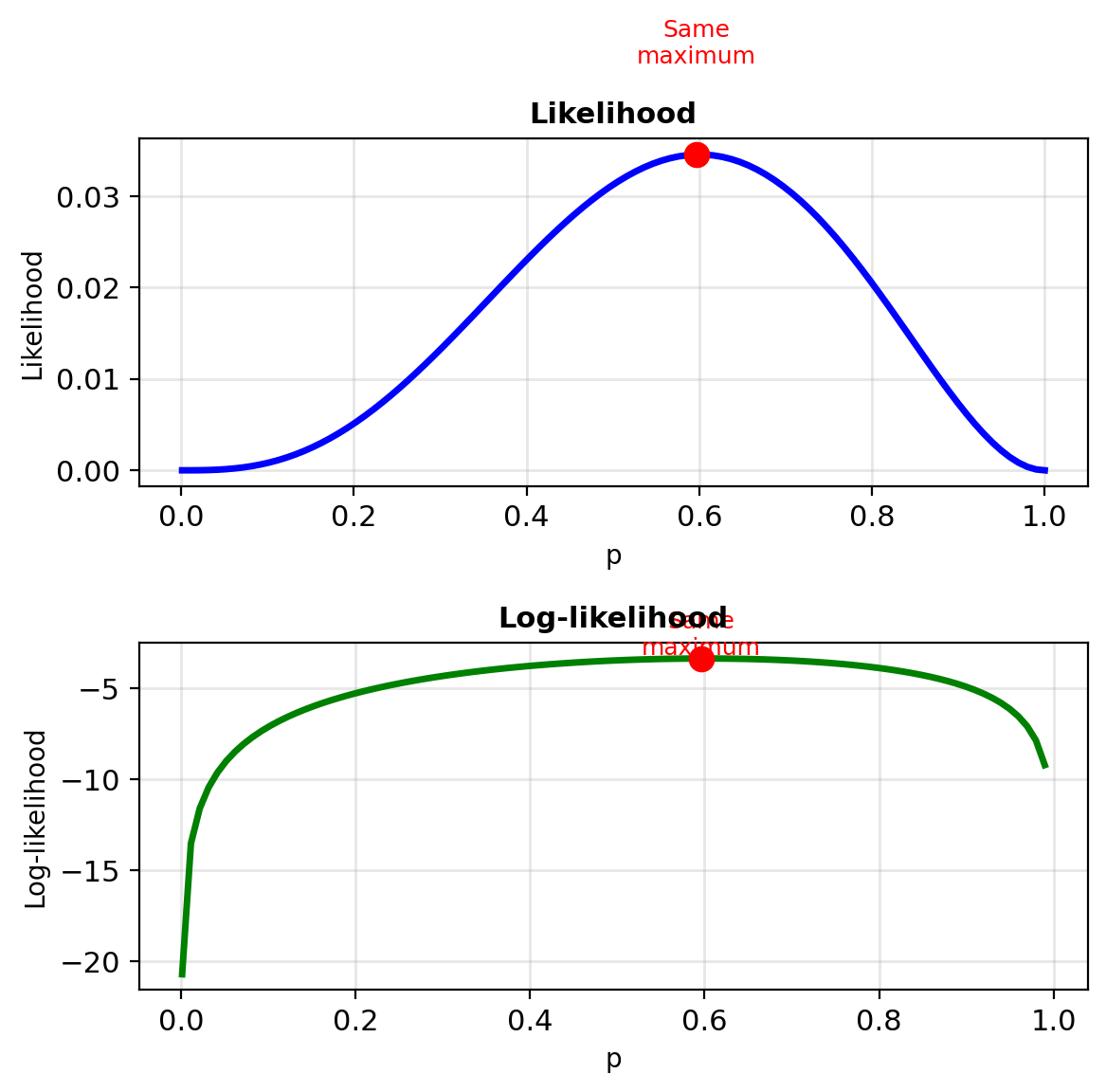
Taking the Logarithm
Logarithm converts products to sums: \[\log \mathcal{L} = \sum_{i=1}^n [y_i \log p_i + (1-y_i)\log(1-p_i)]\]
Why log?
- Converts products to sums
- Numerically stable
- Same maximum (log is monotonic)
- Derivatives are simpler
Maximizing log-likelihood = Minimizing negative log-likelihood: \[\text{NLL} = -\sum_{i=1}^n [y_i \log p_i + (1-y_i)\log(1-p_i)]\]
This equals binary cross-entropy loss
Gradient for Binary Cross-Entropy
Log-likelihood: \[\ell = \sum_{i=1}^n [y_i \log p_i + (1-y_i)\log(1-p_i)]\]
where \(p_i = \sigma(\mathbf{w}^T\mathbf{x}_i + b)\)
Taking derivative (using chain rule): \[\frac{\partial \ell_i}{\partial z_i} = y_i - p_i\]
Therefore: \[\frac{\partial \ell}{\partial \mathbf{w}} = \sum_{i=1}^n (y_i - p_i)\mathbf{x}_i\]
\[\frac{\partial \ell}{\partial b} = \sum_{i=1}^n (y_i - p_i)\]
Elegant result: Gradient is sum of (error × feature)

Misclassified points contribute most to gradient
Logistic Regression Algorithm
Model: \(p = \sigma(\mathbf{w}^T\mathbf{x} + b)\)
Objective: Maximize log-likelihood \[\ell = \sum_{i=1}^n [y_i \log p_i + (1-y_i)\log(1-p_i)]\]
Gradient: \[\nabla_\mathbf{w} \ell = \mathbf{X}^T(\mathbf{y} - \mathbf{p})\]
Update: Gradient ascent \[\mathbf{w} \leftarrow \mathbf{w} + \eta \nabla_\mathbf{w} \ell\]
Converge: When \(||\nabla \ell|| < \epsilon\)
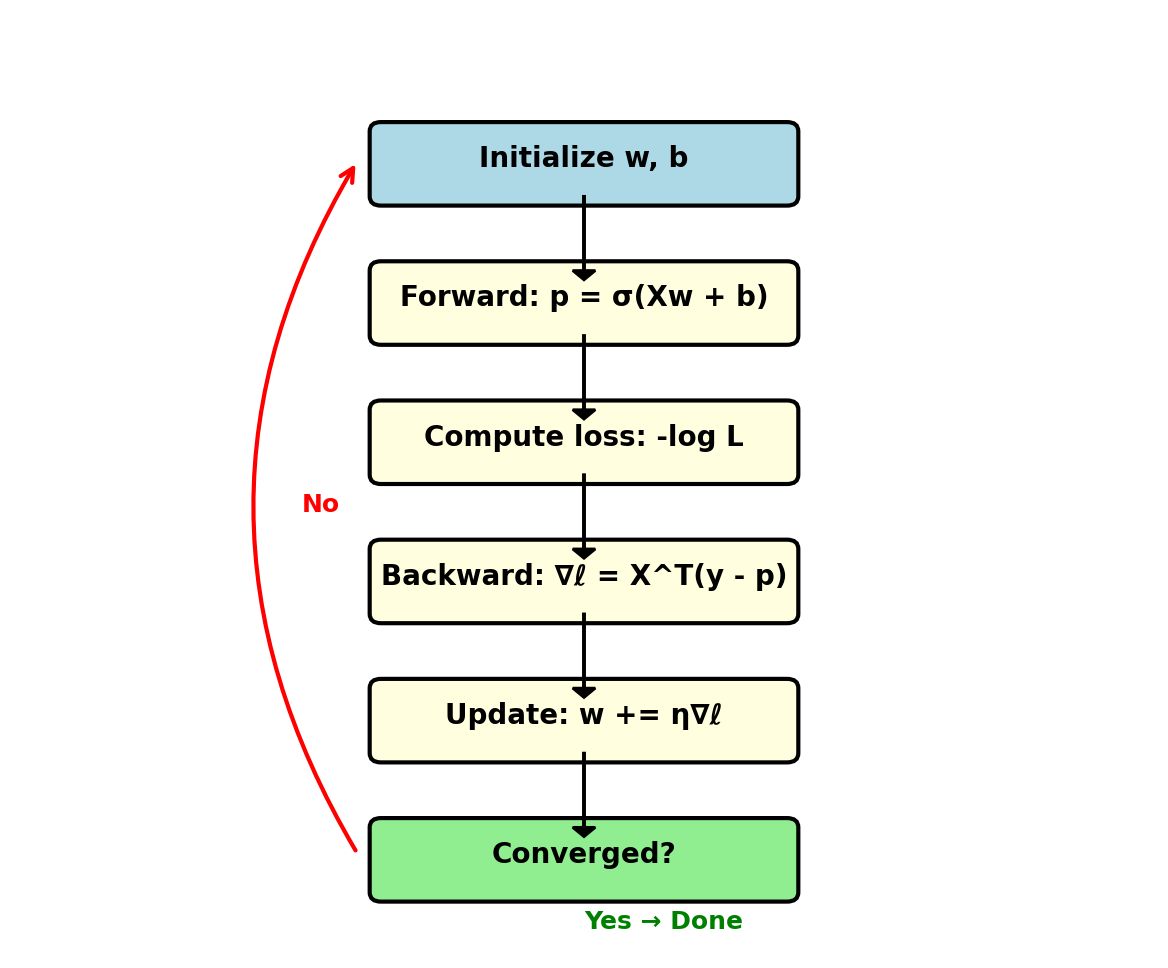
Iterate until convergence (typical, 100s of steps)
Example: Spam Detection
Problem: Classify emails as spam or legitimate
Features extracted from email:
- Word frequencies: “FREE”, “CLICK”, “offer”
- Sender reputation score
- Number of ALL CAPS words
- Exclamation marks count
- Links to external domains
- Time of day sent
Example vector \(\mathbf{x} \in \mathbb{R}^6\):
Email: "FREE OFFER! Click HERE!!!"
x = [2, 0.1, 2, 3, 1, 0.3]
↑ ↑ ↑ ↑ ↑ ↑
FREE low 2 3 1 3am
offer rep CAPS !! linkGoal: Learn \(P(\text{spam}|\mathbf{x})\)
Spam filters use 1000s of features
Feature Engineering for Spam Detection
Converting email → numbers:
1. Bag of words (simple counts):
vocab = ["free", "click", "meeting", "report"]
email = "free click click"
x = [1, 2, 0, 0] # Counts per vocabulary word2. TF-IDF (weighted by rarity):
# Term Frequency × Inverse Document Frequency
tfidf(word) = count(word) × log(N/df(word))
# Rare words get higher weight3. Domain-specific features:
- Sender in contacts? → 0 or 1
- Previous emails from sender → count
- Contains attachments → 0 or 1
- HTML/text ratio → [0, 1]
Feature vector: \(\mathbf{x} \in \mathbb{R}^d\), e.g., \(d\) = 100-10,000
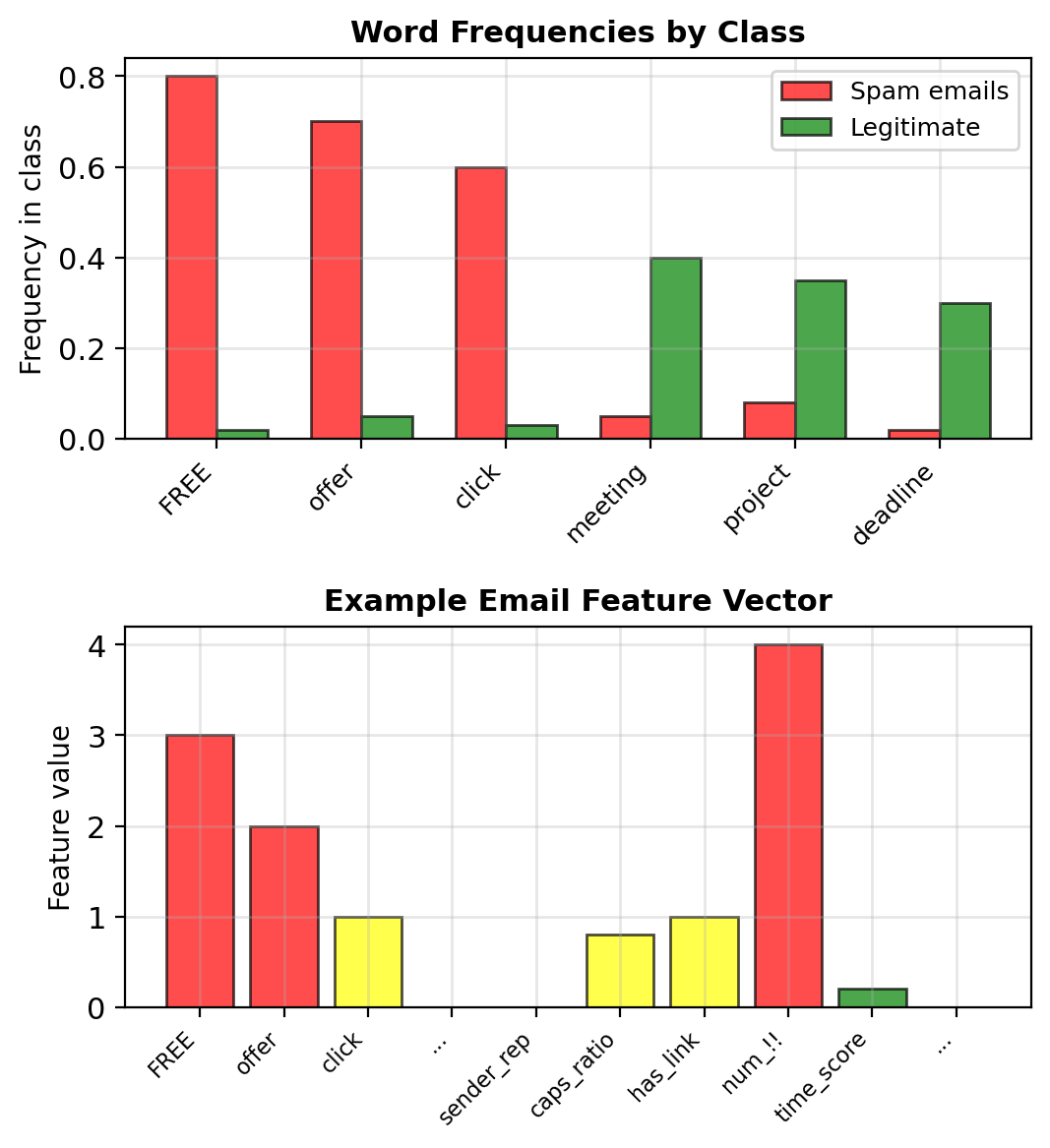
High values in red features → likely spam
Training Dataset Structure
Dataset: \(n\) = 10,000 labeled emails
# Each email becomes a feature vector
X = np.array([
[3, 2, 1, ..., 0.1], # spam
[0, 0, 0, ..., 0.9], # legitimate
[2, 1, 3, ..., 0.2], # spam
...
]) # Shape: (10000, 100)
y = np.array([1, 0, 1, ...]) # LabelsDifficult to balance:
- High recall: catch most spam
- Low false positive: don’t block legitimate
Metric: Precision at 95% recall
Target performance:
- Detection rate > 95%
- False positive rate < 0.1%
- Latency < 10ms per email
- Model size < 10MB
For instance: Identify 9,500/10,000 spam with ≤6 legitimate emails blocked
Example class distribution:
- Spam: 40% (4,000 emails)
- Legitimate: 60% (6,000 emails)

Training Logistic Regression
Model: \[P(\text{spam}|\mathbf{x}) = \sigma(\mathbf{w}^T\mathbf{x} + b)\]
Training (gradient ascent on log-likelihood):
# Initialize
w = np.random.randn(100) * 0.01
b = 0
for epoch in range(100):
# Compute predictions
z = X @ w + b
p = sigmoid(z)
# Gradient step
grad_w = X.T @ (y - p) / n
grad_b = np.mean(y - p)
w += learning_rate * grad_w
b += learning_rate * grad_bLearned weights reveal spam indicators:
- \(w_{\text{FREE}} = 2.3\) (strong spam signal)
- \(w_{\text{meeting}} = -1.8\) (legitimate signal)
- \(w_{\text{sender_rep}} = -3.1\) (reputation matters)
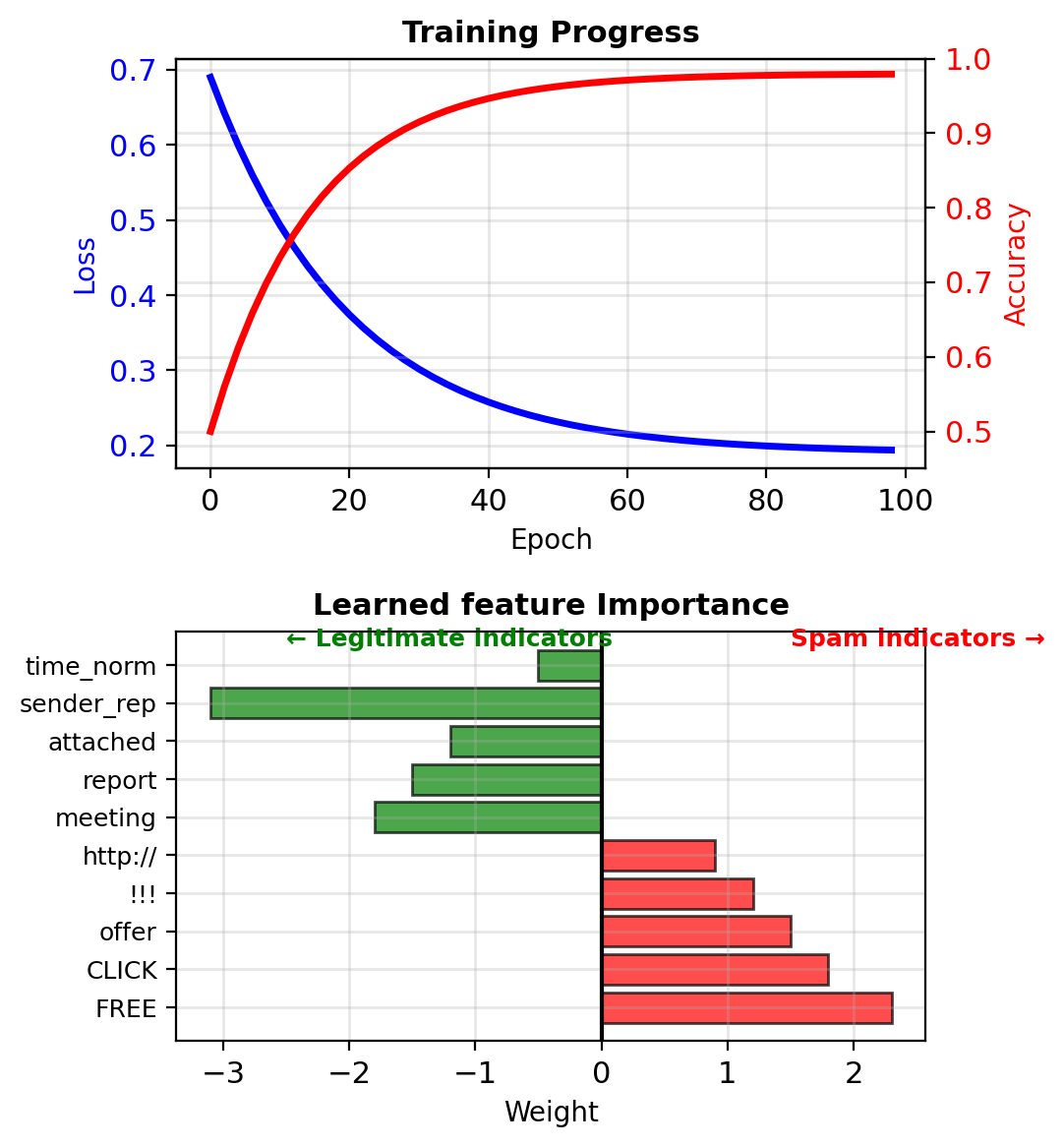
Logistic Performance - Single sample
Same data, logistic model:
With \(w = 1.5\), \(b = 0\):
Computing \(p(x) = \frac{1}{1 + e^{-(wx + b)}}\):
- \(z_1 = 1.5(-2) = -3\), \(p_1 = \sigma(-3) = 0.047\)
- \(z_2 = 1.5(-1) = -1.5\), \(p_2 = \sigma(-1.5) = 0.182\)
- \(z_3 = 1.5(0) = 0\), \(p_3 = \sigma(0) = 0.5\)
- \(z_4 = 1.5(1) = 1.5\), \(p_4 = \sigma(1.5) = 0.818\)
- \(z_5 = 1.5(2) = 3\), \(p_5 = \sigma(3) = 0.953\)
All valid probabilities!

Log-likelihood: \[\ell = \sum_{i=1}^5 [y_i \log p_i + (1-y_i)\log(1-p_i)]\]
Inference Performance
Inference for new email:
def classify_email(email_text, w, b):
# Extract features
x = extract_features(email_text)
# Compute probability
z = np.dot(w, x) + b
p_spam = sigmoid(z)
# Decision with threshold
if p_spam > 0.95: # High threshold
return "spam", p_spam
else:
return "legitimate", p_spamExample performance:
- Accuracy: 97.2%
- Spam recall: 95.1%
- False positive rate: 0.08%
- Inference time: 0.3ms per email
- Model size: 100 × 8 bytes = 800B
Advantages:
- Interpretable: see why email flagged
- Fast: millions of emails per second
- Updatable: online learning for new spam
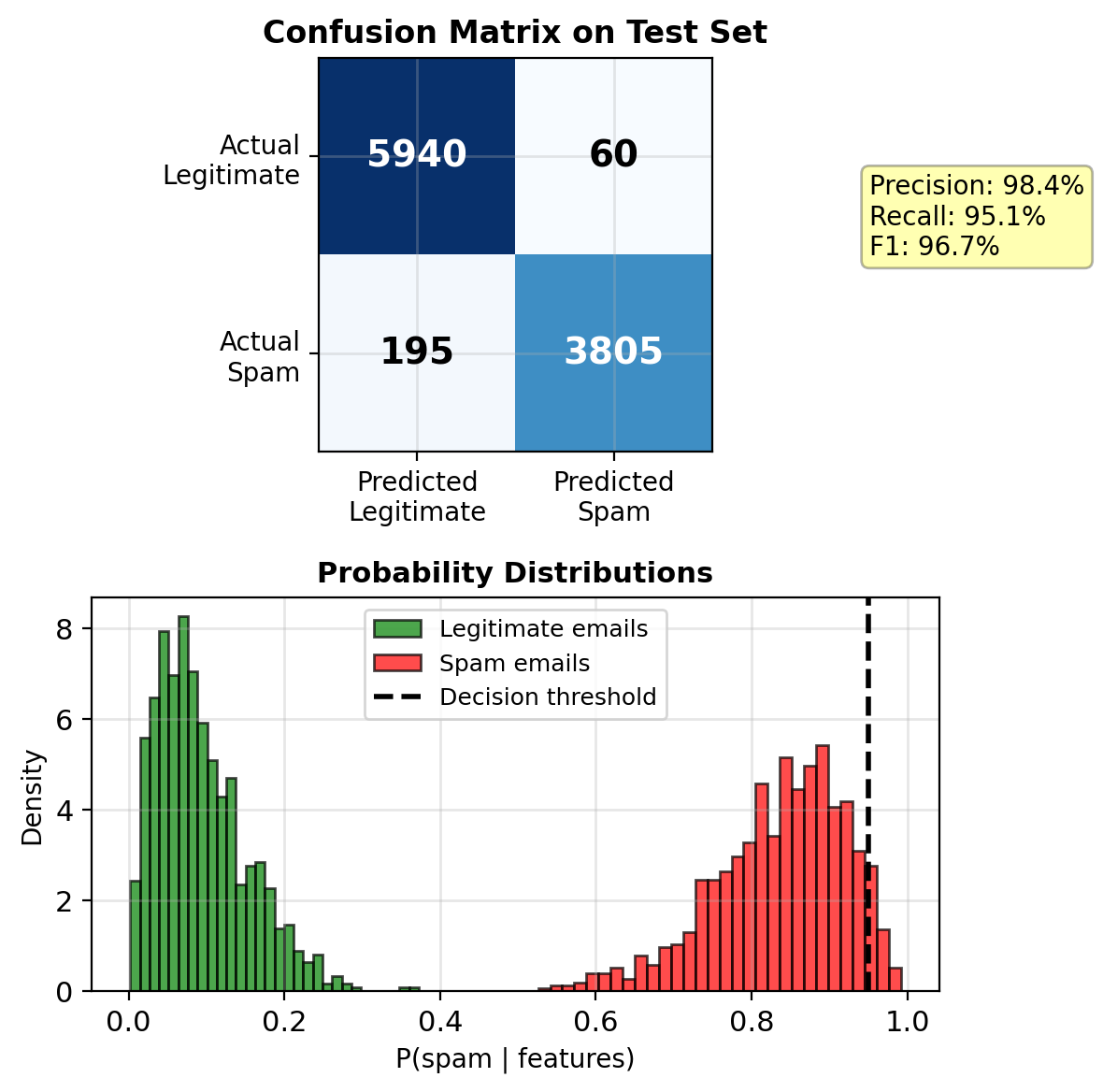
Threshold tuning possible since calibrated probabilities
Logistic Regression Components
Linear model: \[z = \mathbf{w}^T\mathbf{x} + b \in \mathbb{R}\]
Sigmoid transform: \[p = \sigma(z) = \frac{1}{1 + e^{-z}} \in (0,1)\]
Logistic regression: \[P(y=1|\mathbf{x}) = \sigma(\mathbf{w}^T\mathbf{x} + b)\]
Optimize by maximizing log-likelihood: \[\max_{\mathbf{w},b} \sum_{i=1}^n [y_i \log p_i + (1-y_i)\log(1-p_i)]\]
Gradient: \[\nabla_\mathbf{w} \ell = \sum_{i=1}^n (y_i - p_i)\mathbf{x}_i\]

Maximum Likelihood Estimation
Maximum Likelihood From Bayes
Bayes theorem for weights (i.e., parameters): \[P(\mathbf{w}|\mathcal{D}) = \frac{P(\mathcal{D}|\mathbf{w})P(\mathbf{w})}{P(\mathcal{D})}\]
Maximum a posteriori (MAP): \[\hat{\mathbf{w}}_{\text{MAP}} = \arg\max_{\mathbf{w}} \frac{P(\mathcal{D}|\mathbf{w})P(\mathbf{w})}{P(\mathcal{D})} = \arg\max_{\mathbf{w}} P(\mathcal{D}|\mathbf{w})P(\mathbf{w})\]
With uniform prior \(P(\mathbf{w}) = \text{const}\), so: \[\hat{\mathbf{w}}_{\text{MLE}} = \arg\max_{\mathbf{w}} P(\mathcal{D}|\mathbf{w})\]
For classification data \(\mathcal{D} = \{(\mathbf{x}_i, y_i)\}_{i=1}^n\):
Assuming independent observations: \[P(\mathcal{D}|\mathbf{w}) = \prod_{i=1}^n P(y_i|\mathbf{x}_i, \mathbf{w})\]
With Bernoulli model: \[= \prod_{i=1}^n p_i^{y_i}(1-p_i)^{1-y_i}\]
where \(p_i = \sigma(\mathbf{w}^T\mathbf{x}_i + b)\)
Log-likelihood (sums replace products): \[\ell(\mathbf{w}) = \sum_{i=1}^n [y_i \log p_i + (1-y_i)\log(1-p_i)]\]
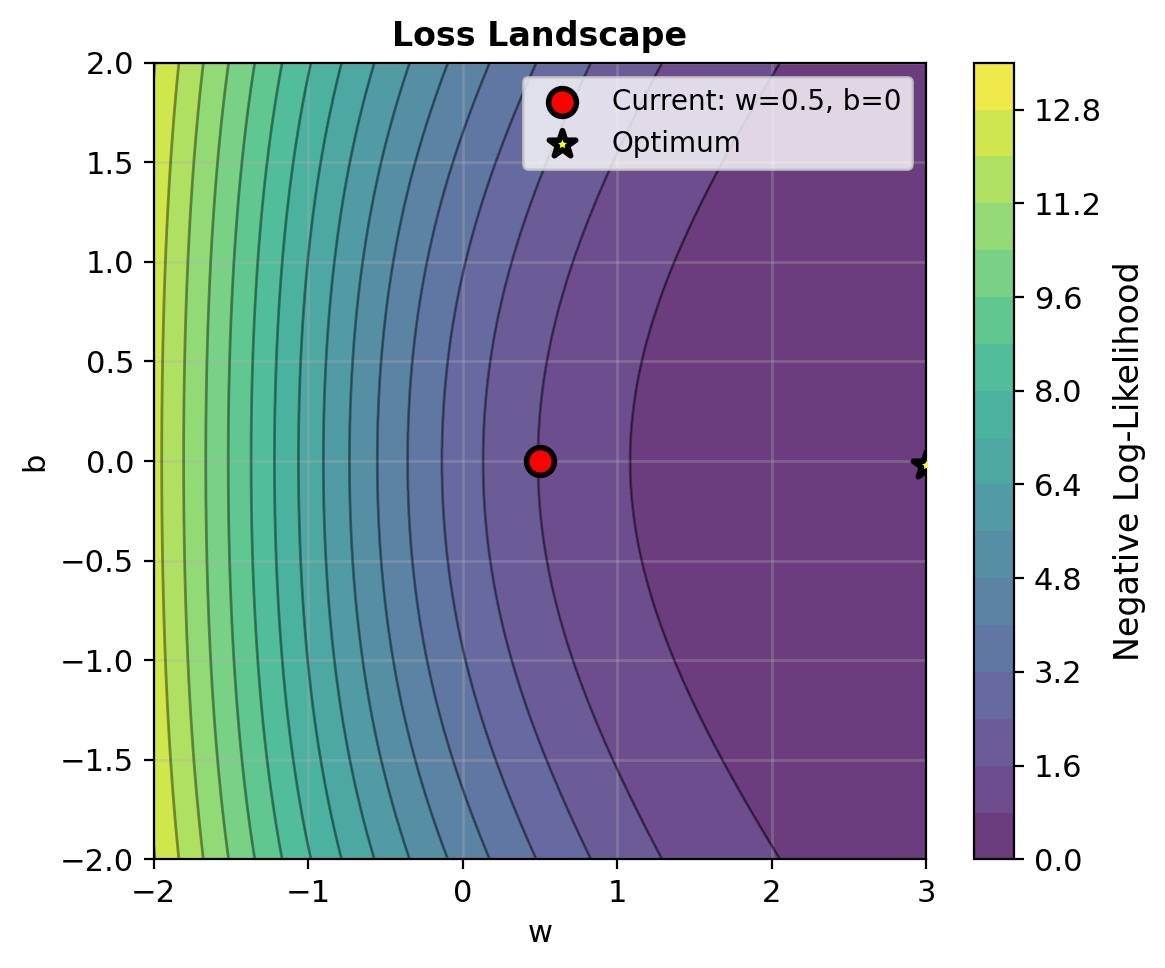
Example: MLE with 4 Points – Compute the Likelihood
Dataset: 4 points in 1D
Current Model: \(p(x) = \sigma(wx + b)\)
with \(w = 0.5\), \(b = 0\)
Compute predictions:
- \(z_1 = 0.5(-2) + 0 = -1\), \(p_1 = \sigma(-1) = 0.27\)
- \(z_2 = 0.5(-1) + 0 = -0.5\), \(p_2 = \sigma(-0.5) = 0.38\)
- \(z_3 = 0.5(1) + 0 = 0.5\), \(p_3 = \sigma(0.5) = 0.62\)
- \(z_4 = 0.5(2) + 0 = 1\), \(p_4 = \sigma(1) = 0.73\)
Errors \(y - p\):
- Point 1: \(0 - 0.27 = -0.27\)
- Point 2: \(0 - 0.38 = -0.38\)
- Point 3: \(1 - 0.62 = +0.38\)
- Point 4: \(1 - 0.73 = +0.27\)
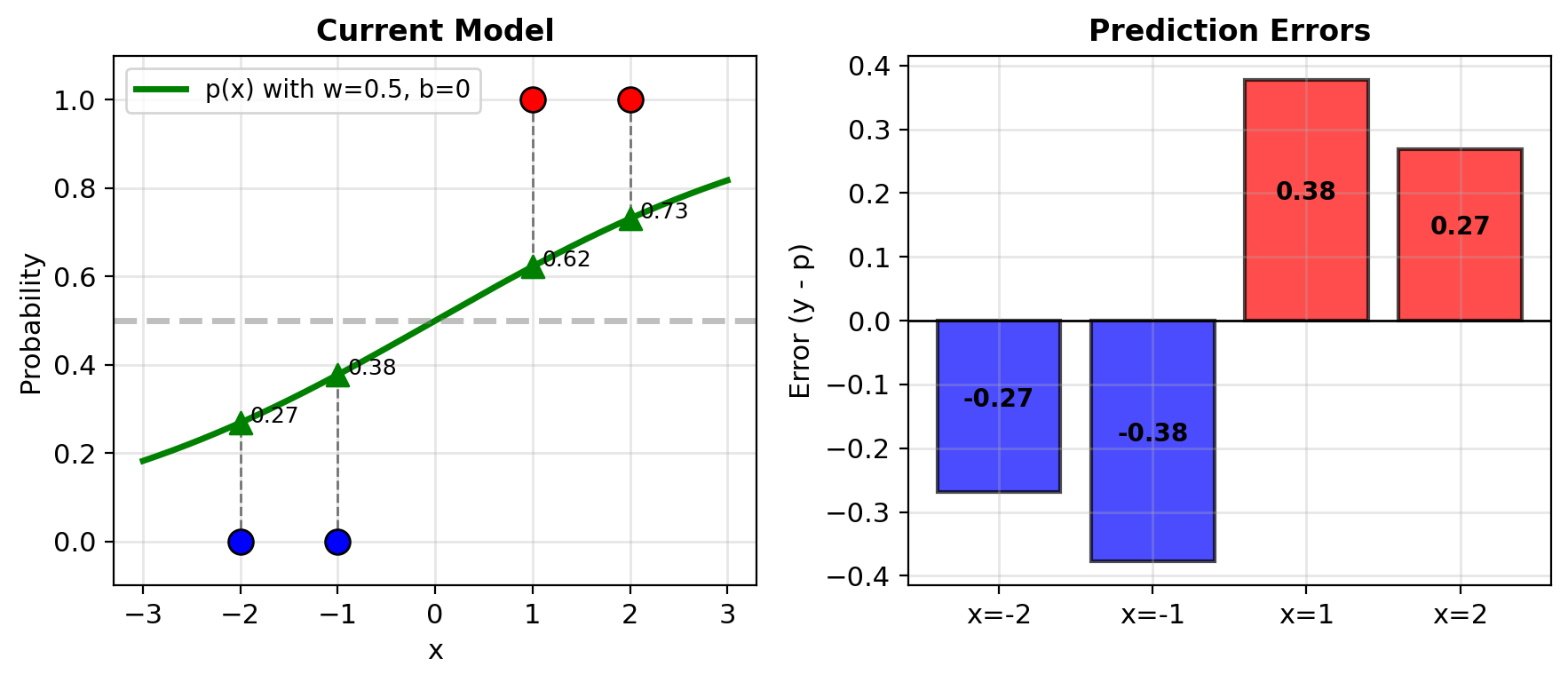
Compute the Log-Likelihood
Log-likelihood: \[\ell = \sum_{i=1}^4 [y_i \log p_i + (1-y_i)\log(1-p_i)]\]
So:
- \(i=1\): \(0 \cdot \log(0.27) + 1 \cdot \log(0.73) = -0.31\)
- \(i=2\): \(0 \cdot \log(0.38) + 1 \cdot \log(0.62) = -0.48\)
- \(i=3\): \(1 \cdot \log(0.62) + 0 \cdot \log(0.38) = -0.48\)
- \(i=4\): \(1 \cdot \log(0.73) + 0 \cdot \log(0.27) = -0.31\)
Total: \(\ell = -1.58\)
Negative log-likelihood: \(\text{NLL} = 1.58\)
Minimize this loss function
Compute the Gradient
Gradient formulas (from earlier): \[\frac{\partial \ell}{\partial w} = \sum_{i=1}^n (y_i - p_i)x_i\] \[\frac{\partial \ell}{\partial b} = \sum_{i=1}^n (y_i - p_i)\]
For our example:
\(\frac{\partial \ell}{\partial w}\): \[\begin{align} &= (-0.27)(-2) + (-0.38)(-1)\\ &\quad + (0.38)(1) + (0.27)(2)\\ &= 0.54 + 0.38 + 0.38 + 0.54\\ &= 1.84 \end{align}\]
\(\frac{\partial \ell}{\partial b}\): \[= -0.27 - 0.38 + 0.38 + 0.27 = 0\]
Computing contributions:
| \(i\) | \(x_i\) | \(y_i\) | \(p_i\) | \((y_i - p_i)x_i\) |
|---|---|---|---|---|
| 1 | -2 | 0 | 0.27 | 0.54 |
| 2 | -1 | 0 | 0.38 | 0.38 |
| 3 | 1 | 1 | 0.62 | 0.38 |
| 4 | 2 | 1 | 0.73 | 0.54 |
Sum: \(\nabla_w \ell = 1.84\)

Gradient w.r.t. \(w\) positive: increase \(w\)
Gradient w.r.t. \(b\) zero: \(b\) locally optimal
Larger errors \(|y_i - p_i|\) contribute more to gradient.
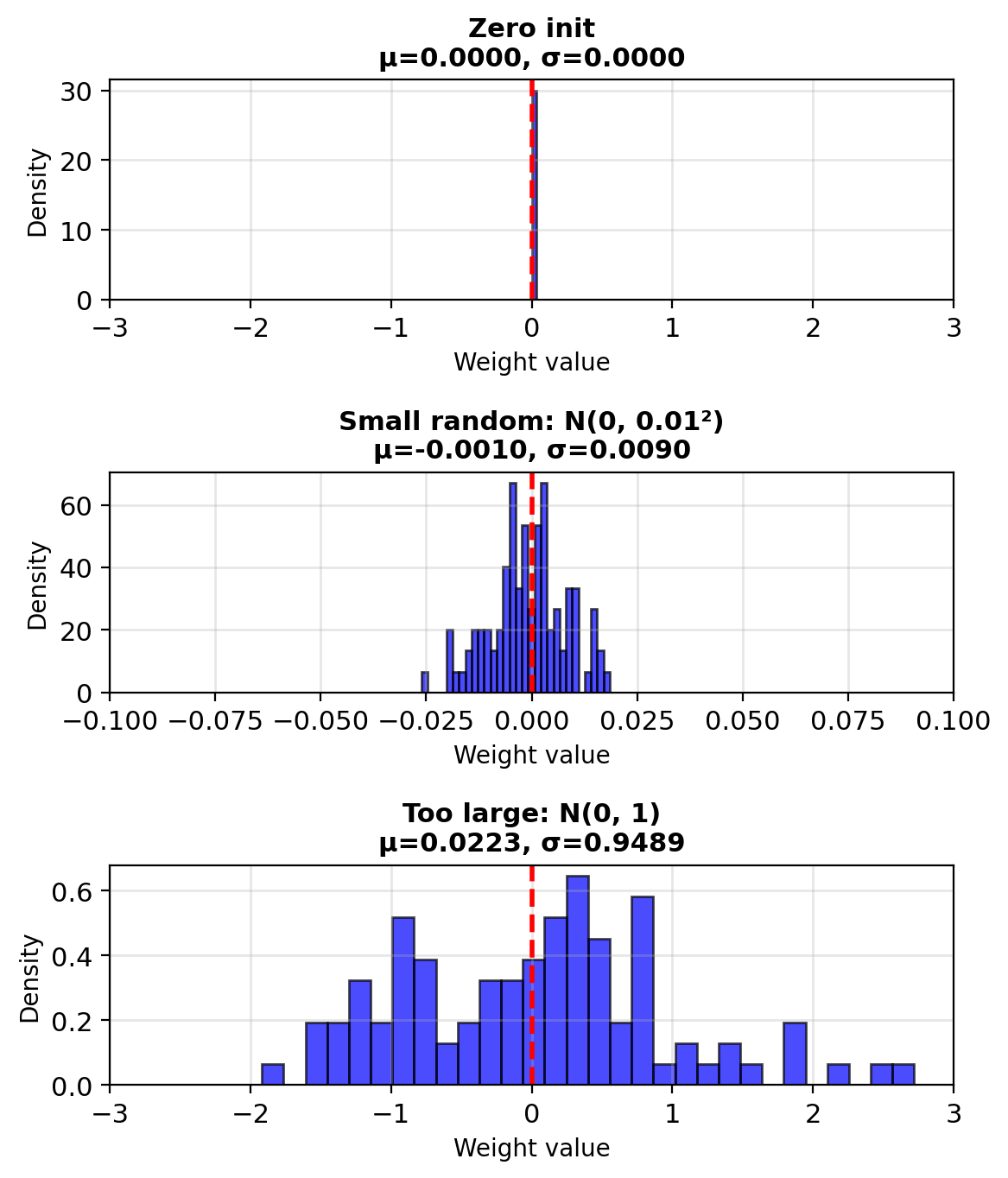
Initialize Weights Before Optimization
Standard initialization:
Why random: Zero works but random is standard
- Gradient: \(\nabla_\mathbf{w} \ell = \mathbf{X}^T(\mathbf{y} - \mathbf{p})\)
- Gradient depends only on data, not symmetry
- With \(\mathbf{w} = \mathbf{0}\): all predictions \(p_i = 0.5\)
- Works for logistic regression (unlike neural networks)
- Random initialization is standard practice
Why small (0.01 scale):
- Prevents sigmoid saturation: \(\sigma(z) \approx 0\) or \(1\) when \(|z|\) large
- Keeps gradients large: \(\sigma'(z) = \sigma(z)(1-\sigma(z))\) peaks at \(z=0\)
- Scale of 0.01 typical for normalized features
Gradient Descent — \(\nabla_\mathbf{w}\)
Update rule (minimize NLL): \[\mathbf{w}^{\text{new}} = \mathbf{w}^{\text{old}} + \eta \cdot \nabla \ell\]
Addition follows from maximizing log-likelihood (equivalent to subtracting gradient of NLL)
With learning rate \(\eta = 0.5\):
- \(w^{\text{new}} = 0.5 + 0.5 \cdot 1.84 = 1.42\)
- \(b^{\text{new}} = 0 + 0.5 \cdot 0 = 0\)
New predictions:
- \(p_1^{\text{new}} = \sigma(1.42 \cdot (-2)) = 0.055\)
- \(p_2^{\text{new}} = \sigma(1.42 \cdot (-1)) = 0.195\)
- \(p_3^{\text{new}} = \sigma(1.42 \cdot 1) = 0.805\)
- \(p_4^{\text{new}} = \sigma(1.42 \cdot 2) = 0.945\)
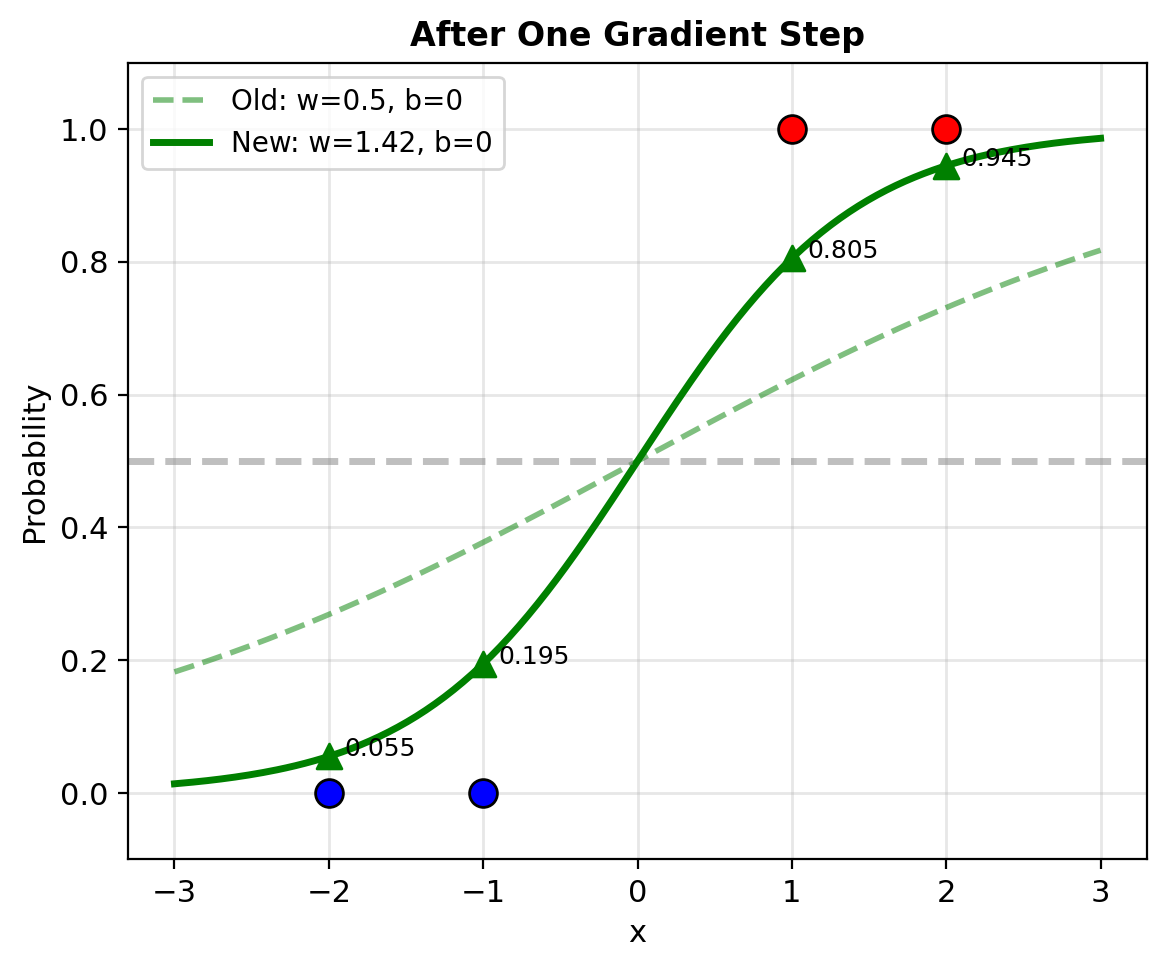
NLL decreased from 1.582 to 0.506
- Class 0 predictions closer to 0
- Class 1 predictions closer to 1
- Better separation between classes
Compute the Hessian (Verify Convexity)
Hessian = matrix of second derivatives
\[\mathbf{H} = \begin{bmatrix} \frac{\partial^2 \ell}{\partial w^2} & \frac{\partial^2 \ell}{\partial w \partial b} \\ \frac{\partial^2 \ell}{\partial b \partial w} & \frac{\partial^2 \ell}{\partial b^2} \end{bmatrix}\]
For logistic regression: \[H_{jk} = -\sum_{i=1}^n p_i(1-p_i) x_{ij} x_{ik}\]
For our 1D example with current \(p = [0.27, 0.38, 0.62, 0.73]\):
Weights: \(p_i(1-p_i)\)
- Point 1: \(0.27(0.73) = 0.197\)
- Point 2: \(0.38(0.62) = 0.236\)
- Point 3: \(0.62(0.38) = 0.236\)
- Point 4: \(0.73(0.27) = 0.197\)
\[H_{ww} = -\sum p_i(1-p_i)x_i^2\] \[= -(0.197 \cdot 4 + 0.236 \cdot 1 + 0.236 \cdot 1 + 0.197 \cdot 4)\] \[= -2.05\]
\[H_{wb} = H_{bw} = -\sum p_i(1-p_i)x_i\] \[= -(0.197 \cdot (-2) + 0.236 \cdot (-1)\] \[\quad + 0.236 \cdot 1 + 0.197 \cdot 2)\] \[= 0\]
\[H_{bb} = -\sum p_i(1-p_i)\] \[= -(0.197 + 0.236 + 0.236 + 0.197)\] \[= -0.866\]
Hessian matrix: \[\mathbf{H} = \begin{bmatrix} -2.05 & 0 \\ 0 & -0.866 \end{bmatrix}\]
For NLL minimization, consider \(-\mathbf{H}\): \[-\mathbf{H} = \begin{bmatrix} 2.05 & 0 \\ 0 & 0.866 \end{bmatrix} \succ 0\]
Positive definite → Convex
Convergence Analysis (Gradient Descent)
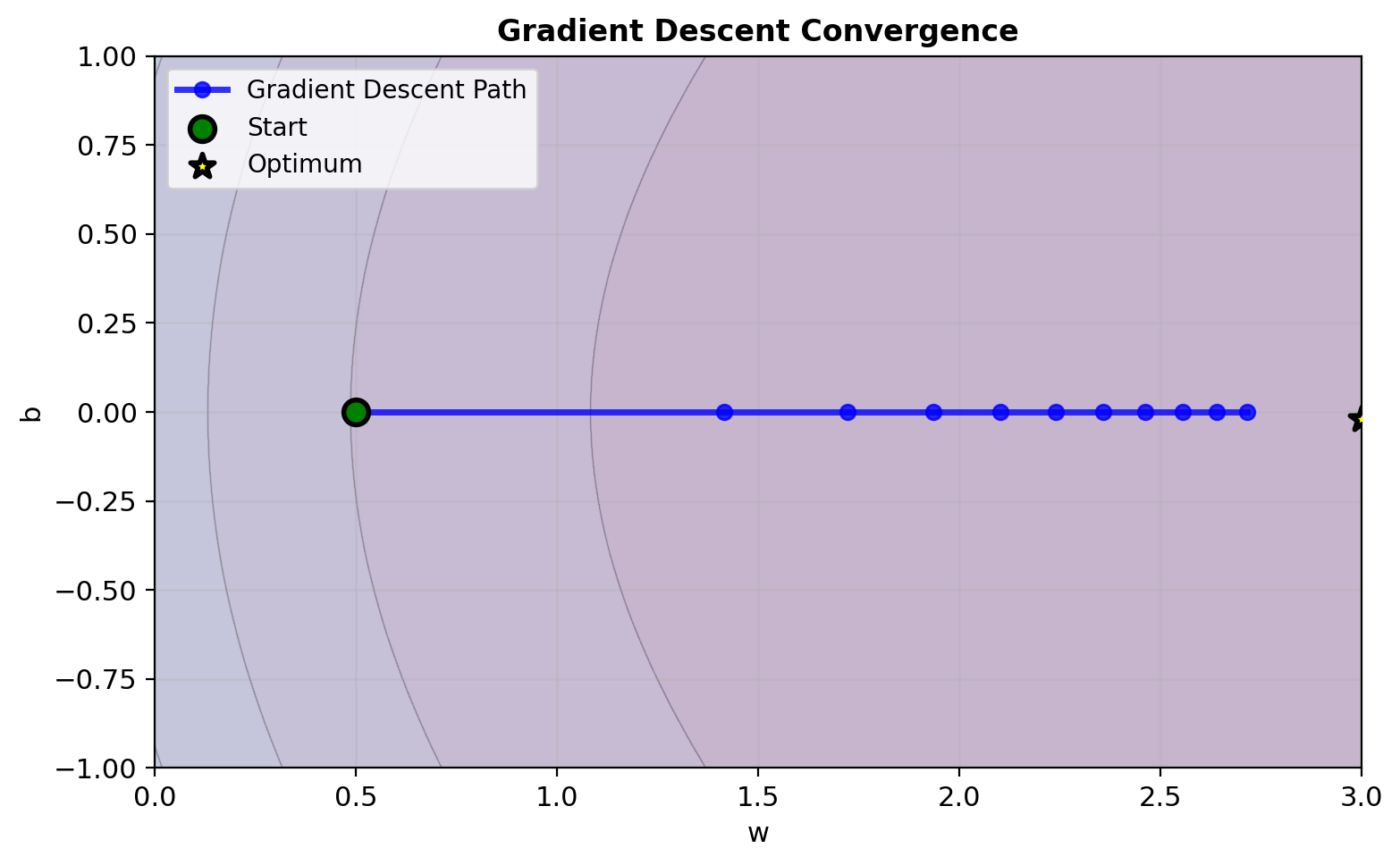
Convexity guarantees convergence to global optimum
Matrix Form for Multiple Features
Generalize to \(n\) samples, \(d\) features:
Data matrix: \(\mathbf{X} \in \mathbb{R}^{n \times d}\) \[\mathbf{X} = \begin{bmatrix} — \mathbf{x}_1^T — \\ — \mathbf{x}_2^T — \\ \vdots \\ — \mathbf{x}_n^T — \end{bmatrix}\]
Predictions: \(\mathbf{p} = \sigma(\mathbf{X}\mathbf{w} + b)\)
Gradient: \[\nabla_\mathbf{w} \ell = \mathbf{X}^T(\mathbf{y} - \mathbf{p})\]
This equals \(\sum_{i=1}^n (y_i - p_i)\mathbf{x}_i\)
Hessian: \[\mathbf{H} = -\mathbf{X}^T\mathbf{D}\mathbf{X}\]
where \(\mathbf{D} = \text{diag}(p_1(1-p_1), \ldots, p_n(1-p_n))\)
Example for our 4-point dataset: \[\mathbf{X} = \begin{bmatrix} -2 \\ -1 \\ 1 \\ 2 \end{bmatrix}, \quad \mathbf{D} = \begin{bmatrix} 0.197 & 0 & 0 & 0 \\ 0 & 0.236 & 0 & 0 \\ 0 & 0 & 0.236 & 0 \\ 0 & 0 & 0 & 0.197 \end{bmatrix}\]
\[\mathbf{H} = -[-2, -1, 1, 2] \mathbf{D} \begin{bmatrix} -2 \\ -1 \\ 1 \\ 2 \end{bmatrix} = -2.05\]
Why Is Logistic Regression Convex?
Theorem: NLL is strictly convex if \(\mathbf{X}\) has full rank.
Proof sketch:
Hessian: \(\mathbf{H} = -\mathbf{X}^T\mathbf{D}\mathbf{X}\)
For any \(\mathbf{v} \neq \mathbf{0}\): \[\mathbf{v}^T(-\mathbf{H})\mathbf{v} = \mathbf{v}^T\mathbf{X}^T\mathbf{D}\mathbf{X}\mathbf{v}\]
Let \(\mathbf{u} = \mathbf{X}\mathbf{v}\): \[= \mathbf{u}^T\mathbf{D}\mathbf{u} = \sum_{i=1}^n p_i(1-p_i)u_i^2\]
Since \(0 < p_i < 1\): all \(p_i(1-p_i) > 0\)
Sum of positive terms → \(\geq 0\)
Equals 0 only if \(\mathbf{u} = \mathbf{0}\)
If \(\mathbf{X}\) full rank: \(\mathbf{X}\mathbf{v} = \mathbf{0} \Rightarrow \mathbf{v} = \mathbf{0}\)
Therefore: \(-\mathbf{H} \succ 0\) (positive definite)
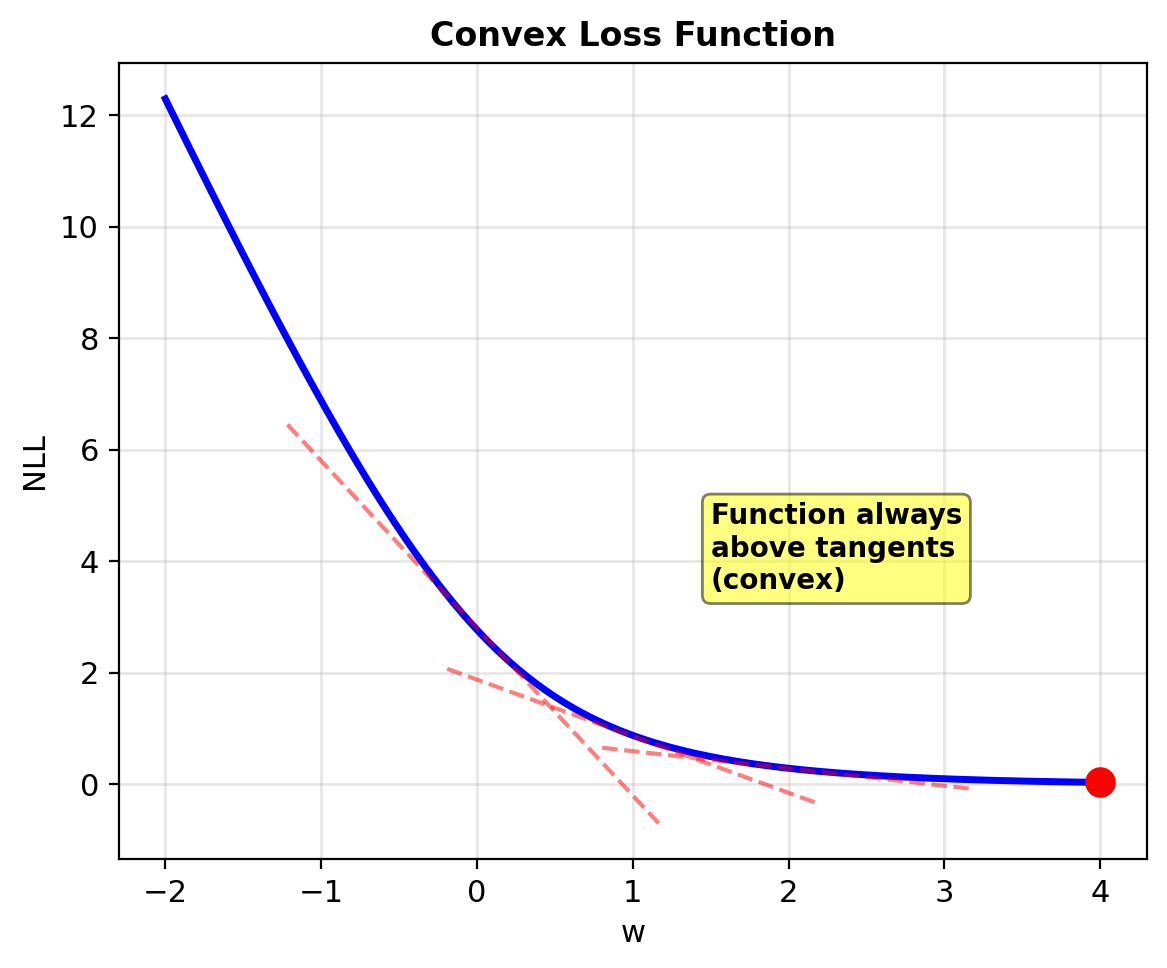
Convexity implications:
| Property | Convex (Logistic) | Non-convex (Neural Net) |
|---|---|---|
| Local minima | None (only global) | Many |
| Optimization | Any method works | Can get stuck |
| Convergence | Guaranteed | No guarantee |
| Initial point | Doesn’t matter | Critical |
| Solution | Unique (if full rank) | Multiple |
Convergence Analysis
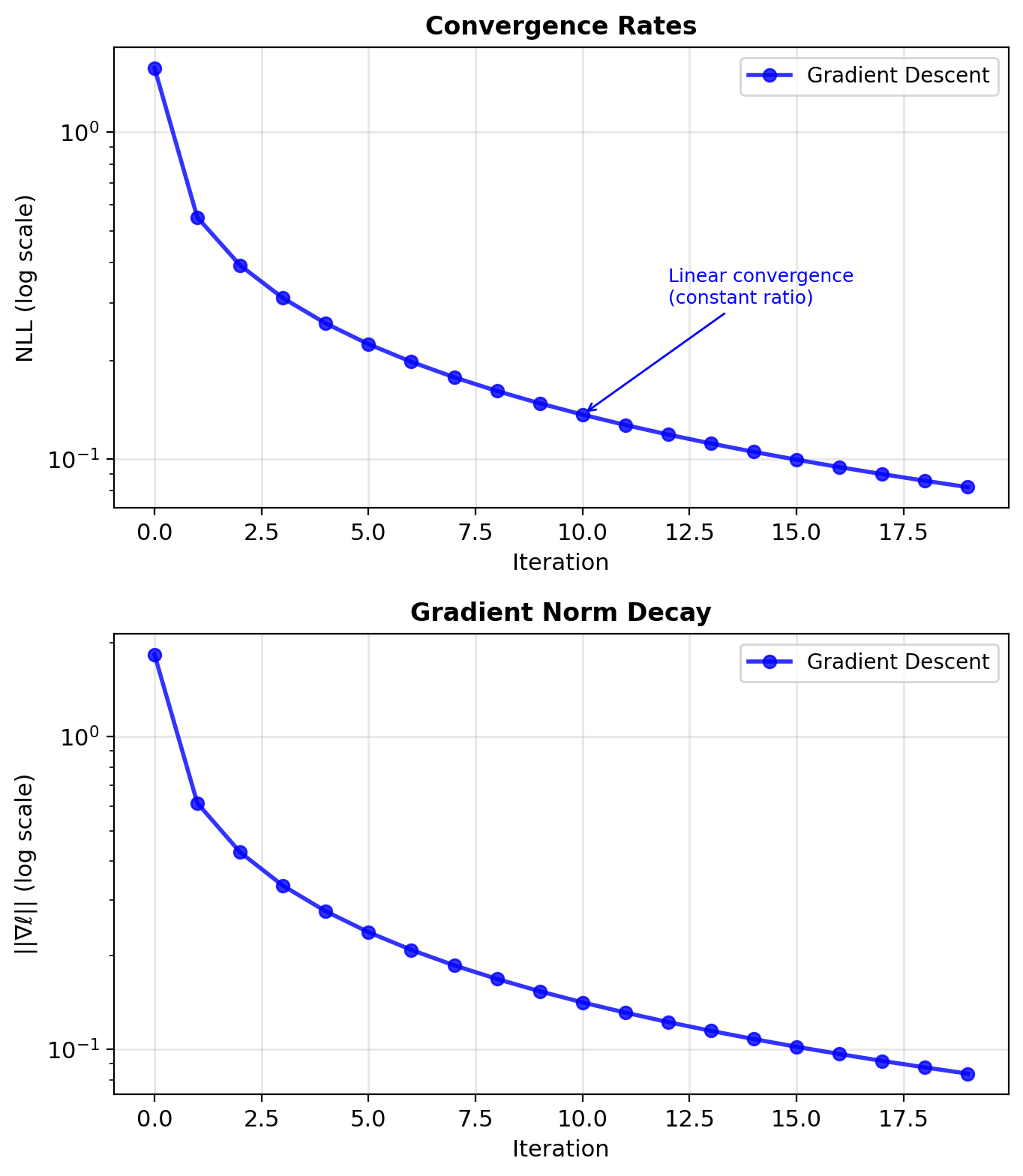
Gradient Descent:
- Linear convergence: \(\epsilon_{t+1} \leq \rho \cdot \epsilon_t\)
- Rate depends on condition number
- Many iterations needed
- Simple, memory efficient
Newton’s Method:
- Quadratic convergence: \(\epsilon_{t+1} \leq c \cdot \epsilon_t^2\)
- Few iterations (5-10 typical)
- Each iteration expensive: \(O(d^3)\)
- Needs to store/invert Hessian
Trade-off:
- Small \(d\) (<1000): Use Newton
- Large \(d\): Use gradient methods
- Very large \(d\): Use stochastic gradient
Fisher Information and Uncertainty
Fisher Information measures parameter certainty: \[\mathcal{I} = \mathbb{E}[-\mathbf{H}] = \mathbb{E}[\mathbf{X}^T\mathbf{D}\mathbf{X}]\]
At convergence for our example:
- \(w^* \approx 2.2\), \(b^* \approx 0\)
- \(p^* = [0.013, 0.050, 0.950, 0.987]\)
Weights at optimum:
- Points 1,4: \(p(1-p) \approx 0.013\) (low)
- Points 2,3: \(p(1-p) \approx 0.048\) (low)
Low weights everywhere → High certainty
Asymptotic distribution: \[\hat{\mathbf{w}} \sim \mathcal{N}(\mathbf{w}^*, \mathcal{I}^{-1}/n)\]
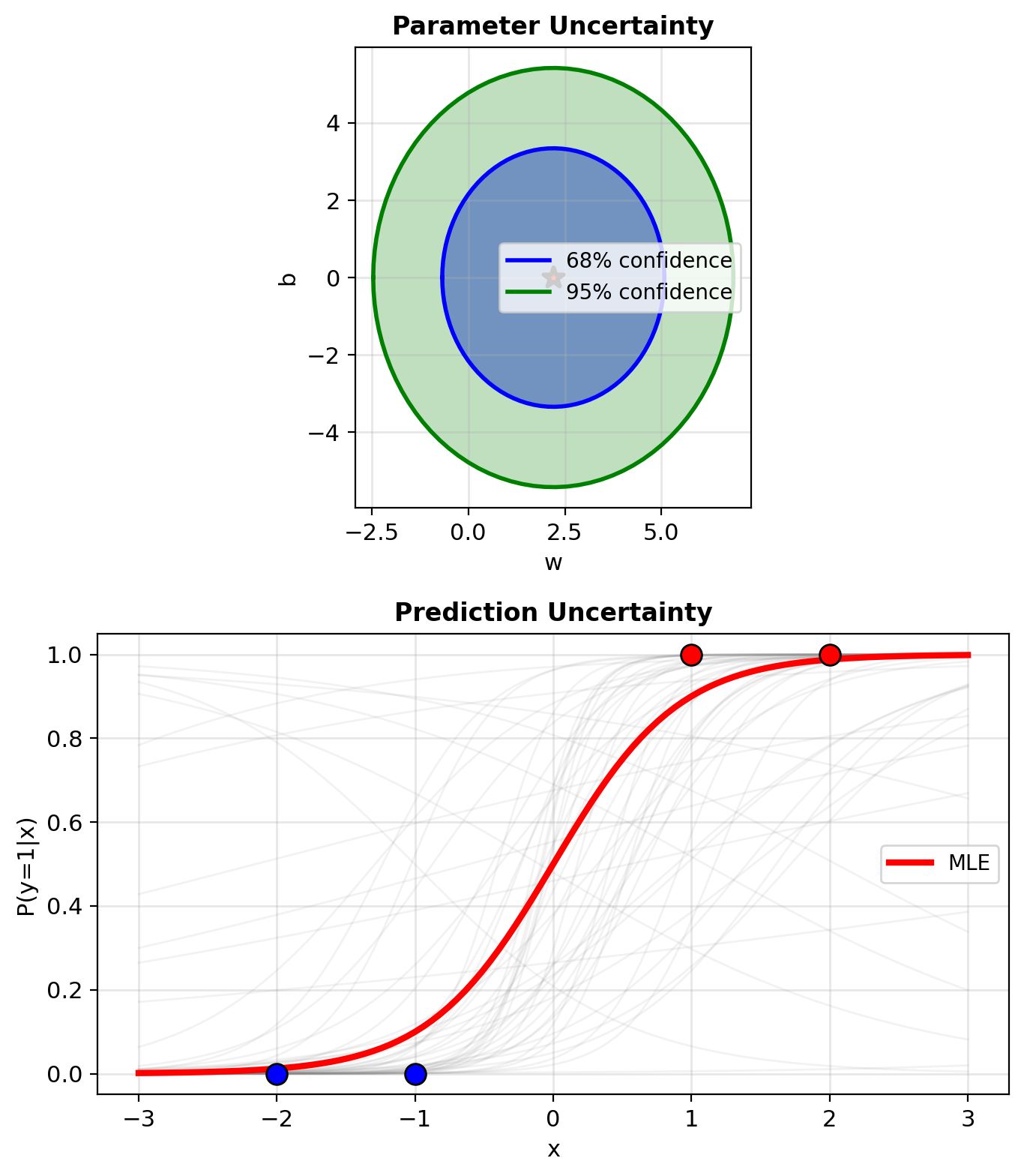
High Fisher information → Low variance → Confident estimates
Multi-Class Classification
From Binary to K > 2 Classes
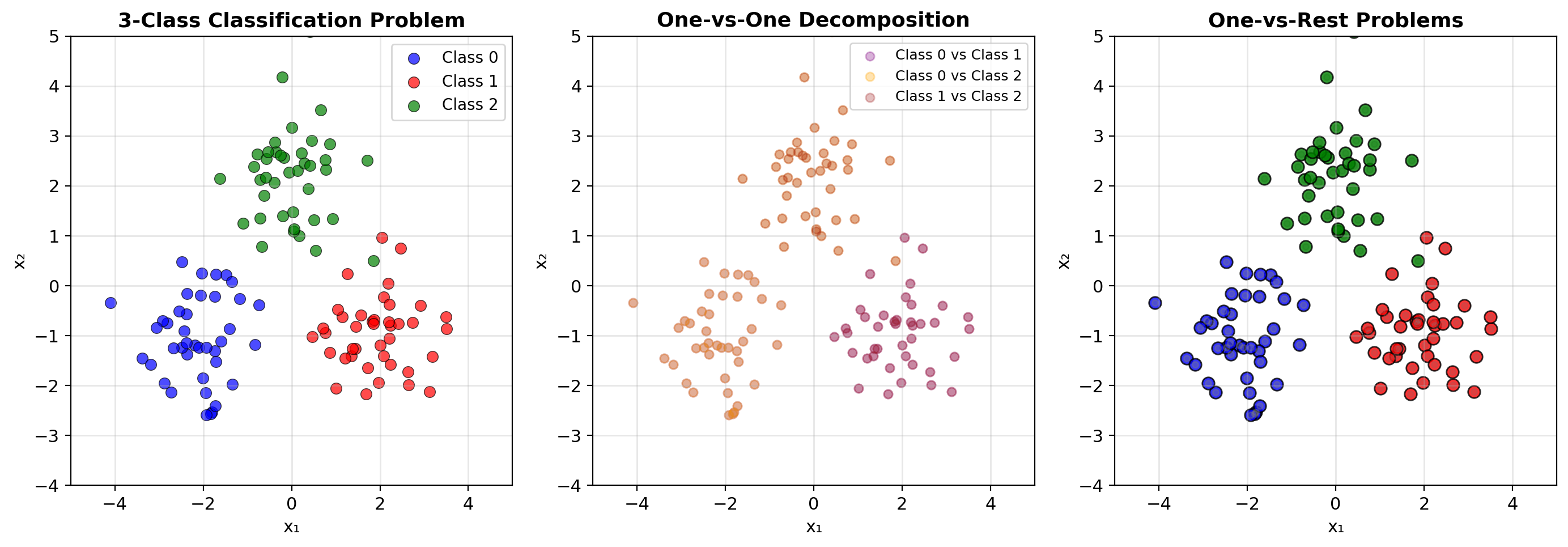
Why One-vs-Rest Fails
One-vs-Rest approach:
- Train K binary classifiers
- Classifier k: class k vs all others
- Predict: argmax of K outputs
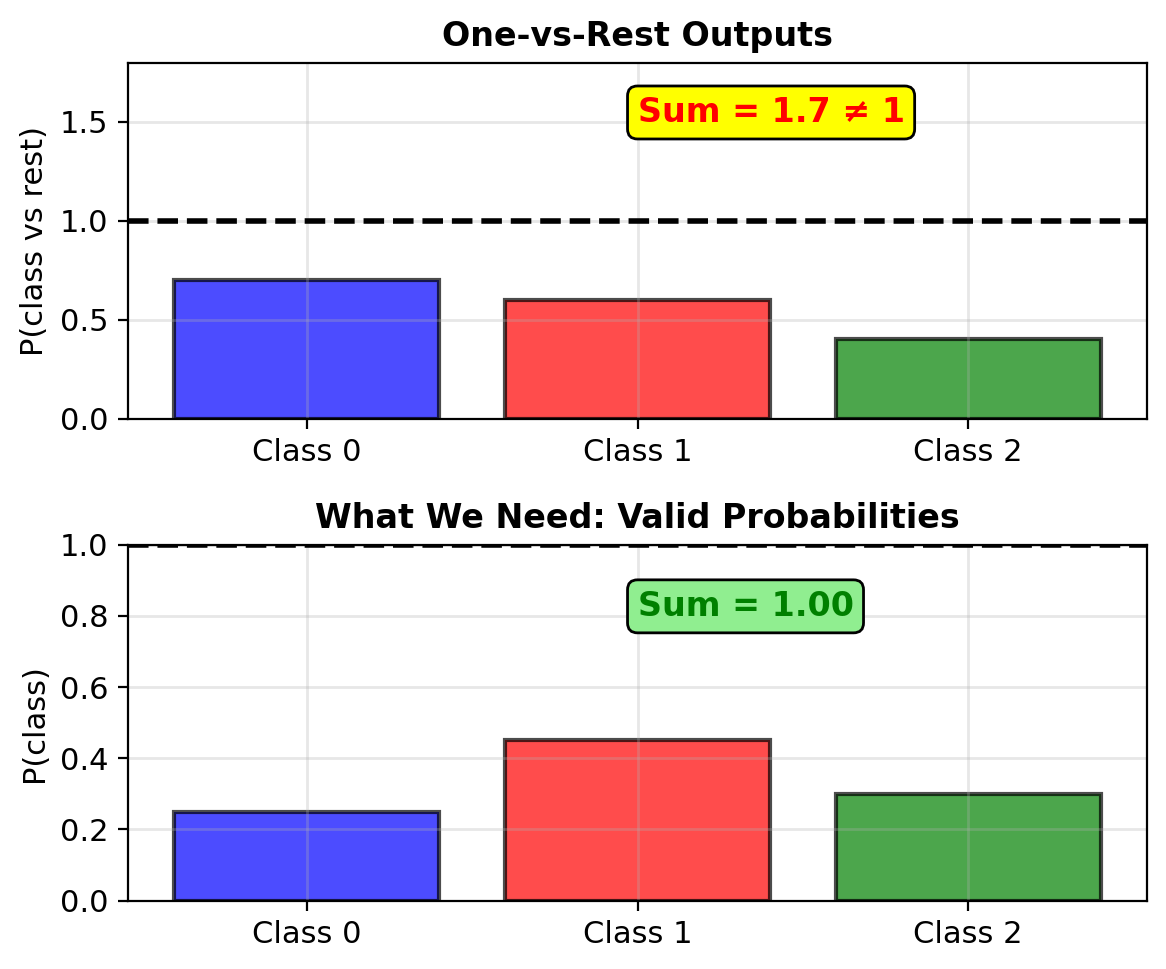
Problem: Probabilities do not sum to 1
Example with 3 classes:
- Classifier 0: P(0 vs rest) = 0.7
- Classifier 1: P(1 vs rest) = 0.6
- Classifier 2: P(2 vs rest) = 0.4
Sum = 1.7 ≠ 1
Not valid probabilities for the K classes
The Softmax Function
Generalize sigmoid to K dimensions:
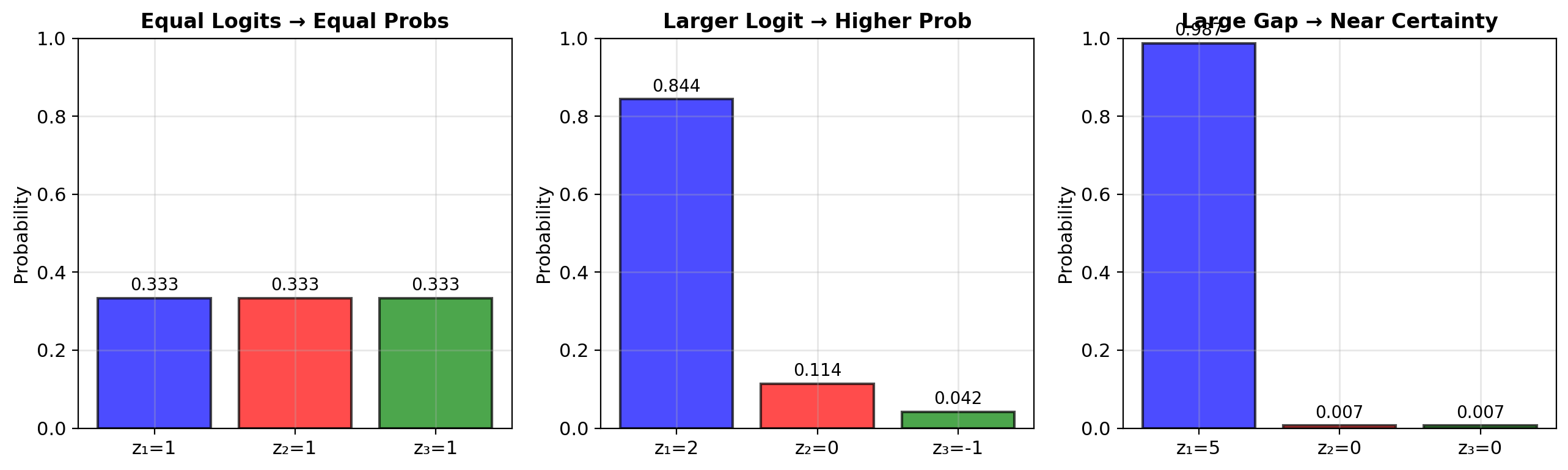
\[\text{softmax}(\mathbf{z})_k = \frac{e^{z_k}}{\sum_{j=1}^K e^{z_j}}\]
For binary case (K=2):
- Let \(z_1 = 0\) (reference class)
- Then: \(p_2 = \frac{e^{z_2}}{e^0 + e^{z_2}} = \frac{1}{1 + e^{-z_2}} = \sigma(z_2)\)
Softmax reduces to sigmoid when K=2
Softmax Properties
Valid probabilities: All outputs in (0,1), sum to 1 \[\sum_{k=1}^K \text{softmax}(\mathbf{z})_k = 1\]
Preserves order: If \(z_i > z_j\), then \(p_i > p_j\)
Translation invariant: \[\text{softmax}(\mathbf{z} + c) = \text{softmax}(\mathbf{z})\]
Since: \(\frac{e^{z_k + c}}{\sum_j e^{z_j + c}} = \frac{e^c \cdot e^{z_k}}{e^c \cdot \sum_j e^{z_j}} = \frac{e^{z_k}}{\sum_j e^{z_j}}\)
Temperature scaling: \[\text{softmax}(\mathbf{z}/T)\]
- \(T \to 0\): approaches argmax (one-hot)
- \(T \to \infty\): uniform distribution

Numerical Stability of Softmax
Problem: Exponentials overflow/underflow
Solution: Take advantage of translation invariance
Subtract maximum before exponent
\[\text{softmax}(\mathbf{z}) = \text{softmax}(\mathbf{z} - \max(\mathbf{z}))\]
z = [1000, 999, 998]
z_stable = z - max(z) = [0, -1, -2]
softmax(z_stable) = [0.665, 0.245, 0.090] # Valid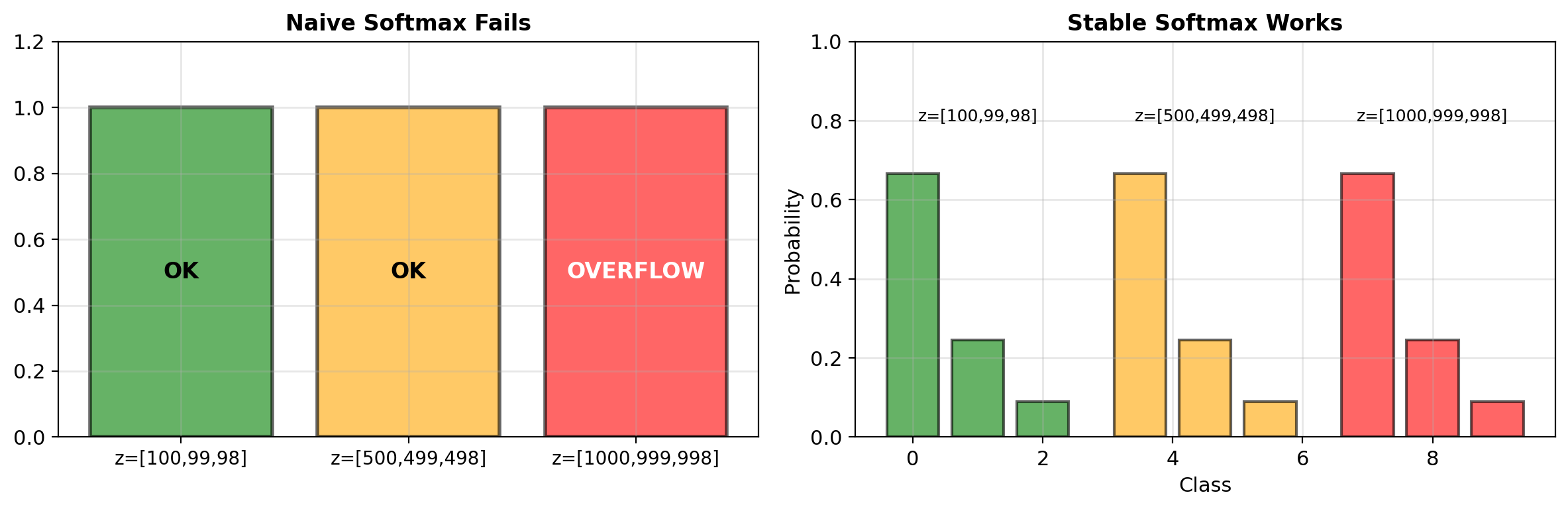
Log-Sum-Exp Trick
Computing log of sum of exponentials:
\[\log\left(\sum_k e^{z_k}\right)\]
Needed for:
- Log-likelihood computation
- Normalizing constant
- Marginalizing over discrete variables
Naive approach fails:
Corrected approach is stable: \[\log\left(\sum_k e^{z_k}\right) = m + \log\left(\sum_k e^{z_k - m}\right)\] where \(m = \max(\mathbf{z})\)
Multinomial Logistic Regression Model
For K classes, we need:
- K linear models: \(z_k = \mathbf{w}_k^T\mathbf{x} + b_k\)
- Parameter matrix: \(\mathbf{W} \in \mathbb{R}^{d \times K}\)
- Bias vector: \(\mathbf{b} \in \mathbb{R}^K\)
Model: \[\mathbf{z} = \mathbf{W}^T\mathbf{x} + \mathbf{b}\] \[P(y=k|\mathbf{x}) = \text{softmax}(\mathbf{z})_k\]
Over-parameterized:
- Can set \(\mathbf{w}_K = \mathbf{0}\), \(b_K = 0\) (reference class)
- Still get valid probabilities
- Reduces parameters by \(d+1\)
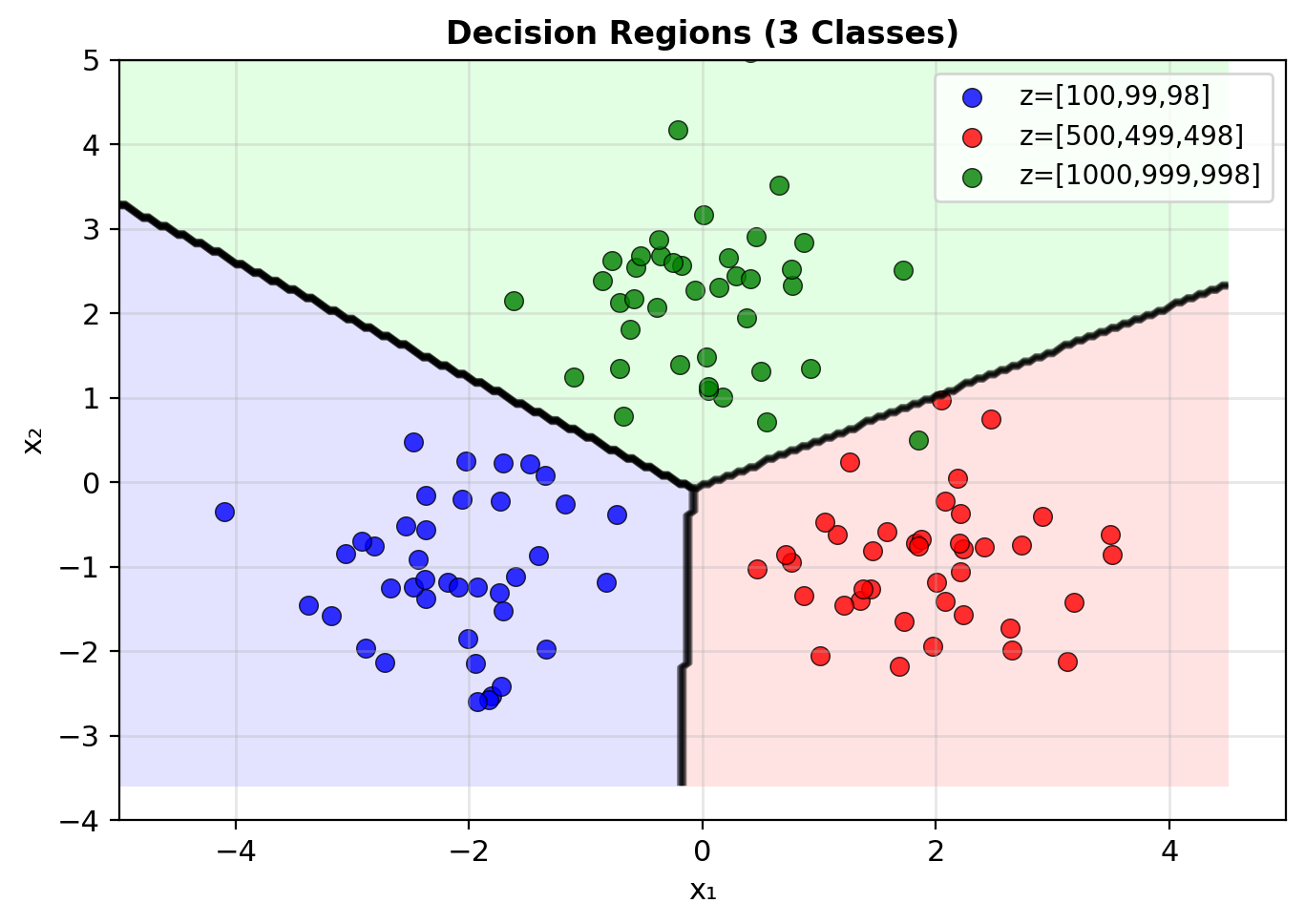
Each boundary is linear (hyperplane)
Cross-Entropy for Multi-Class
One-hot encoding for labels:
- Class 0: \(\mathbf{y} = [1, 0, 0]\)
- Class 1: \(\mathbf{y} = [0, 1, 0]\)
- Class 2: \(\mathbf{y} = [0, 0, 1]\)
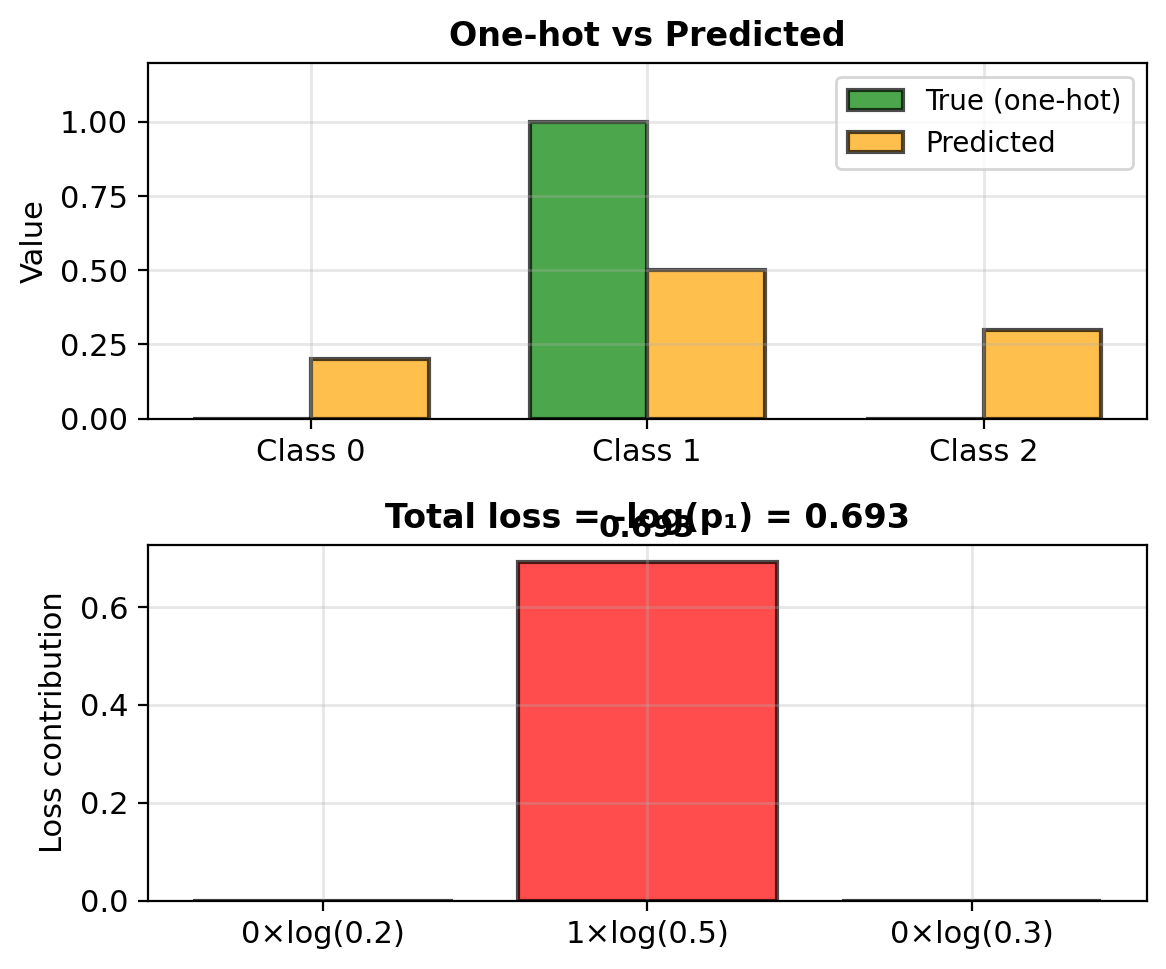
Cross-entropy loss: \[\mathcal{L} = -\sum_{k=1}^K y_k \log p_k\]
Since only one \(y_k = 1\): \[\mathcal{L} = -\log p_{\text{true class}}\]
For entire dataset: \[\text{NLL} = -\sum_{i=1}^n \log p_{i,y_i}\]
where \(p_{i,y_i}\) is predicted probability for true class of sample \(i\)
Gradient for Softmax Cross-Entropy
The gradient has the same form as binary case
For sample \(i\) with true class \(y_i\): \[\frac{\partial \ell_i}{\partial \mathbf{w}_k} = (y_{ik} - p_{ik})\mathbf{x}_i\]
where:
- \(y_{ik} = 1\) if sample \(i\) is class \(k\), else 0
- \(p_{ik} = P(y=k|\mathbf{x}_i)\) from softmax
Derivation sketch:
For loss \(\ell = -\log p_k\) where \(k\) is the true class:
- True class derivative: \(\frac{\partial \ell}{\partial z_k} = -\frac{1}{p_k} \cdot p_k(1-p_k) = -(1-p_k) = p_k - 1\)
- Other classes (\(j \neq k\)): \(\frac{\partial \ell}{\partial z_j} = -\frac{1}{p_k} \cdot (-p_k p_j) = p_j\)
- With one-hot encoding where \(y_k = 1\) (true) or \(y_k = 0\) (other): \[\frac{\partial \ell}{\partial z_k} = p_k - y_k\]
Scalar form: \(\frac{\partial \ell}{\partial z_k} = p_k - y_k\)
Matrix form: \(\nabla_{\mathbf{W}} \ell = \mathbf{X}^T(\mathbf{P} - \mathbf{Y})\)
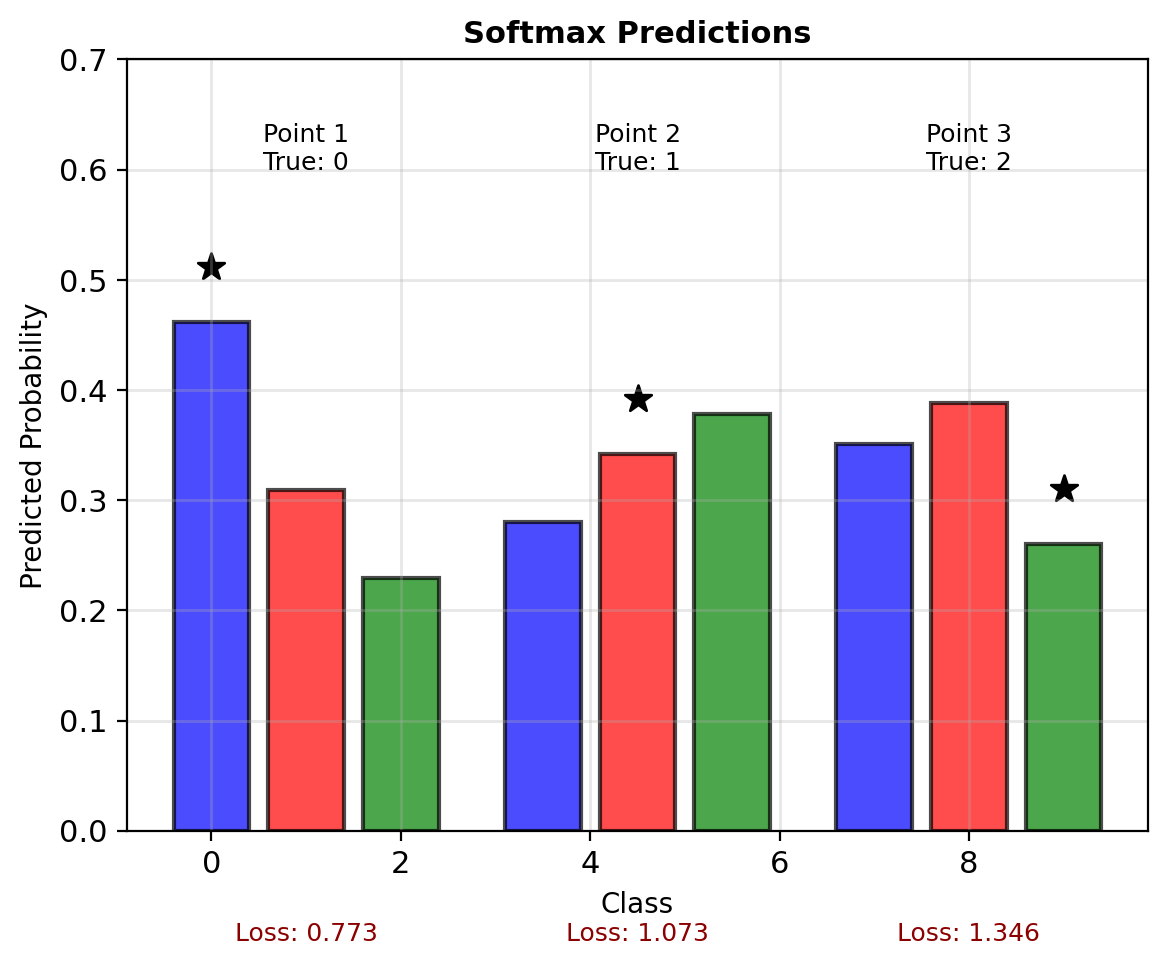
3-Class Softmax Computation
Data: 3 points, 3 classes
Current parameters:
Computing predictions:
Point 1: \(\mathbf{x} = [1, 0]\)
- \(z_0 = 0.5(1) + 0.1(0) + 0.1 = 0.6\)
- \(z_1 = 0.2(1) + 0.3(0) + 0 = 0.2\)
- \(z_2 = 0(1) + 0(0) - 0.1 = -0.1\)
- \(\mathbf{p} = \text{softmax}([0.6, 0.2, -0.1]) = [0.47, 0.32, 0.21]\)
- True class: 0, Loss: \(-\log(0.47) = 0.76\)
Softmax Derivative (Jacobian)
The softmax has vector input and vector output, so its derivative is a Jacobian matrix:
3×3 Example with \(\mathbf{p} = [0.5, 0.3, 0.2]\):
\[\mathbf{J} = \begin{bmatrix} \frac{\partial p_1}{\partial z_1} & \frac{\partial p_1}{\partial z_2} & \frac{\partial p_1}{\partial z_3} \\ \frac{\partial p_2}{\partial z_1} & \frac{\partial p_2}{\partial z_2} & \frac{\partial p_2}{\partial z_3} \\ \frac{\partial p_3}{\partial z_1} & \frac{\partial p_3}{\partial z_2} & \frac{\partial p_3}{\partial z_3} \end{bmatrix}\]
General formula: \[\frac{\partial p_i}{\partial z_j} = \begin{cases} p_i(1 - p_i) & \text{if } i = j \\ -p_i p_j & \text{if } i \neq j \end{cases}\]
For this example: \[\mathbf{J} = \begin{bmatrix} 0.5(1-0.5) & -0.5(0.3) & -0.5(0.2) \\ -0.3(0.5) & 0.3(1-0.3) & -0.3(0.2) \\ -0.2(0.5) & -0.2(0.3) & 0.2(1-0.2) \end{bmatrix} = \begin{bmatrix} 0.25 & -0.15 & -0.10 \\ -0.15 & 0.21 & -0.06 \\ -0.10 & -0.06 & 0.16 \end{bmatrix}\]
Rows sum to 0 (probabilities sum to 1)
Binary to Multiclass
Regularization
Separable Data Leads to Weight Explosion in MLE
Perfect separation scenario:
# 2D data with polynomial features
X = [[-2, -1], [-1, -2], [1, 2], [2, 1]]
y = [0, 0, 1, 1]
# Add polynomial features
X_poly = [[x1, x2, x1², x2², x1x2]
for x1, x2 in X]With 5 features for 4 points:
- Can achieve perfect separation
- MLE drives weights → ∞
- Predictions become 0 or 1 exactly
- No unique solution
The problem:
- Loss keeps decreasing: NLL → 0
- But weights explode: ||w|| → ∞
- Model becomes overconfident
- Poor generalization to new data
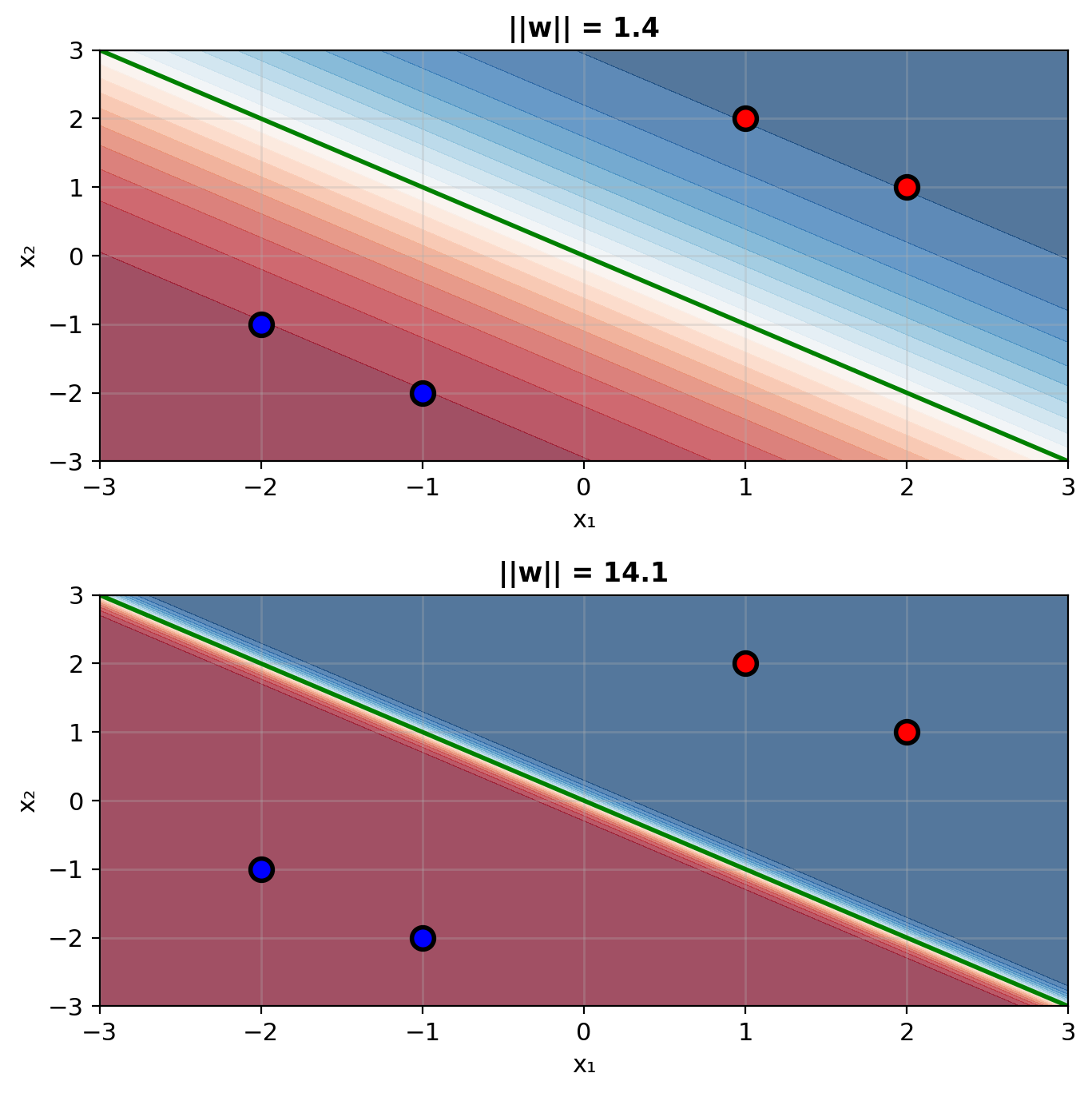
As ||w|| increases:
- Decision boundary sharpens
- Probabilities → 0 or 1
- Model becomes “too sure”
Weight Explosion in High Dimensions
Example: 100 features, 80 samples
Without regularization:
n, d = 80, 100 # More features than samples
X = np.random.randn(n, d)
y = (X @ w_true + noise > 0).astype(int)What happens during optimization:
- Early iterations: Reasonable weights
- Middle: Some weights grow large
- Late: Many weights explode
- “Solution”: Perfect training accuracy
- But: Poor generalization (test performance)
Weight explosion occurs when:
- \(d > n\) (more features than samples)
- Features are highly correlated
- Perfect or near-perfect separation exists

Loss decreases but weights are unstable.
L2 Regularization (Ridge regression)
Modified objective: \[\mathcal{L}_{\text{ridge}} = \underbrace{-\ell(\mathbf{w})}_{\text{NLL}} + \underbrace{\lambda ||\mathbf{w}||^2}_{\text{penalty}}\]
Gradient with regularization: \[\nabla \mathcal{L}_{\text{ridge}} = -\mathbf{X}^T(\mathbf{y} - \mathbf{p}) + 2\lambda\mathbf{w}\]
Compare to unregularized: \[\nabla \ell = \mathbf{X}^T(\mathbf{y} - \mathbf{p})\]
Effect: Pull weights toward zero
Update rule: \[\mathbf{w} \leftarrow \mathbf{w} - \eta[\nabla \ell - 2\lambda\mathbf{w}]\] \[= (1 - 2\eta\lambda)\mathbf{w} - \eta\nabla \ell\]
Weight decay: Shrink by factor \((1 - 2\eta\lambda)\)
L2 Regularization = Bias toward smaller weights.
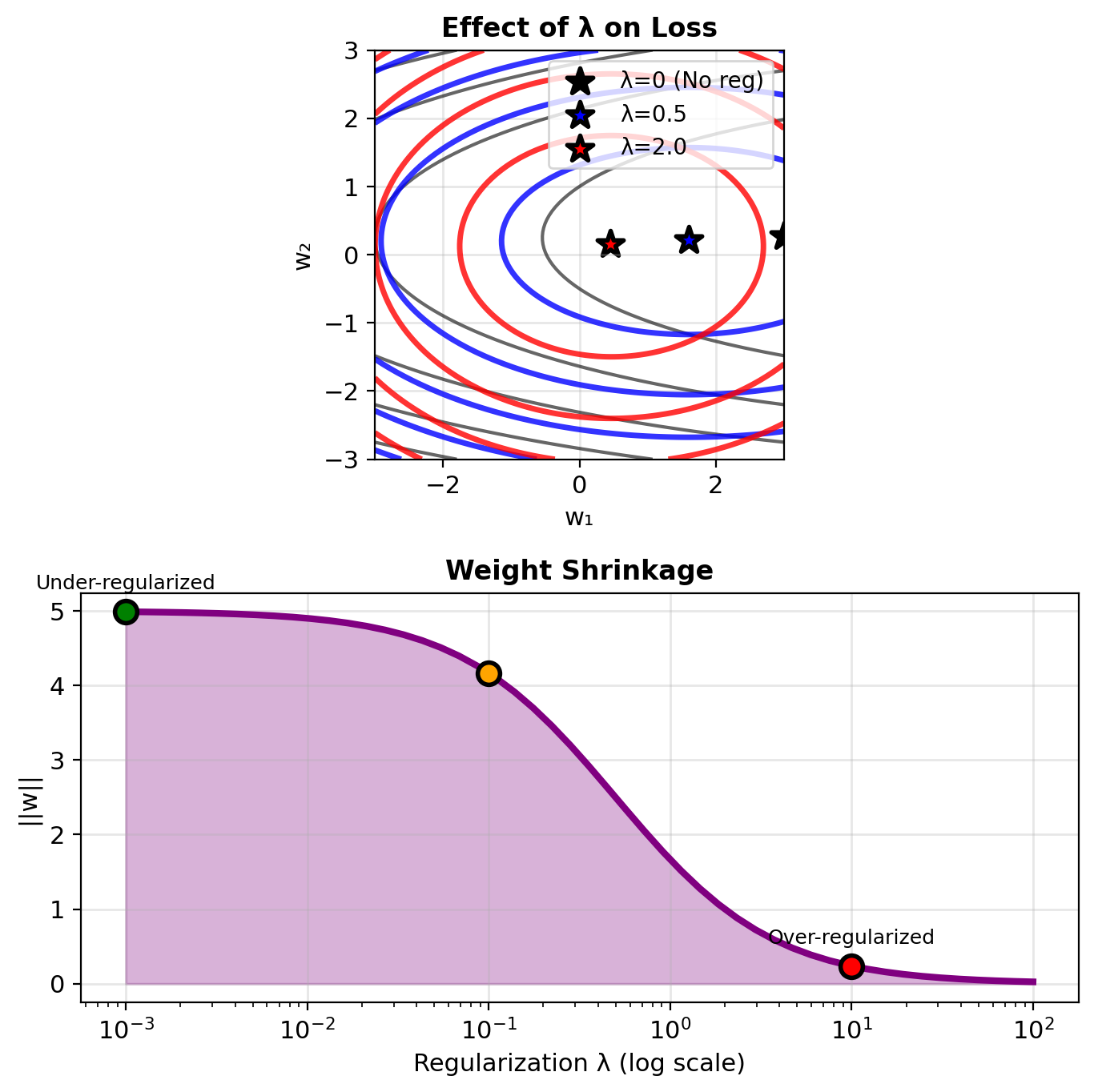
Larger λ → Smaller weights → More stable model
Bayesian Interpretation
L2 regularization = Gaussian prior
Prior on weights: \[P(\mathbf{w}) = \mathcal{N}(\mathbf{0}, \sigma^2\mathbf{I})\] \[\propto \exp\left(-\frac{||\mathbf{w}||^2}{2\sigma^2}\right)\]
MAP estimation: \[\hat{\mathbf{w}}_{\text{MAP}} = \arg\max_\mathbf{w} P(\mathcal{D}|\mathbf{w})P(\mathbf{w})\]
Taking logarithm: \[= \arg\max_\mathbf{w} \left[\log P(\mathcal{D}|\mathbf{w}) + \log P(\mathbf{w})\right]\] \[= \arg\max_\mathbf{w} \left[\ell(\mathbf{w}) - \frac{||\mathbf{w}||^2}{2\sigma^2}\right]\]
With \(\lambda = \frac{1}{2\sigma^2}\): \[= \arg\min_\mathbf{w} \left[-\ell(\mathbf{w}) + \lambda ||\mathbf{w}||^2\right]\]
This is Ridge regression
Smaller σ gives stronger regularization

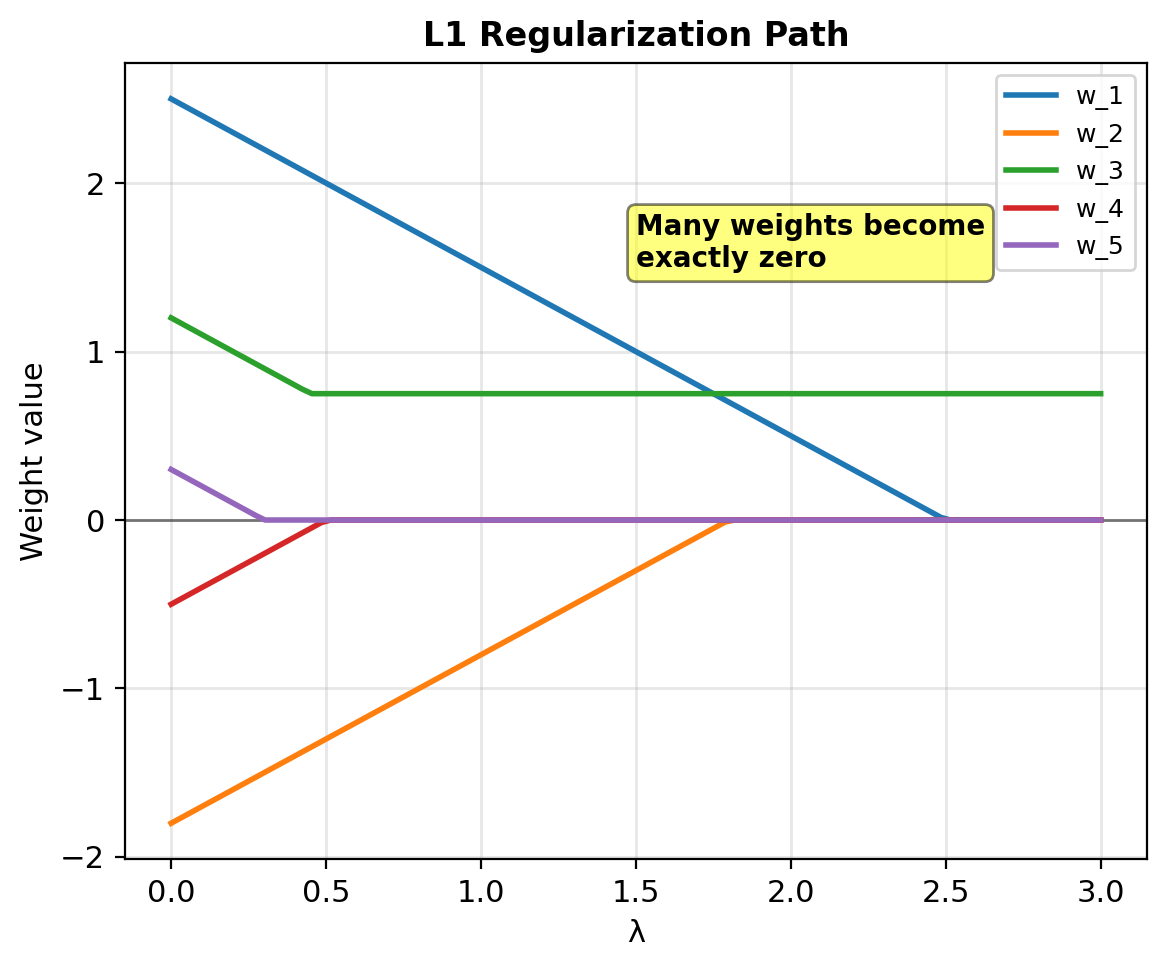
L1 Regularization (LASSO)
LASSO (Least Absolute Shrinkage and Selection Operator)
L1 penalty: \[\mathcal{L}_{\text{lasso}} = -\ell(\mathbf{w}) + \lambda ||\mathbf{w}||_1\] \[= -\ell(\mathbf{w}) + \lambda \sum_{j=1}^d |w_j|\]
Subgradient (not differentiable at 0): \[\partial_{w_j} \mathcal{L} = -\frac{\partial \ell}{\partial w_j} + \lambda \cdot \text{sign}(w_j)\]
where \(\text{sign}(w) = \begin{cases} +1 & w > 0 \\ [-1, 1] & w = 0 \\ -1 & w < 0 \end{cases}\)
Induces exact sparsity: Many weights become exactly zero
Bayesian view: Laplace prior \[P(\mathbf{w}) \propto \exp(-\lambda ||\mathbf{w}||_1)\]
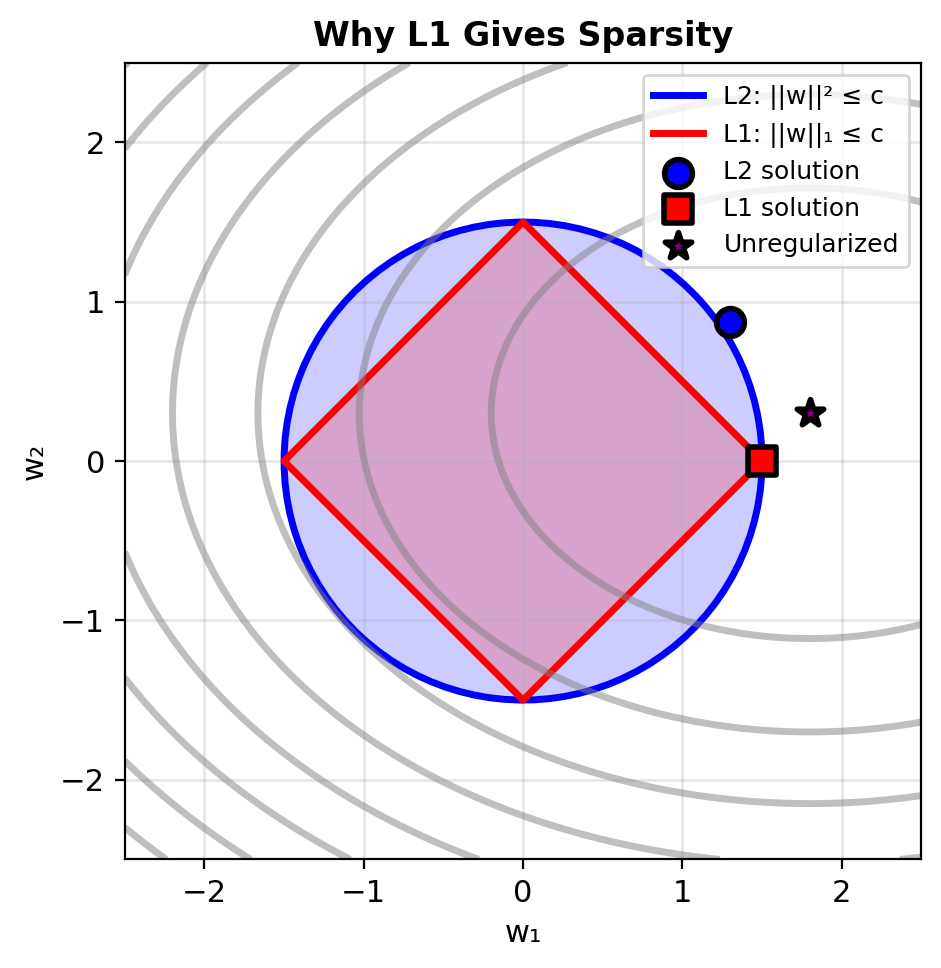
L1 hits corners → Some weights exactly 0
Elastic Net: Combined L1 and L2
Combine L1 and L2: \[\mathcal{L}_{\text{elastic}} = -\ell(\mathbf{w}) + \lambda_1 ||\mathbf{w}||_1 + \lambda_2 ||\mathbf{w}||^2\]
Alternative parameterization: \[= -\ell(\mathbf{w}) + \lambda\left[\alpha ||\mathbf{w}||_1 + \frac{1-\alpha}{2}||\mathbf{w}||^2\right]\]
where:
- \(\alpha = 1\): Pure L1 (Lasso)
- \(\alpha = 0\): Pure L2 (Ridge)
- \(0 < \alpha < 1\): Mix of both
Advantages:
- Sparsity from L1
- Grouping from L2 (correlated features)
- Stability when \(p > n\)
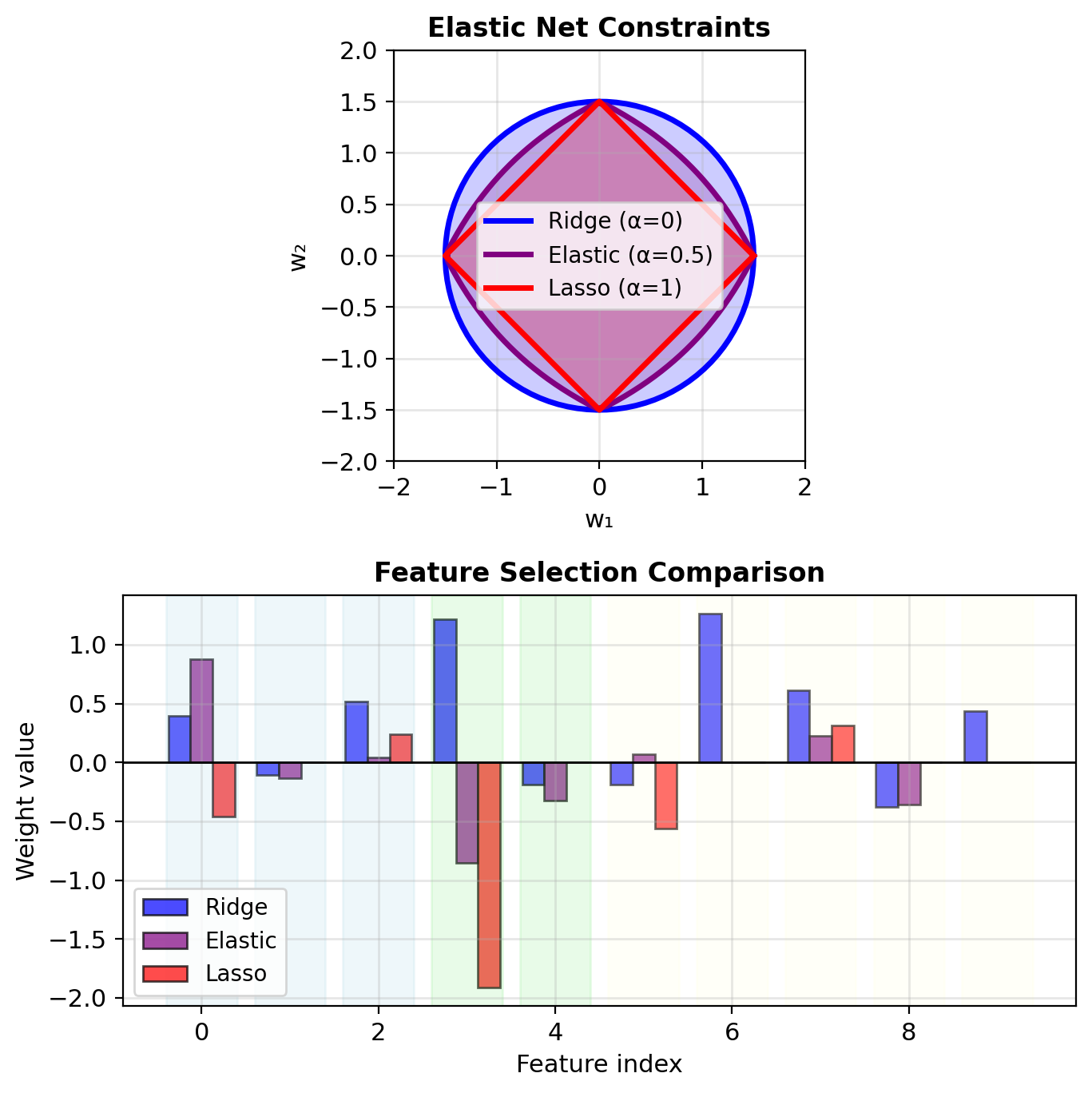
Elastic Net: Selects groups of correlated features
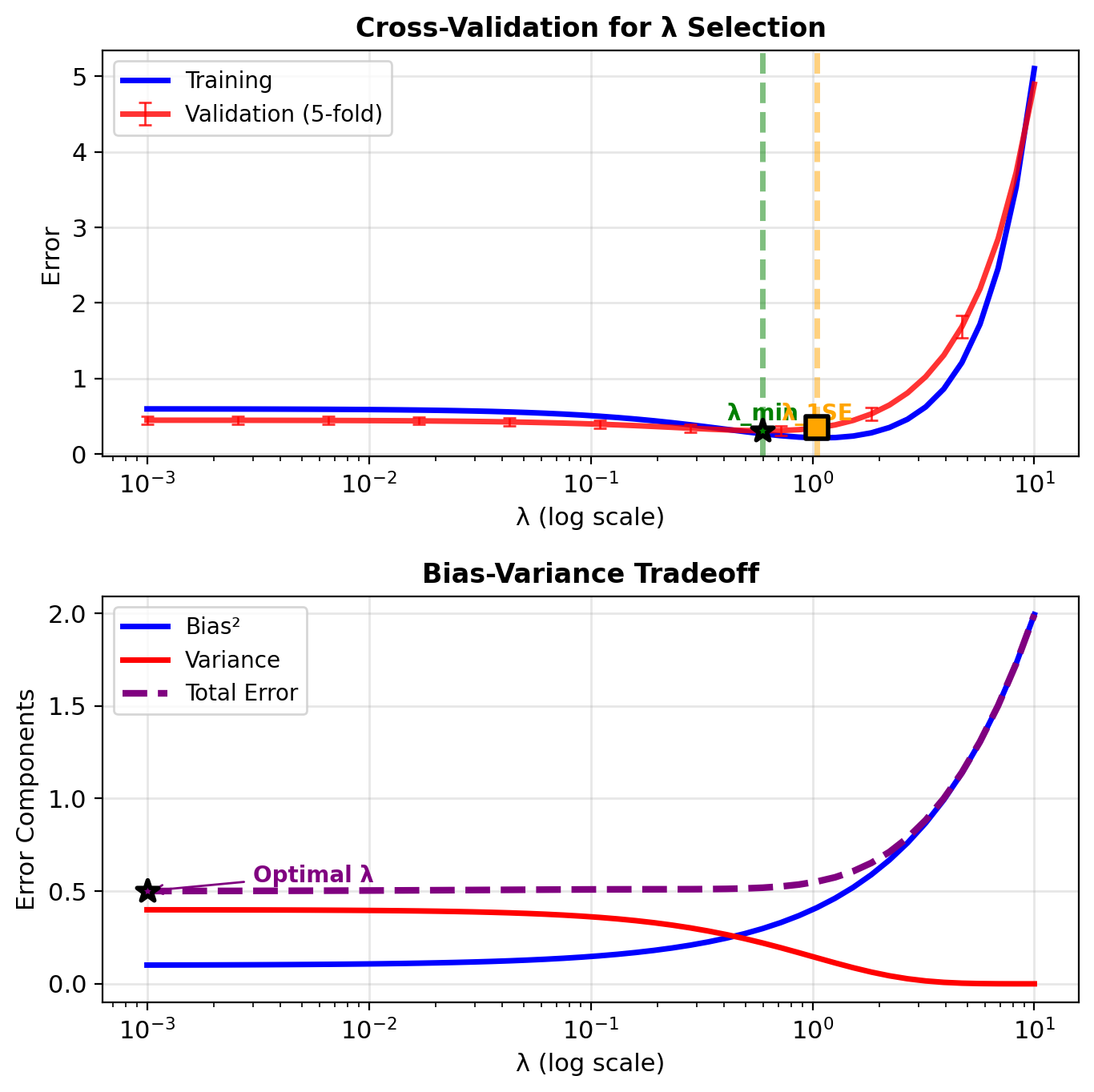
Cross-Validation for λ
k-fold cross-validation:
Split data into \(k\) “folds”
For each \(\lambda\):
- Train on \(k-1\) folds
- Validate on remaining fold
- Repeat \(k\) times
Average validation error
Choose \(\lambda\) with lowest error
Common choices:
- \(k = 5\) or \(k = 10\)
- Leave-one-out: \(k = n\) (expensive)
One standard error rule:
- Find \(\lambda_{\text{min}}\) with minimum validation error
- Find largest \(\lambda\) within 1 standard error of minimum
- Choose simpler model (larger \(\lambda\)) when comparable
Larger λ within 1 SE yields simpler models with comparable performance
Ridge Implementation
import numpy as np
from scipy.special import expit as sigmoid
def logistic_regression_l2(X, y, lambda_reg=0.1, lr=0.01, max_iter=1000):
"""Logistic regression with L2 regularization."""
n, d = X.shape
w = np.zeros(d)
b = 0
losses = []
for iteration in range(max_iter):
# Forward pass
z = X @ w + b
p = sigmoid(z)
# Loss = NLL + penalty
nll = -np.mean(y * np.log(p + 1e-10) + (1-y) * np.log(1-p + 1e-10))
penalty = lambda_reg * np.sum(w**2)
loss = nll + penalty
losses.append(loss)
# Gradients with regularization
grad_w = -X.T @ (y - p) / n + 2 * lambda_reg * w
grad_b = -np.mean(y - p)
# Update parameters
w -= lr * grad_w
b -= lr * grad_b
if iteration % 200 == 0:
print(f"Iter {iteration}: Loss = {loss:.4f}, ||w|| = {np.linalg.norm(w):.4f}")
return w, b, losses
# Generate synthetic data
np.random.seed(42)
n, d = 100, 10
X = np.random.randn(n, d)
w_true = np.random.randn(d) * 2
y = (X @ w_true + 0.5 * np.random.randn(n) > 0).astype(float)
# Compare different λ values
for lambda_val in [0, 0.1, 1.0]:
print(f"\nλ = {lambda_val}:")
w, b, losses = logistic_regression_l2(
X, y, lambda_reg=lambda_val, lr=0.1, max_iter=400
)
print(f"Final ||w|| = {np.linalg.norm(w):.3f}")
λ = 0:
Iter 0: Loss = 0.6931, ||w|| = 0.0390
Iter 200: Loss = 0.2209, ||w|| = 2.6773
Final ||w|| = 3.670
λ = 0.1:
Iter 0: Loss = 0.6931, ||w|| = 0.0390
Iter 200: Loss = 0.5105, ||w|| = 0.9713
Final ||w|| = 0.972
λ = 1.0:
Iter 0: Loss = 0.6931, ||w|| = 0.0390
Iter 200: Loss = 0.6575, ||w|| = 0.1738
Final ||w|| = 0.174Logistic Regression to Neural Networks
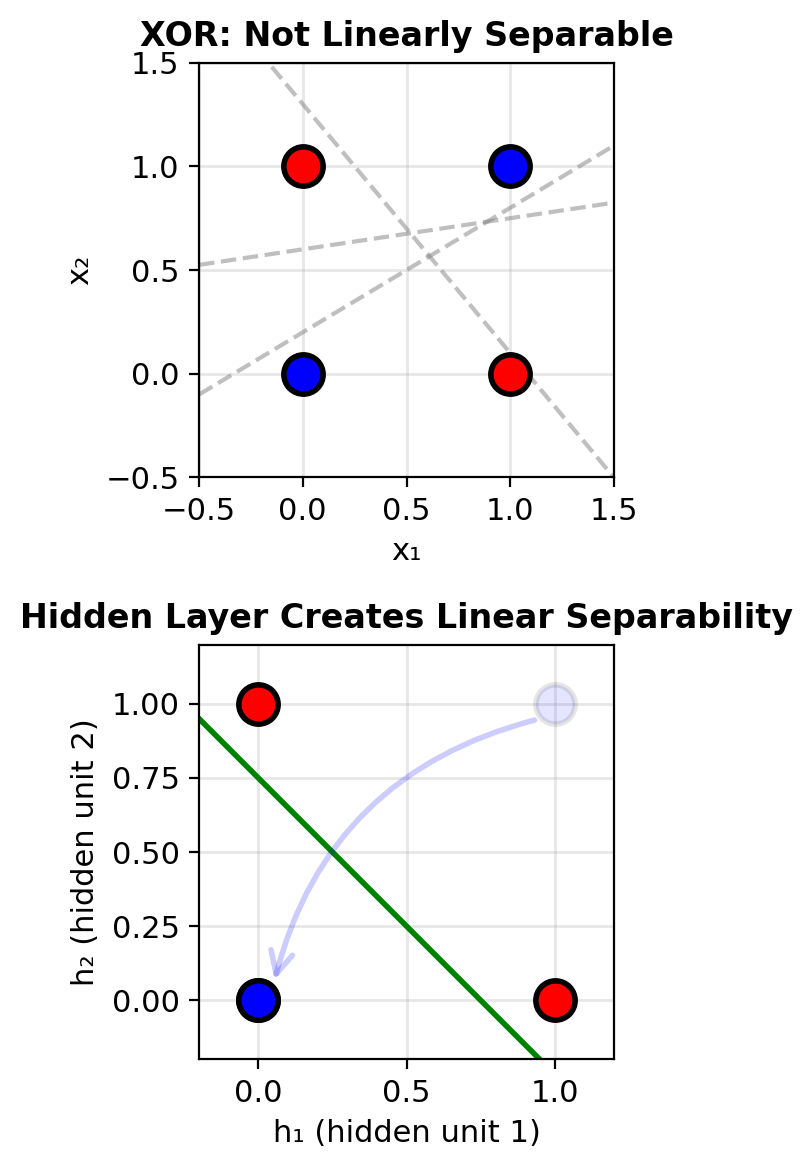
The “XOR Problem”
XOR (Exclusive OR):
- (0,0) → Class 0 (blue)
- (0,1) → Class 1 (red)
- (1,0) → Class 1 (red)
- (1,1) → Class 0 (blue)
No linear boundary exists
Any line through the space:
- Misclassifies at least 2 points
- 50% accuracy at best
Logistic regression fails because: \[P(y=1|\mathbf{x}) = \sigma(\mathbf{w}^T\mathbf{x} + b)\] enforces linear decision boundary
Solution: Add hidden layer
- Transform features nonlinearly
- Create linearly separable representation
- 2 hidden units sufficient for XOR
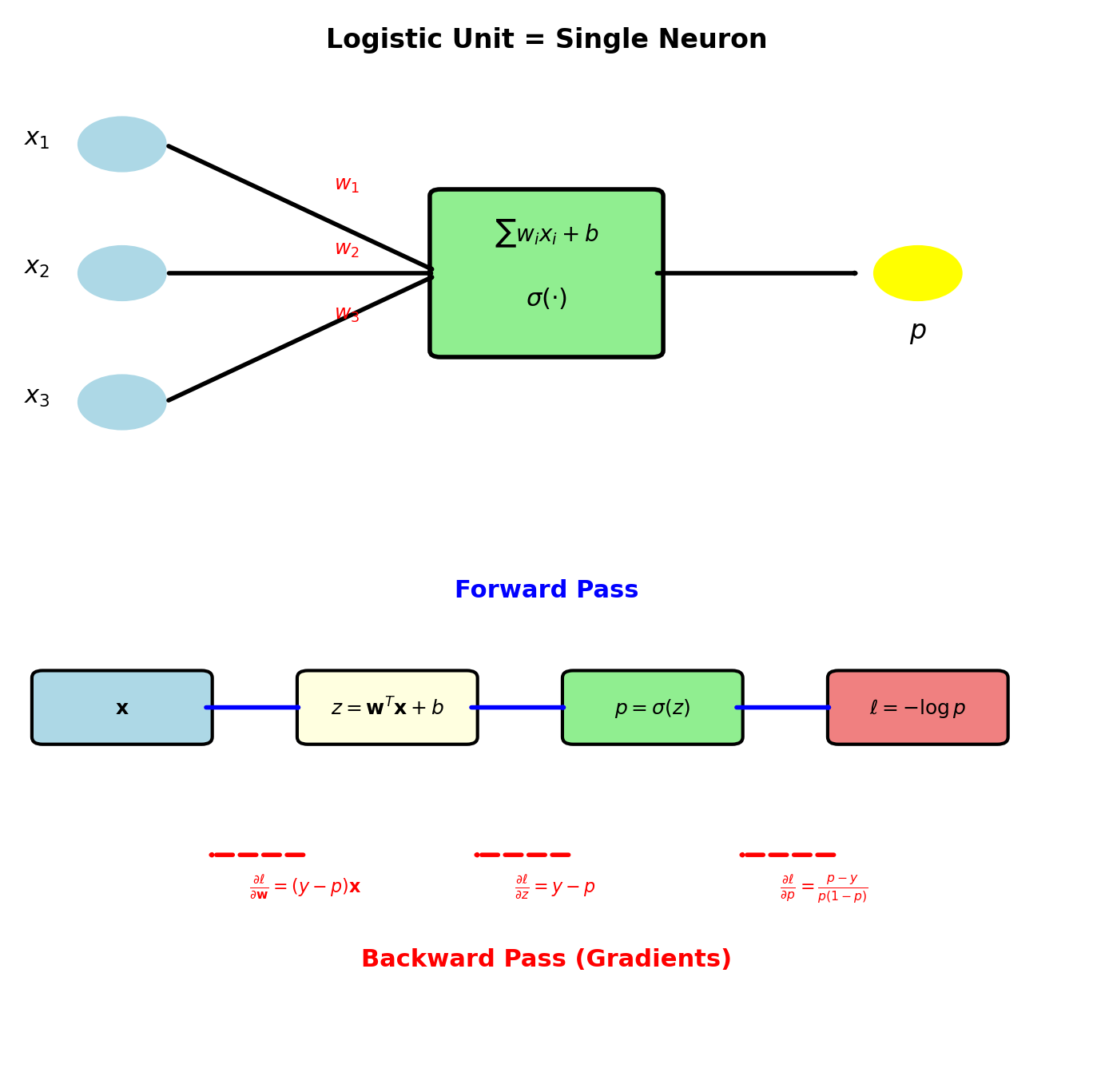
Logistic Regression Is a Single Neuron
Equivalence:
\[z = \mathbf{w}^T\mathbf{x} + b\] \[p = \sigma(z) = \frac{1}{1 + e^{-z}}\]
- Inputs: \(\mathbf{x} \in \mathbb{R}^d\)
- Weights: \(\mathbf{w} \in \mathbb{R}^d\)
- Bias: \(b \in \mathbb{R}\)
- Activation: sigmoid \(\sigma(\cdot)\)
- Output: \(p \in (0, 1)\)
Neural network building blocks, neurons
Forward pass: \[\mathbf{x} \to \mathbf{w}^T\mathbf{x} + b \to \sigma(\cdot) \to p\]
Backward pass (gradient): \[\frac{\partial \ell}{\partial \mathbf{w}} = (y - p)\mathbf{x}\]
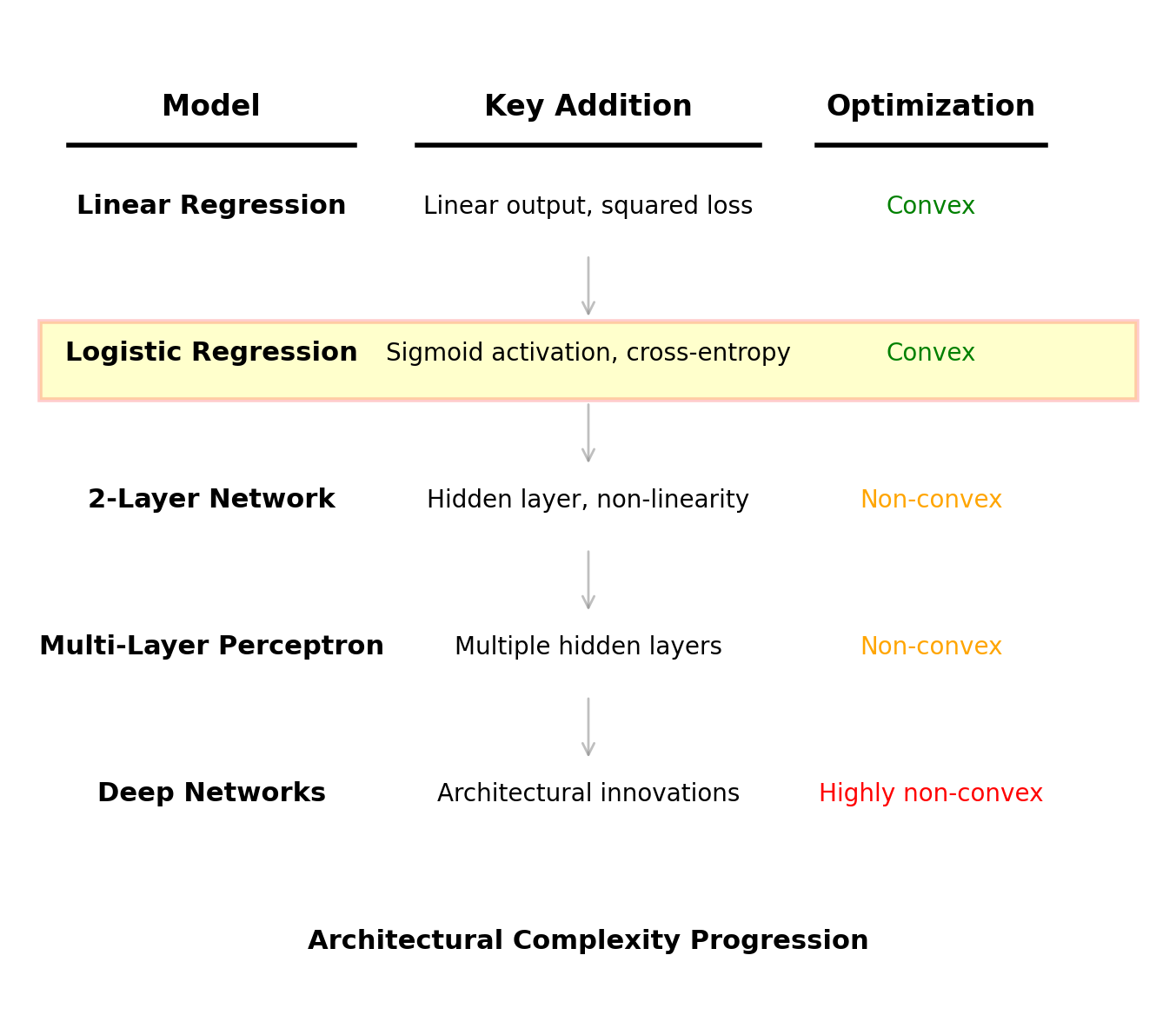
Neural Networks Stack Logistic Units
Two-layer network: \[\mathbf{h} = \sigma(\mathbf{W}_1\mathbf{x} + \mathbf{b}_1)\] \[p = \sigma(\mathbf{w}_2^T\mathbf{h} + b_2)\]
where:
- \(\mathbf{W}_1 \in \mathbb{R}^{m \times d}\): First layer weights
- \(\mathbf{h} \in \mathbb{R}^m\): Hidden layer (m neurons)
- \(\mathbf{w}_2 \in \mathbb{R}^m\): Output layer weights
Consequences:
- Non-convex optimization: multiple local minima
- Universal approximation: arbitrary function fitting
- Hidden layers: learned representations
- Backpropagation: chain rule through layers
Same cross-entropy loss: \[\min_{\mathbf{W}_1, \mathbf{W}_2} -\sum_{i=1}^n [y_i \log p_i + (1-y_i)\log(1-p_i)]\]
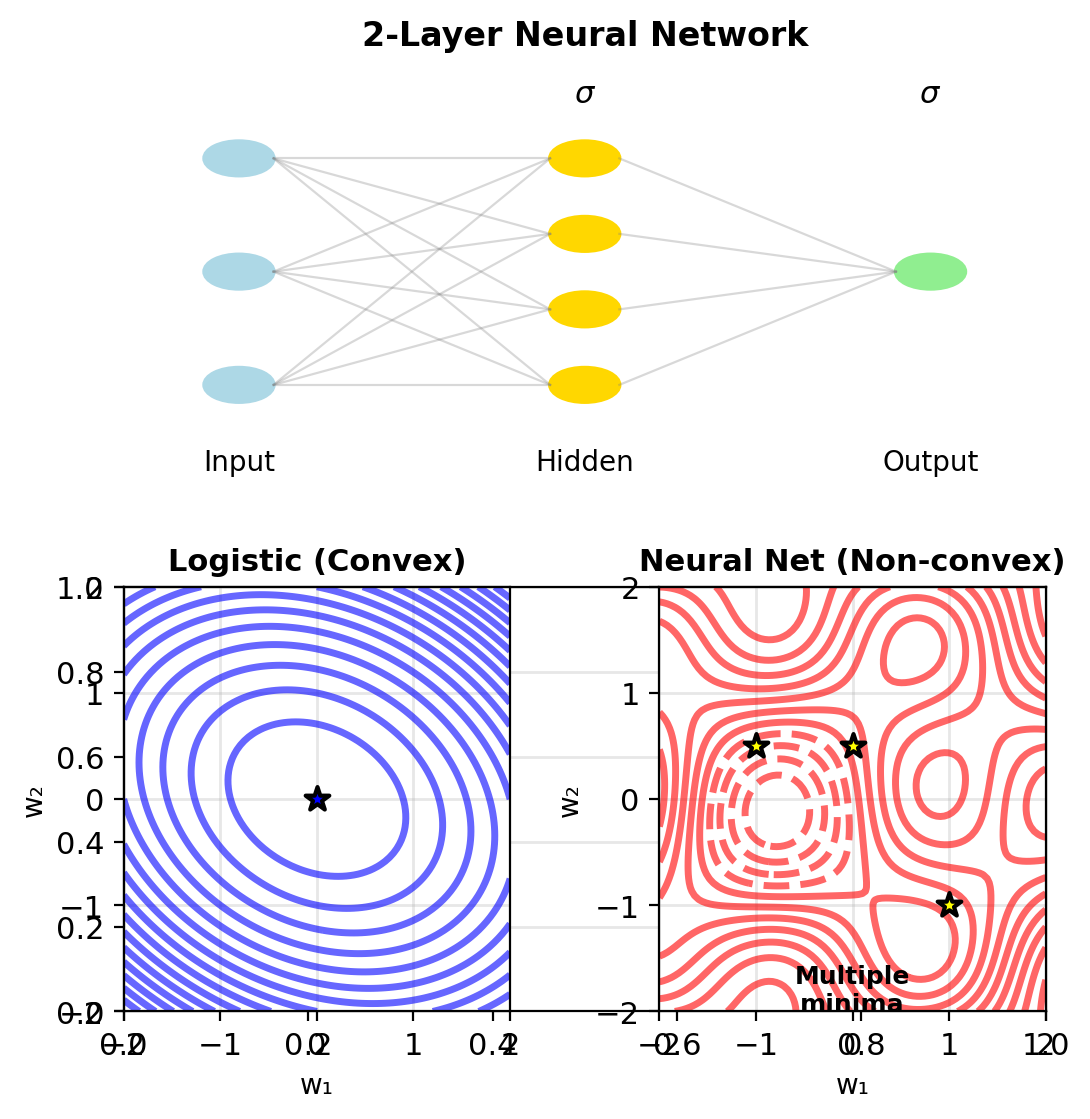
“Deep” Neural Network = Compose Multiple Logistic Units
Logistic regression = single-layer neural network
Single neuron with sigmoid activation:
- Input: \(\mathbf{x} \in \mathbb{R}^d\)
- Weights: \(\mathbf{w} \in \mathbb{R}^d\), bias \(b\)
- Output: \(\sigma(\mathbf{w}^T\mathbf{x} + b)\)
Gradient computation: \[\nabla_\mathbf{w} \mathcal{L} = \mathbf{X}^T(\mathbf{p} - \mathbf{y})\]
Gradient formula extends to:
- Softmax (multiple outputs)
- Hidden layers (chain rule)
- Deep networks (backpropagation)