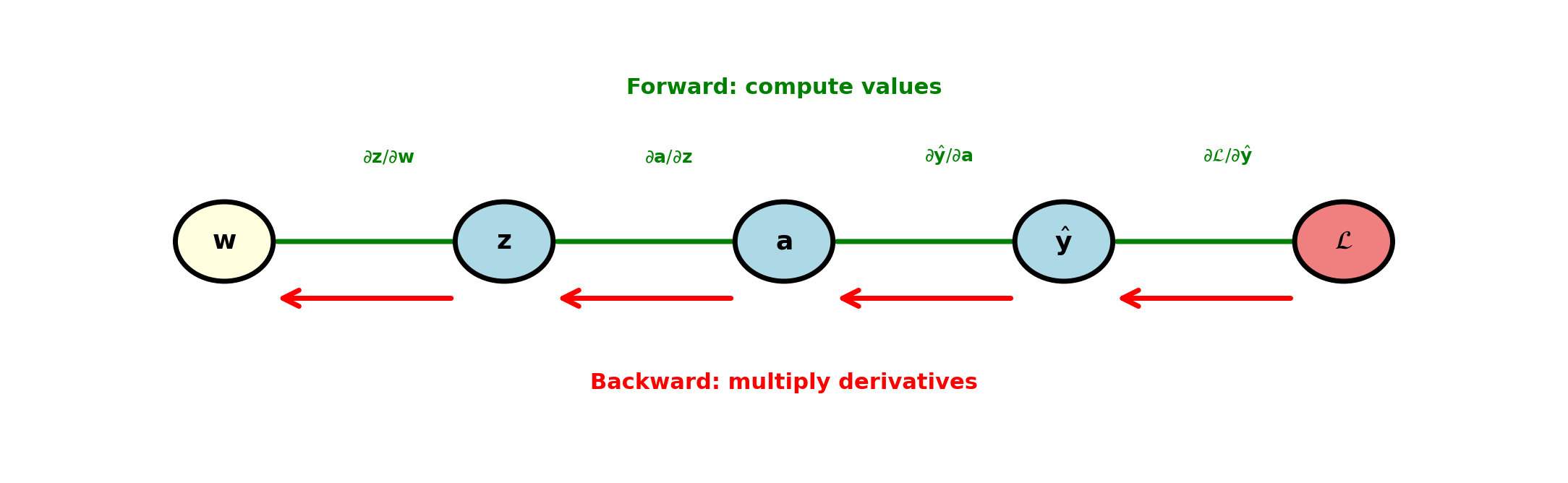
Backpropagation
EE 541 - Unit 6
Fall 2025
Outline
Foundations
- Composition challenge
- Chain rule foundation
- Delta method: \(\delta^{(l)} = \frac{\partial \mathcal{L}}{\partial s^{(l)}}\)
- Gradient accumulation
- Recursion: \(\boldsymbol{\delta}^{(l)} = (W^{(l+1)})^T \boldsymbol{\delta}^{(l+1)} \odot \sigma'(\mathbf{s}^{(l)})\)
- Weight gradient as outer product
Algorithm & Implementation
- Forward, backward, gradients
- Complexity: backward ≈ 2× forward
- Local gradient principle
- Modular composition
- Gradient verification
- Detecting bugs
- Vanishing gradients
From Single Layer to Deep Networks
Training Neural Networks Requires Gradients
Single variable: \(y = f(g(x))\): \[\frac{dy}{dx} = \frac{df}{dg} \cdot \frac{dg}{dx}\]
“Deep” composition: \(y = f(g(h(x)))\): \[\frac{dy}{dx} = \frac{df}{dg} \cdot \frac{dg}{dh} \cdot \frac{dh}{dx}\]
Backpropagation applies chain rule systematically: Each layer computes local derivative. Composition handled by passing gradients backward.
Deep network with \(L\) layers: \(\frac{\partial \mathcal{L}}{\partial \mathbf{w}^{(1)}}\) requires \(L\) chain rule applications. Direct computation: 1 forward pass + 1 backward pass.
Logistic Regression Gradient
Model: \(p = \sigma(z)\) where \(z = \mathbf{w}^T\mathbf{x} + b\)
Sigmoid: \(\sigma(z) = \frac{1}{1 + e^{-z}}\)
Loss (binary cross-entropy): \[\mathcal{L} = -[y\log p + (1-y)\log(1-p)]\]
Derivative of sigmoid: \[\begin{align} \sigma'(z) &= \frac{d}{dz}\left(\frac{1}{1+e^{-z}}\right)\\ &= \frac{e^{-z}}{(1+e^{-z})^2}\\ &= \frac{1}{1+e^{-z}} \cdot \frac{e^{-z}}{1+e^{-z}}\\ &= \sigma(z)(1-\sigma(z)) \end{align}\]
Loss gradient w.r.t. \(z\): \[\begin{align} \frac{\partial \mathcal{L}}{\partial z} &= \frac{\partial \mathcal{L}}{\partial p} \cdot \frac{\partial p}{\partial z}\\ &= \left[-\frac{y}{p} + \frac{1-y}{1-p}\right] \cdot \sigma'(z)\\ &= \left[-\frac{y}{p} + \frac{1-y}{1-p}\right] \cdot p(1-p)\\ &= -(y - p) \end{align}\]
Weight gradient: \[\frac{\partial \mathcal{L}}{\partial \mathbf{w}} = \frac{\partial \mathcal{L}}{\partial z} \cdot \frac{\partial z}{\partial \mathbf{w}} = (p - y)\mathbf{x}\]
Bias gradient: \[\frac{\partial \mathcal{L}}{\partial b} = \frac{\partial \mathcal{L}}{\partial z} \cdot \frac{\partial z}{\partial b} = p - y\]
Example: Numerical Verification
Setup:
- Input: \(\mathbf{x} = [2, 1]^T\)
- Weights: \(\mathbf{w} = [0.5, -0.3]^T\)
- Bias: \(b = 0\)
- Label: \(y = 1\)
Forward pass:
\[z = \mathbf{w}^T\mathbf{x} + b = \begin{bmatrix} 0.5 & -0.3 \end{bmatrix} \begin{bmatrix} 2 \\ 1 \end{bmatrix} + 0 = 0.7\]
\[p = \sigma(0.7) = \frac{1}{1+e^{-0.7}} = 0.668\]
Loss: \[\begin{align} \mathcal{L} &= -[y\log p + (1-y)\log(1-p)] = -[1 \cdot \log(0.668) + 0 \cdot \log(0.332)]\\ &= -\log(0.668) = 0.404 \end{align}\]
Gradient computation:
\[\frac{\partial \mathcal{L}}{\partial z} = p - y = 0.668 - 1 = -0.332\]
\[\frac{\partial \mathcal{L}}{\partial \mathbf{w}} = \frac{\partial \mathcal{L}}{\partial z} \mathbf{x} = -0.332 \begin{bmatrix} 2 \\ 1 \end{bmatrix} = \begin{bmatrix} -0.664 \\ -0.332 \end{bmatrix}\]
\[\frac{\partial \mathcal{L}}{\partial b} = \frac{\partial \mathcal{L}}{\partial z} = -0.332\]
Numerical check (finite difference with \(\epsilon = 10^{-5}\)):
For \(w_1\): \[\frac{\mathcal{L}(w_1 + \epsilon) - \mathcal{L}(w_1 - \epsilon)}{2\epsilon} = -0.664\]
Matches analytical gradient
Composition in Deep Networks
Two-layer network:
\[\mathbf{x} \xrightarrow{W^{(1)}} \mathbf{z}^{(1)} \xrightarrow{\sigma} \mathbf{a}^{(1)} \xrightarrow{W^{(2)}} \mathbf{z}^{(2)} \xrightarrow{\sigma} \hat{y}\]
Forward pass equations:
Layer 1: \[\mathbf{z}^{(1)} = W^{(1)}\mathbf{x} + \mathbf{b}^{(1)}\] \[\mathbf{a}^{(1)} = \sigma(\mathbf{z}^{(1)})\]
Layer 2: \[\mathbf{z}^{(2)} = W^{(2)}\mathbf{a}^{(1)} + \mathbf{b}^{(2)}\] \[\hat{y} = \sigma(\mathbf{z}^{(2)})\]
Loss: \[\mathcal{L} = -[y\log \hat{y} + (1-y)\log(1-\hat{y})]\]
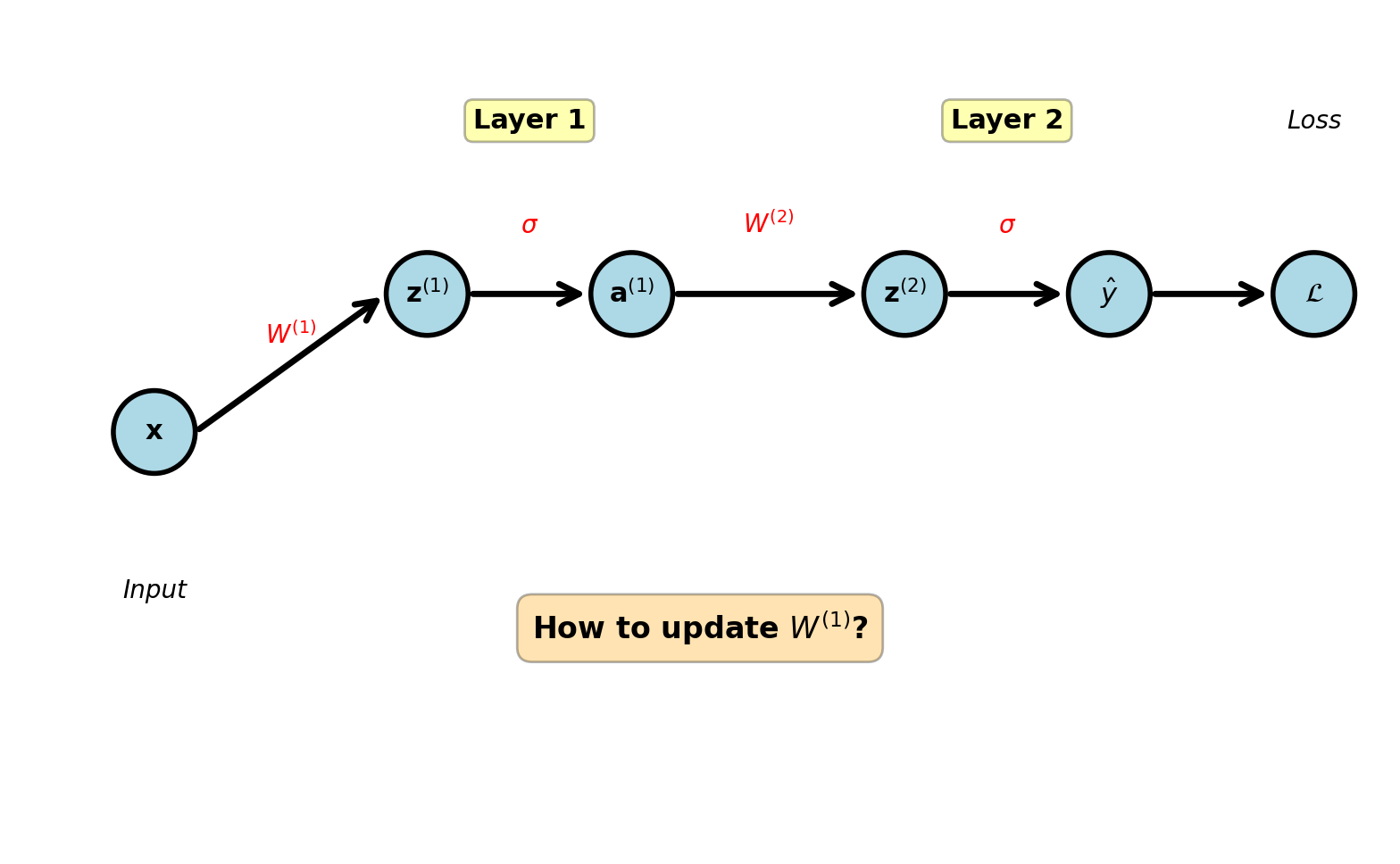
Question: How to update \(W^{(1)}\)?
Answer: \(W^{(1)} \leftarrow W^{(1)} - \eta \frac{\partial \mathcal{L}}{\partial W^{(1)}}\)
Loss depends on \(W^{(1)}\) through path: \[\mathcal{L} \leftarrow \hat{y} \leftarrow \mathbf{z}^{(2)} \leftarrow \mathbf{a}^{(1)} \leftarrow \mathbf{z}^{(1)} \leftarrow W^{(1)}\]
Need systematic method for arbitrary depth
Backpropagation Makes Deep Networks Tractable
Symbolic differentiation:
Expand \(\mathcal{L}\) as function of inputs, differentiate
Example with 3 layers: \[\mathcal{L}(W^{(1)}, W^{(2)}, W^{(3)}) = f^{(3)}(W^{(3)}f^{(2)}(W^{(2)}f^{(1)}(W^{(1)}\mathbf{x})))\]
Applying chain rule symbolically: \[\frac{\partial \mathcal{L}}{\partial W^{(1)}} = \frac{\partial f^{(3)}}{\partial f^{(2)}} \cdot \frac{\partial f^{(2)}}{\partial f^{(1)}} \cdot \frac{\partial f^{(1)}}{\partial W^{(1)}}\]
Problem: Expression size grows exponentially
- Layer \(L\): \(O(2^L)\) terms due to chain rule expansion
- For \(L=50\): \(2^{50} \approx 10^{15}\) terms
- Infeasible to store or compute
Numerical differentiation:
For each parameter \(w_{ij}\): \[\frac{\partial \mathcal{L}}{\partial w_{ij}} \approx \frac{\mathcal{L}(w_{ij} + \epsilon) - \mathcal{L}(w_{ij} - \epsilon)}{2\epsilon}\]
Requires 2 forward passes per parameter
Example network:
- Layer 1: 784 → 256 (200,704 parameters)
- Layer 2: 256 → 128 (32,768 parameters)
- Layer 3: 128 → 10 (1,280 parameters)
Total parameters: \(n = 234{,}752\)
Gradient computation cost:
- Numerical: \(2n = 469{,}504\) forward passes
- Backpropagation: 3 forward passes
Speedup: \(156{,}501\times\)
Modern networks:
- ResNet-50: 25M parameters
- GPT-3: 175B parameters
- Numerical differentiation completely infeasible
Must reuse intermediate computations
Both approaches fail:
- Symbolic: Exponential expression growth
- Numerical: Linear cost in parameters
- Need: Constant cost independent of parameter count
Scalar Chain Rule
For \(y = f(g(x))\): \[\frac{dy}{dx} = \frac{df}{dg} \cdot \frac{dg}{dx}\]
Example: \(y = \sigma(wx + b)\) with \(w=2, b=1, x=0.5\)
Forward: \[z = 2(0.5) + 1 = 2\] \[y = \sigma(2) = 0.881\]
Derivative: \[\frac{dy}{dx} = \frac{dy}{dz} \cdot \frac{dz}{dx} = \sigma'(2) \cdot 2 = 0.881(1-0.881) \cdot 2 = 0.210\]
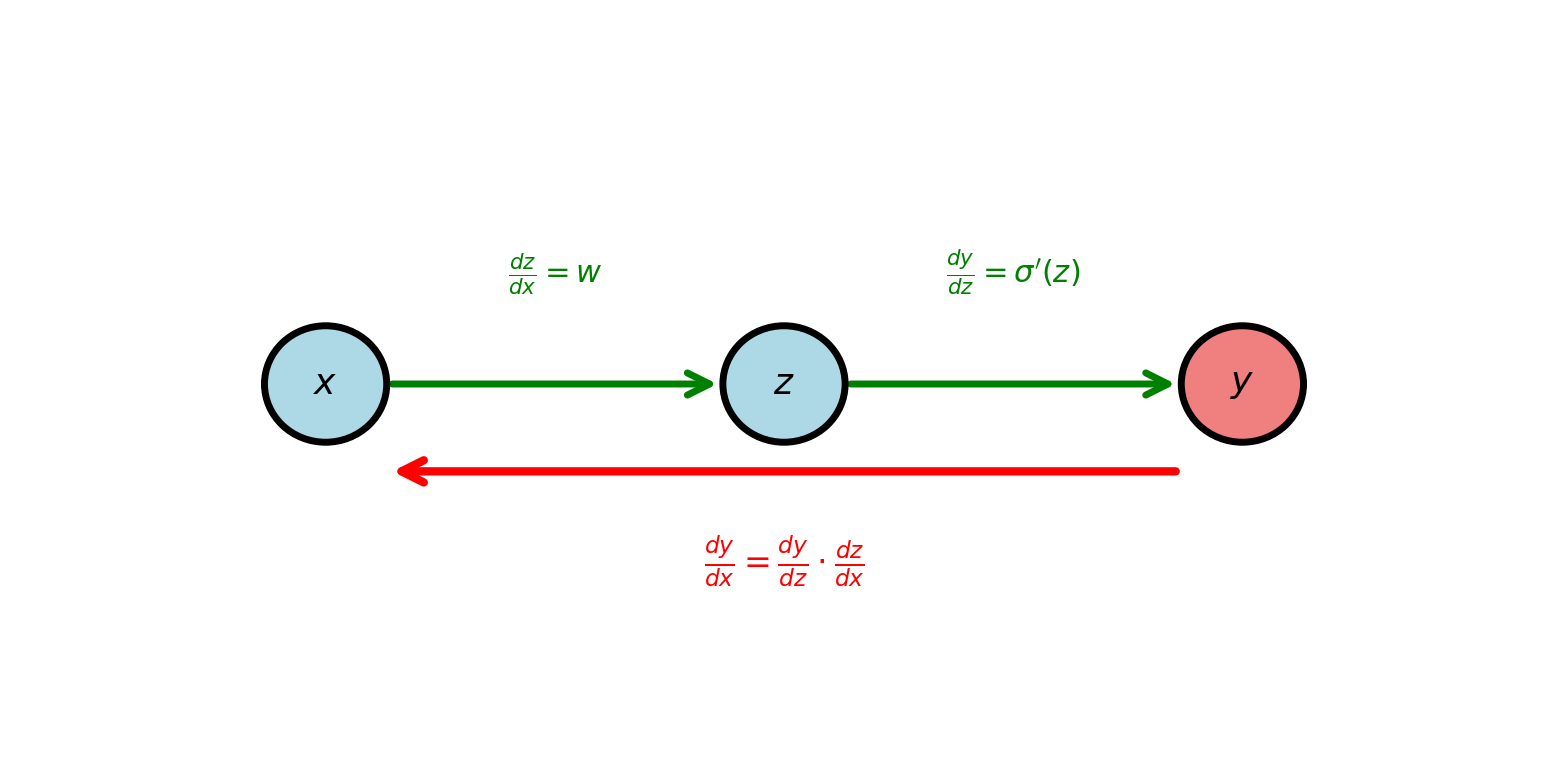
Chain rule: Multiply derivatives along path
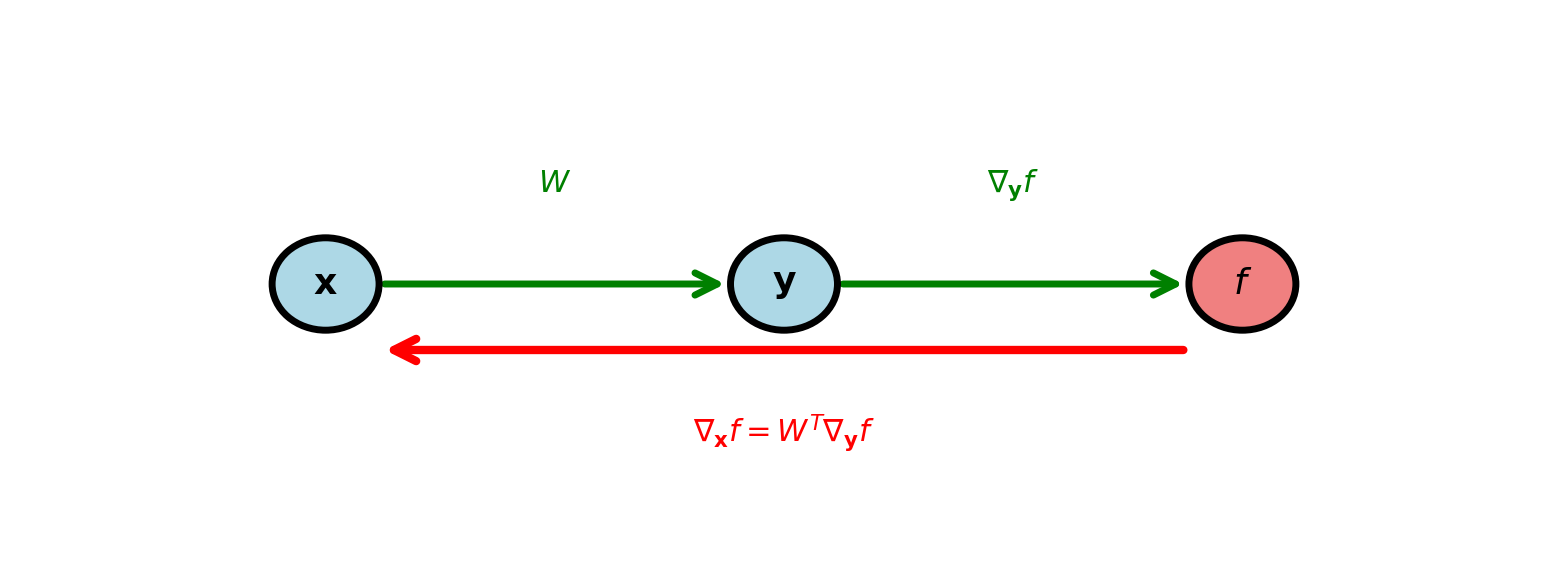
Vector Chain Rule
For \(f: \mathbb{R}^m \to \mathbb{R}\) and \(\mathbf{y} = \mathbf{g}(\mathbf{x})\) where \(\mathbf{g}: \mathbb{R}^n \to \mathbb{R}^m\):
\[\frac{\partial f}{\partial x_i} = \sum_{j=1}^m \frac{\partial f}{\partial y_j} \frac{\partial y_j}{\partial x_i} \quad \Longleftrightarrow \quad \nabla_{\mathbf{x}} f = \left(\frac{\partial \mathbf{y}}{\partial \mathbf{x}}\right)^T \nabla_{\mathbf{y}} f\]
Jacobian \(\frac{\partial \mathbf{y}}{\partial \mathbf{x}} \in \mathbb{R}^{m \times n}\) transpose propagates gradients backward
Example: Composition \(g(\mathbf{y}(\mathbf{x}))\) where
- \(\mathbf{y} = W\mathbf{x}\) (linear transform)
- \(g(\mathbf{y}) = \mathbf{y}^T\mathbf{y}\) (squared norm)
\[W = \begin{bmatrix} 0.5 & 0.3 \\ -0.2 & 0.4 \end{bmatrix}, \quad \mathbf{x} = \begin{bmatrix} 1 \\ 2 \end{bmatrix}\]
Forward: \[\mathbf{y} = \begin{bmatrix} 1.1 \\ 0.6 \end{bmatrix}, \quad g = 1.57\]
Gradient w.r.t. \(\mathbf{y}\): \[\nabla_{\mathbf{y}} g = 2\mathbf{y} = \begin{bmatrix} 2.2 \\ 1.2 \end{bmatrix}\]
Gradient w.r.t. \(\mathbf{x}\) (via chain rule): \[\nabla_{\mathbf{x}} g = W^T \nabla_{\mathbf{y}} g = \begin{bmatrix} 0.5 & -0.2 \\ 0.3 & 0.4 \end{bmatrix} \begin{bmatrix} 2.2 \\ 1.2 \end{bmatrix} = \begin{bmatrix} 0.86 \\ 1.14 \end{bmatrix}\]
Forward Pass Information Flow
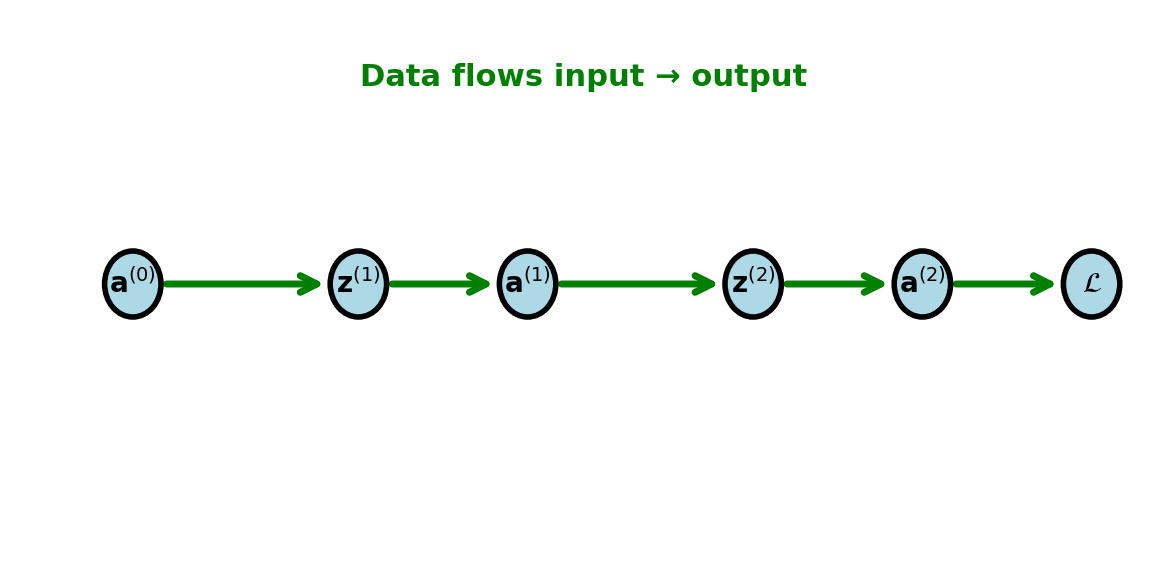
Forward computation:
Starting from \(\mathbf{a}^{(0)} = \mathbf{x}\):
For \(l = 1, 2, \ldots, L\): \[\begin{align} \mathbf{z}^{(l)} &= W^{(l)}\mathbf{a}^{(l-1)} + \mathbf{b}^{(l)}\\ \mathbf{a}^{(l)} &= \sigma^{(l)}(\mathbf{z}^{(l)}) \end{align}\]
Finally: \(\mathcal{L} = \mathcal{L}(\mathbf{a}^{(L)}, \mathbf{y})\)
Must store all \(\mathbf{a}^{(l)}\) and \(\mathbf{z}^{(l)}\) for backward pass:
- \(\mathbf{z}^{(l)}\) for activation derivatives
- \(\mathbf{a}^{(l-1)}\) for weight gradients
Storage requirement: \(O(\sum_{l=1}^L n_l)\) for all activations
Backward Pass Information Flow
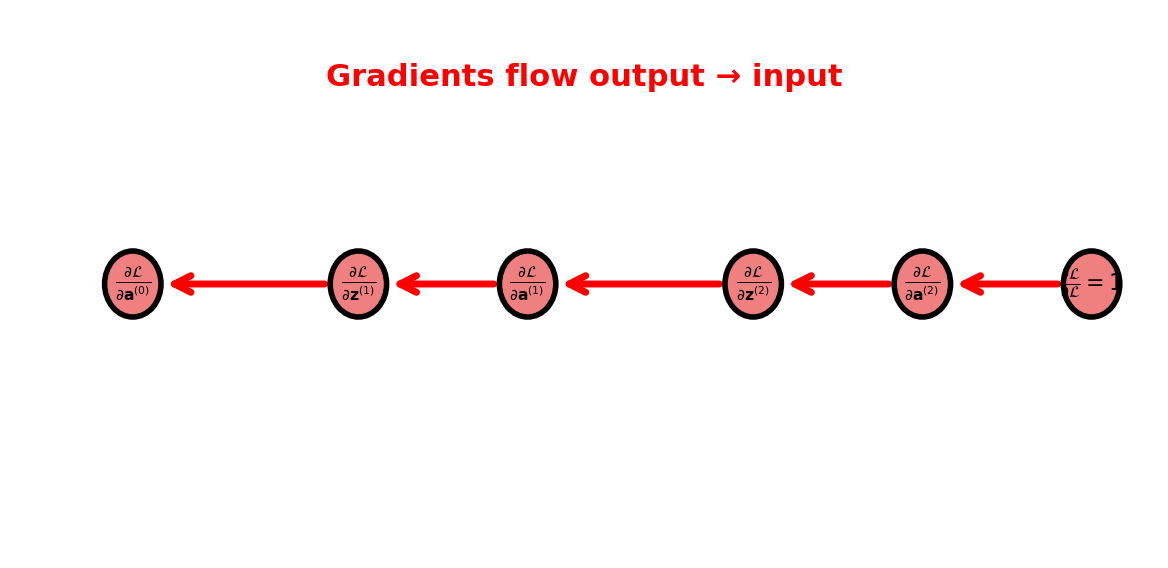
Backward computation:
Starting from \(\frac{\partial \mathcal{L}}{\partial \mathbf{a}^{(L)}}\):
For \(l = L, L-1, \ldots, 1\): \[\begin{align} \frac{\partial \mathcal{L}}{\partial \mathbf{z}^{(l)}} &= \frac{\partial \mathcal{L}}{\partial \mathbf{a}^{(l)}} \odot \sigma'^{(l)}(\mathbf{z}^{(l)})\\ \frac{\partial \mathcal{L}}{\partial W^{(l)}} &= \frac{\partial \mathcal{L}}{\partial \mathbf{z}^{(l)}} (\mathbf{a}^{(l-1)})^T\\ \frac{\partial \mathcal{L}}{\partial \mathbf{a}^{(l-1)}} &= (W^{(l)})^T \frac{\partial \mathcal{L}}{\partial \mathbf{z}^{(l)}} \end{align}\]
Same graph, opposite direction
Complexity of backward ≈ Complexity of forward
Modular Layer Structure
Each layer implements two operations:
forward(input):
- Compute output from input
- Cache input and intermediate values
- Return output
backward(grad_output):
- Receive gradient w.r.t. output
- Compute gradient w.r.t. input
- Compute gradient w.r.t. parameters
- Return gradient w.r.t. input

Example: Linear layer
class Linear:
def forward(self, a_prev):
self.a_prev = a_prev # cache
self.z = W @ a_prev + b
return self.z
def backward(self, grad_z):
grad_W = grad_z @ a_prev.T
grad_b = grad_z
grad_a_prev = W.T @ grad_z
return grad_a_prevExample: Sigmoid layer
class Sigmoid:
def forward(self, z):
self.a = 1 / (1 + np.exp(-z))
return self.a
def backward(self, grad_a):
grad_z = grad_a * self.a * (1 - self.a)
return grad_zEach module only needs its own inputs/outputs
No module needs global network structure
Backpropagation Overview
Network with \(L\) layers:
\(l \in \{1, 2, \ldots, L\}\), where \(\mathbf{z}^{(l)} = W^{(l)}\mathbf{a}^{(l-1)} + \mathbf{b}^{(l)}\) and \(\mathbf{a}^{(l)} = \sigma^{(l)}(\mathbf{z}^{(l)})\)
Boundary conditions:
- Input \(\mathbf{a}^{(0)} = \mathbf{x} \in \mathbb{R}^{n_0}\)
- Output \(\mathbf{a}^{(L)} = \hat{\mathbf{y}} \in \mathbb{R}^{n_L}\)
- Loss \(\mathcal{L} = \mathcal{L}(\hat{\mathbf{y}}, \mathbf{y})\)
Objective:
Compute \(\frac{\partial \mathcal{L}}{\partial W^{(l)}}\) and \(\frac{\partial \mathcal{L}}{\partial \mathbf{b}^{(l)}}\) for all \(l = 1, \ldots, L\) efficiently
Forward: \(\mathbf{x} \xrightarrow{W^{(1)}} \mathbf{h} \xrightarrow{W^{(2)}} \hat{\mathbf{y}} \to \mathcal{L}\)
Store intermediate activations
Backward: \(\frac{\partial \mathcal{L}}{\partial W^{(1)}} \xleftarrow{} \frac{\partial \mathcal{L}}{\partial W^{(2)}} \xleftarrow{} \frac{\partial \mathcal{L}}{\partial \hat{\mathbf{y}}}\)
Update (\(\forall l = 1, \ldots, L\)): \[W^{(l)} \leftarrow W^{(l)} - \eta \frac{\partial \mathcal{L}}{\partial W^{(l)}}\] \[\mathbf{b}^{(l)} \leftarrow \mathbf{b}^{(l)} - \eta \frac{\partial \mathcal{L}}{\partial \mathbf{b}^{(l)}}\]
Dimensions: \(W^{(l)} \in \mathbb{R}^{n_l \times n_{l-1}}\), \(\mathbf{a}^{(l)}, \mathbf{z}^{(l)}, \mathbf{b}^{(l)} \in \mathbb{R}^{n_l}\)
Chain rule applied systematically from output to input
Scalar Networks
Simplest Deep Network
Architecture: Two-layer scalar network
\[x \xrightarrow{w_1} s_1 \xrightarrow{\sigma} a_1 \xrightarrow{w_2} s_2 \xrightarrow{\sigma} \hat{y}\]
One scalar value per layer
Parameters:
- \(w_1 = 0.5\), \(b_1 = 0\)
- \(w_2 = -1\), \(b_2 = 0.5\)
Data:
- Input: \(x = 2\)
- Target: \(y = 1\)
Goal: Compute all gradients
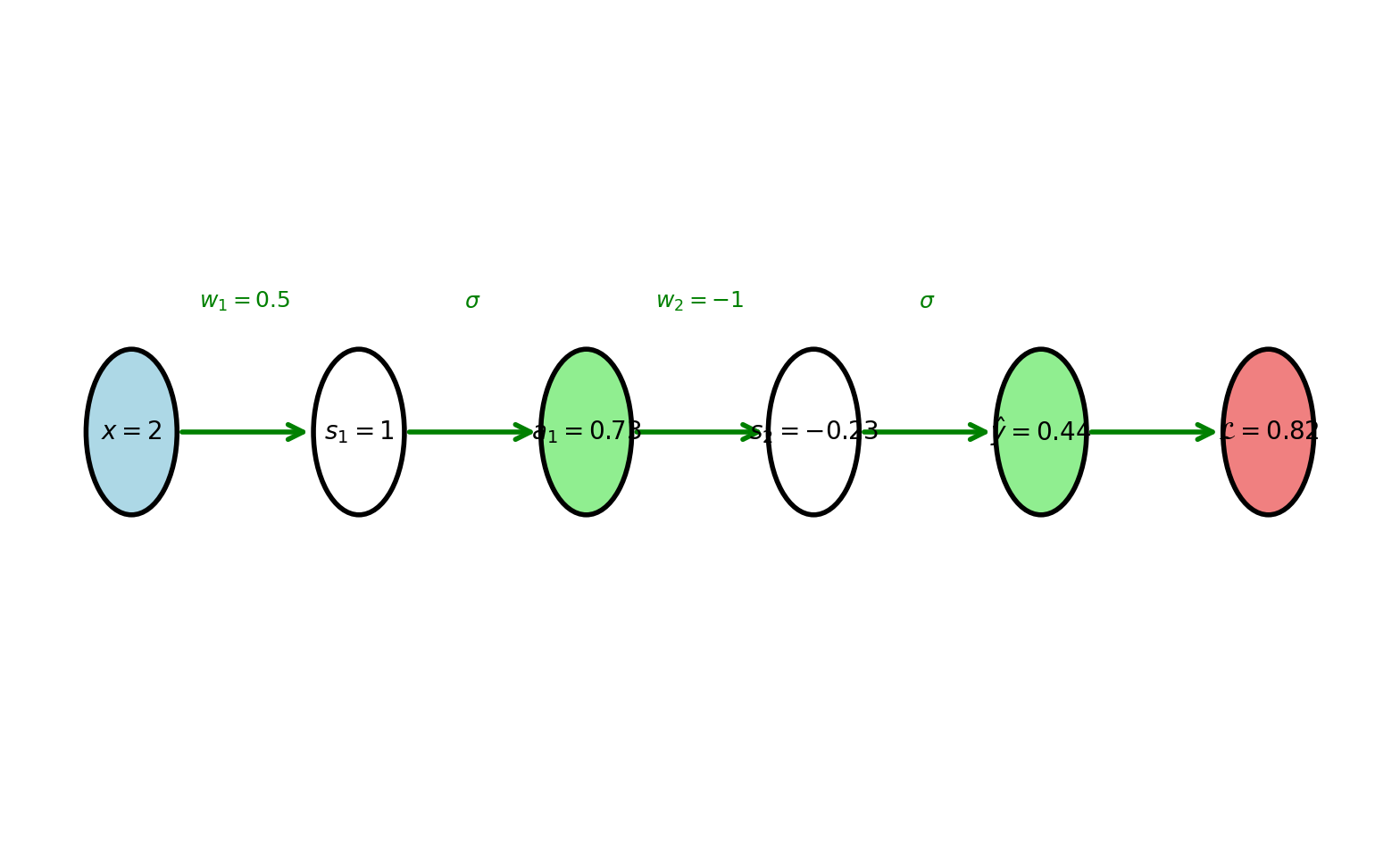
Forward values computed left to right
Forward Pass Computation
Layer 1:
\[s_1 = w_1 x + b_1 = 0.5(2) + 0 = 1\]
\[a_1 = \sigma(1) = \frac{1}{1+e^{-1}} = 0.731\]
Layer 2:
\[s_2 = w_2 a_1 + b_2 = -1(0.731) + 0.5 = -0.231\]
\[\hat{y} = \sigma(-0.231) = 0.442\]
Loss (binary cross-entropy, \(y=1\)):
\[\mathcal{L} = -\log(\hat{y}) = -\log(0.442) = 0.816\]
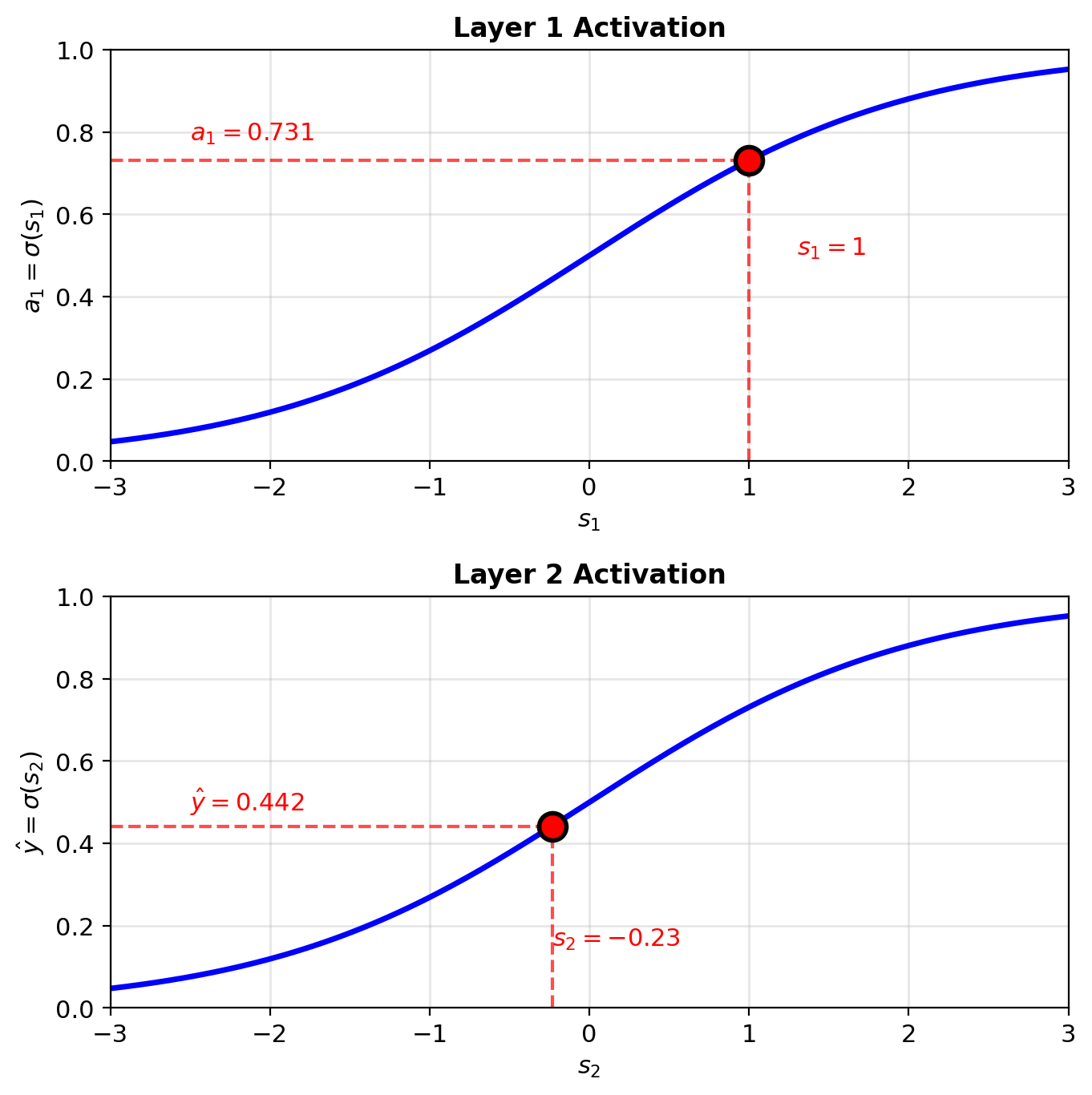
Sigmoid evaluation at specific pre-activation values
Backward Pass: Output Layer
Gradient w.r.t. \(\hat{y}\):
\[\frac{\partial \mathcal{L}}{\partial \hat{y}} = -\frac{y}{\hat{y}} + \frac{1-y}{1-\hat{y}} = -\frac{1}{0.442} = -2.262\]
Through sigmoid (\(\sigma'(z) = \sigma(z)(1-\sigma(z))\)):
\[\frac{\partial \hat{y}}{\partial s_2} = 0.442(1-0.442) = 0.247\]
Chain rule:
\[\frac{\partial \mathcal{L}}{\partial s_2} = -2.262 \times 0.247 = -0.558\]
Weight gradient:
\[\frac{\partial \mathcal{L}}{\partial w_2} = \frac{\partial \mathcal{L}}{\partial s_2} \times a_1 = -0.558 \times 0.731 = -0.408\]
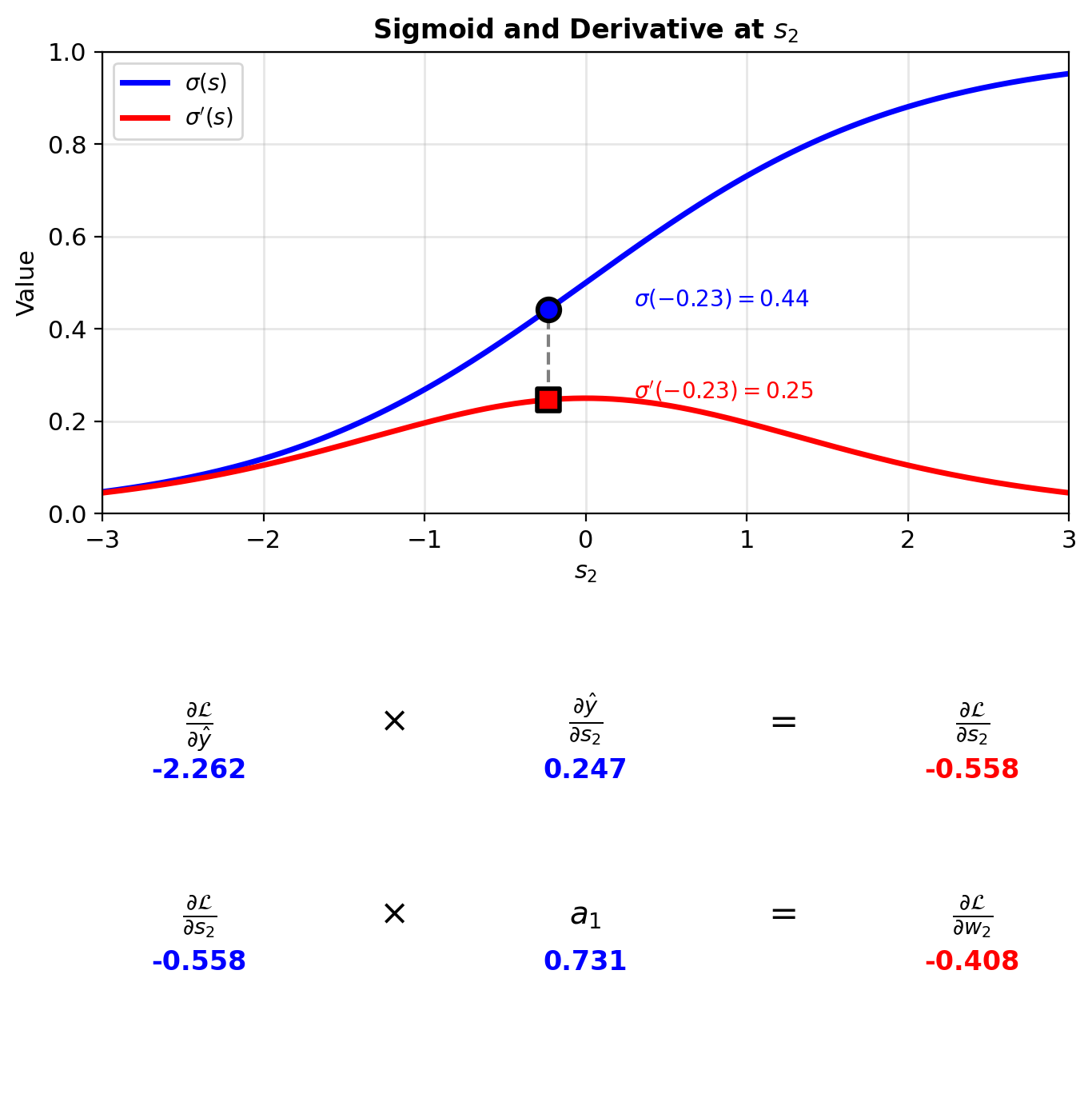
Delta Notation
Define: \(\delta^{(l)} \equiv \frac{\partial \mathcal{L}}{\partial s^{(l)}}\) (gradient w.r.t. pre-activation)
Why useful: Appears repeatedly in gradient computation
For our network:
Output layer: \[\delta^{(2)} = \frac{\partial \mathcal{L}}{\partial s_2} = -0.558\]
Hidden layer: \[\delta^{(1)} = \frac{\partial \mathcal{L}}{\partial s_1} = ?\]
Weight gradients simplify:
\[\frac{\partial \mathcal{L}}{\partial w_2} = \delta^{(2)} \cdot a_1 = -0.558 \times 0.731 = -0.408\]
\[\frac{\partial \mathcal{L}}{\partial b_2} = \delta^{(2)} = -0.558\]

Backward Pass: Hidden Layer
Gradient flows back through weight:
\[\frac{\partial \mathcal{L}}{\partial a_1} = \delta^{(2)} \times w_2 = -0.558 \times (-1) = 0.558\]
Through sigmoid:
\[\frac{\partial a_1}{\partial s_1} = a_1(1-a_1) = 0.731(0.269) = 0.197\]
\[\delta^{(1)} = \frac{\partial \mathcal{L}}{\partial s_1} = 0.558 \times 0.197 = 0.110\]
Weight gradient:
\[\frac{\partial \mathcal{L}}{\partial w_1} = \delta^{(1)} \times x = 0.110 \times 2 = 0.220\]
All gradients:
- \(\frac{\partial \mathcal{L}}{\partial w_2} = -0.408\), \(\frac{\partial \mathcal{L}}{\partial b_2} = \delta^{(2)} = -0.558\)
- \(\frac{\partial \mathcal{L}}{\partial w_1} = 0.220\), \(\frac{\partial \mathcal{L}}{\partial b_1} = \delta^{(1)} = 0.110\)
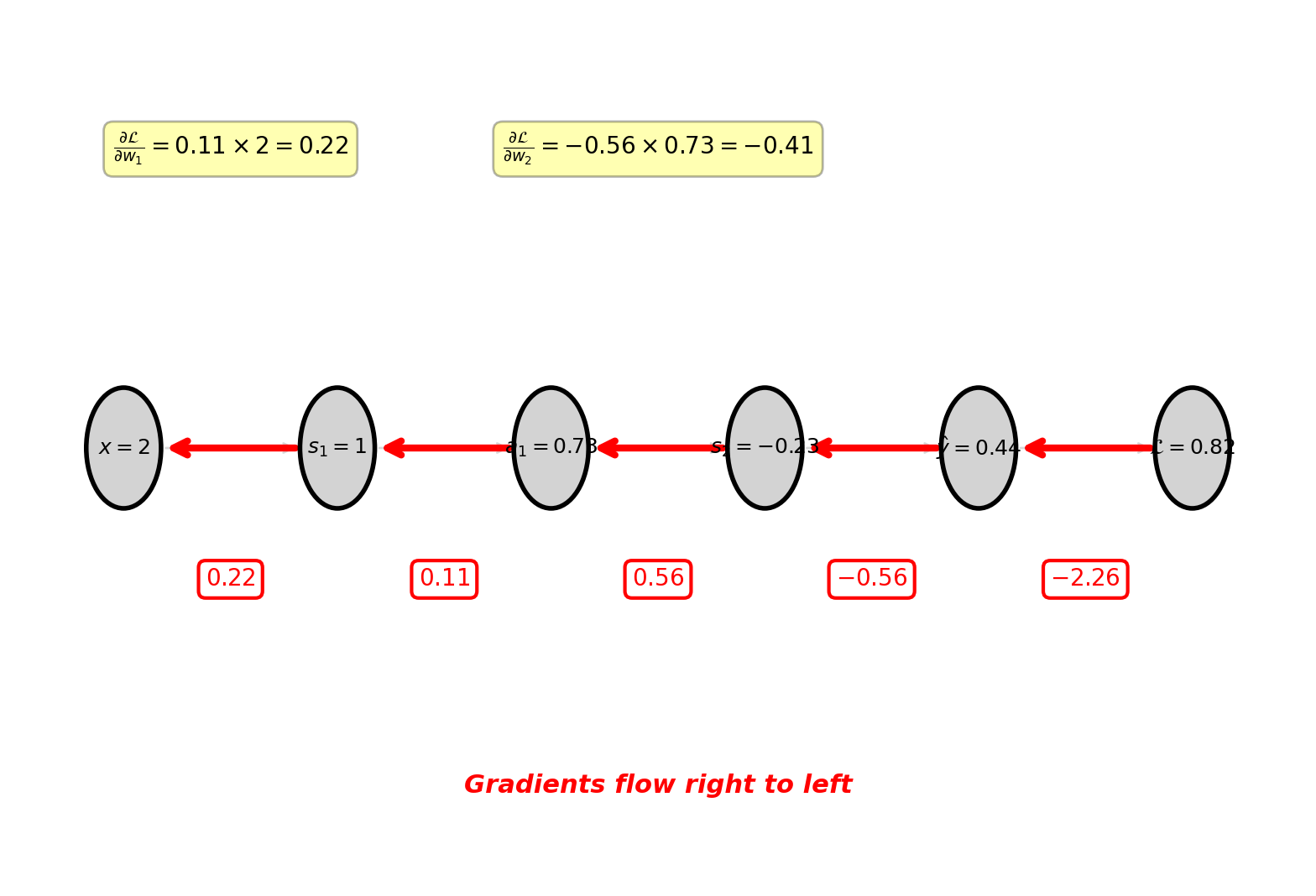
Gradients propagate backward, multiplying at each stage
Backpropagation Flow: Scalar Network
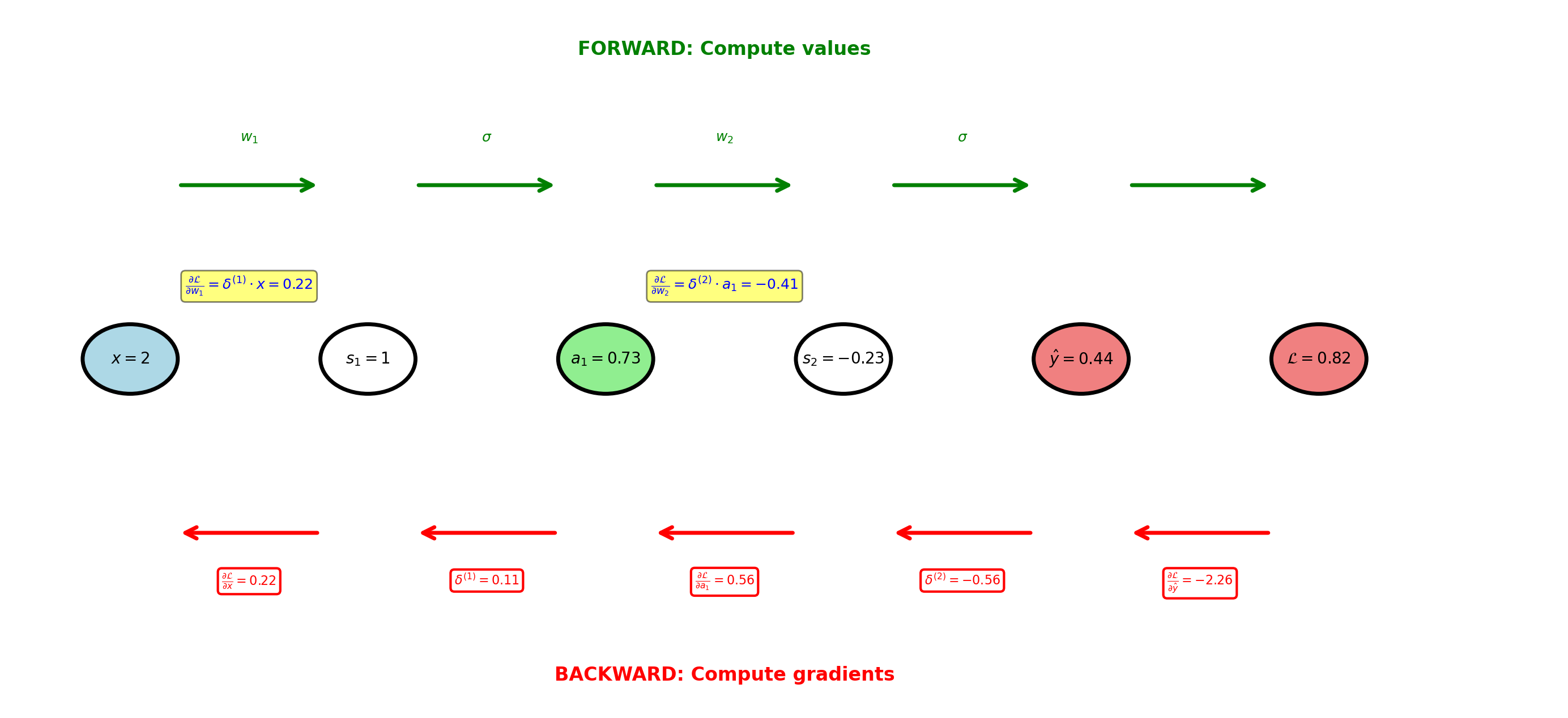
Forward pass computes values, backward pass computes gradients using chain rule
Three Problems
Problem 1: Initialize gradient w.r.t. pre-activation
How to compute \(\frac{\partial \mathcal{L}}{\partial s^{(L)}}\) at output layer?
Problem 2: Propagate gradient backward one layer
Given \(\frac{\partial \mathcal{L}}{\partial s^{(l+1)}}\), compute \(\frac{\partial \mathcal{L}}{\partial s^{(l)}}\)
Problem 3: Compute parameter gradients
Given \(\frac{\partial \mathcal{L}}{\partial s^{(l)}}\), compute \(\frac{\partial \mathcal{L}}{\partial w_l}\) and \(\frac{\partial \mathcal{L}}{\partial b_l}\)
Using \(\delta^{(l)} \equiv \frac{\partial \mathcal{L}}{\partial s^{(l)}}\):
Problem 1: Compute \(\delta^{(L)}\) \[\delta^{(L)} = \frac{\partial \mathcal{L}}{\partial \hat{y}} \cdot \sigma'(s^{(L)})\]
Problem 2: Compute \(\delta^{(l)}\) from \(\delta^{(l+1)}\) \[\delta^{(l)} = \delta^{(l+1)} \cdot w_{l+1} \cdot \sigma'(s^{(l)})\]
Problem 3: Compute gradients from \(\delta^{(l)}\) \[\frac{\partial \mathcal{L}}{\partial w_l} = \delta^{(l)} \cdot a^{(l-1)}\] \[\frac{\partial \mathcal{L}}{\partial b_l} = \delta^{(l)}\]
Network with Branching
Architecture: Two hidden units
\[x \to \begin{cases} h_1 = \sigma(w_1 x + b_1) \\ h_2 = \sigma(w_2 x + b_2) \end{cases} \to y = w_3 h_1 + w_4 h_2\]
Parameters: \(w_1 = 0.5, w_2 = -0.3, w_3 = 1, w_4 = 1\), all biases zero
Data: \(x = 1\), target \(t = 0.5\)
Forward:
\(h_1 = \sigma(0.5) = 0.622\)
\(h_2 = \sigma(-0.3) = 0.426\)
\(y = 0.622 + 0.426 = 1.048\)
Loss: \(\mathcal{L} = \frac{1}{2}(1.048 - 0.5)^2 = 0.150\)
Backward: \(\frac{\partial \mathcal{L}}{\partial y} = 1.048 - 0.5 = 0.548\)
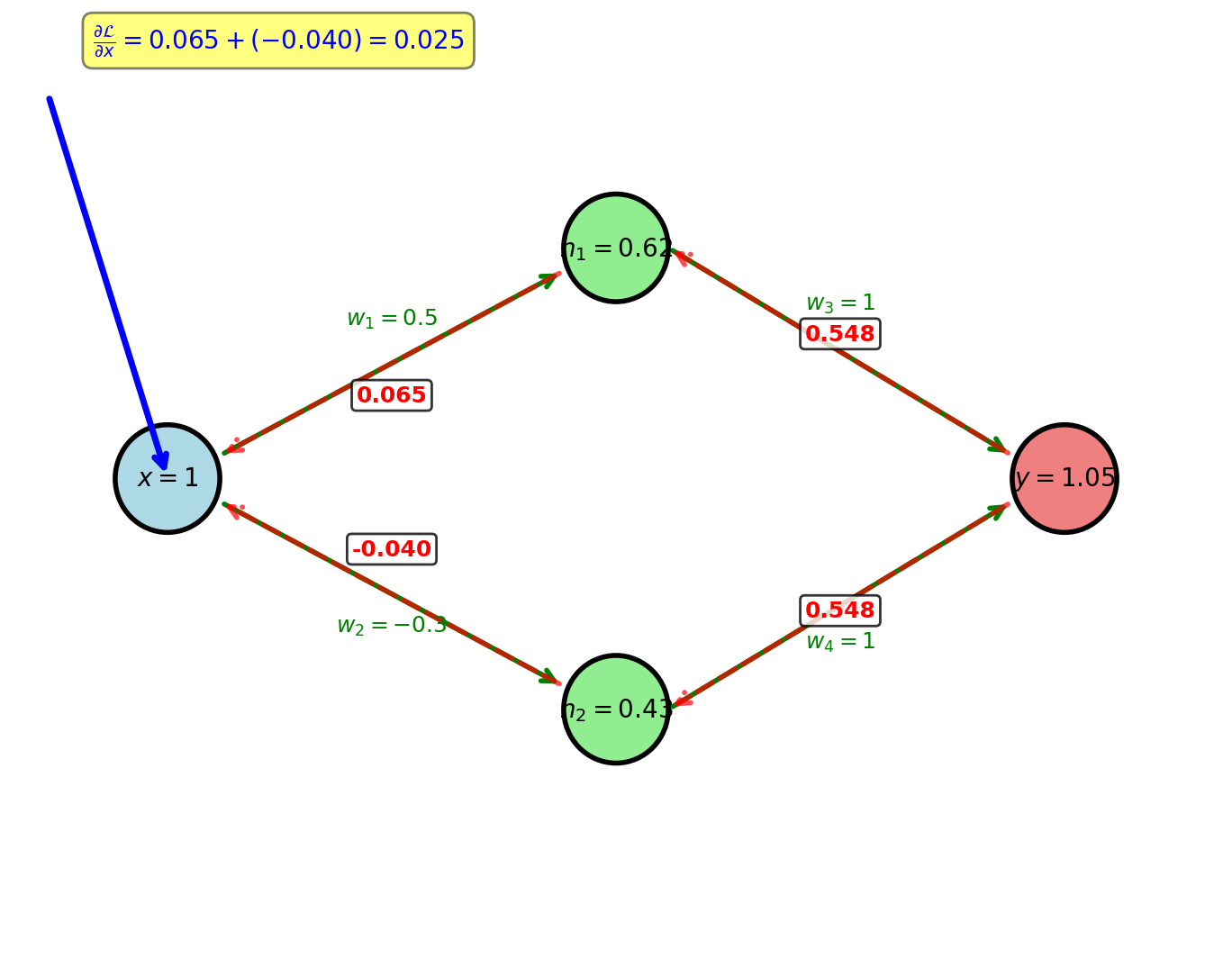
Multiple gradient paths converge at \(x\)
Gradient Accumulation Rule
Multivariate chain rule:
Two paths from \(\mathcal{L}\) to \(x\):
\[\frac{\partial \mathcal{L}}{\partial x} = \frac{\partial \mathcal{L}}{\partial h_1}\frac{\partial h_1}{\partial x} + \frac{\partial \mathcal{L}}{\partial h_2}\frac{\partial h_2}{\partial x}\]
Path 1 contribution:
\[\frac{\partial \mathcal{L}}{\partial y} = y - t = 1.048 - 0.5 = 0.548\]
\[\frac{\partial \mathcal{L}}{\partial h_1} = \frac{\partial \mathcal{L}}{\partial y} \cdot \frac{\partial y}{\partial h_1} = 0.548 \cdot w_3 = 0.548 \cdot 1 = 0.548\]
\[\frac{\partial h_1}{\partial x} = \sigma'(w_1 x) \cdot w_1 = 0.622(0.378) \cdot 0.5 = 0.118\]
\[\text{Contribution}_1 = 0.548 \cdot 0.118 = 0.065\]
Path 2 contribution:
\[\frac{\partial \mathcal{L}}{\partial h_2} = \frac{\partial \mathcal{L}}{\partial y} \cdot \frac{\partial y}{\partial h_2} = 0.548 \cdot w_4 = 0.548 \cdot 1 = 0.548\]
\[\frac{\partial h_2}{\partial x} = \sigma'(w_2 x) \cdot w_2 = 0.426(0.574) \cdot (-0.3) = -0.073\]
\[\text{Contribution}_2 = 0.548 \cdot (-0.073) = -0.040\]
Total gradient:
\[\frac{\partial \mathcal{L}}{\partial x} = 0.065 + (-0.040) = 0.025\]
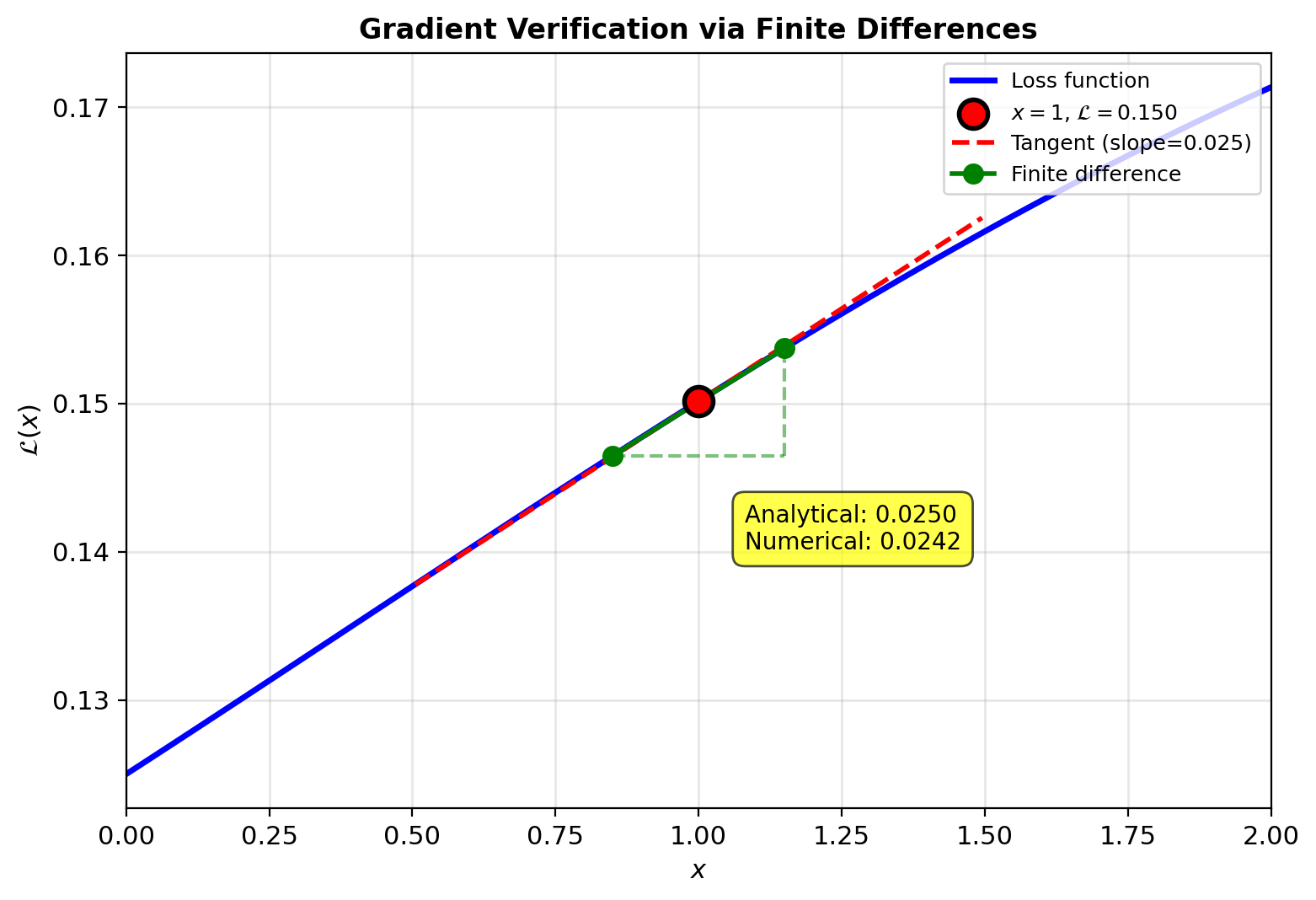
Analytical gradient matches numerical
When multiple paths converge, gradients add
Backpropagation Algorithm: 3-Layer Example
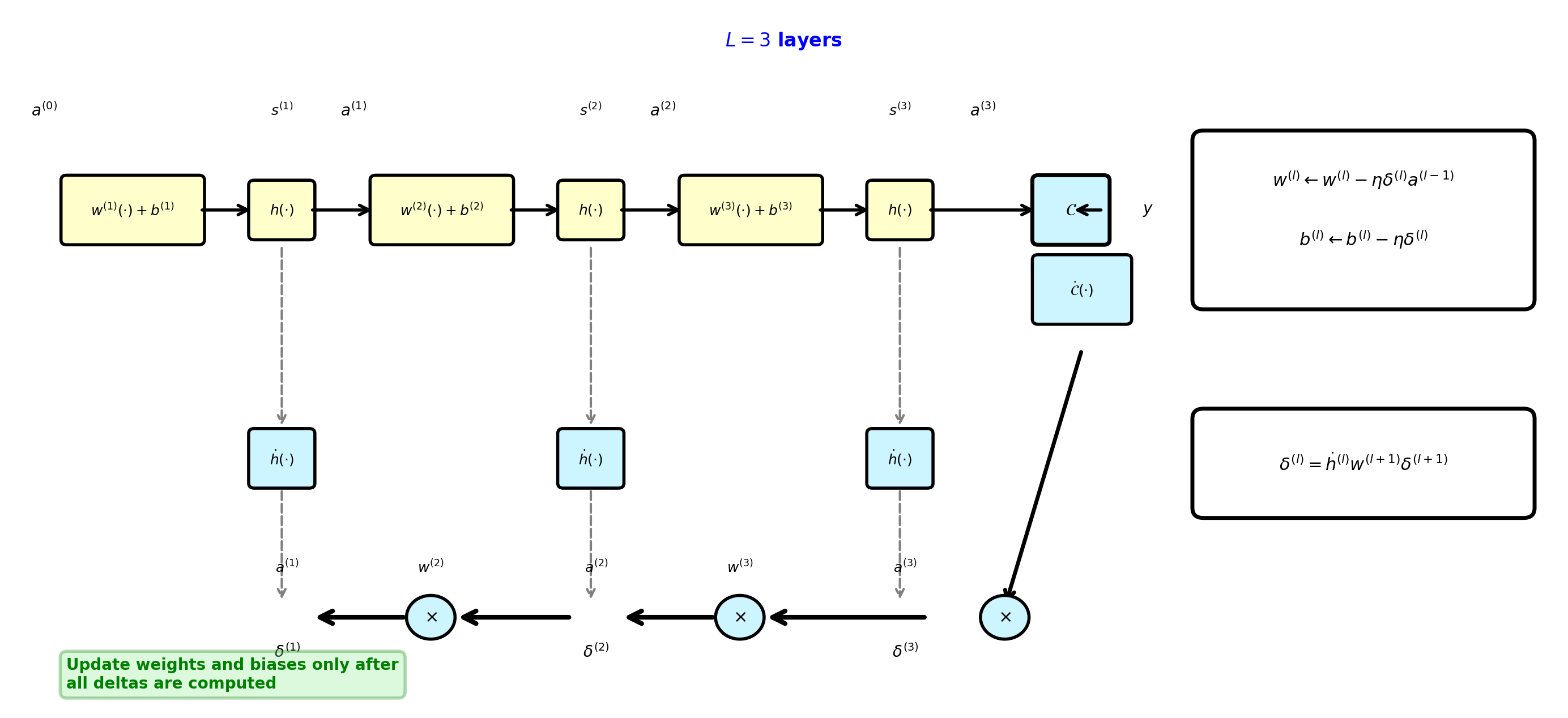
Forward pass computes activations, backward pass computes deltas via recursion, then update all parameters
Scalar Backpropagation Summary
Loss and activation functions:
Loss (binary cross-entropy): \[\mathcal{L} = -[y\log\hat{y} + (1-y)\log(1-\hat{y})]\]
Sigmoid activation: \[\sigma(s) = \frac{1}{1+e^{-s}}\]
Derivatives:
Loss derivative: \[\frac{\partial \mathcal{L}}{\partial \hat{y}} = -\frac{y}{\hat{y}} + \frac{1-y}{1-\hat{y}}\]
Sigmoid derivative: \[\sigma'(s) = \sigma(s)(1-\sigma(s))\]
Backpropagation formulas:
Define: \(\delta^{(l)} = \frac{\partial \mathcal{L}}{\partial s^{(l)}}\)
Output layer: \[\delta^{(L)} = \frac{\partial \mathcal{L}}{\partial \hat{y}} \cdot \sigma'(s^{(L)})\]
Hidden layers: \[\delta^{(l)} = \delta^{(l+1)} \cdot w_{l+1} \cdot \sigma'(s^{(l)})\]
Parameter updates: \[w \leftarrow w - \eta \delta \cdot a^{(l-1)}\] \[b \leftarrow b - \eta \delta\]
Each gradient: upstream \(\times\) local derivative
Vector and Matrix Formulation
Two-Layer Network Architecture
Scalar to vector: Binary classification (1 output) → Multi-class classification (K outputs)
Sigmoid: \(\hat{y} = \sigma(s) \in (0,1)\) (probability of class 1)
Softmax: \(\hat{\mathbf{y}} = \text{softmax}(\mathbf{s}) \in \mathbb{R}^K\), \(\sum_i \hat{y}_i = 1\) (probability distribution over K classes)
Dimensions:
- Input: \(\mathbf{x} \in \mathbb{R}^3\)
- Hidden: \(\mathbf{h} \in \mathbb{R}^4\)
- Output: \(\mathbf{y} \in \mathbb{R}^2\) (2-class example)
Parameters:
Layer 1:
- \(W^{(1)} \in \mathbb{R}^{4 \times 3}\): 12 weights
- \(\mathbf{b}^{(1)} \in \mathbb{R}^4\): 4 biases
Layer 2:
- \(W^{(2)} \in \mathbb{R}^{2 \times 4}\): 8 weights
- \(\mathbf{b}^{(2)} \in \mathbb{R}^2\): 2 biases
Total: 26 parameters
Forward pass:
\[\mathbf{s}^{(1)} = W^{(1)}\mathbf{x} + \mathbf{b}^{(1)}, \quad \mathbf{a}^{(1)} = \sigma(\mathbf{s}^{(1)})\] \[\mathbf{s}^{(2)} = W^{(2)}\mathbf{a}^{(1)} + \mathbf{b}^{(2)}, \quad \mathbf{a}^{(2)} = \text{softmax}(\mathbf{s}^{(2)})\]

Fully connected: every unit in one layer connects to every unit in next layer
Matrix Form: Element-Wise View
Compact notation: \[\mathbf{z}^{(1)} = W^{(1)}\mathbf{x} + \mathbf{b}^{(1)}\]
Expanded (element-wise) (3 → 4 example): \[\begin{bmatrix} z_1^{(1)}\\ z_2^{(1)}\\ z_3^{(1)}\\ z_4^{(1)} \end{bmatrix} = \begin{bmatrix} w_{11}^{(1)} & w_{12}^{(1)} & w_{13}^{(1)}\\ w_{21}^{(1)} & w_{22}^{(1)} & w_{23}^{(1)}\\ w_{31}^{(1)} & w_{32}^{(1)} & w_{33}^{(1)}\\ w_{41}^{(1)} & w_{42}^{(1)} & w_{43}^{(1)} \end{bmatrix} \begin{bmatrix} x_1\\ x_2\\ x_3 \end{bmatrix} + \begin{bmatrix} b_1^{(1)}\\ b_2^{(1)}\\ b_3^{(1)}\\ b_4^{(1)} \end{bmatrix}\]
Which weights affect given output?
Element \(z_i^{(1)}\) depends on:
All inputs: \(x_1, x_2, x_3\)
One row of \(W^{(1)}\): \(w_{i1}^{(1)}, w_{i2}^{(1)}, w_{i3}^{(1)}\)
One bias: \(b_i^{(1)}\)
\[z_i^{(1)} = \sum_{j=1}^3 w_{ij}^{(1)} x_j + b_i^{(1)}\]
Gradient \(\frac{\partial \mathcal{L}}{\partial w_{ij}^{(1)}}\) affects only \(z_i^{(1)}\)
Rest of backprop: how changes in \(z_i^{(1)}\) affect loss \(\mathcal{L}\)
Forward Pass: Dimension Tracking
Layer 1:
Pre-activation: \[\mathbf{s}^{(1)} = W^{(1)}\mathbf{x} + \mathbf{b}^{(1)}\]
Dimensions: \[[4 \times 1] = [4 \times 3][3 \times 1] + [4 \times 1]\]
Activation (element-wise): \[\mathbf{a}^{(1)} = \sigma(\mathbf{s}^{(1)})\] \[[4 \times 1] = \sigma([4 \times 1])\]
Layer 2:
Pre-activation: \[\mathbf{s}^{(2)} = W^{(2)}\mathbf{a}^{(1)} + \mathbf{b}^{(2)}\]
Dimensions: \[[2 \times 1] = [2 \times 4][4 \times 1] + [2 \times 1]\]
Softmax (probability distribution): \[\mathbf{a}^{(2)} = \text{softmax}(\mathbf{s}^{(2)})\]
where \([\text{softmax}(\mathbf{s})]_i = \frac{e^{s_i}}{\sum_j e^{s_j}}\)
Note: Each output depends on all inputs, i.e., not element-wise activation
Example computation:
\[W^{(1)} = \begin{bmatrix} 0.1 & 0.2 & -0.1 \\ 0.3 & -0.2 & 0.1 \\ -0.1 & 0.1 & 0.2 \\ 0.2 & 0.3 & -0.3 \end{bmatrix}, \quad \mathbf{x} = \begin{bmatrix} 1.0 \\ 0.5 \\ -0.5 \end{bmatrix}\]
\[\mathbf{s}^{(1)} = \begin{bmatrix} 0.1(1.0) + 0.2(0.5) - 0.1(-0.5) \\ 0.3(1.0) - 0.2(0.5) + 0.1(-0.5) \\ -0.1(1.0) + 0.1(0.5) + 0.2(-0.5) \\ 0.2(1.0) + 0.3(0.5) - 0.3(-0.5) \end{bmatrix} + \begin{bmatrix} 0.1 \\ -0.1 \\ 0.0 \\ 0.2 \end{bmatrix}\]
\[= \begin{bmatrix} 0.25 \\ 0.05 \\ -0.05 \\ 0.55 \end{bmatrix}\]
\[\mathbf{a}^{(1)} = \begin{bmatrix} \sigma(0.25) \\ \sigma(0.05) \\ \sigma(-0.05) \\ \sigma(0.55) \end{bmatrix} = \begin{bmatrix} 0.562 \\ 0.513 \\ 0.488 \\ 0.634 \end{bmatrix}\]
Reminder: Matrix multiplication requires dimension compatibility
Vector Backpropagation: Same Three Problems
Problem 2 (scalar): Propagate \(\delta\) backward one layer
\[\delta^{(l)} = \delta^{(l+1)} \cdot w_{l+1} \cdot \sigma'(s^{(l)})\]
Three scalar multiplications
Problem 2 (vector): Propagate \(\boldsymbol{\delta}\) backward
\[\boldsymbol{\delta}^{(l)} = \, ???\]
Components:
- \(\boldsymbol{\delta}^{(l+1)} \in \mathbb{R}^{n_{l+1}}\) (vector)
- \(W^{(l+1)} \in \mathbb{R}^{n_{l+1} \times n_l}\) (matrix)
- \(\sigma'(\mathbf{s}^{(l)}) \in \mathbb{R}^{n_l}\) (vector)
How do these combine?
Problem 3 (scalar): Weight gradient
\[\frac{\partial \mathcal{L}}{\partial w_l} = \delta^{(l)} \cdot a^{(l-1)}\]
Problem 3 (vector): Weight gradient matrix
\[\frac{\partial \mathcal{L}}{\partial W^{(l)}} = \, ???\]
Dimensions: \(\mathbb{R}^{n_l \times n_{l-1}}\) required
Scalar → Vector translation:
Multiplication (\(\cdot\)) → Matrix multiply or element-wise (\(\odot\))?
Example (3 → 4 → 2 network):
Output layer: \(\boldsymbol{\delta}^{(2)} \in \mathbb{R}^2\) computed
Hidden layer: \(\boldsymbol{\delta}^{(1)} \in \mathbb{R}^4\) = ?
Inputs available:
- \(\boldsymbol{\delta}^{(2)} = [d_1^{(2)}, d_2^{(2)}]^T\) (2 × 1)
- \(W^{(2)} \in \mathbb{R}^{2 \times 4}\)
- \(\sigma'(\mathbf{s}^{(1)}) \in \mathbb{R}^4\) (4 × 1)
Need output: 4 × 1 vector
Matrix dimensions suggest: \((W^{(2)})^T \boldsymbol{\delta}^{(2)}\) gives 4 × 1
But how does \(\sigma'\) combine? Element-wise or matrix?
Need systematic framework for vector derivatives
Jacobian Perspective
Jacobian matrix: All partial derivatives
For \(\mathbf{y} = f(\mathbf{x})\) where \(\mathbf{y} \in \mathbb{R}^m\), \(\mathbf{x} \in \mathbb{R}^n\):
\[J = \frac{\partial \mathbf{y}}{\partial \mathbf{x}} = \begin{bmatrix} \frac{\partial y_1}{\partial x_1} & \cdots & \frac{\partial y_1}{\partial x_n} \\ \vdots & \ddots & \vdots \\ \frac{\partial y_m}{\partial x_1} & \cdots & \frac{\partial y_m}{\partial x_n} \end{bmatrix} \in \mathbb{R}^{m \times n}\]
Linear layer:
\[\mathbf{s} = W\mathbf{a} + \mathbf{b}\]
\[\frac{\partial \mathbf{s}}{\partial \mathbf{a}} = W\]
Element-wise activation:
\[a_i = \sigma(s_i)\]
\[\frac{\partial \mathbf{a}}{\partial \mathbf{s}} = \text{diag}(\sigma'(s_1), \ldots, \sigma'(s_n))\]
Diagonal because \(\frac{\partial a_i}{\partial s_j} = 0\) for \(i \neq j\)
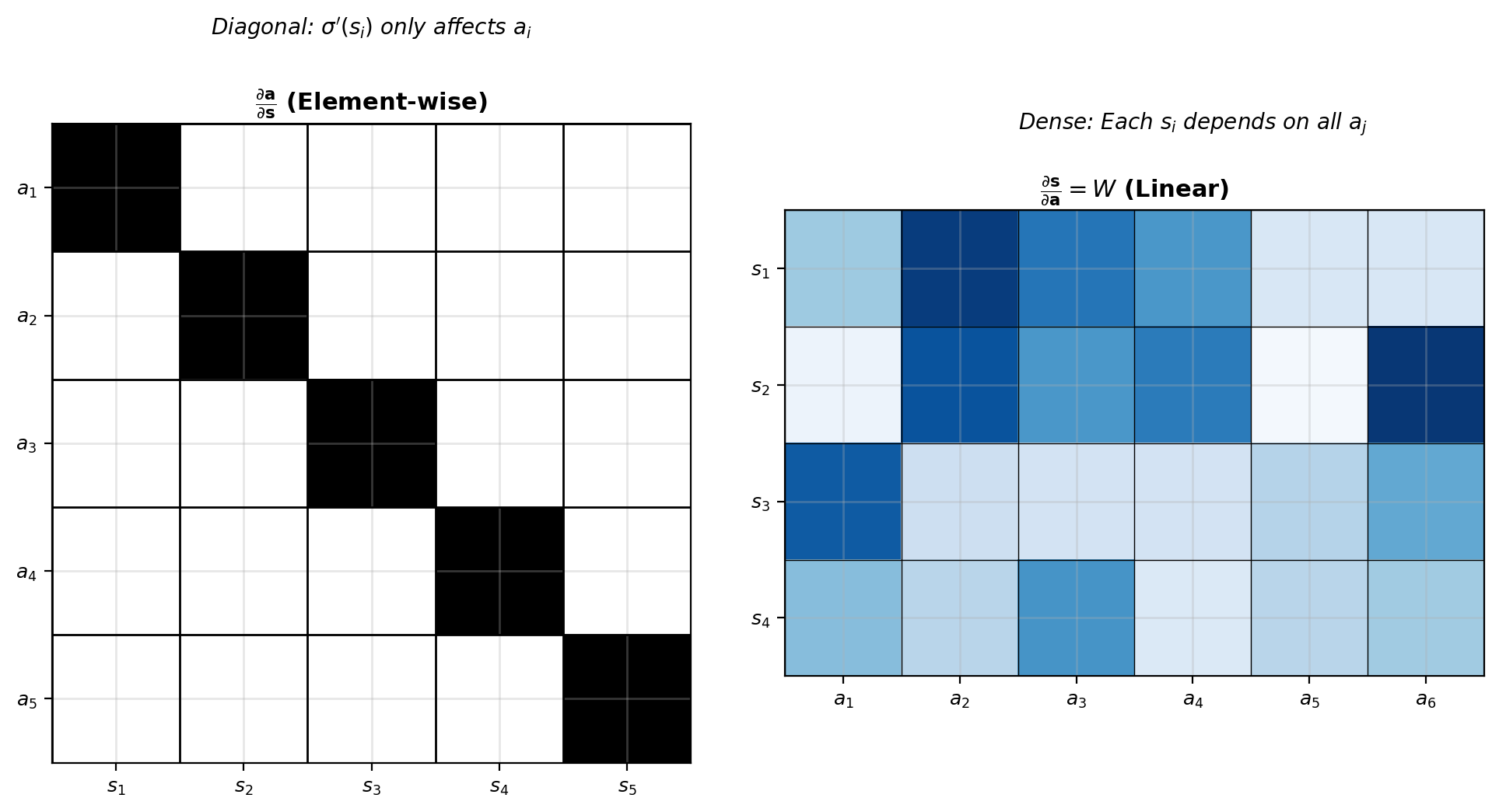
Jacobian structure reflects dependencies
Chain Rule in Matrix Form
Scalar chain rule:
For \(\mathcal{L}(f(g(x)))\): \[\frac{d\mathcal{L}}{dx} = \frac{d\mathcal{L}}{df} \cdot \frac{df}{dg} \cdot \frac{dg}{dx}\]
Vector chain rule:
For \(\mathcal{L}(\mathbf{a}(\mathbf{s}(\mathbf{x})))\) where \(\mathcal{L}: \mathbb{R}^n \to \mathbb{R}\):
\[\nabla_{\mathbf{x}} \mathcal{L} = \left(\frac{\partial \mathbf{s}}{\partial \mathbf{x}}\right)^T \left(\frac{\partial \mathbf{a}}{\partial \mathbf{s}}\right)^T \nabla_{\mathbf{a}} \mathcal{L}\]
Transpose appears from chain rule!
For our network:
\[\frac{\partial \mathcal{L}}{\partial \mathbf{a}^{(l-1)}} = \left(\frac{\partial \mathbf{s}^{(l)}}{\partial \mathbf{a}^{(l-1)}}\right)^T \frac{\partial \mathcal{L}}{\partial \mathbf{s}^{(l)}}\]
\[= (W^{(l)})^T \boldsymbol{\delta}^{(l)}\]
where \(\boldsymbol{\delta}^{(l)} = \frac{\partial \mathcal{L}}{\partial \mathbf{s}^{(l)}}\)
Dimension verification:
Forward (layer \(l\)): \[\mathbf{s}^{(l)} = W^{(l)}\mathbf{a}^{(l-1)} + \mathbf{b}^{(l)}\] \[[n_l \times 1] = [n_l \times n_{l-1}][n_{l-1} \times 1] + [n_l \times 1]\]
Backward: \[\frac{\partial \mathcal{L}}{\partial \mathbf{a}^{(l-1)}} = (W^{(l)})^T \boldsymbol{\delta}^{(l)}\] \[[n_{l-1} \times 1] = [n_{l-1} \times n_l][n_l \times 1]\]
Example: Layer 2 → Layer 1
\(W^{(2)} \in \mathbb{R}^{2 \times 4}\), \(\boldsymbol{\delta}^{(2)} \in \mathbb{R}^{2}\)
\[\frac{\partial \mathcal{L}}{\partial \mathbf{a}^{(1)}} = (W^{(2)})^T \boldsymbol{\delta}^{(2)}\] \[[4 \times 1] = [4 \times 2][2 \times 1]\]
Transpose ensures dimension compatibility
Vector Calculus Notation
Denominator convention (used here):
For \(\mathbf{y} = f(\mathbf{x})\) where \(\mathbf{x} \in \mathbb{R}^n, \mathbf{y} \in \mathbb{R}^m\):
Jacobian matrix: \[\frac{\partial \mathbf{y}}{\partial \mathbf{x}} = \begin{bmatrix} \frac{\partial y_1}{\partial x_1} & \cdots & \frac{\partial y_1}{\partial x_n}\\ \vdots & \ddots & \vdots\\ \frac{\partial y_m}{\partial x_1} & \cdots & \frac{\partial y_m}{\partial x_n} \end{bmatrix} \in \mathbb{R}^{m \times n}\]
Chain rule (left-handed):
For \(\mathcal{L} = g(f(\mathbf{x}))\): \[\nabla_\mathbf{x} \mathcal{L} = \left(\frac{\partial \mathbf{y}}{\partial \mathbf{x}}\right)^T \nabla_\mathbf{y} \mathcal{L}\]
Transpose appears naturally
Numerator convention (alternative):
Jacobian: \[\frac{\partial \mathbf{y}}{\partial \mathbf{x}^T} = \begin{bmatrix} \frac{\partial y_1}{\partial x_1} & \cdots & \frac{\partial y_m}{\partial x_1}\\ \vdots & \ddots & \vdots\\ \frac{\partial y_1}{\partial x_n} & \cdots & \frac{\partial y_m}{\partial x_n} \end{bmatrix} \in \mathbb{R}^{n \times m}\]
Chain rule (right-handed): \[\nabla_\mathbf{x}^T \mathcal{L} = \nabla_\mathbf{y}^T \mathcal{L} \cdot \frac{\partial \mathbf{y}}{\partial \mathbf{x}^T}\]
Both conventions are bookkeeping for chain rule
See: Matrix Calculus (Wikipedia)
Denominator convention more common in optimization
Element-Wise Operations
Hadamard product (element-wise multiply): \(\odot\)
\[\mathbf{a} \odot \mathbf{b} = \begin{bmatrix} a_1 b_1 \\ a_2 b_2 \\ \vdots \\ a_n b_n \end{bmatrix}\]
Example:
\[\begin{bmatrix} 2 \\ 3 \\ -1 \end{bmatrix} \odot \begin{bmatrix} 0.5 \\ 0.2 \\ 0.8 \end{bmatrix} = \begin{bmatrix} 1.0 \\ 0.6 \\ -0.8 \end{bmatrix}\]
Connection to diagonal matrix:
\[\text{diag}(\mathbf{a} \odot \mathbf{b}) = \text{diag}(\mathbf{a}) \text{diag}(\mathbf{b})\]
\[\mathbf{a} \odot \mathbf{b} = \text{diag}(\mathbf{a}) \mathbf{b} = \text{diag}(\mathbf{b}) \mathbf{a}\]
where \(\text{diag}(\mathbf{a})\) puts vector on diagonal:
\[\text{diag}([a_1, a_2, a_3]^T) = \begin{bmatrix} a_1 & 0 & 0 \\ 0 & a_2 & 0 \\ 0 & 0 & a_3 \end{bmatrix}\]
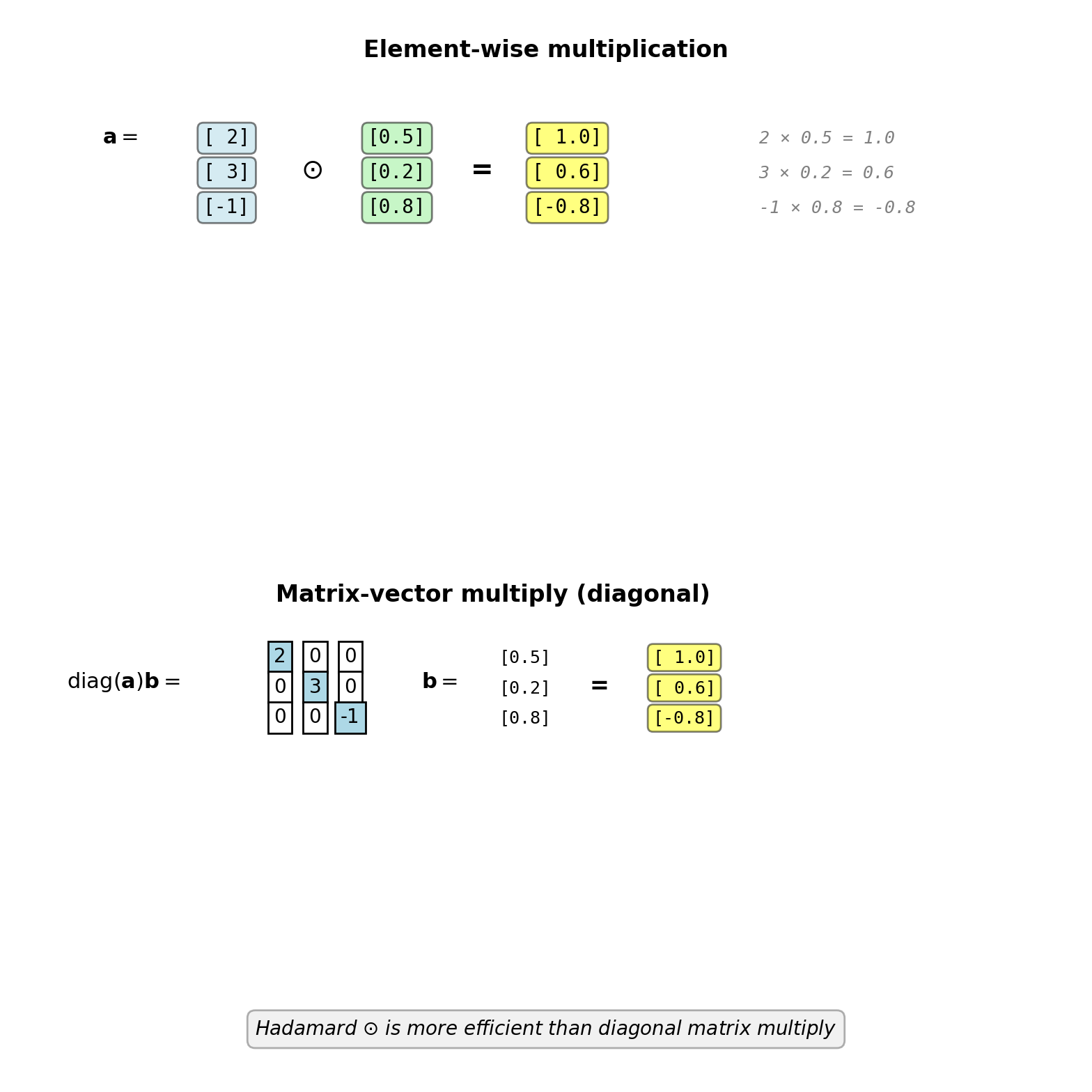
Used in backprop to apply element-wise activation derivatives
Vector Delta Method
Define: \(\boldsymbol{\delta}^{(l)} = \frac{\partial \mathcal{L}}{\partial \mathbf{s}^{(l)}} \in \mathbb{R}^{n_l}\)
Vector of error signals at layer \(l\)
Output layer (softmax + cross-entropy):
For \(\mathbf{y}\) one-hot and \(\mathcal{L} = -\log(a_k^{(L)})\) where \(y_k = 1\):
\[\boldsymbol{\delta}^{(L)} = \mathbf{a}^{(L)} - \mathbf{y}\]
Hidden layers:
\[\boldsymbol{\delta}^{(l)} = (W^{(l+1)})^T \boldsymbol{\delta}^{(l+1)} \odot \sigma'(\mathbf{s}^{(l)})\]
where \(\odot\) is Hadamard (element-wise) product
Convenient since element-wise activation has diagonal Jacobian (zero off-diagonal)
Dimension check:
\[[n_l \times 1] = [n_l \times n_{l+1}][n_{l+1} \times 1] \odot [n_l \times 1]\]
Matrix-vector multiply, then element-wise multiply
Example: 2-layer network
Output delta (\(n_2 = 2\)): \[\boldsymbol{\delta}^{(2)} = \begin{bmatrix} 0.509 \\ -0.509 \end{bmatrix}\]
(from \(\mathbf{a}^{(2)} - \mathbf{y}\) with \(\mathbf{y} = [0, 1]^T\))
Hidden delta (\(n_1 = 4\)):
\[(W^{(2)})^T \boldsymbol{\delta}^{(2)} = \begin{bmatrix} 0.5 & -0.2 \\ -0.3 & 0.4 \\ 0.2 & -0.1 \\ 0.1 & 0.3 \end{bmatrix} \begin{bmatrix} 0.509 \\ -0.509 \end{bmatrix} = \begin{bmatrix} 0.357 \\ 0.051 \\ 0.153 \\ -0.102 \end{bmatrix}\]
\[\sigma'(\mathbf{s}^{(1)}) = \mathbf{a}^{(1)} \odot (1 - \mathbf{a}^{(1)}) = \begin{bmatrix} 0.246 \\ 0.250 \\ 0.250 \\ 0.232 \end{bmatrix}\]
\[\boldsymbol{\delta}^{(1)} = \begin{bmatrix} 0.357 \\ 0.051 \\ 0.153 \\ -0.102 \end{bmatrix} \odot \begin{bmatrix} 0.246 \\ 0.250 \\ 0.250 \\ 0.232 \end{bmatrix} = \begin{bmatrix} 0.088 \\ 0.013 \\ 0.038 \\ -0.024 \end{bmatrix}\]
Backpropagation Flow: Vector Network
Delta propagates backward, weight gradients computed via outer products
Weight Gradient as Outer Product
Scalar to matrix derivation:
Layer computation: \(s_i^{(l)} = \sum_{j=1}^{n_{l-1}} w_{ij}^{(l)} a_j^{(l-1)} + b_i^{(l)}\)
Chain rule: \[\frac{\partial \mathcal{L}}{\partial w_{ij}^{(l)}} = \frac{\partial \mathcal{L}}{\partial s_i^{(l)}} \cdot \frac{\partial s_i^{(l)}}{\partial w_{ij}^{(l)}} = \delta_i^{(l)} \cdot a_j^{(l-1)}\]
Matrix form (all elements): \[\left[\frac{\partial \mathcal{L}}{\partial W^{(l)}}\right]_{ij} = \delta_i^{(l)} \cdot a_j^{(l-1)}\]
Recognize outer product:
\[\frac{\partial \mathcal{L}}{\partial W^{(l)}} = \boldsymbol{\delta}^{(l)} (\mathbf{a}^{(l-1)})^T\]
Dimensions: \([n_l \times 1][1 \times n_{l-1}] = [n_l \times n_{l-1}]\) ✓
Bias gradient:
\[\frac{\partial \mathcal{L}}{\partial \mathbf{b}^{(l)}} = \boldsymbol{\delta}^{(l)}\]
Complete 2-Layer Example
Setup:
x = np.array([1.0, 0.5, -0.5])
y = np.array([0, 1]) # one-hot
W1 = np.array([[0.1, 0.2, -0.1],
[0.3, -0.2, 0.1],
[-0.1, 0.1, 0.2],
[0.2, 0.3, -0.3]])
b1 = np.array([0.1, -0.1, 0.0, 0.2])
W2 = np.array([[0.5, -0.3, 0.2, 0.1],
[-0.2, 0.4, -0.1, 0.3]])
b2 = np.array([0.0, 0.1])Forward:
\[\mathbf{s}^{(1)} = \begin{bmatrix} 0.25 \\ 0.05 \\ -0.05 \\ 0.55 \end{bmatrix}, \quad \mathbf{a}^{(1)} = \begin{bmatrix} 0.562 \\ 0.513 \\ 0.488 \\ 0.634 \end{bmatrix}\]
\[\mathbf{s}^{(2)} = \begin{bmatrix} 0.421 \\ 0.384 \end{bmatrix}, \quad \mathbf{a}^{(2)} = \begin{bmatrix} 0.509 \\ 0.491 \end{bmatrix}\]
Loss: \(\mathcal{L} = -\log(0.491) = 0.711\)
Backward:
\[\boldsymbol{\delta}^{(2)} = \begin{bmatrix} 0.509 \\ -0.509 \end{bmatrix}\]
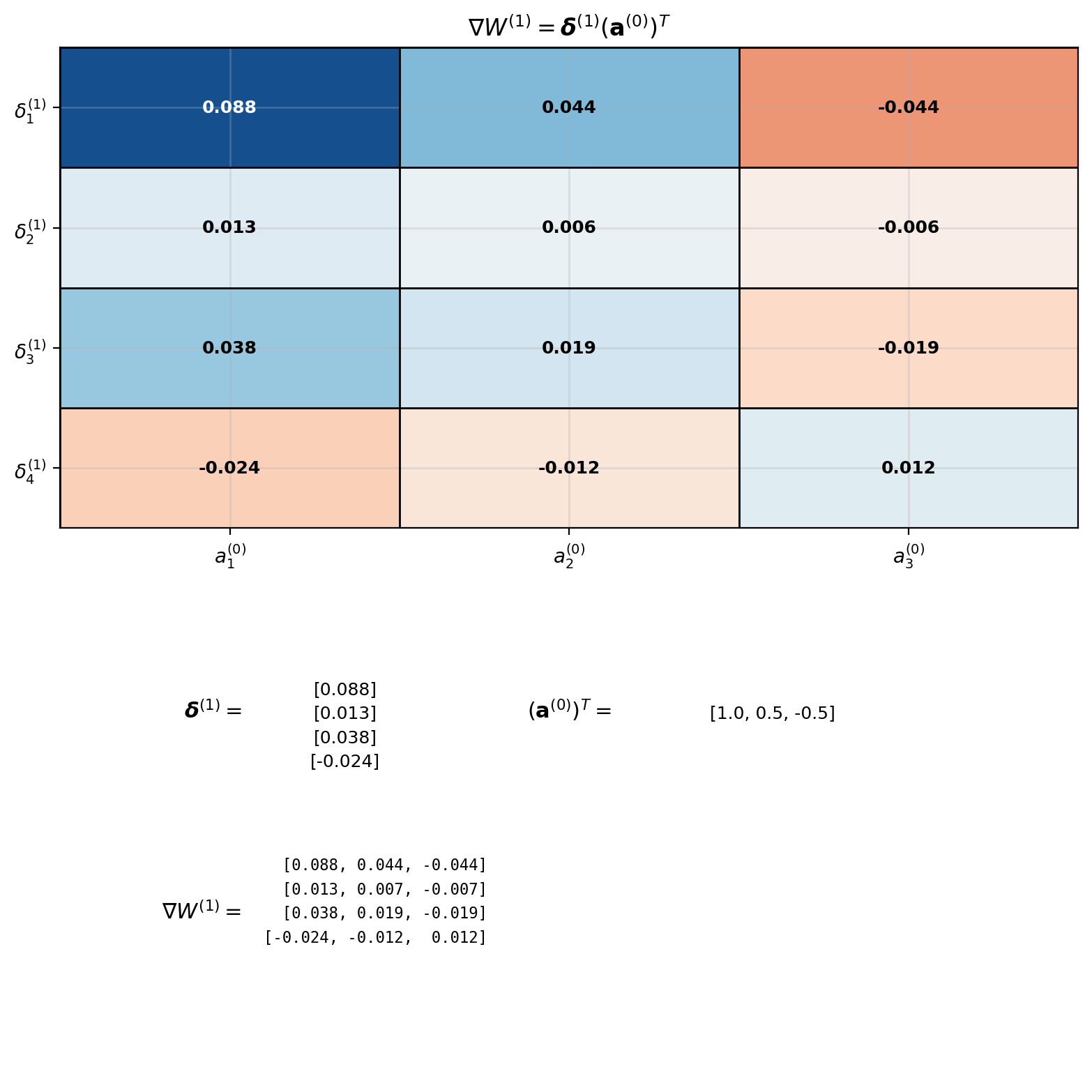
\[\boldsymbol{\delta}^{(1)} = (W^{(2)})^T \boldsymbol{\delta}^{(2)} \odot \sigma'(\mathbf{s}^{(1)})\] \[= \begin{bmatrix} 0.357 \\ 0.051 \\ 0.153 \\ -0.102 \end{bmatrix} \odot \begin{bmatrix} 0.246 \\ 0.250 \\ 0.250 \\ 0.232 \end{bmatrix} = \begin{bmatrix} 0.088 \\ 0.013 \\ 0.038 \\ -0.024 \end{bmatrix}\]
Gradients:
\[\nabla W^{(2)} = \begin{bmatrix} 0.509 \\ -0.509 \end{bmatrix} \begin{bmatrix} 0.562 & 0.513 & 0.488 & 0.634 \end{bmatrix}\] \[= \begin{bmatrix} 0.286 & 0.261 & 0.248 & 0.323 \\ -0.286 & -0.261 & -0.248 & -0.323 \end{bmatrix}\]
\[\nabla W^{(1)} = \begin{bmatrix} 0.088 \\ 0.013 \\ 0.038 \\ -0.024 \end{bmatrix} \begin{bmatrix} 1.0 & 0.5 & -0.5 \end{bmatrix}\] \[= \begin{bmatrix} 0.088 & 0.044 & -0.044 \\ 0.013 & 0.007 & -0.007 \\ 0.038 & 0.019 & -0.019 \\ -0.024 & -0.012 & 0.012 \end{bmatrix}\]
Gradient Verification
Finite difference check:
For parameter \(w_{ij}\): \[\frac{\partial \mathcal{L}}{\partial w_{ij}} \approx \frac{\mathcal{L}(w_{ij} + \epsilon) - \mathcal{L}(w_{ij} - \epsilon)}{2\epsilon}\]
Check \(W^{(2)}_{11}\) (row 1, column 1):
Analytical: \(\nabla W^{(2)}_{11} = 0.286\)
Numerical with \(\epsilon = 10^{-5}\):
Original \(W^{(2)}_{11} = 0.5\)
\(\mathcal{L}(W^{(2)}_{11} = 0.50001) = 0.711003\)
\(\mathcal{L}(W^{(2)}_{11} = 0.49999) = 0.710997\)
\[\frac{0.711003 - 0.710997}{0.00002} = 0.286\]
Analytical and numerical match
Batch Processing
Single sample: \(\mathbf{x} \in \mathbb{R}^d\)
\[\mathbf{s} = W\mathbf{x} + \mathbf{b}\]
Batch of \(m\) samples: \(X \in \mathbb{R}^{m \times d}\)
Samples as rows: \[X = \begin{bmatrix} — \mathbf{x}_1^T — \\ — \mathbf{x}_2^T — \\ \vdots \\ — \mathbf{x}_m^T — \end{bmatrix}\]
Forward pass (layer \(l\)):
\[S^{(l)} = A^{(l-1)} (W^{(l)})^T + \mathbf{1}_m (\mathbf{b}^{(l)})^T\]
where \(A^{(l-1)} \in \mathbb{R}^{m \times n_{l-1}}\)
Bias broadcast: add \(\mathbf{b}^{(l)}\) to each row
Activation: Element-wise on matrix
\[A^{(l)} = \sigma(S^{(l)})\]
Dimension check:
\[S^{(l)}: [m \times n_l] = [m \times n_{l-1}][n_{l-1} \times n_l] + [m \times n_l]\]
Backward pass:
Delta for batch: \(\Delta^{(l)} \in \mathbb{R}^{m \times n_l}\)
Each row is delta for one sample
Weight gradient (average over batch):
\[\nabla W^{(l)} = \frac{1}{m} (\Delta^{(l)})^T A^{(l-1)}\]
\[[n_l \times n_{l-1}] = \frac{1}{m} [n_l \times m][m \times n_{l-1}]\]
Bias gradient:
\[\nabla \mathbf{b}^{(l)} = \frac{1}{m} \mathbf{1}_m^T \Delta^{(l)}\]
\[[n_l \times 1] = \frac{1}{m} [1 \times m][m \times n_l]\]
Sum deltas across batch, average
Batch Processing: Accumulation
For each sample \(i = 1, \ldots, m\) in batch:
Forward pass: \[\mathbf{a}_i^{(l)} = \sigma(W^{(l)}\mathbf{a}_i^{(l-1)} + \mathbf{b}^{(l)})\]
Backward pass: \[\boldsymbol{\delta}_i^{(l)} = (W^{(l+1)})^T \boldsymbol{\delta}_i^{(l+1)} \odot \sigma'(\mathbf{z}_i^{(l)})\]
Accumulate gradients: \[\nabla W^{(l)} = \frac{1}{m} \sum_{i=1}^m \boldsymbol{\delta}_i^{(l)} (\mathbf{a}_i^{(l-1)})^T\]
\[\nabla \mathbf{b}^{(l)} = \frac{1}{m} \sum_{i=1}^m \boldsymbol{\delta}_i^{(l)}\]
Single SGD update after processing batch:
\[W^{(l)} \leftarrow W^{(l)} - \eta \nabla W^{(l)}\] \[\mathbf{b}^{(l)} \leftarrow \mathbf{b}^{(l)} - \eta \nabla \mathbf{b}^{(l)}\]
Matrix form (all samples stacked):
\[\nabla W^{(l)} = \frac{1}{m} \Delta^{(l)T} A^{(l-1)}\]
where \(\Delta^{(l)} \in \mathbb{R}^{m \times n_l}\) stacks all \(\boldsymbol{\delta}_i^{(l)}\) as rows
Same result, different notation
Batch Computation Example
Batch of 3 samples:
\[X = \begin{bmatrix} 1.0 & 0.5 & -0.5 \\ 0.8 & -0.3 & 0.4 \\ -0.6 & 0.7 & 0.2 \end{bmatrix} \in \mathbb{R}^{3 \times 3}\]
\[Y = \begin{bmatrix} 0 & 1 \\ 1 & 0 \\ 0 & 1 \end{bmatrix} \in \mathbb{R}^{3 \times 2}\]
Forward (Layer 1, \(W^{(1)} \in \mathbb{R}^{4 \times 3}\)):
\[S^{(1)} = X (W^{(1)})^T + \mathbf{1}_3 (\mathbf{b}^{(1)})^T\]
\[[3 \times 4] = [3 \times 3][3 \times 4] + [3 \times 4]\]
\[S^{(1)} = \begin{bmatrix} 0.25 & 0.05 & -0.05 & 0.55 \\ 0.23 & 0.14 & -0.02 & 0.41 \\ -0.11 & -0.07 & 0.15 & 0.08 \end{bmatrix}\]
\[A^{(1)} = \sigma(S^{(1)})\]
Backward:
Output delta (3 samples × 2 classes): \[\Delta^{(2)} = A^{(2)} - Y = \begin{bmatrix} 0.509 & -0.509 \\ -0.492 & 0.492 \\ 0.503 & -0.503 \end{bmatrix}\]
Weight gradient:
\[\nabla W^{(2)} = \frac{1}{3} (\Delta^{(2)})^T A^{(1)}\]
\[[2 \times 4] = \frac{1}{3} [2 \times 3][3 \times 4]\]
Average gradient across 3 samples
Why batch:
- GPU matrix multiply: \(O(mn_ln_{l-1})\) for batch
- 3 separate forwards: \(3 \times O(n_ln_{l-1})\)
- Same asymptotic cost, but batching uses optimized BLAS
- Memory access patterns favor contiguous batch data
General Backpropagation Algorithm
Backpropagation Algorithm
Input: Network \(\{W^{(l)}, \mathbf{b}^{(l)}\}_{l=1}^L\), data \((\mathbf{x}, \mathbf{y})\)
Output: Gradients \(\{\nabla W^{(l)}, \nabla \mathbf{b}^{(l)}\}_{l=1}^L\)
Forward pass:
a^(0) ← x
for l = 1 to L:
s^(l) ← W^(l) a^(l-1) + b^(l)
a^(l) ← σ^(l)(s^(l))
store: a^(l-1), s^(l), a^(l)Backward pass:
δ^(L) ← ∇_a^(L) L(a^(L), y)
for l = L down to 1:
δ^(l) ← (W^(l+1))^T δ^(l+1) ⊙ σ'(s^(l))Gradient computation:
for l = 1 to L:
∇W^(l) ← δ^(l) (a^(l-1))^T
∇b^(l) ← δ^(l)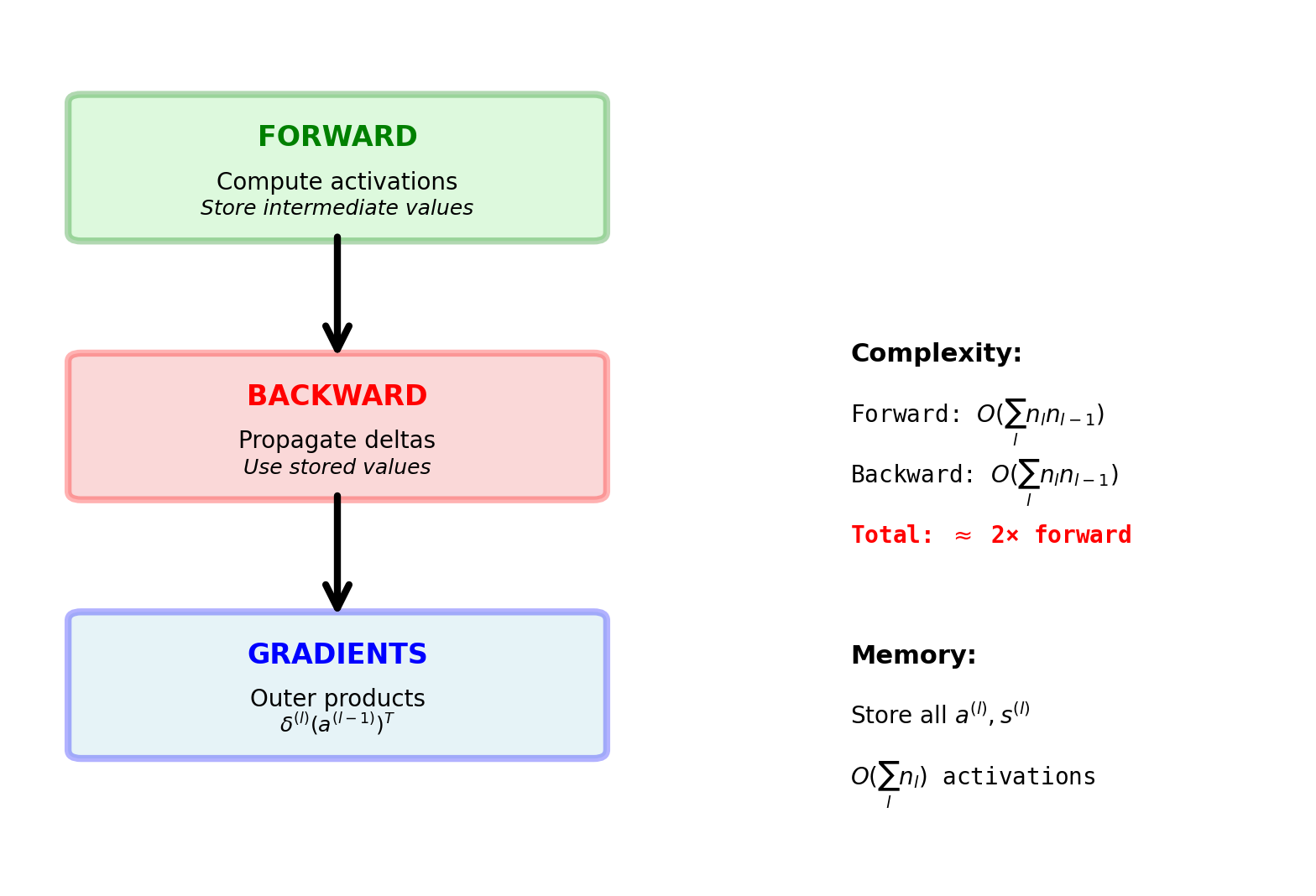
Single forward pass + single backward pass computes all gradients
Why “Backpropagation”?
Historical context:
Rumelhart, Hinton, Williams (1986) paper: “Learning representations by back-propagating errors”
Algorithm existed earlier (Werbos 1974, others) but 1986 paper demonstrated effectiveness for neural networks
Name origin:
Gradients propagate backward through network:
- Compute loss at output
- Gradient flows from loss back to earlier layers
- Each layer receives gradient from layer ahead
- Apply chain rule locally
- Pass gradient to layer behind
Direction: Output \(\to\) Input (opposite of data flow)
Data flow:
Forward: \(\mathbf{x} \to \mathbf{a}^{(1)} \to \mathbf{a}^{(2)} \to \cdots \to \mathbf{a}^{(L)} \to \mathcal{L}\)
Backward: \(\nabla_{\mathbf{x}} \mathcal{L} \leftarrow \boldsymbol{\delta}^{(1)} \leftarrow \boldsymbol{\delta}^{(2)} \leftarrow \cdots \leftarrow \boldsymbol{\delta}^{(L)} \leftarrow 1\)
Gradients propagate in reverse order (output \(\to\) input)
Common misconception: “Backpropagation of errors”
Correct: Backpropagation of gradients
Delta values \(\boldsymbol{\delta}^{(l)}\) are not errors—they are partial derivatives \(\frac{\partial \mathcal{L}}{\partial \mathbf{s}^{(l)}}\)
Computational Complexity Analysis
Forward pass (single sample):
Layer \(l\): Matrix multiply \(W^{(l)}\mathbf{a}^{(l-1)}\)
Cost: \(O(n_l \cdot n_{l-1})\) multiplications
Activation: \(O(n_l)\) (element-wise)
Total forward: \(\sum_{l=1}^L O(n_l \cdot n_{l-1})\)
Backward pass:
Delta propagation: \((W^{(l+1)})^T \boldsymbol{\delta}^{(l+1)}\)
Cost: \(O(n_l \cdot n_{l+1})\) (same as forward)
Weight gradient: \(\boldsymbol{\delta}^{(l)} (\mathbf{a}^{(l-1)})^T\)
Cost: \(O(n_l \cdot n_{l-1})\) (outer product)
Total backward: \(2 \times \sum_{l=1}^L O(n_l \cdot n_{l-1})\)
Result: Backward cost = 2× Forward cost
(Delta propagation + Weight gradients)
Total training step: Forward + Backward = 3× forward pass
Example: 3-layer network
\(784 \to 256 \to 128 \to 10\)
Forward operations:
- Layer 1: \(784 \times 256 = 200{,}704\)
- Layer 2: \(256 \times 128 = 32{,}768\)
- Layer 3: \(128 \times 10 = 1{,}280\)
- Total: \(234{,}752\) multiplications
Backward operations:
- Delta 3→2: \(128 \times 10 = 1{,}280\)
- Delta 2→1: \(256 \times 128 = 32{,}768\)
- Delta 1→0: \(784 \times 256 = 200{,}704\)
- Gradients: Same counts as forward
- Total: \(2 \times 234{,}752 = 469{,}504\)
Total: \(3 \times\) forward pass operations
Compare to numerical differentiation: \(234{,}752\) forward passes
Speedup: \(\frac{234{,}752}{3} \approx 78{,}000\times\)
Memory Requirements
Parameters: \(\sum_{l=1}^L n_l \cdot n_{l-1}\)
Must store \(W^{(l)}\) and \(\mathbf{b}^{(l)}\) for all layers
Gradients: Same size as parameters
Store \(\nabla W^{(l)}\) and \(\nabla \mathbf{b}^{(l)}\)
Activations: \(\sum_{l=1}^L n_l \cdot m\)
Store \(\mathbf{a}^{(l)}\) and \(\mathbf{s}^{(l)}\) for batch size \(m\)
Needed for backward pass
Memory scaling:
Parameters: Fixed (independent of batch size)
Activations: Linear in batch size
Activations dominate for large batches
Example: ResNet-50, batch 32, ImageNet (224×224 input)
Parameters:
- \(W^{(l)}\), \(\mathbf{b}^{(l)}\): 25M parameters
- Storage: \(25 \times 10^6 \times 4\) bytes = 100 MB
Gradients:
- \(\nabla W^{(l)}\), \(\nabla \mathbf{b}^{(l)}\): 25M values
- Storage: 100 MB
Activations (batch 32):
Activation memory varies by layer (spatial dimensions decrease, channels increase):
- Early layers: \(56 \times 56 \times 256 \times 32 \times 4\) bytes ≈ 65 MB
- Middle layers: \(28 \times 28 \times 512 \times 32 \times 4\) bytes ≈ 33 MB
- Deep layers: \(14 \times 14 \times 1024 \times 32 \times 4\) bytes ≈ 26 MB
Forward activations: ~200 MB, Backward gradients: ~200 MB
Total memory (batch 32): 100 + 100 + 400 = 600 MB
Scaling with batch size:
- Batch 64: Activations ≈ 800 MB, total ≈ 1000 MB
- Batch 128: Activations ≈ 1600 MB, total ≈ 1800 MB
- Batch 256: Activations ≈ 3200 MB, total ≈ 3400 MB
For large batches, activations dominate memory usage
Activation Function Derivatives
Algorithm unchanged—only \(\sigma'(\mathbf{s}^{(l)})\) differs per layer
Sigmoid: \(\sigma(s) = \frac{1}{1+e^{-s}}\)
\[\sigma'(s) = \sigma(s)(1-\sigma(s))\]
Can compute from stored activation: \(a(1-a)\)
Tanh: \(\sigma(s) = \tanh(s)\)
\[\tanh'(s) = 1 - \tanh^2(s)\]
Also from activation: \(1 - a^2\)
ReLU: \(\sigma(s) = \max(0, s)\)
\[\text{ReLU}'(s) = \begin{cases} 1 & s > 0 \\ 0 & s \leq 0 \end{cases}\]
Indicator function (discontinuous at 0)
Leaky ReLU: \(\sigma(s) = \max(\alpha s, s)\) with \(\alpha = 0.01\)
\[\text{LReLU}'(s) = \begin{cases} 1 & s > 0 \\ \alpha & s \leq 0 \end{cases}\]
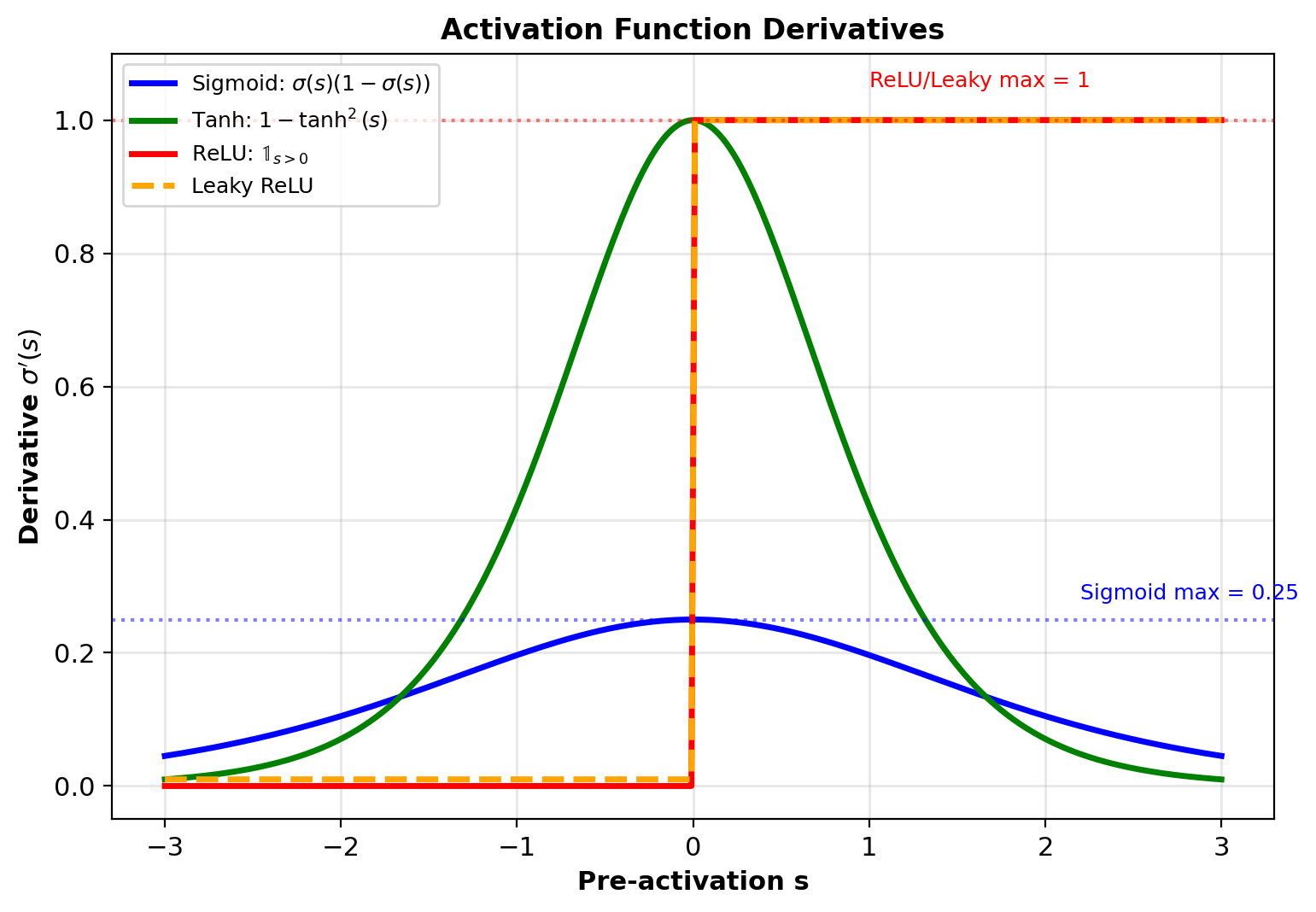
ReLU advantages:
- Sparse gradients (50% zeros)
- No vanishing gradient for active units (\(s > 0\))
- Cheap to compute
Non-Element-Wise Activations
Element-wise activations (sigmoid, tanh, ReLU):
\[a_i^{(l)} = h(s_i^{(l)})\]
Each output depends only on corresponding input
Jacobian is diagonal: \[\frac{\partial a_i^{(l)}}{\partial s_j^{(l)}} = \begin{cases} h'(s_i^{(l)}) & i = j \\ 0 & i \neq j \end{cases}\]
Delta update uses Hadamard product: \[\boldsymbol{\delta}^{(l)} = (W^{(l+1)})^T \boldsymbol{\delta}^{(l+1)} \odot \sigma'(\mathbf{s}^{(l)})\]
Softmax (non-element-wise):
\[a_i = \frac{e^{s_i}}{\sum_j e^{s_j}}\]
Each output depends on all inputs
Jacobian is full matrix: \[\frac{\partial a_i}{\partial s_j} = \begin{cases} a_i(1 - a_i) & i = j \\ -a_i a_j & i \neq j \end{cases}\]
Delta initialization requires matrix-vector product: \[\boldsymbol{\delta}^{(L)} = \nabla_{\mathbf{s}^{(L)}} h(\mathbf{s}^{(L)}) \cdot \nabla_{\mathbf{a}^{(L)}} \mathcal{L}\]
Special case (softmax + cross-entropy): \[\boldsymbol{\delta}^{(L)} = \mathbf{a}^{(L)} - \mathbf{y}\]
Jacobian multiplication simplifies to subtraction
Backpropagation with Regularization
Standard
Regularized
Objective: \[\min_W \mathcal{L} = \min_W \frac{1}{m}\sum_{i=1}^m \ell(\hat{\mathbf{y}}^{(i)}, \mathbf{y}^{(i)})\]
Gradient: \[\nabla W^{(l)} = \boldsymbol{\delta}^{(l)}(\mathbf{a}^{(l-1)})^T\]
Objective: \[\min_W \mathcal{L}_{\text{reg}} = \frac{1}{m}\sum_{i=1}^m \ell(\hat{\mathbf{y}}^{(i)}, \mathbf{y}^{(i)}) + \lambda R(W)\]
Gradient: \[\nabla W^{(l)} = \boldsymbol{\delta}^{(l)}(\mathbf{a}^{(l-1)})^T + \lambda \nabla_W R(W^{(l)})\]
Common regularizers: \(R_{L2}(W) = \|W\|_2\), \(R_{L1}(W) = \|W\|_1\)
What remains unchanged:
- Forward pass computation
- Delta recursion: \(\boldsymbol{\delta}^{(l)} = (W^{(l+1)})^T \boldsymbol{\delta}^{(l+1)} \odot \sigma'(\mathbf{s}^{(l)})\)
- Bias gradients: \(\nabla \mathbf{b}^{(l)} = \boldsymbol{\delta}^{(l)}\) (biases not regularized)
Why: Regularization term \(R(W)\) depends only on weights, not activations or biases
Regularization Effects
L2 regularization (weight decay):
\[\mathcal{L}_{\text{total}} = \mathcal{L} + \lambda \sum_l \|W^{(l)}\|_F^2\]
Frobenius norm: \(\|W\|_F^2 = \sum_{i,j} w_{ij}^2\)
Gradient: \[\frac{\partial \mathcal{L}_{\text{total}}}{\partial W^{(l)}} = \frac{\partial \mathcal{L}}{\partial W^{(l)}} + 2\lambda W^{(l)}\]
Modified update: \[W^{(l)} \leftarrow W^{(l)} - \eta\left(\boldsymbol{\delta}^{(l)}(\mathbf{a}^{(l-1)})^T + 2\lambda W^{(l)}\right)\]
Equivalent to weight decay: \(W^{(l)} \leftarrow (1 - 2\eta\lambda)W^{(l)} - \eta \boldsymbol{\delta}^{(l)}(\mathbf{a}^{(l-1)})^T\)
L1 regularization:
\[\mathcal{L}_{\text{total}} = \mathcal{L} + \lambda \sum_l \|W^{(l)}\|_1\]
L1 norm: \(\|W\|_1 = \sum_{i,j} |w_{ij}|\)
Subgradient: \[\frac{\partial \mathcal{L}_{\text{total}}}{\partial w_{ij}} = \frac{\partial \mathcal{L}}{\partial w_{ij}} + \lambda \text{sign}(w_{ij})\]
Modified update: \[w_{ij} \leftarrow w_{ij} - \eta\left(\frac{\partial \mathcal{L}}{\partial w_{ij}} + \lambda \text{sign}(w_{ij})\right)\]
Promotes sparsity: weights shrink toward zero
Bias terms typically not regularized
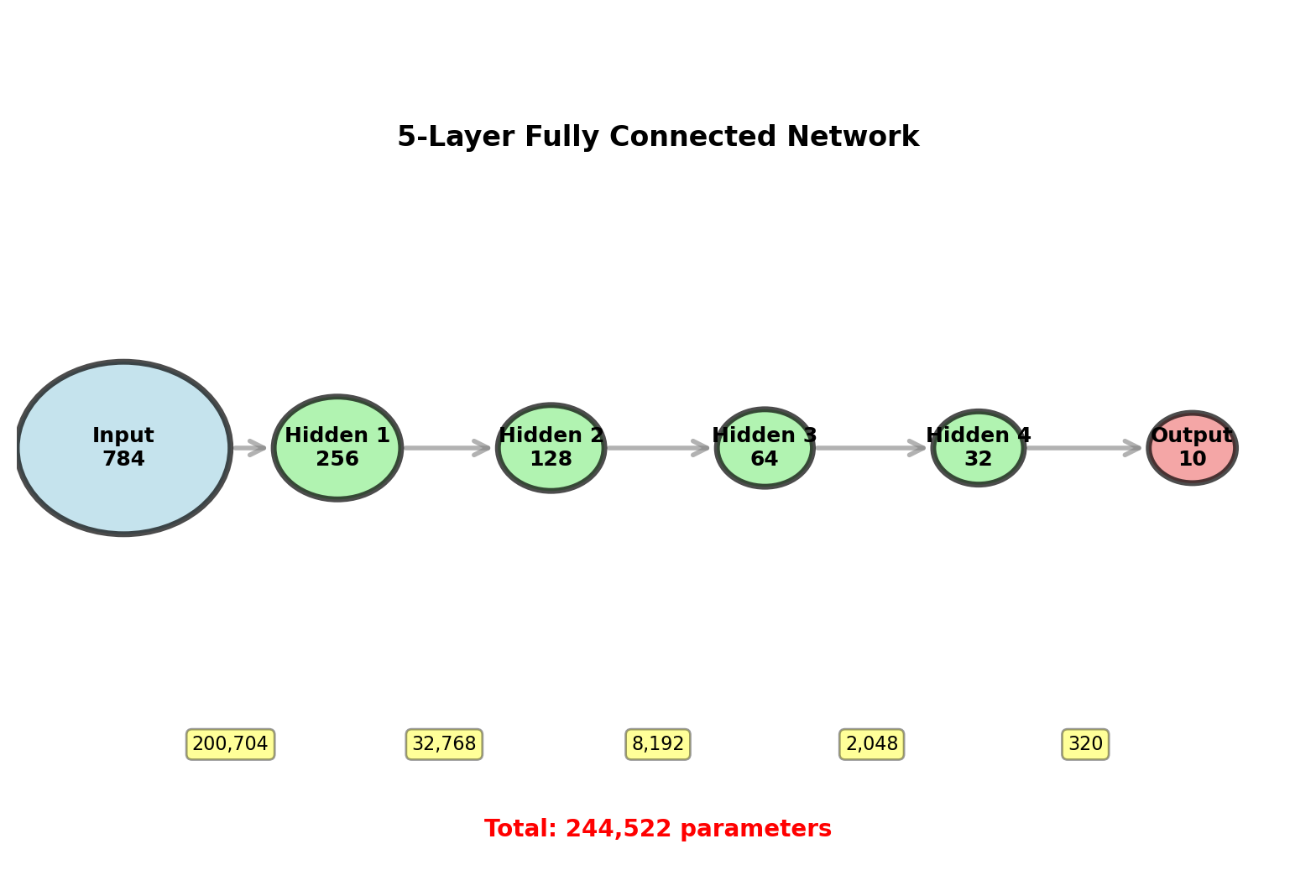
Five-Layer Network Example
Architecture: MNIST digit classifier
\[784 \to 256 \to 128 \to 64 \to 32 \to 10\]
Input: 28×28 grayscale images = 784 pixels
Output: 10 class probabilities
Parameters per layer:
- \(W^{(1)}\): \(256 \times 784 = 200{,}704\)
- \(W^{(2)}\): \(128 \times 256 = 32{,}768\)
- \(W^{(3)}\): \(64 \times 128 = 8{,}192\)
- \(W^{(4)}\): \(32 \times 64 = 2{,}048\)
- \(W^{(5)}\): \(10 \times 32 = 320\)
Biases: \(256 + 128 + 64 + 32 + 10 = 490\)
Total: \(244{,}032\) weights + \(490\) biases = \(244{,}522\) parameters
Backprop computes all 244,522 gradients in 2 passes (1 forward + 1 backward)
Gradient Flow Through Depth
Delta magnitude at layer \(l\):
\[\|\boldsymbol{\delta}^{(l)}\| \approx \|\boldsymbol{\delta}^{(L)}\| \prod_{k=l+1}^L \|W^{(k)}\| \|\sigma'(\mathbf{s}^{(k)})\|\]
Rough approximation ignoring vector structure
Sigmoid network:
Maximum derivative: \(\max_s \sigma'(s) = 0.25\) at \(s=0\)
Typical values: \(\sigma'(s) \approx 0.2\) in practice
After 10 layers: \((0.2)^{10} \approx 10^{-7}\)
Gradients vanish exponentially with depth
Early layers receive near-zero gradients, fail to train
ReLU network:
Derivative: \(\text{ReLU}'(s) \in \{0, 1\}\)
Active units (\(s > 0\)): gradient = 1 (no shrinking)
Dead units (\(s \leq 0\)): gradient = 0 (propagation stops)
Better gradient flow if units stay active
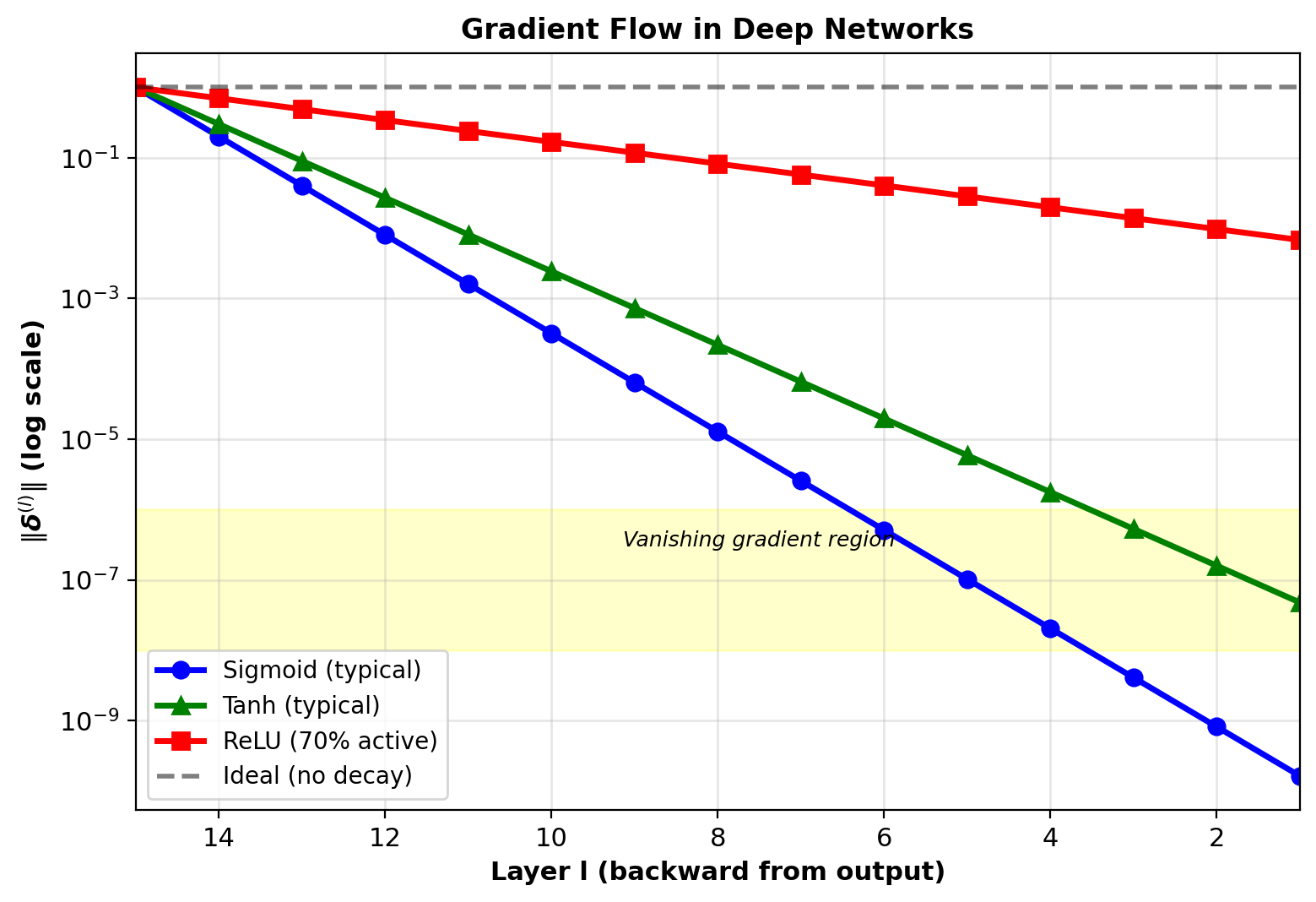
Sigmoid/tanh: Exponential decay
ReLU: Better but still degrades
Computational Graph Framework
Networks as Directed Acyclic Graphs
Nodes: Operations (MatMul, Add, Sigmoid, etc.)
Edges: Tensors flowing between operations
Example: 2-layer network decomposed
Forward: \(\mathbf{x} \to W^{(1)}\mathbf{x} \to + \mathbf{b}^{(1)} \to \sigma \to W^{(2)} \to + \mathbf{b}^{(2)} \to \sigma \to \mathcal{L}\)
Each arrow represents data dependency
Directed: Information flows one direction (forward)
Acyclic: No loops (feedforward network)
Topological order: Can order nodes so all inputs come before outputs
Forward pass: Traverse in topological order
Backward pass: Traverse in reverse topological order
Benefits:
- Modular: Each operation self-contained
- Composable: Build complex functions from primitives
- Automatic: Can differentiate any graph mechanically
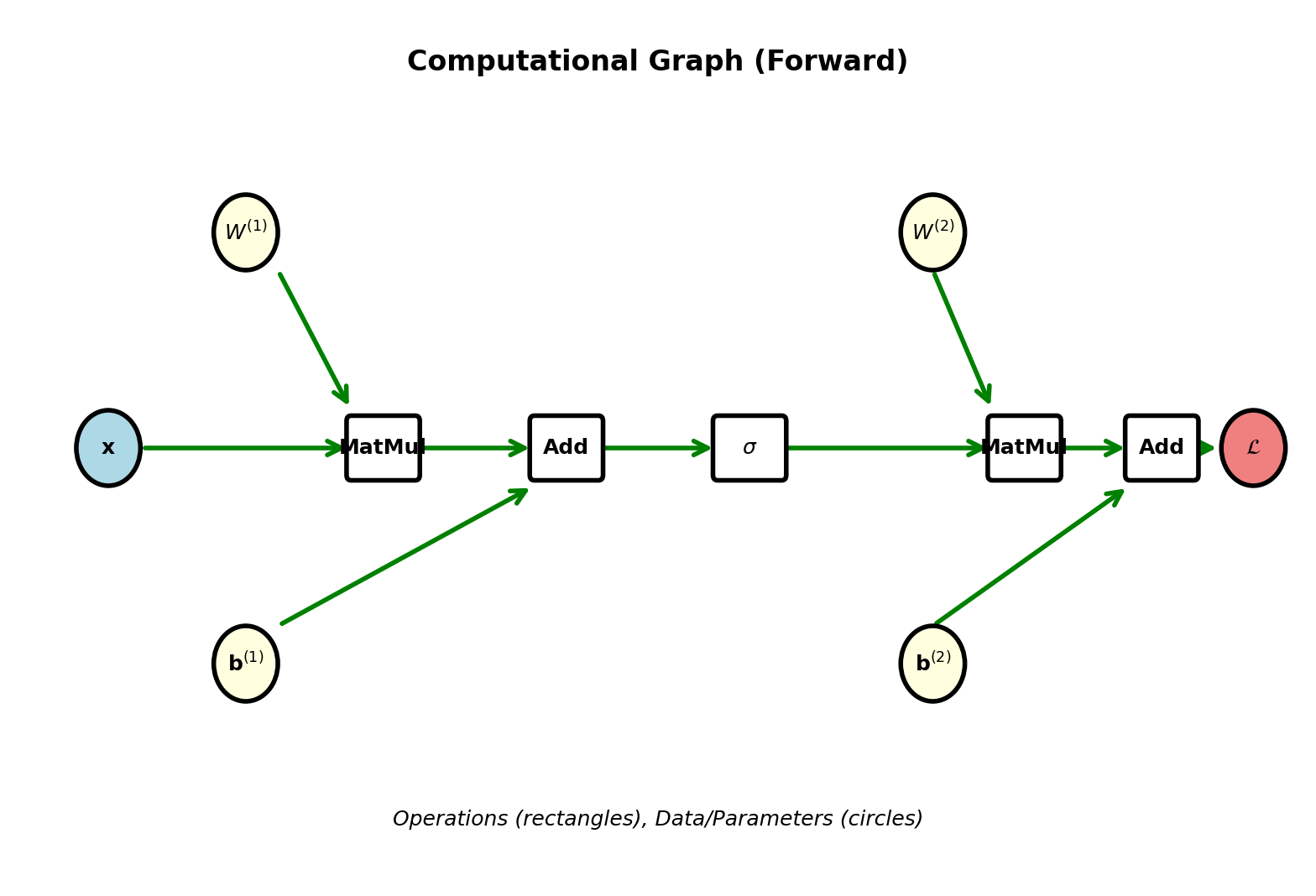
Local Gradient Principle
Each node: Implements forward and backward
class Operation:
def forward(self, inputs):
# Compute output from inputs
# Cache inputs for backward
self.cache = inputs
return self.compute(inputs)
def backward(self, grad_output):
# Compute gradient w.r.t. inputs
# Use cached values
return self.local_gradient(
grad_output, self.cache)No global knowledge required
Node only needs:
- How to compute output from inputs (forward)
- How to compute input gradients from output gradient (backward)
Chain rule automatic:
Graph framework connects local gradients
Node A → Node B: \(\frac{\partial \mathcal{L}}{\partial \text{input}_A} = \frac{\partial \text{output}_B}{\partial \text{input}_A}^T \frac{\partial \mathcal{L}}{\partial \text{output}_B}\)
Framework handles composition
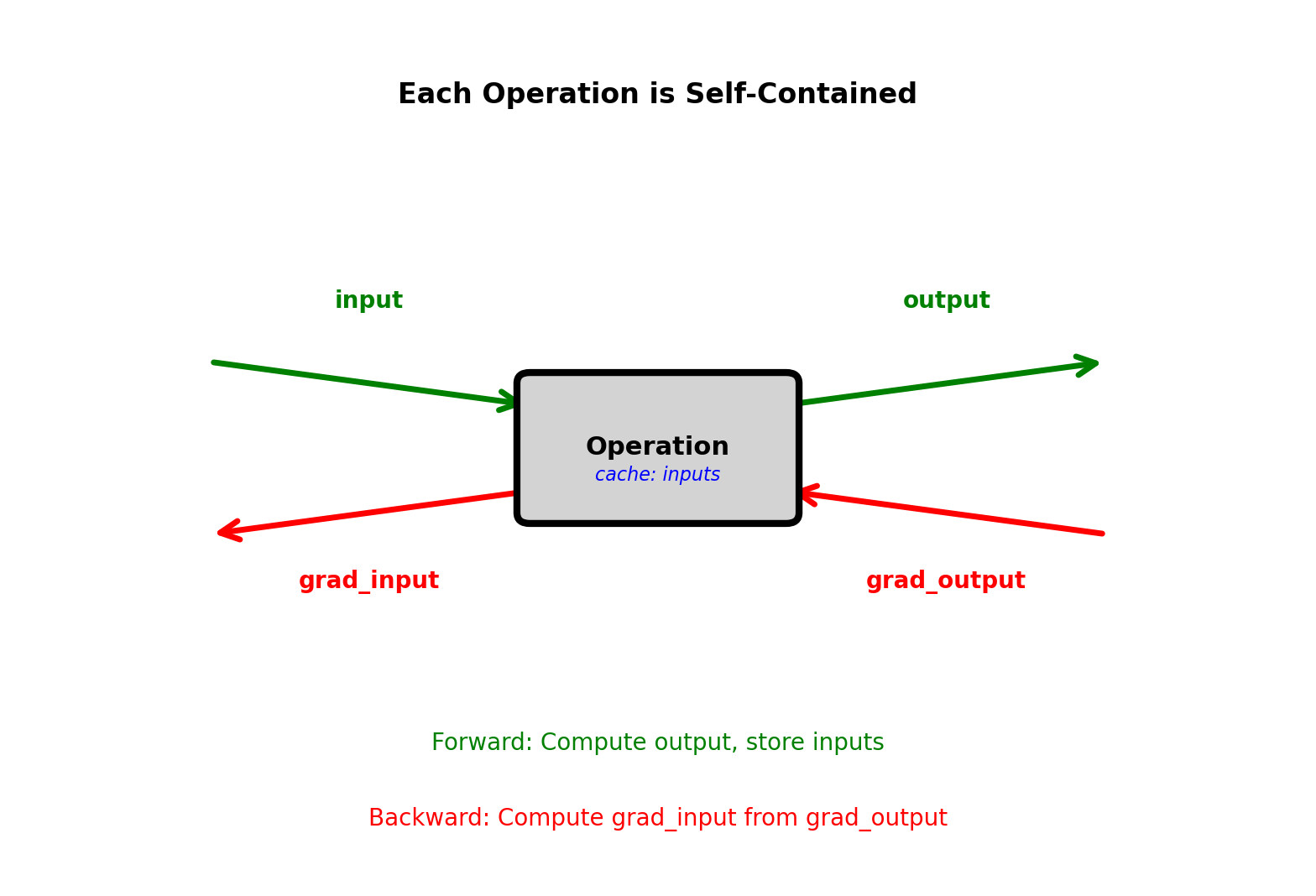
Matrix Multiplication Node
Forward: \(\mathbf{y} = A\mathbf{x}\)
Input: Matrix \(A \in \mathbb{R}^{m \times n}\), vector \(\mathbf{x} \in \mathbb{R}^n\)
Output: \(\mathbf{y} \in \mathbb{R}^m\)
Backward: Given \(\frac{\partial \mathcal{L}}{\partial \mathbf{y}}\), compute gradients w.r.t. inputs
Gradient w.r.t. \(\mathbf{x}\): \[\frac{\partial \mathcal{L}}{\partial \mathbf{x}} = A^T \frac{\partial \mathcal{L}}{\partial \mathbf{y}}\]
Dimension: \([n \times 1] = [n \times m][m \times 1]\)
Gradient w.r.t. \(A\): \[\frac{\partial \mathcal{L}}{\partial A} = \frac{\partial \mathcal{L}}{\partial \mathbf{y}} \mathbf{x}^T\]
Dimension: \([m \times n] = [m \times 1][1 \times n]\)
Implementation:
Numerical example:
\[A = \begin{bmatrix} 0.5 & 0.3 \\ -0.2 & 0.4 \end{bmatrix}, \quad \mathbf{x} = \begin{bmatrix} 1 \\ 2 \end{bmatrix}\]
Forward: \[\mathbf{y} = \begin{bmatrix} 0.5(1) + 0.3(2) \\ -0.2(1) + 0.4(2) \end{bmatrix} = \begin{bmatrix} 1.1 \\ 0.6 \end{bmatrix}\]
Backward (assume \(\frac{\partial \mathcal{L}}{\partial \mathbf{y}} = \begin{bmatrix} 0.8 \\ -0.5 \end{bmatrix}\)):
\[\frac{\partial \mathcal{L}}{\partial \mathbf{x}} = \begin{bmatrix} 0.5 & -0.2 \\ 0.3 & 0.4 \end{bmatrix} \begin{bmatrix} 0.8 \\ -0.5 \end{bmatrix} = \begin{bmatrix} 0.5 \\ 0.04 \end{bmatrix}\]
\[\frac{\partial \mathcal{L}}{\partial A} = \begin{bmatrix} 0.8 \\ -0.5 \end{bmatrix} \begin{bmatrix} 1 & 2 \end{bmatrix} = \begin{bmatrix} 0.8 & 1.6 \\ -0.5 & -1.0 \end{bmatrix}\]

Addition Node
Forward: \(z = x + y\)
Inputs: Scalars, vectors, or matrices (same shape)
Output: Same shape as inputs
Backward: Given \(\frac{\partial \mathcal{L}}{\partial z}\)
Addition distributes gradient to both inputs:
\[\frac{\partial \mathcal{L}}{\partial x} = \frac{\partial \mathcal{L}}{\partial z}\] \[\frac{\partial \mathcal{L}}{\partial y} = \frac{\partial \mathcal{L}}{\partial z}\]
Gradient copies to each input (no modification)
Broadcast addition: \(\mathbf{z} = \mathbf{x} + b\) where \(b\) scalar
Forward: Add \(b\) to each element of \(\mathbf{x}\)
Backward: \[\frac{\partial \mathcal{L}}{\partial \mathbf{x}} = \frac{\partial \mathcal{L}}{\partial \mathbf{z}}\] \[\frac{\partial \mathcal{L}}{\partial b} = \sum_i \frac{\partial \mathcal{L}}{\partial z_i}\]
Gradient w.r.t. scalar sums gradients from all elements
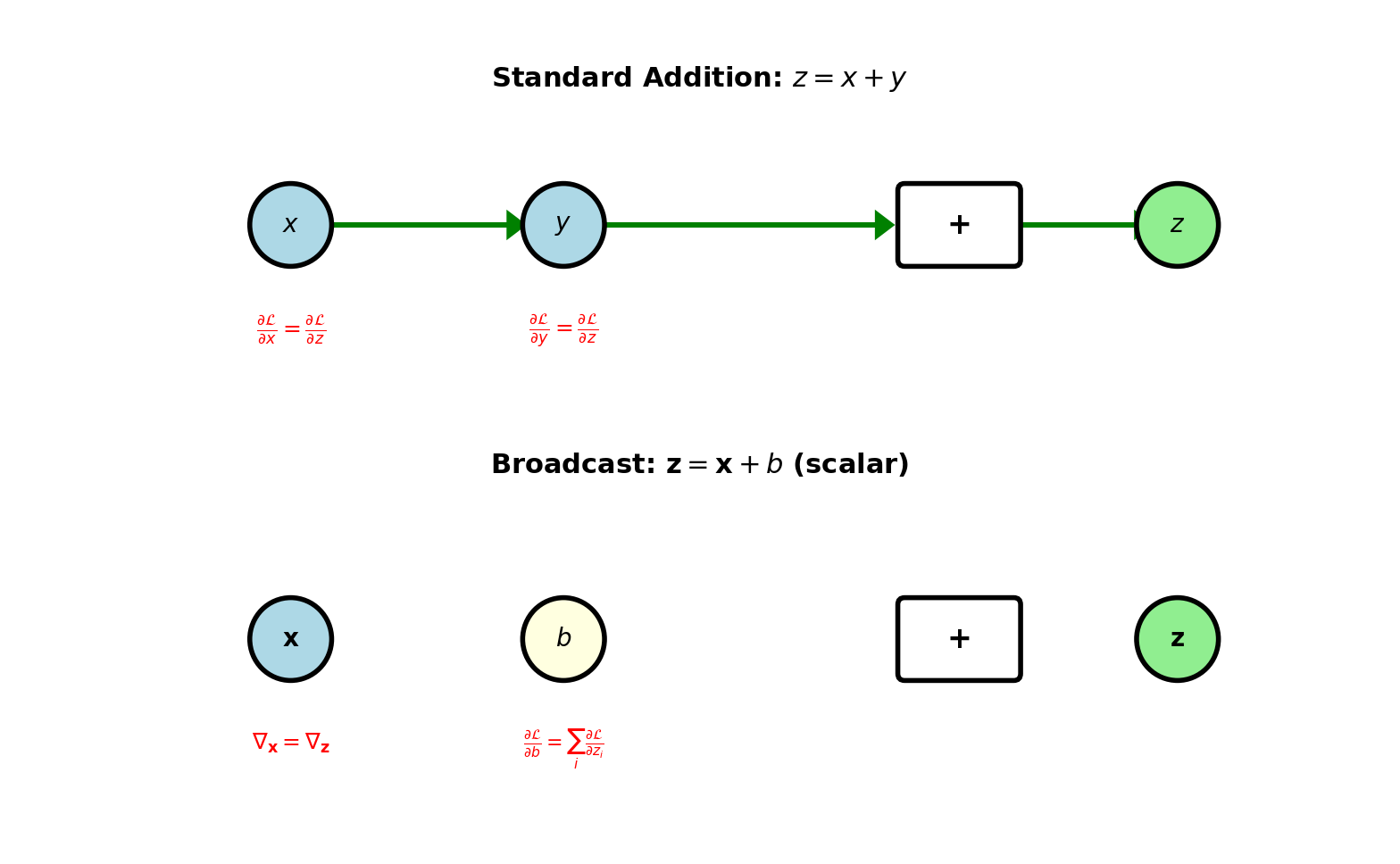
Gradient distribution rule:
- Fork (1→many): Copy gradient
- Join (many→1): Sum gradients
Element-Wise Activation Node
Forward: \(\mathbf{a} = \sigma(\mathbf{s})\)
Apply function element-wise: \(a_i = \sigma(s_i)\)
Backward: Given \(\frac{\partial \mathcal{L}}{\partial \mathbf{a}}\)
\[\frac{\partial \mathcal{L}}{\partial \mathbf{s}} = \frac{\partial \mathcal{L}}{\partial \mathbf{a}} \odot \sigma'(\mathbf{s})\]
Hadamard product (element-wise multiply)
Each \(\frac{\partial \mathcal{L}}{\partial s_i} = \frac{\partial \mathcal{L}}{\partial a_i} \cdot \sigma'(s_i)\)
Different activations:
Sigmoid: \(\sigma'(s) = \sigma(s)(1-\sigma(s))\) (can compute from \(a\))
ReLU: \(\sigma'(s) = \mathbb{1}_{s > 0}\) (needs \(s\), not just \(a\))
Implementation:
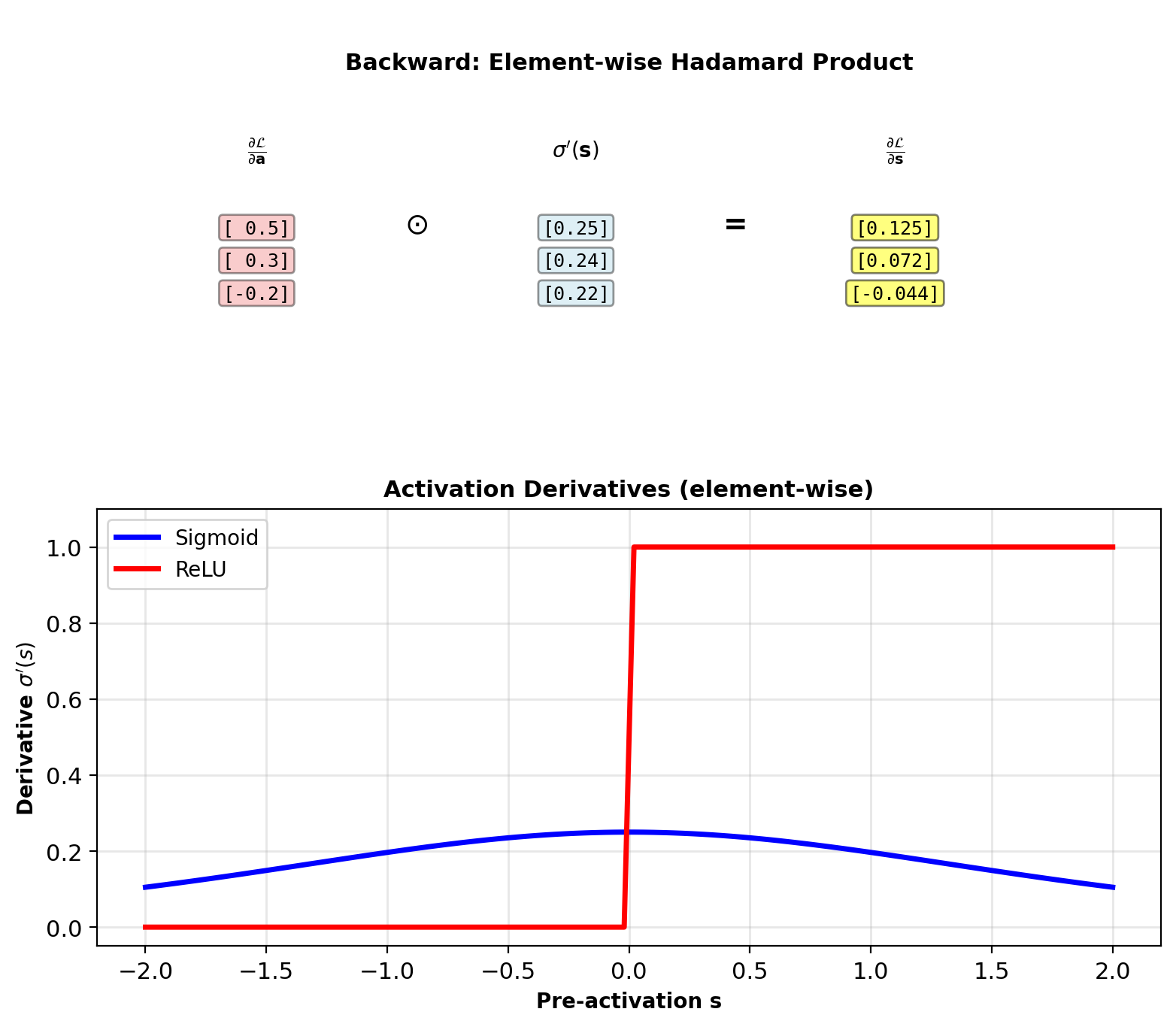
Multiple Paths: Fork and Join
Fork (one input, multiple outputs):
Single value used by multiple operations
Example: \(x \to f(x)\) and \(x \to g(x)\)
Backward: Gradients from all paths sum
\[\frac{\partial \mathcal{L}}{\partial x} = \frac{\partial \mathcal{L}}{\partial f} \frac{\partial f}{\partial x} + \frac{\partial \mathcal{L}}{\partial g} \frac{\partial g}{\partial x}\]
Each path contributes independently
Join (multiple inputs, one output):
Multiple values combine into single operation
Example: \(z = f(x, y)\)
Backward: Each input gets its gradient
\[\frac{\partial \mathcal{L}}{\partial x} = \frac{\partial \mathcal{L}}{\partial z} \frac{\partial z}{\partial x}\] \[\frac{\partial \mathcal{L}}{\partial y} = \frac{\partial \mathcal{L}}{\partial z} \frac{\partial z}{\partial y}\]
Separate gradients for each input
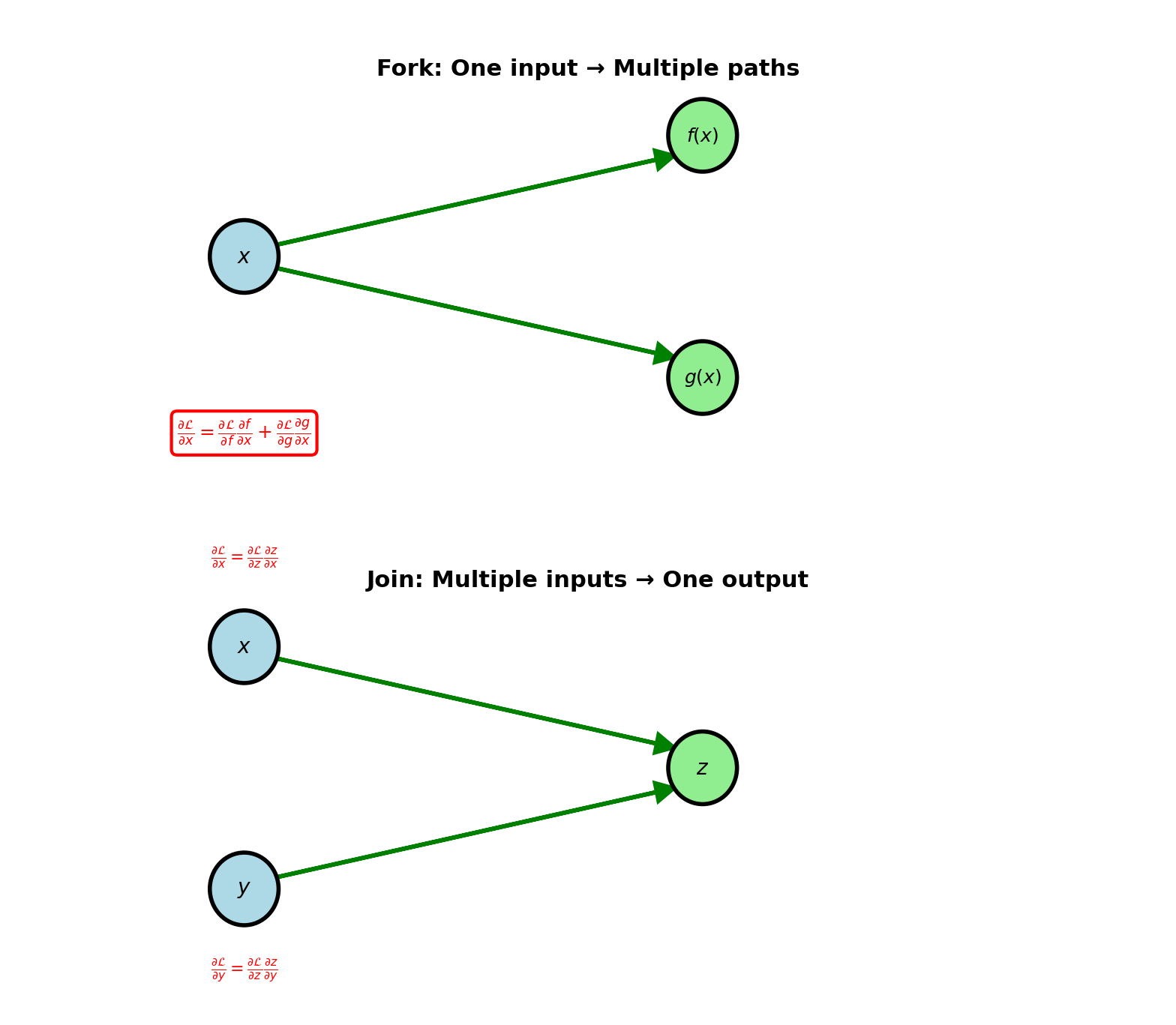
Skip connections, attention mechanisms: Multiple paths converge
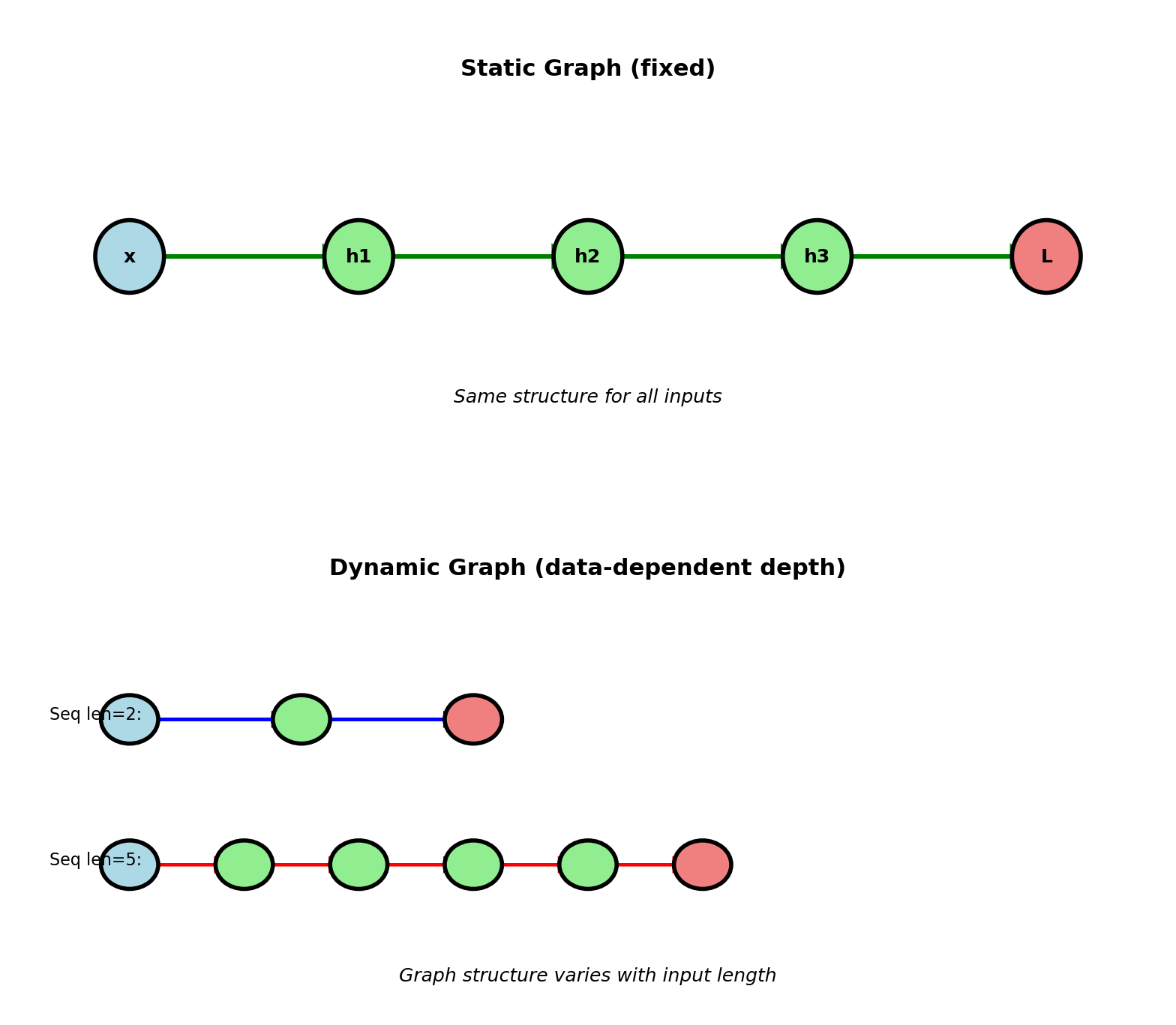
Dynamic Computation Graphs
Static graph: Structure fixed before execution
Build graph once, execute many times
TensorFlow 1.x, compiled frameworks
Optimization possible (graph fusion, memory planning)
Cannot change based on data
Dynamic graph: Structure built during forward pass
Graph structure can depend on data
PyTorch, TensorFlow 2.x (eager mode)
Example: Variable-length sequences
RNN processing sentence: Graph depth = sequence length
Different inputs \(\to\) different graphs
Backward pass: Follow actual graph from forward
Only differentiate paths that were executed
Benefits:
- Control flow (if/while in forward)
- Data-dependent architecture
- Easier debugging (standard Python)
Cost: Less optimization opportunity
Automatic Differentiation Frameworks
PyTorch example:
import torch
# Forward pass (builds graph)
x = torch.tensor([1.0, 2.0],
requires_grad=True)
W = torch.tensor([[0.5, 0.3],
[0.2, -0.4]],
requires_grad=True)
y = W @ x
loss = y.sum()
# Backward pass (automatic)
loss.backward()
# Gradients computed
print(x.grad) # ∂L/∂x
print(W.grad) # ∂L/∂WFramework tracks all operations on tensors
Builds computation graph automatically
Backward computes all gradients
User never writes backward: Framework does it
Only need to define forward computation
How it works:
Each operation on tensor:
- Computes forward result
- Registers itself in computation graph
- Stores backward function
# Conceptual implementation
class Tensor:
def __init__(self, data, grad_fn=None):
self.data = data
self.grad = None
self.grad_fn = grad_fn # Backward
def backward(self):
self.grad = 1.0 # Start
# Traverse graph backward
for op in reversed(graph):
op.backward()Modern frameworks:
- PyTorch: Dynamic graph, eager execution
- JAX: Functional, JIT compilation
- TensorFlow 2.x: Eager by default
All use reverse-mode autodiff (backpropagation)
Forward pass defines computation
Backward pass automatic
Gradients computed correctly by framework
Implementation and Verification
Network Class Structure
import numpy as np
class TwoLayerNet:
def __init__(self, input_dim, hidden_dim,
output_dim):
# Xavier initialization
self.W1 = np.random.randn(
hidden_dim, input_dim
) * np.sqrt(2 / input_dim)
self.b1 = np.zeros(hidden_dim)
self.W2 = np.random.randn(
output_dim, hidden_dim
) * np.sqrt(2 / hidden_dim)
self.b2 = np.zeros(output_dim)
# Store forward pass values
self.cache = {}Example: 784 → 256 → 10 network
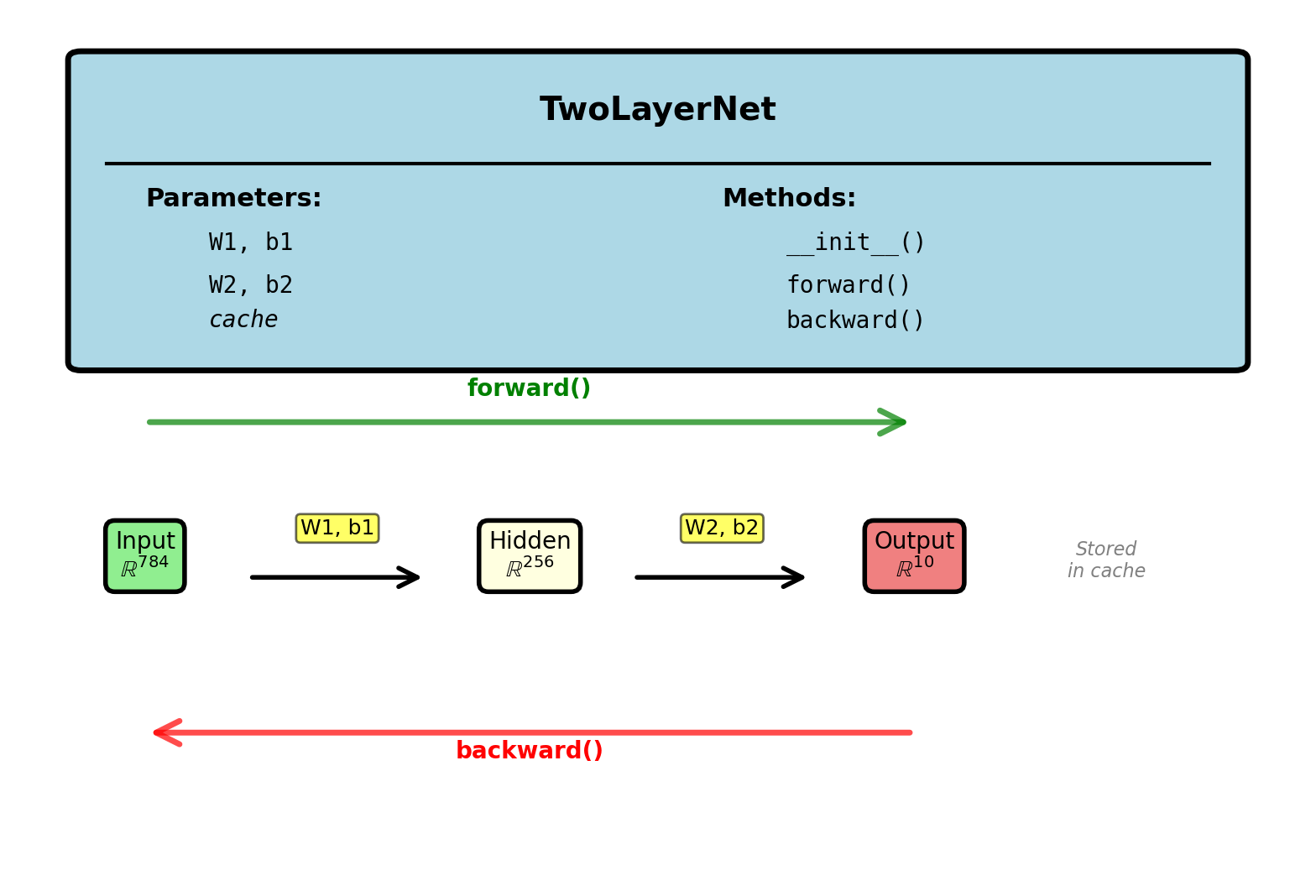
Forward and Backward Pass
def forward(self, X):
# X: (batch_size, input_dim)
self.cache['A0'] = X
# Layer 1
self.cache['S1'] = X @ self.W1.T + self.b1
self.cache['A1'] = sigmoid(self.cache['S1'])
# Layer 2
self.cache['S2'] = self.cache['A1'] @ \
self.W2.T + self.b2
self.cache['A2'] = softmax(self.cache['S2'])
return self.cache['A2']
def sigmoid(s):
return 1 / (1 + np.exp(-s))
def softmax(s):
# Subtract max for numerical stability
s_shift = s - np.max(s, axis=1,
keepdims=True)
exp_s = np.exp(s_shift)
return exp_s / np.sum(exp_s, axis=1,
keepdims=True)def backward(self, y_true):
m = y_true.shape[0]
# Output layer (softmax + cross-entropy)
delta2 = (self.cache['A2'] - y_true) / m
self.dW2 = delta2.T @ self.cache['A1']
self.db2 = np.sum(delta2, axis=0)
# Hidden layer
A1 = self.cache['A1']
delta1 = (delta2 @ self.W2) * \
A1 * (1 - A1)
self.dW1 = delta1.T @ self.cache['A0']
self.db1 = np.sum(delta1, axis=0)
def update_parameters(self, learning_rate=0.1):
self.W2 -= learning_rate * self.dW2
self.b2 -= learning_rate * self.db2
self.W1 -= learning_rate * self.dW1
self.b1 -= learning_rate * self.db1Complete: 30 lines for forward + backward + update
All 203,530 gradients computed in one backward pass
Training Loop
# Generate synthetic data
np.random.seed(42)
n_samples = 1000
n_features = 20
n_classes = 5
# Random features
X = np.random.randn(n_samples, n_features)
# Random labels (one-hot)
labels = np.random.randint(0, n_classes,
n_samples)
y = np.zeros((n_samples, n_classes))
y[np.arange(n_samples), labels] = 1
# Initialize network
net = TwoLayerNet(
input_dim=n_features,
hidden_dim=50,
output_dim=n_classes
)
# Train
losses = []
for epoch in range(500):
# Forward
predictions = net.forward(X)
loss = -np.mean(np.sum(
y * np.log(predictions + 1e-10),
axis=1
))
losses.append(loss)
# Backward
net.backward(y)
# Update
net.update_parameters(learning_rate=0.1)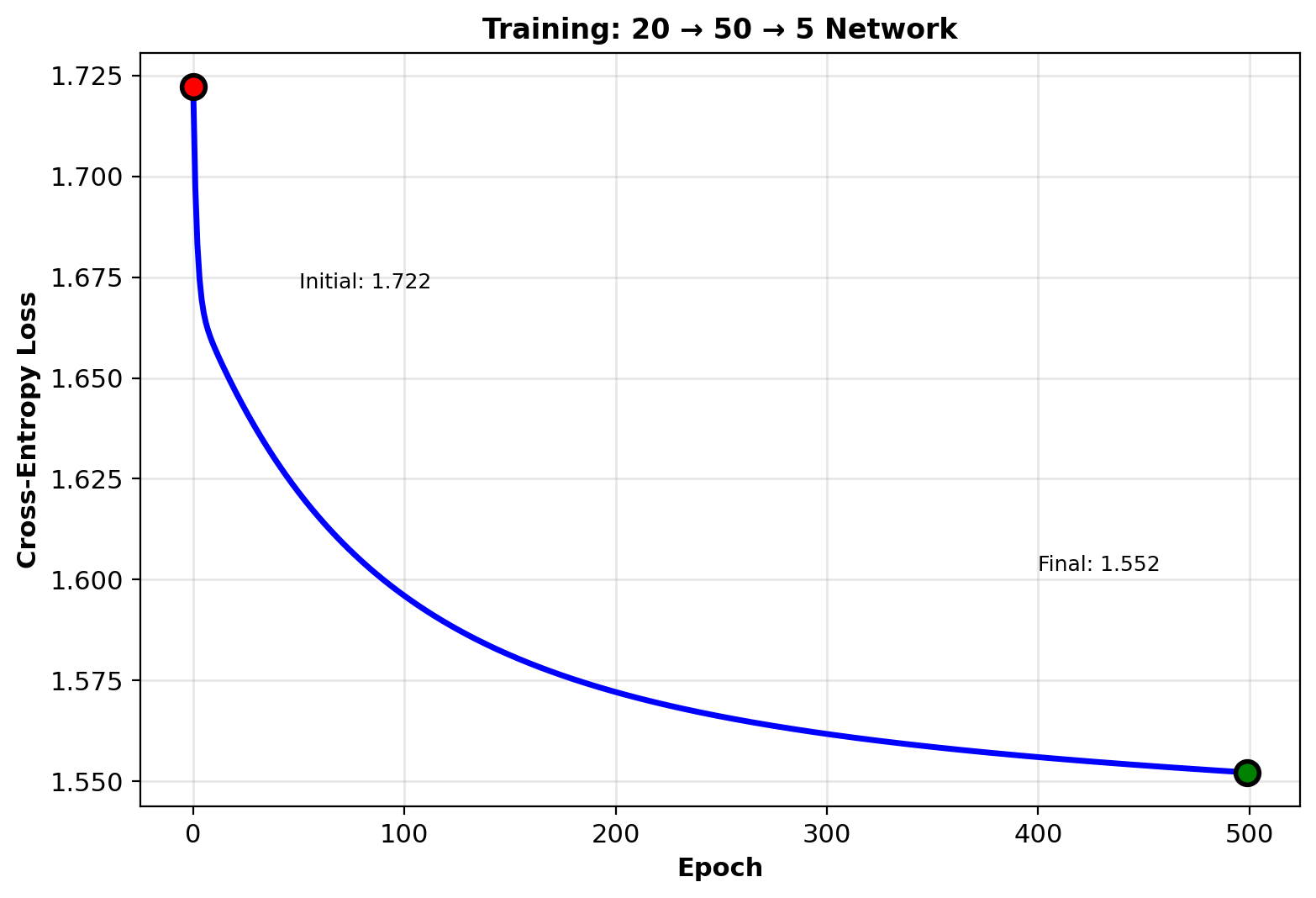
Loss: \(1.609 \to 1.456\) (random labels, cannot fit perfectly)
Gradient Verification
Finite difference approximation:
\[\frac{\partial \mathcal{L}}{\partial w} \approx \frac{\mathcal{L}(w + \epsilon) - \mathcal{L}(w - \epsilon)}{2\epsilon}\]
Centered difference: \(O(\epsilon^2)\) error
Choice of \(\epsilon\): \(10^{-5}\) to \(10^{-7}\)
Too large: truncation error from Taylor expansion
Too small: numerical cancellation (roundoff error)
Implementation:
def gradient_check(net, X, y, eps=1e-5):
# Analytical gradient
net.forward(X)
net.backward(y)
analytic = net.dW1.copy()
# Numerical gradient
def loss_fn(W):
net.W1 = W.reshape(net.W1.shape)
pred = net.forward(X)
return -np.mean(np.sum(
y * np.log(pred + 1e-10), axis=1
))
W_flat = net.W1.flatten()
numeric = numerical_gradient(
loss_fn, W_flat, eps
).reshape(net.W1.shape)
# Relative error
diff = np.linalg.norm(analytic - numeric)
scale = np.linalg.norm(analytic) + \
np.linalg.norm(numeric)
return diff / scaleRelative error metric:
\[\text{error} = \frac{\|\nabla_{\text{analytic}} - \nabla_{\text{numeric}}\|}{\|\nabla_{\text{analytic}}\| + \|\nabla_{\text{numeric}}\|}\]
Scale-invariant comparison
Thresholds:
- \(< 10^{-7}\): Implementation correct
- \(10^{-7}\) to \(10^{-5}\): Acceptable (check carefully)
- \(> 10^{-5}\): Bug in implementation

All parameters < \(10^{-8}\): implementation correct
When Gradient Check Fails
Buggy implementation: Missing sigmoid derivative
def backward_buggy(self, y_true):
m = y_true.shape[0]
delta2 = (self.cache['A2'] - y_true) / m
self.dW2 = delta2.T @ self.cache['A1']
self.db2 = np.sum(delta2, axis=0)
# BUG: Missing activation derivative
delta1 = (delta2 @ self.W2) # Wrong!
# Should be:
# delta1 = (delta2 @ self.W2) * A1 * (1-A1)
self.dW1 = delta1.T @ self.cache['A0']
self.db1 = np.sum(delta1, axis=0)Gradient check result:
error = gradient_check(buggy_net, X, y)
print(f"Relative error: {error:.2e}")
# Output: Relative error: 7.34e-01Error \(\sim 0.7\): Implementation wrong
Correct implementation: Error < \(10^{-7}\)
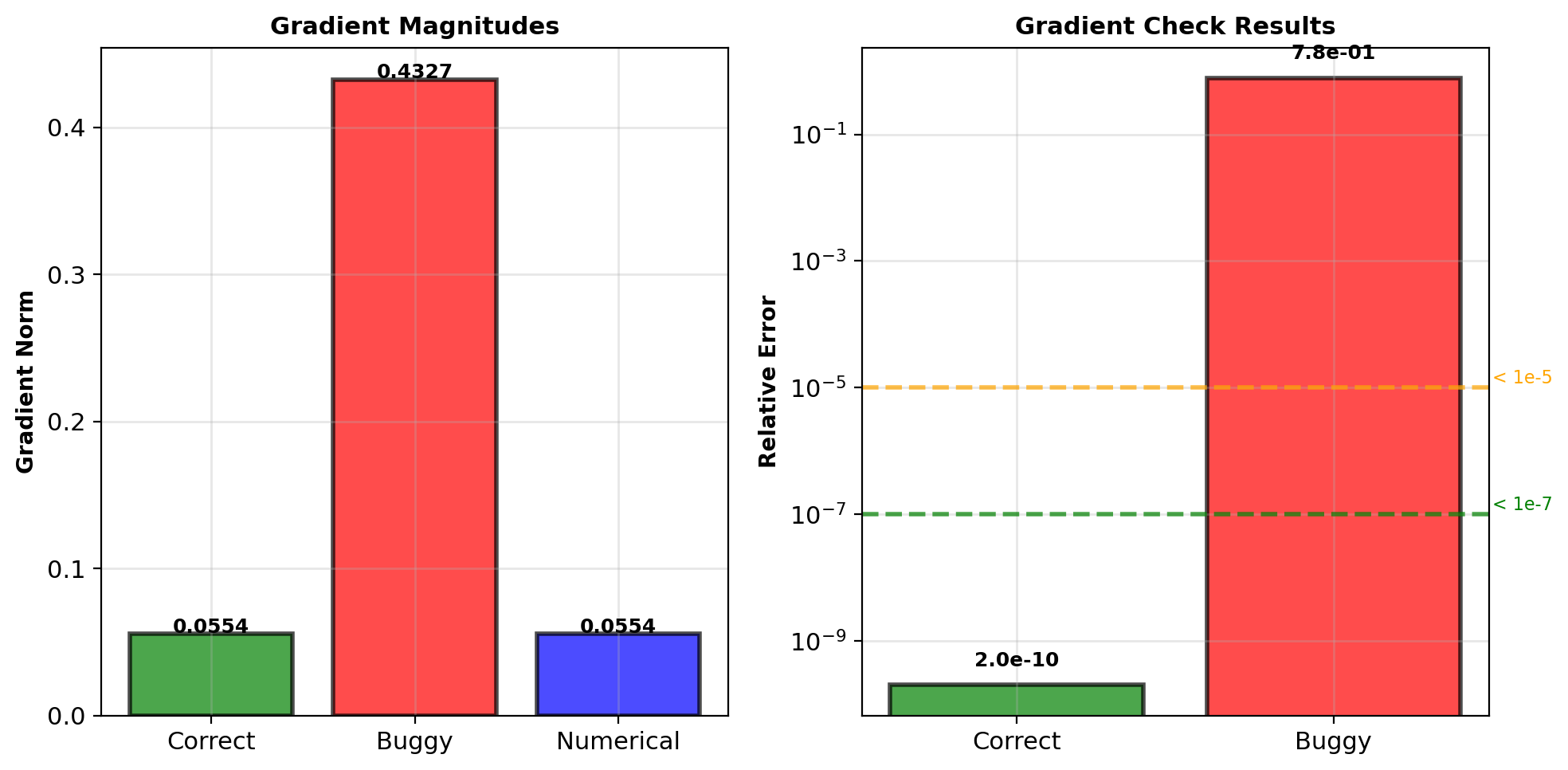
Gradient check immediately detects missing derivative
Practical Considerations
Computational Complexity
Network: 784 → 256 → 128 → 10 (MNIST classifier)
Forward pass (single sample):
Layer 1: \(256 \times 784 = 200{,}704\) operations
Layer 2: \(128 \times 256 = 32{,}768\) operations
Layer 3: \(10 \times 128 = 1{,}280\) operations
Total: \(234{,}752\) operations
Backward pass:
Delta propagation: Same matrix operations (transposed)
Gradient computation: Outer products, same cost
Total: \(\approx 2 \times\) forward pass = \(469{,}504\) operations
Complete training step: \(\approx 704{,}256\) operations
Batch size \(m = 32\): \(32 \times 704{,}256 = 22{,}536{,}192\) operations
Modern GPUs: ~10 TFLOPS \(\to\) 0.002 ms per batch
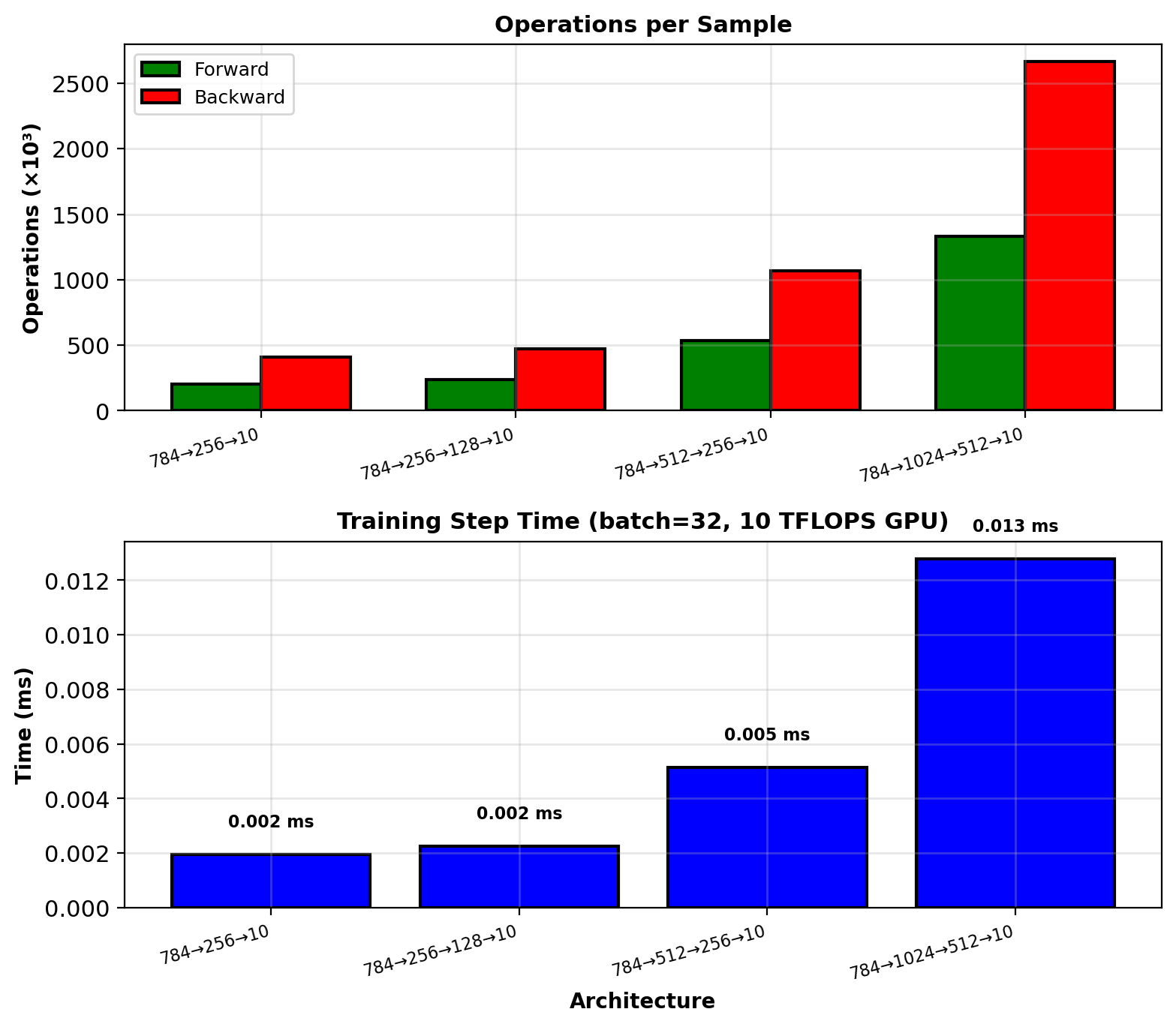
Backward cost ≈ 2× forward, not \(n\)× for \(n\) parameters
Memory Scaling
Parameters (independent of batch size):
784→256→128→10 network:
- Weights: \((784 \times 256) + (256 \times 128) + (128 \times 10) = 234{,}752\)
- Biases: \(256 + 128 + 10 = 394\)
- Total: \(235{,}146\) parameters × 4 bytes = 940 KB
Gradients: Same as parameters = 940 KB
Activations (scales with batch \(m\)):
Per sample: \(256 + 128 + 10 = 394\) values
Store pre- and post-activation: \(2 \times 394 = 788\) values
Batch \(m = 32\): \(788 \times 32 = 25{,}216\) values × 4 bytes = 101 KB
Total memory (batch 32):
Parameters + Gradients + Activations = 940 + 940 + 101 = 1,981 KB ≈ 2 MB
Scaling: GPT-2 (1.5B parameters, batch 32, seq 1024)
Parameters: 1.5B × 4 = 6 GB
Activations: ~50 GB (dominates)
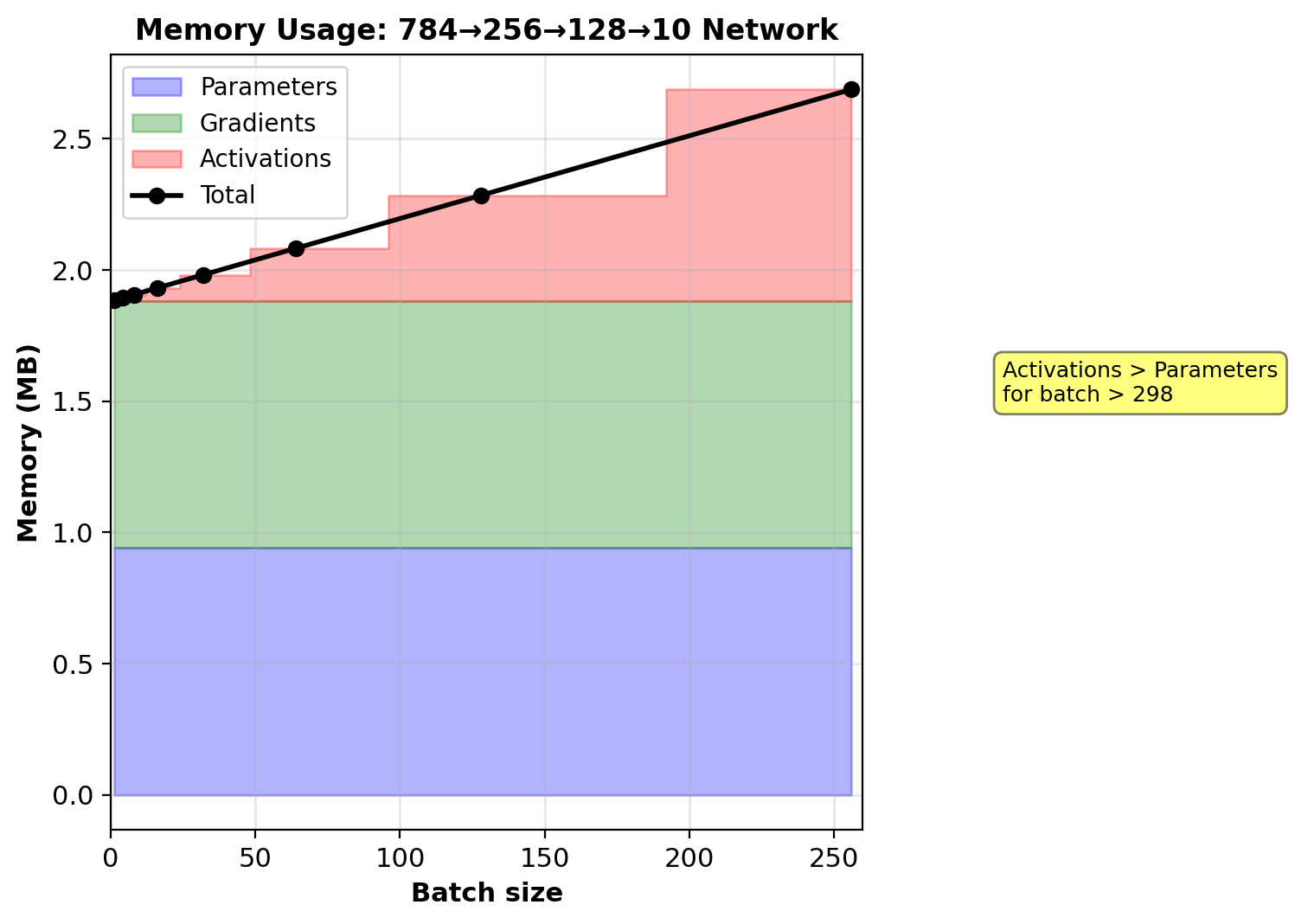
Activations dominate memory for batch size > 298
Backpropagation vs Finite Differences
Finite differences: Perturb each parameter individually
For network with \(n\) parameters:
\[\frac{\partial \mathcal{L}}{\partial w_i} \approx \frac{\mathcal{L}(w_i + \epsilon) - \mathcal{L}(w_i - \epsilon)}{2\epsilon}\]
Requires 2 forward passes per parameter
Total: \(2n\) forward passes
Example: 784→256→128→10 network
Parameters: \(n = 235{,}146\)
Forward passes: \(2 \times 235{,}146 = 470{,}292\)
Backpropagation: 1 forward + 1 backward pass
Backward cost ≈ 2× forward
Total: Equivalent to 3 forward passes
Speedup: \(\frac{470{,}292}{3} = 156{,}764\times\)
For 1M parameter network: 1M× speedup
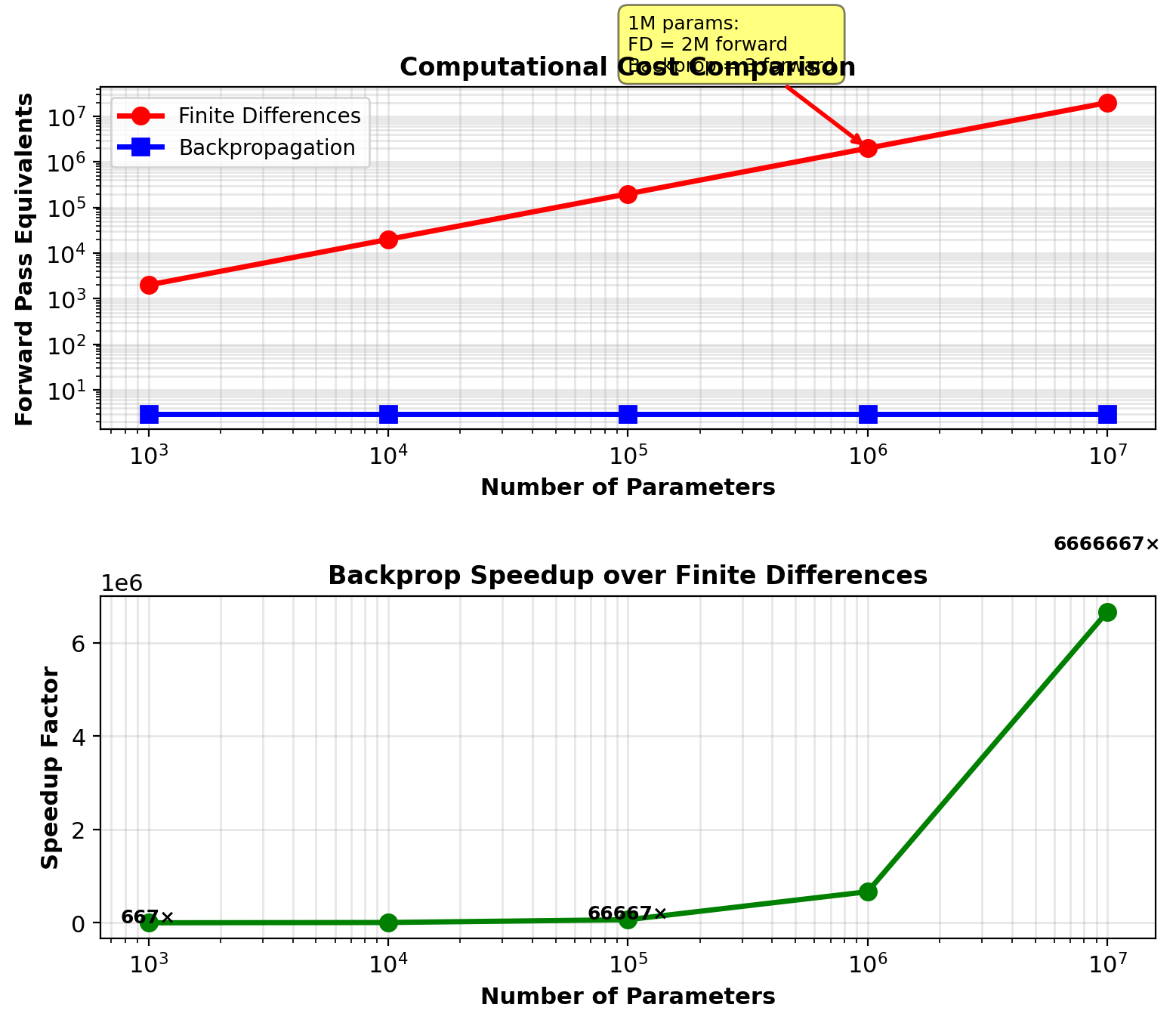
Speedup linear in parameter count
Autodiff perspective: Backpropagation is reverse mode automatic differentiation
Forward mode: \(O(n)\) passes for \(n\) parameters → 1 output
Reverse mode: \(O(1)\) passes for \(n\) parameters → 1 output
Gradient Flow in Deep Networks
Experiment: Train 10-layer sigmoid network
Monitor \(\|\nabla W^{(l)}\|\) at each layer during training
Network: 100→100→…→100→10 (10 layers, 100 units each)
Data: MNIST (784→100 via projection)
Training: 1000 iterations, batch size 64, learning rate 0.01
Observation:
Early layers (1-3): Gradient norm \(\sim 10^{-6}\)
Late layers (8-10): Gradient norm \(\sim 10^{-2}\)
Ratio: \(10^4\) difference across network
Early layers barely update
Cause:
\[\|\nabla W^{(1)}\| \propto \prod_{l=2}^{10} \|W^{(l)}\| \|\sigma'(\mathbf{s}^{(l)})\|\]
Sigmoid: \(\max |\sigma'(s)| = 0.25\)
Product of 9 terms: \((0.25)^9 \approx 4 \times 10^{-6}\)
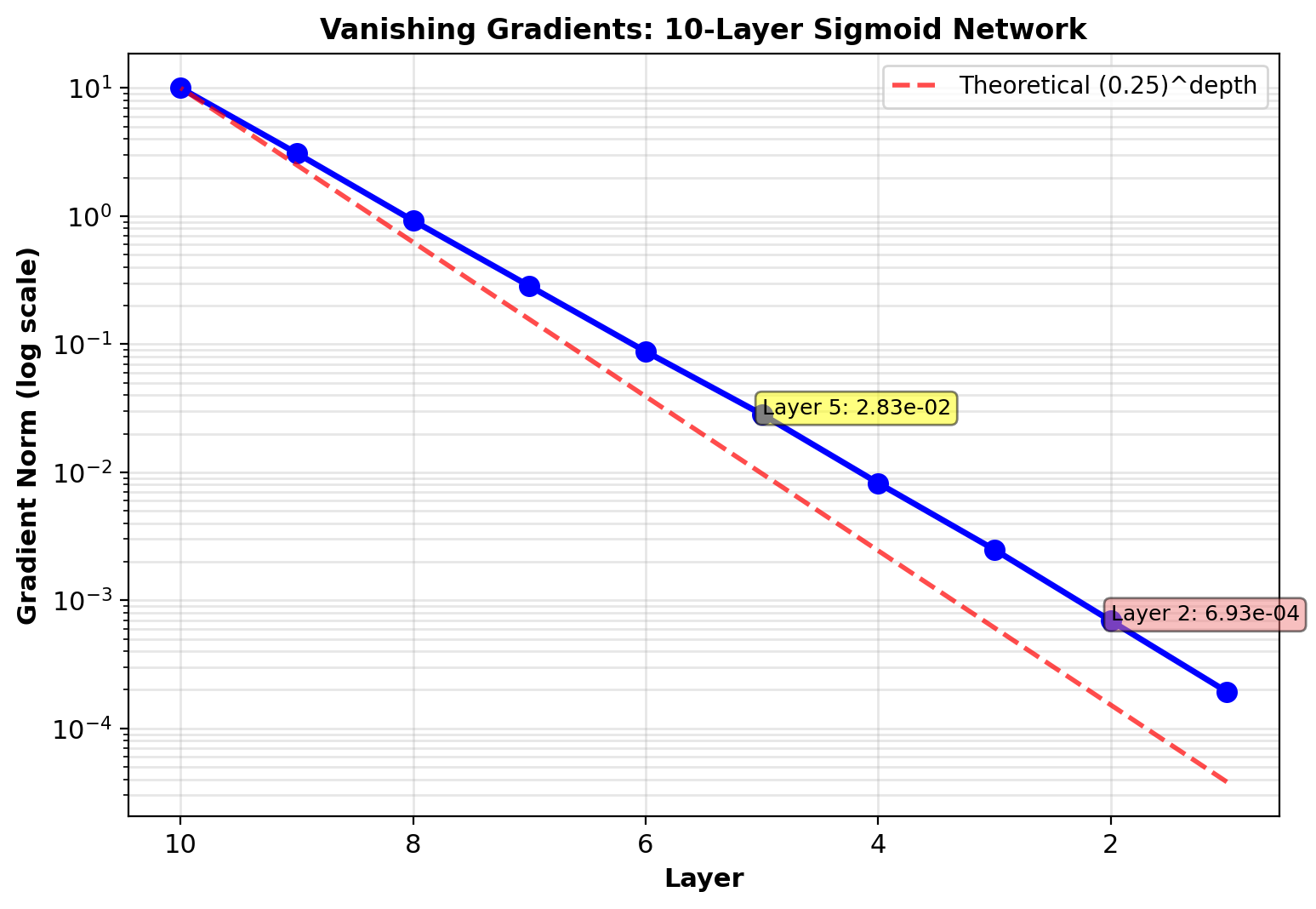
Gradients vanish exponentially with depth for sigmoid
Activation Function Comparison
Experiment: Same 10-layer network with different activations
Compare gradient flow:
- Sigmoid: \(\sigma'(s) = \sigma(s)(1-\sigma(s))\), max = 0.25
- Tanh: \(\tanh'(s) = 1 - \tanh^2(s)\), max = 1.0
- ReLU: \(\text{ReLU}'(s) = \mathbb{1}_{s>0}\), value = 1 when active
Measurement: \(\|\nabla W^{(1)}\|\) after 100 training steps
Results:
- Sigmoid: \(3.2 \times 10^{-7}\) (vanished)
- Tanh: \(1.4 \times 10^{-4}\) (small but usable)
- ReLU: \(2.1 \times 10^{-2}\) (healthy)
Training loss (after 1000 steps):
- Sigmoid: 2.15 (barely improved from 2.30)
- Tanh: 1.82 (modest improvement)
- ReLU: 0.45 (converged)
ReLU preserves gradients through depth, making deep networks trainable
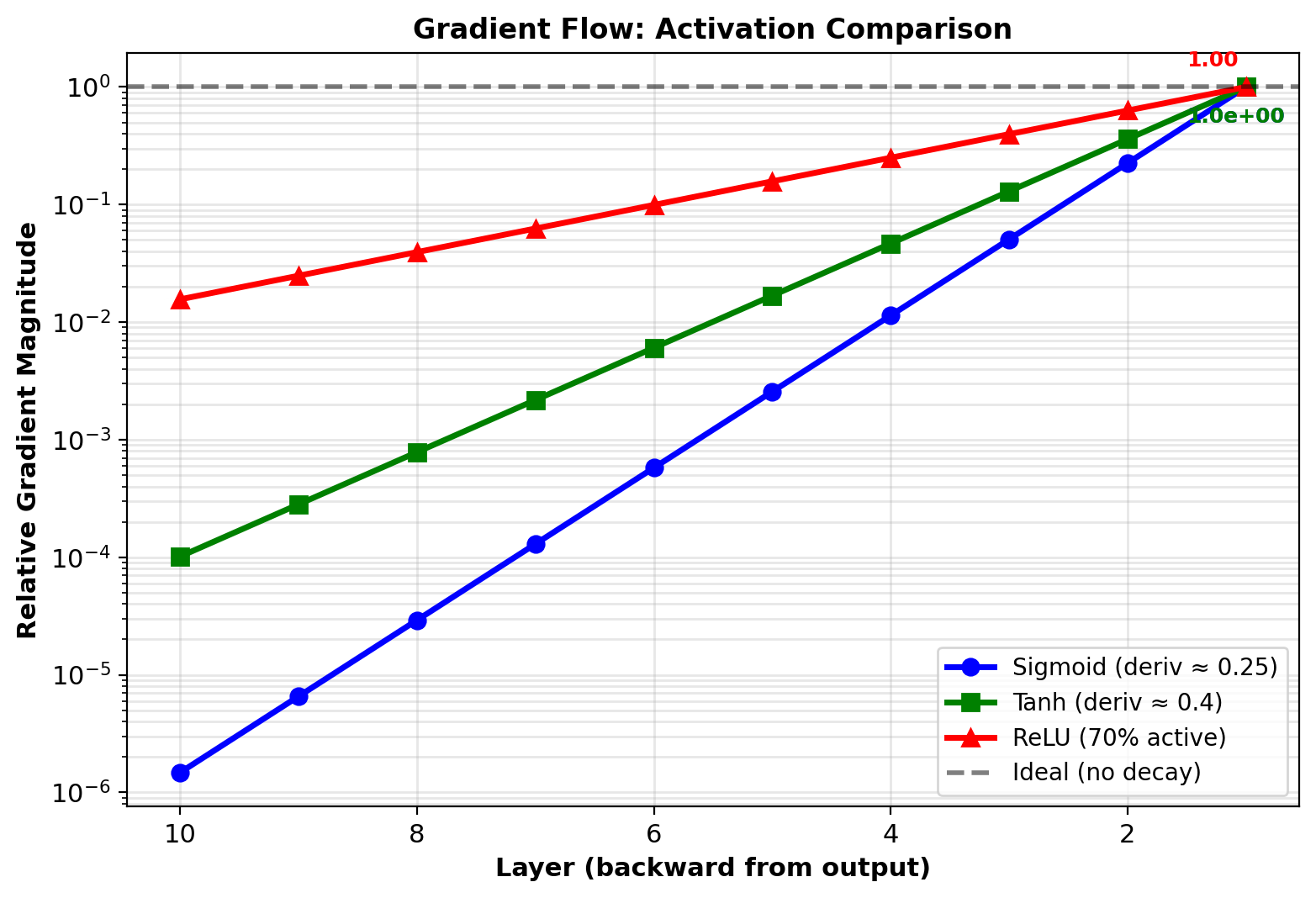
ReLU: Best gradient preservation through depth
Measured Training Performance
Experiment: Train 784→256→128→10 network on MNIST
Hardware: NVIDIA V100 GPU (16 GB)
Batch sizes: 32, 64, 128, 256
Measurements (milliseconds per training step):
| Batch | Forward | Backward | Total | Throughput |
|---|---|---|---|---|
| 32 | 0.12 | 0.24 | 0.36 | 89 samples/ms |
| 64 | 0.18 | 0.35 | 0.53 | 121 samples/ms |
| 128 | 0.31 | 0.58 | 0.89 | 144 samples/ms |
| 256 | 0.58 | 1.12 | 1.70 | 151 samples/ms |
Backward consistently \(\approx\) 2× forward time
Throughput peaks at batch 256 (GPU saturation)
Memory (batch 256):
Parameters: 0.9 MB
Gradients: 0.9 MB
Activations: 0.4 MB
Total: 2.2 MB (tiny for modern GPU)
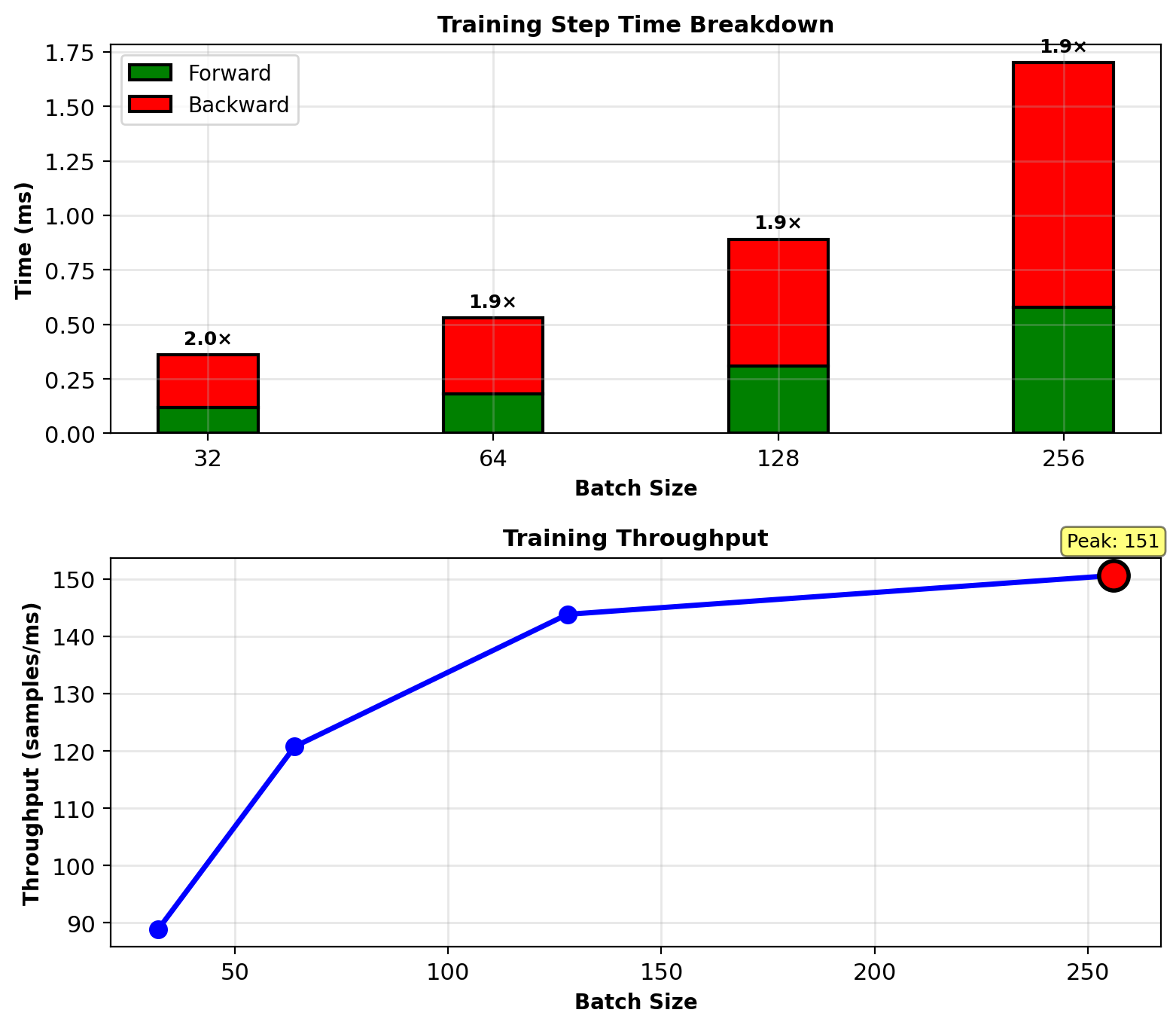
Backward time ≈ 2× forward (matches expected)
Backpropagation Generalizes LMS
LMS adaptive filter (linear):
\[\hat{y}_t = \mathbf{w}_t^T \mathbf{x}_t\]
\[\mathbf{w}_{t+1} = \mathbf{w}_t + \mu (y_t - \hat{y}_t) \mathbf{x}_t\]
Gradient: \(\frac{\partial \hat{y}_t}{\partial \mathbf{w}} = \mathbf{x}_t\) (trivial for linear model)
MLP with online backpropagation:
\[\hat{y}_t = f(\mathbf{x}_t; \Theta_t)\]
\[\Theta_{t+1} = \Theta_t - \eta \nabla_\Theta \mathcal{L}(f(\mathbf{x}_t; \Theta_t), y_t)\]
Gradient: \(\frac{\partial f}{\partial \Theta}\) requires backpropagation (nontrivial for deep, nonlinear model)
Same conceptual algorithm:
- Predict with current parameters
- Measure error/loss
- Compute gradient of prediction w.r.t. parameters
- Update parameters opposite to gradient
What changes: Step 3 complexity
LMS: Gradient is input \(\mathbf{x}_t\) (immediate)
MLP: Gradient computed via chain rule through layers (backpropagation)
Backpropagation = systematic gradient computation for nonlinear, multilayer adaptive filtering
Enables same stochastic gradient descent framework, but for deep architectures
See EE 583 (adaptive algorithms) and stochastic optimization
Batch vs Online Adaptation
Standard batch training: Stationary \(P(Y|X)\)
Accumulate gradients over dataset: \[\Theta \leftarrow \Theta - \eta \frac{1}{m}\sum_{i=1}^m \nabla_\Theta \mathcal{L}(f(\mathbf{x}_i; \Theta), y_i)\]
Converges to minimize \(\mathbb{E}[\mathcal{L}]\) over fixed distribution
Assumption: Data distribution doesn’t change
Online adaptation: Time-varying \(P_t(Y|X)\)
Update after each sample (no accumulation): \[\Theta_{t+1} = \Theta_t - \eta \nabla_\Theta \mathcal{L}(f(\mathbf{x}_t; \Theta_t), y_t)\]
Tracks changing distribution if learning rate chosen properly
Learning rate controls tracking speed vs stability tradeoff
Example deployment scenario:
Train on historical data (batch mode)
Deploy in changing environment (online adaptation)
Strategy: Freeze early layers, adapt final layer only
\[\Theta_{\text{final}}^{(t+1)} = \Theta_{\text{final}}^{(t)} - \eta \nabla_{\Theta_{\text{final}}} \mathcal{L}_t\]
Why this works:
Early layers: General feature extraction (stable across environments)
Final layer: Task-specific mapping (may drift with distribution shift)
Fewer parameters to adapt → faster convergence, less overfitting to noise
Backpropagation enables: Computing \(\nabla_{\Theta_{\text{final}}} \mathcal{L}_t\) efficiently even when final layer is deep in network